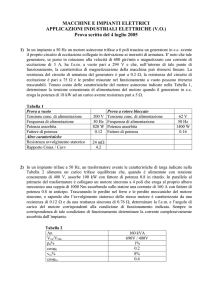
Il comportamento del motore asincrono è descritto da un sistema di
equazioni non lineari; non è, quindi, possibile, quando si desidera
ricavare dei legami funzionali, determinare delle funzioni di
trasferimento relative alle piene escursioni delle variabili, ma
occorre limitarsi a considerare funzioni di trasferimento relative a
piccole variazioni attorno a un punto di lavoro (linearizzazione).
La linearizzazione è, però, facilitata dalla constatazione che il valore
medio della coppia motrice è influenzato solo dalla prima armonica
della tensione (o corrente) di alimentazione;
è, pertanto, possibile considerare una alimentazione sinusoidale
scegliendo assi di riferimento d e q rotanti con una velocità
angolare pari alla pulsazione istantanea della tensione (o della
corrente) di alimentazione.
La tecnica di controllo impiegata per l’azionamento può prevedere
che l’algoritmo di controllo determini:
- il modulo e la frequenza della tensione da applicare
all’avvolgimento di statore del motore, che risulta, quindi,
alimentato a tensione impressa;
- il modulo e la direzione del vettore di corrente da applicare
all’avvolgimento di statore del motore.
Nel secondo caso l’alimentazione del motore può venire effettuata
impiegando un convertitore a corrente impressa oppure un
convertitore a tensione impressa con opportuni anelli di controllo
atti ad imporre la corrente desiderata.
Quando si impiega un convertitore a corrente impressa
l’alimentazione del motore, risulta, ovviamente, effettuata in
corrente; anche quando si utilizza un convertitore a tensione
impressa, se gli anelli di controllo della corrente sono
sufficientemente veloci, è possibile supporre che la corrente
applicata al motore coincida con il valore desiderato e, quindi,
approssimare il comportamento del motore a quello corrispondente
ad una alimentazione in corrente.
Approccio classico:
alimentazione in
tensione
oppure
Controllo vettoriale:
alimentazione in
corrente
Quando la macchina asincrona è alimentata a tensione impressa è
conveniente scegliere gli assi di riferimento d e q rotanti con una
velocità angolare pari alla pulsazione istantanea wa della
tensione di alimentazione e orientati in modo tale che risulti
vsd = vs e vsq = 0, essendo vs il modulo del vettore rappresentativo
dell’armonica fondamentale della tensione di alimentazione.
Con tale scelta, assumendo come variabili di stato le componenti dei
flussi di statore e di rotore, il modello del motore può essere riscritto
nella seguente forma matriciale:
essendo:
E’ possibile effettuare una linearizzazione del modello prendendo
in considerazione il vettore delle variazioni delle componenti dei
flussi di statore e di rotore attorno al punto di lavoro, cioè:
in cui il pedice o caratterizza il valore assunto dalle grandezze nel
punto di lavoro prescelto.
Effettuando la linearizzazione si ottiene:
essendo
Se si considerano, quindi, le trasformate di Laplace delle variazioni
dei flussi, del modulo della tensione, della pulsazione di
alimentazione e della velocità angolare, si ottiene:
essendo s la variabile di Laplace.
Analogamente, se si considera la variazione della coppia
elettromagnetica:
si ottiene:
essendo:
Trasformando secondo Laplace e sostituendo l’espressione della
variazione del flusso, si ottiene, infine, la seguente espressione per
la trasformata della variazione della coppia elettromagnetica:
che può essere riscritta nella forma:
essendo:
Schema a blocchi funzionale del modello linearizzato.
Il modello linearizzato consente di valutare il comportamento
dinamico del motore asincrono alimentato a tensione impressa
nell’intorno di un generico punto di lavoro e può essere impiegato
per:
* verificare la stabilità del motore;
* effettuare una sintesi di primo tentativo del dispositivo di controllo.
Il calcolo delle espressioni delle funzioni di trasferimento risulta
alquanto laborioso e poco significativo, a causa dell’elevata
complessità delle equazioni e della forte dipendenza dal punto di
lavoro.
E’, però, possibile, quando la pulsazione di alimentazione è
sufficientemente elevata, impiegare delle espressioni semplificate
G1’, G2’, e G3’ delle funzioni di trasferimento.
In appendice è riportato un approccio che consente di ricavare delle
espressioni approssimate G1’, G2’, e G3’ delle tre funzioni di
trasferimento E’ interessante notare che le tre funzioni di
trasferimento approssimate sono legate tra loro dalla seguente
relazione:
Quando un motore asincrono è alimentato a tensione
impressa, si possono verificare nella macchina fenomeni di
instabilità, anche per valori della pulsazione di scorrimento
minori di quella corrispondente alla coppia di rovesciamento.
Lo studio della stabilità può venire effettuato impiegando il
modello linearizzato; però, siccome l’instabilità si manifesta per
frequenze abbastanza basse non è possibile impiegare le
espressioni approssimate delle funzioni di trasferimento.
Una esauriente trattazione è riportata nel testo.
Schema a blocchi funzionale del modello linearizzato.
Luogo delle radici al variare di Vs
Per ricavare il modello linearizzato del motore
asincrono con alimentazione a corrente impressa, è
conveniente prendere in considerazione il modello del
motore che utilizza, come variabili di stato, le
componenti della corrente di statore e quelle del flusso
di rotore.
Riscrivendo, con un diverso ordine dei termini che compaiono a
secondo membro, le ultime due equazioni del modello:
si ricava:
Si può constatare che gli andamenti delle componenti del flusso
rotorico dipendono solo da quelli delle componenti della corrente
statorica; pertanto il modello composto dalle precedenti due
equazioni è sufficiente a descrivere il comportamento del motore
asincrono con alimentazione a corrente impressa.
Come nel caso di alimentazione a tensione impressa, anche questo
modello è non lineare; per ricavare il modello linearizzato è ancora
conveniente scegliere gli assi di riferimento d e q rotanti con una
velocità angolare pari alla pulsazione istantanea della grandezza di
alimentazione, ma modificare l’orientamento in modo tale che risulti
isd = is e isq = 0.
Si ottiene:
in cui la pulsazione di scorrimento ws è pari alla
differenza wa - w.
Linearizzando tali equazioni attorno ad una condizione di equilibrio si
ottiene:
Nell’analisi a regime permanente si è visto che il vettore
rapprentativo della corrente è in anticipo rispetto a quello del
flusso di un angolo pari a:
Pertanto si ha:
essendo ro il modulo del flusso rotorico, a sua volta pari a:
Si ottiene, quindi:
Trasformando secondo Laplace le equazioni:
si ottiene:
e quindi:
essendo
Sostituendo, infine, le espressioni delle componenti del flusso, si
ricava:
Dall’espressione della coppia:
si ricava:
Trasformando secondo Laplace, si ottiene:
essendo:
E’ interessante osservare che nell’espressione della variazione della
coppia, non compare esplicitamente la velocità; pertanto, assumendo
la pulsazione di scorrimento come variabile di controllo e scegliendo
un modulo della corrente statorica direttamente dipendente dallo
scorrimento, non si ha alcuna reazione di velocità e, di conseguenza,
non si presentano fenomeni di instabilità.
E’, infine, conveniente ricavare le funzioni di trasferimento che
forniscono la dipendenza delle variazioni del modulo del flusso da
quelle del modulo della corrente e della pulsazione di scorrimento.
da
si ricava:
essendo: