Lezione 4

Energia Potenziale Elettrica
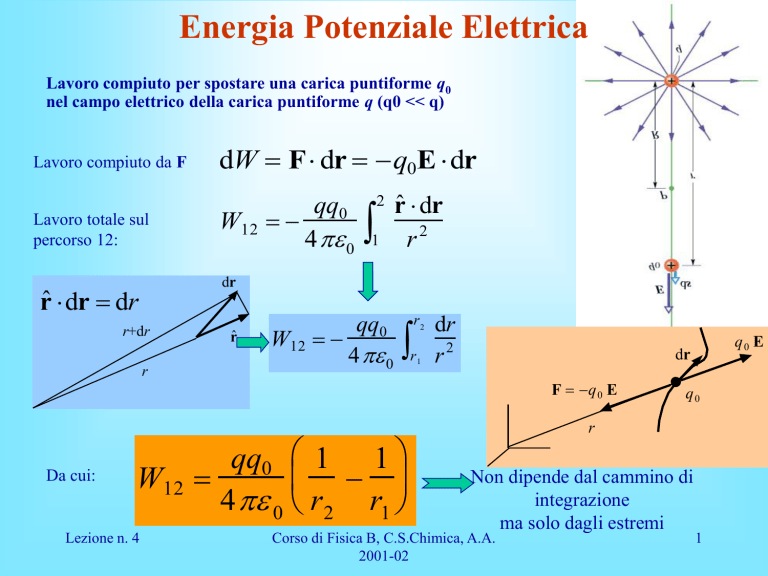
Lavoro compiuto per spostare una carica puntiforme q0
nel campo elettrico della carica puntiforme q (q0 << q)
Lavoro compiuto da F
Lavoro totale sul
percorso 12:
dW  F dr  q0E dr
W12
qq0

4  0

2
1
rˆ  dr
r2
dr
rˆ dr  dr
r+dr
r
r̂
W12
qq0

4  0

r2
r1
dr
r2
F  q 0 E
Da cui:
W12
Lezione n. 4
qq0  1 1 

  
4  0  r 2 r1 
q0 E
dr
q0
r
Non dipende dal cammino di
integrazione
ma solo dagli estremi
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
1
La forza elettrostatica è conservativa
W12  U2  U1
Unità di misura di U nel sistema SI: joule (J)
U2 = energia potenziale del punto 2
U1 = energia potenziale del punto 1
Nel caso di un campo
elettrico E generico
U 2  U1  q0
2
 E  dr
1
La Forza elettrica è conservativa  W12 non dipende dal cammino di integrazione percorso della carica
q0 nel campo generato dalla carica q.
Se il punto P1 coincide con P2 (percorso chiuso)
W12  U2  U1  0
Circuitazione di F = 0  Forza elettrica conservativa
ma poichè

W12  l F dr 0
l F dr   q 0 l E dr  0
Allora anche la circuitazione di E = 0  Campo elettrico conservativo
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
2
Potenziale elettrostatico
U

q0
Definito come Energia potenziale per unità di carica
Unità di misura nel sistema SI: volt=joule/coulomb (V = J C-1)
Differenza di potenziale elettrico
Nel caso della carica puntiforme
W12 U2  U1
2  1 

q0
q0
 1
1 
2  1 
  
4  0  r2 r1 
q
Di solito si sceglie la condizione al contorno di potenziale nullo all’infinito,
per cui

1
q
4  0 r
Nel caso di una distribuzione continua di carica, il potenziale vale:
dove
(dq   dV; dq   dS; dq   dl)
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
1  0
r1  

1
4  0

dq
r
3
Le unità di misura - l’elettron-Volt
Dalla definizione di potenziale si evince che esso è il lavoro per unità di carica
necessario per portare l’unità di carica dall’infinito alla posizione r
Dal punto di vista dimensionale è un’energia per unità di carica
U
 
Pertanto il potenziale si misura in volt = joule / coulomb



q
1 joule rappresenta il lavoro (cioè l’energia) necessario per spostare l’unità di carica (1
coulomb) attraverso la d.d.p. di 1 volt.
Una definizione alternativa, usata in fisica atomica, consiste nel definire l’unità di
misura del potenziale nel modo seguente: il lavoro (cioè l’energia) necessario per
spostare la carica elementare (1|e| =1.6 10-19 coulomb) attraverso la d.d.p. di 1 volt. Tale
lavoro è pari a 1.6 10-19 joule, e tale valore viene chiamato elettron-volt (eV).
Pertanto 1 eV = 1.6 10-19 J (l’eV è un’unità di misura dell’energia).
Inoltre, si ricorda che, per definizione di potenziale,
2  1   E  dr
Quindi    EL dove Llunghezza, e pertanto l’unità di misura del campo elettrico
è, oltre che newton/coulomb, anche volt/m (ovviamente numericamente le due
grandezze sono equivalenti).

Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
Superfici equipotenziali e linee di forza
Le superfici equipotenziali sono definite come il
luogo dei punti per cui  = costante
Le linee di forza sono “linee” tangenti in ogni punto
alla direzione del campo elettrico
Campo elettrico uniforme
Lezione n. 4
Esempi
Carica puntiforme
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
Dipolo elettrico
5
Come calcolare il potenziale, dato E?
Si è visto che
U 2  U1  q0
2
 E  dr
2  1    E  dr
cioè
1
Tale risultato è indipendente dal
percorso
Nel caso in cui, poi, si scelga 1=0 la
formula si semplifica in:
2    E  dr
Nel caso della carica puntiforme, si ha:

    E  dr 
r
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
q
40 r
6
Esempio: potenziale di distribuzioni
sferiche
Guscio sferico o sfera conduttrice
Sfera uniformemente carica
All’interno il campo elettrico è Eint  0
All’esterno, il campo elettrico è Eest 
Q
40 r 2
come nel caso di una carica puntiforme.
Il potenziale all’interno va calcolato come
somma di due contributi, uno relativo a r<R,
dove il campo elettrico è Eint, e l’altro per r>R,
dove il campo elettrico vale Eest:
R

R

r
R
r
R
Vint   E int  dr   E est  dr   Eint dr  
Q
Eest dr  0 
40


R
dr
Q

2
40 R
r
Il potenziale all’esterno invece va calcolato solo
per r>R, dove il campo elettrico vale Eest:


r
r
Vest   E est  dr   Eest dr 
Lezione n. 4
Q
40


r
Eint 
All’interno il campo elettrico è

dr
Q 1
Q


2
40 r r 40 r
r
All’esterno, il campo elettrico è
Eest 
Qr
40 R 3
Q
40 r 2
come nel caso di una carica puntiforme.
Il potenziale all’interno va calcolato come
somma di due contributi, uno relativo a r<R,
dove il campo elettrico è Eint, e l’altro per r>R,
dove il campo elettrico vale Eest:
R

R
r
R
r

Vint   E int  dr   E est  dr   Eint dr   Eest dr 

 dr 
Q  R rdr
Q 3R  r


40 r R 3 R r 2 
80 R 3
2
2

R
Il potenziale all’esterno è uguale al caso del
guscio sferico poichè le distribuzioni a
simmetria sferica, per la legge di Gauss,
possiedono lo stesso campo di una carica
puntiforme posta al centro della distribuzione.
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Il potenziale in un campo elettrico
uniforme
Data la particolare geometria del
sistema, si ha subito:
E  dr  Edr cos  Edr
E pertanto la d.d.p. risulta essere:
2
2
2
1
1
1
2  1    E  dr    Edr   E  r   Ed
Dove “d” è la distanza di integrazione.
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Il potenziale di dipolo
Un dipolo elettrico è un sistema composto da due
cariche elettriche uguali ma di segno opposto poste
alla distanza d.
Il potenziale è una grandezza additiva, per cui nel
punto P, posto alla distanza r>>d, esso sarà dato da:
 q    q r( )  r(  )
1  q

40  r(  )
r(  )  40 r(  ) r(  )
Data la relazione tra d ed r, si possono utilizzare le
approssimazioni:
L’angolo  è compreso tra
V  V(  )  V(  ) 
r( )  r( )  cos
r( ) r(  )  r 2
l’asse del dipolo elettrico e
la direzione di P.
E quindi ottenere il valore finale per il potenziale:
La grandezza
p=qd
è definita
momento di dipolo elettrico
qd cos 
1 p cos 
V 

2
40 r 2
40 r
Si noti come per una carica puntiforme Vr-1 ed Er-2 mentre per un dipolo
elettrico Vr-2 ed Er-3 (nella direzione dell’asse).
Questo avviene perché si fa sentire l’effetto della seconda carica di segno opposto
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Il potenziale di un conduttore carico
isolato
In un conduttore carico isolato E=0 in tutti i punti all’interno di esso, e tutta la sua
carica giace sulla superficie del conduttore.
Dall’equazione che definisce il potenziale:
2  1    E  dr
Si deduce che essendo E=0 allora il potenziale è uguale per
tutte le coppie di punti possibili all’interno del conduttore.
Ad esempio, per un conduttore a forma di guscio sferico
campo elettrico e potenziale assumono l’andamento a fianco
Questo significa che le cariche
elettriche in un conduttore, in
presenza di campo elettrico, si
ridistribuiscono sulla superficie
in modo da assumere una
configurazione equipotenziale.
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
L’effetto parafulmine
Consideriamo due sfere con cariche Q1 e Q2 e raggi R1 << R2 collegate tra loro (cioè si
trovano allo stesso potenziale) e poste a grande distanza l’una dall’altra (quindi i loro
campi elettrici non si influenzano l’uno con l’altro all’interno delle sfere).
L’uguaglianza del potenziale implica che:
Da cui si trova: Q1  Q2
V1 
Q1
40 R1
R1
R2
Per quanto riguarda i campi elettrici, il loro rapporto vale:
E tenendo conto della relazione precedente, si ha:
 V2 
Q2
40 R2
Q1
E1 40 R12

Q2
E2
40 R22
E1 R2

E2 R1
Dato che R1 << R2 , allora E1 >> E2 .
Nel caso del parafulmine, R2  6000 Km è il raggio di curvatura della superficie terrestre mentre R1
 1 cm può essere assunto come il raggio di curvatura della superficie di un’asta metallica che funge
da parafulmine, per cui E1/E2  6 108
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
11
Potenziale dovuto ad una carica
lineare
Una sbarretta lunga L e sottile (spessore<<L) è carica positivamente
con densità lineare di carica data da dq  dx
Il potenziale dovuto alla bacchetta in un punto P, alla distanza d da
un suo estremo, può essere valutato integrando sulla bacchetta i
contributi dovuti agli elementi infinitesimi dq:
dV 
dq
1
dx

40 r
40 x 2  d 2
1


1
2
L
V   dV  
Tale integrale vale:
0


4 0
Si ricorda che l’integrale seguente è
risolubile come:

x2
x1
x
dx
2
d
2

 ln x  x  d
2
2
x2
x1
1
0

4 0 x 2  d 2
L

dx
x


dx
2
d
2

1

1

2

2


L

2
2

ln x  x  d

0
4 0


ln L  L2  d 2  ln d 
4 0


L  L2  d 2

ln
4 0
d
Lezione n. 4
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
12
Potenziale dovuto ad un disco carico
Si consideri un disco di raggio R, carico con densità di carica
superficiale =dq/dA. Il potenziale nel punto P, situato
sull’asse del disco, è valutabile considerando dapprima il
contributo di un anello infinitesimo del disco, di raggio R’ e
larghezza radiale dR’, di area 2R’ dR’ e carico dq.
dq   2R'dR'
Essendo tutti i punti dell’anello alla distanza r dal punto P, il
potenziale da essi generato vale:
dV 
dq
1  2R'dR'

40 r
40 z 2  R' 2 12
1


Il potenziale dovuto a tutto il disco è quindi dato dall’integrale:
dq

V   dV 

40 r
2 0
1
Lezione n. 4
 z
R
0
2
 R'

1
2  2
R' dR' 

2 0
z
2
 R2  z
Corso di Fisica B, C.S.Chimica, A.A.
2001-02

13
Energia potenziale elettrica
Ogni sistema di cariche possiede un’energia intrinseca immagazzinata nel sistema stesso: l’energia
potenziale elettrica
L’energia potenziale elettrica è definita come il lavoro richiesto per costruire il sistema di cariche,
spostando ciascuna carica da una distanza infinita alla propria posizione.
Ad esempio, si consideri un sistema di due cariche q1 e q2 poste alle distanze r1 e r2 da un arbitrario
sistema di riferimento. L’energia potenziale elettrica di questo sistema è equivalente al lavoro
necessario per portare la carica q2 dalla distanza infinita alla posizione r2 contro il campo elettrico
creato da q1:
1 q1
qq
V12 
U 12  L  V12 q 2  1 2
40 r12
40 r12
qq
Nel caso vi siano tre cariche q1, q2 e q3, prima considero la coppia q1 e q2, per cui U 12  1 2
40 r12
Poi considero q3: per portarla alla posizione r3 debbo prima compiere lavoro contro il campo generato
da q1
U 13 
q1 q3
40 r13
e poi contro quello generato da q2
Per cui il lavoro complessivo vale L  U  U 12  U 13  U 23 
Nel caso generale di un sistema di N cariche
Lezione n. 4
U 23 
q 2 q3
40 r23
qq
qq
q1q 2
 1 3  2 3
40 r12 40 r13 40 r23
1 N qi q j
U 
2 i  j 1 40 rij
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
14