1,5 MB

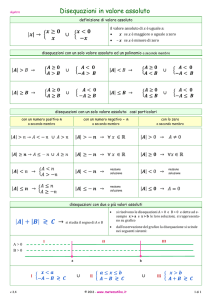
Le disequazioni
Disuguaglianze numeriche
I simboli > e < esprimono delle disuguaglianze.
ESEMPI
4 < 12
5 > −3
• ab
Il numero a è maggiore del numero b
• a≤b
Il numero a è minore di b o uguale a b
• a≥b
Il numero a è maggiore di b o uguale a b
• aa
• a≤b
equivale a
b≥a
1
Le disequazioni
• a3
9−4<3−4
infatti
9 > −1
1 > 1
a
b
a e b concordi
ESEMPI
infatti
−3 < −2
−
1
1
>−
3
2
−3 < 5
−
1
1
<
3
5
2
Le disequazioni
• a −3
• a −3  6
ac > bc
con
infatti
12 > −18
c negativo
ESEMPI
8 > −3
Caso particolare:
-12 < 3
8  (−2) < −3  (−2) infatti −16 < 6
Se
c=−1
a −b
12 > −3
3
Le disequazioni
Definizioni e caratteristiche
Una disequazione è una relazione della forma
A(x) > B(x)
oppure
A(x) < B(x)
nella quale si chiede per quali valori della variabile x l’espressione A(x) assume valori maggiori oppure
minori dell’espressione B(x).
• Risolvere una disequazione significa determinare i valori di x per i quali l’espressione A(x) assume
valori maggiori (o minori) dell’espressione B(x).
• Una disequazione è in forma normale se è scritta nel seguente modo: E(x) > 0 oppure E(x) < 0.
• Dominio: insieme dei valori che può assumere la variabile x
• Insieme delle soluzioni: tutti i valori della variabile x che rendono vera la disequazione
• Disequazioni equivalenti: disequazioni con lo stesso insieme di soluzioni
• Grado di una disequazione intera in forma normale: grado di E(x)
4
Le disequazioni
Definizioni e caratteristiche
• Disequazione intera: disequazione in cui A(x) e B(x) sono polinomi.
ESEMPIO
x + 3 > 2x – 4
1
x
x+
>1
3
4
• Disequazione frazionaria: disequazione in cui le frazioni algebriche contengono l ’ incognita al
denominatore.
ESEMPI
1 > 3x + 1
x
x > x+1
4
3
È frazionaria
È intera
5
Le disequazioni
Definizioni e caratteristiche
• L ’ insieme delle soluzioni è di solito un insieme di numeri reali che può essere rappresentato
graficamente sulla retta.
• Tutti gli insiemi rappresentati sulla retta reale da semirette o da segmenti vengono detti intervalli.
ESEMPIO
La disequazione x − 2 ≥ 0 ha come insieme delle soluzioni tutti i numeri reali che sono maggiori o
uguali a 2:
2
La disequazione x − 3 < 0 ha come insieme delle soluzioni tutti i numeri reali che sono minori di 3:
3
6
Le disequazioni
Rappresentazione delle soluzioni
Intervallo
Scrittura algebrica
ILLIMITATO APERTO
x>a
ILLIMITATO CHIUSO
x≥a
ILLIMITATO APERTO
x<a
ILLIMITATO CHIUSO
x≤a
LIMITATO APERTO
a<x<b
LIMITATO CHIUSO
a≤x≤b
LIMITATO APERTO A SX E CHIUSO A DX
a<x≤b
LIMITATO CHIUSO A SX E APERTO A DX
a≤x<b
Rappresentazione
sulla retta reale
a
a
a
a
a
b
a
b
a
b
a
b
7
Le disequazioni
Principi di equivalenza
Primo principio. Se ai due membri di una disequazione si aggiunge una stessa espressione C(x)
avente lo stesso dominio, si ottiene una disequazione equivalente a quella data e dello stesso verso:
A(x) > B(x)
è equivalente a
A(x) + C(x) > B(x) + C(x)
Conseguenza. Si possono spostare termini da un membro all’altro cambiando loro il segno:
ESEMPIO
5x – 4 > 2x + 7
è equivalente a
5x – 2x > 7 + 4
8
Le disequazioni
Principi di equivalenza
Secondo principio. Se si moltiplicano i due membri di una disequazione per uno stesso numero positivo
k, si ottiene una disequazione equivalente a quella data e dello stesso verso:
A(x) > B(x) e
k>0
è equivalente a
k  A(x) > k  B(x)
Se si moltiplicano i due membri di una disequazione per uno stesso numero negativo k, la disequazione
che si ottiene è equivalente a quella data solo se si cambia anche il verso:
A(x) > B(x) e
k<0
è equivalente a
k  A(x) < k  B(x)
Conseguenza. Si possono dividere i due membri di una disequazione per uno stesso numero
rispettando il secondo principio.
ESEMPI
3x + 3 > 6
−10x + 5 > −15
dividendo per 3 è equivalente a
dividendo per −5 è equivalente a
x+1>2
2x − 1 < 3
9
Le disequazioni
Principi di equivalenza
Conseguenza. Si possono cambiare i segni ai termini dei due membri di una disequazione ma bisogna
cambiare anche il verso perché questa operazione equivale a moltiplicare per −1.
ESEMPIO
−6x + 3 < 4 −5x
diventa
6x − 3 > 5x − 4
Conseguenza. Se nella disequazione ci sono denominatori numerici, si può trasformare la disequazione
in modo da avere coefficienti interi moltiplicando per il m.c.m. fra i denominatori.
ESEMPIO
x−1
2
+
3x − 4
3
>
1
6
x
diventa
6
3(x − 1) + 2(3x − 4)
3(x – 1) + 2(3x – 4) > x
6
>
x
6
6
continua
10
Le disequazioni
Principi di equivalenza
ATTENZIONE! L ’ ultima conseguenza non può essere applicata alle disequazioni frazionarie per
eliminare i denominatori.
ESEMPIO
x+1
x
−
>0
x−1
x
Non è equivalente a
(x + 1)(x – 1) – x2 > 0
11
Le disequazioni
Disequazioni lineari intere
Disequazione lineare intera: disequazione intera di primo grado.
Procedura risolutiva
• Si eseguono le operazioni indicate e si eliminano gli eventuali denominatori.
• Si trasportano tutti i termini contenenti la x al primo membro e gli altri al secondo e si riducono poi gli
eventuali termini simili.
• Si ottiene una disequazione ridotta in forma normale del tipo ax > b oppure ax < b.
• Se a ≠ 0 si dividono entrambi i membri per a ricordando di cambiare il verso della disuguaglianza se
a < 0.
• Se a = 0 la disequazione si riduce a una disguaglianza che può essere vera o falsa, determinando
così un insieme di soluzioni uguale a R o all’insieme vuoto.
NOTA
Se a < 0 conviene prima cambiare segno e verso alla disequazione.
12
Le disequazioni
Disequazioni lineari
Schema riassuntivo – Risoluzione ax > b
ax > b
a>0
x>
b
a
b/a
a<0
b
x<
a
b/a
a=0
b≥0
S=
b<0
S=R
0>b
13
Le disequazioni
Disequazioni lineari
ESEMPIO
2(x − 1) + 3x > 7(2x – 1)
2x − 2 + 3x > 14x – 7
• Svolgiamo i calcoli:
5x − 2 > 14x – 7
• Separiamo
i
termini
l’incognita dai termini noti:
con
5x − 14x > –7 + 2
−9x > –5
• Cambiamo segno e verso:
9x < 5
• Dividiamo per il coefficiente di x:
x<
• Rappresentiamo la soluzione sulla
retta dei numeri:
5
9
5/9
14
Le disequazioni
Disequazioni frazionarie
Procedura risolutiva
• Dopo aver posto le condizioni di esistenza si portano tutti i termini della disequazione al primo membro
• Si riducono tutte le frazioni allo stesso denominatore e si svolgono i calcoli in modo da arrivare alla
forma
A(x)
B(x)
>0
oppure
A(x)
B(x)
<0
• Si studiano separatamente i segni di A(x) e di B(x)
• Si riporta la variazione dei segni di ciascun polinomio in una tabella
• Si costruisce il segno della frazione
• Si scelgono gli intervalli delle soluzioni in base al verso
15
Le disequazioni
Disequazioni frazionarie
ESEMPIO
x+2
2x
>1−
x+3
x+3
• Trasportiamo tutti i termini al primo membro:
• Riduciamo tutto allo stesso denominatore:
• Svolgiamo i calcoli al numeratore
x ≠ −3
x+2
2x
>0
−1+
x+3
x+3
2x – (x + 3) + x + 2
>0
x+3
2x – 1
>0
x+3
continua
16
Le disequazioni
Disequazioni frazionarie
ESEMPIO
• Segno del numeratore:
2x – 1 > 0
se
1
x>
2
−
+
R
+
R
1
2
• Segno del denominatore:
x+3>0
se
−
x>−3
−3
1
−3
• Costruiamo la tabella dei segni:
• Calcoliamo il segno della frazione:
• Scriviamo le soluzioni:
2
−
−
+
−
+
+
+
−
+
x<−3
∨
x>
1
2
17
Le disequazioni
Disequazioni non lineari
Disequazione non lineare: disequazione del tipo A(x) > 0 o A(x) < 0 con grado di A(x) > 1
Procedura risolutiva (nel caso A(x) scomponibile in fattori di 1° grado):
• Si scompone il polinomio A(x) in fattori di primo grado
• Si studia il segno di ogni fattore
• Si costruisce la tabella dei segni
• Si determina il segno del polinomio in ogni intervallo individuato
• Si individua l’insieme delle soluzioni
18
Le disequazioni
Disequazioni non lineari
ESEMPIO
x2 – 4x + 3 < 0
(x − 1) (x – 3) < 0
• Scomponiamo il trinomio con la regola del trinomio caratteristico:
• Studiamo il segno di ogni fattore:
3
1
(x – 1) > 0
se
x>1
−
+
+
(x – 3) > 0
se
x>3
−
−
+
• Calcoliamo il segno del polinomio:
+
−
+
• Scriviamo le soluzioni:
1<x<3
19
Le disequazioni
Sistemi
Sistema di disequazioni in una incognita: insieme di due o più disequazioni nella stessa incognita che
devono essere verificate contemporaneamente.
Insieme delle soluzioni: Intersezione degli insiemi soluzioni delle disequazioni che viene trovata con la
tabella delle soluzioni.
ESEMPIO
1
x−1>0
2
3x – 1 > 0
x>2
Risolvendo le due disequazioni si
ottiene il sistema:
x>
1
3
S1
S2
1
Rappresentiamo gli insiemi S1 e S2
nella tabella delle soluzioni e
determiniamo la loro intersezione:
3
2
S1
S2
S
20