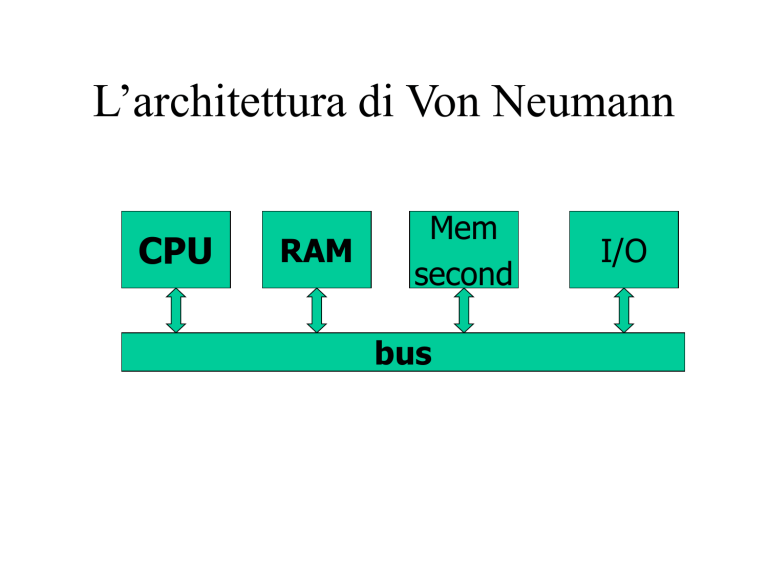
L’architettura di Von Neumann
CPU
RAM
Mem
second
bus
I/O
RAM = Random Access Memory
memoria ad accesso casuale
Nella RAM, come ovunque in un computer, le
informazioni sono rappresentate con sequenze di 0 e
di 1. Numeri binari.
La RAM quindi è fatta per contenere tali numeri.
•un bit può contenere o 0 o 1
•un byte è una sequenza di 8 bits
•una parola consiste di 4 bytes
bit
quindi la RAM è
una sequenza di bytes
da cui si leggono ed in
cui si scrivono singoli
byte o blocchi di 4
bytes consecutivi: le
parole.
byte
parola
Indirizzamento di byte e parole
byte
0
1
2
3
4
5
6
7
8
9
10
11
parola
in binario
0
00000000
00000001
00000010
00000011
1
00000100
00000101
00000110
00000111
2
00001000
00001001
00001010
00001011
unità di misura della RAM
1 Kilo byte: 210 = 1024 bytes, 1000
1 Mega byte: 220 = 1.048.576 bytes, 1000000
1 Giga byte 230 = 1.073.741.824 bytes, 109
1 Tera byte 240 = 1.099.511.627.776 bytes, 1012
Caratteristiche della RAM
• RAM accedere ad ogni byte ha la stessa
durata (10-7 sec): non dipende da quale byte
è stato acceduto prima
• è volatile: se tolgo la spina l’informazione è
persa (c’è anche la ROM)
• ogni byte ha un indirizzo 0,1,2......
• il byte è la minima quantità accessibile
(attraverso il suo indirizzo)
La CPU: unità centrale di calcolo:
esegue programmi che sono nella RAM
bus
CPU
registri di
calcolo
R0
Rn
ALU
RC
P
CI1
CI2
CIk
IP
RAM
La CPU esegue continuamente il ciclo
ADE=Access/Decode/Execute
• Access: preleva dalla RAM la prossima
istruzione da eseguire (l’indirizzo è in P,
l’istruzione viene messa in IP)
• Decode: decifra il codice dell’istruzione I che
si trova memorizzata in IP
• Execute: la esegue attivando il circuito CI
Memoria Secondaria:
• è permanente
• dischi fissi, floppy, nastri magnetici, CD
• accesso sequenziale o misto (il tempo varia
a seconda dell’accesso precedente)
• è adatta per leggere/scrivere grandi
quantità di dati (in posizioni contigue)
I/O = Input/Output
Dispositivi di comunicazione utente
computer. In un personal computer:
• Input = tastiera
• output = video / stampanti
• velocità diverse e molto minori delle
altre parti del computer (decimi di sec)
Rappresentazione dei dati
nella RAM
I dati fondamentali sono:
INTERI, REALI e CARATTERI
Il computer ha memoria finita e quindi
l’insieme dei numeri interi rappresentabili,
quello dei numeri reali rappresentabili e
quello dei caratteri rappresentabili sono
necessariamente finiti.
Gli interi nel computer
Generalmente gli interi occupano una
parola di 32 bit: in tutto 232 numeri distinti.
Con n bit bn-1…b1b0 si rappresentano
interi positivi da 0 a 2n-1:
x bn1 2
n 1
b1 2 b0 2 i 0 bi 2
1
n 1
0
i
xmin i 0 0 2 0
n 1
e i negativi ?
i
xmax i 01 2 2 1
n 1
i
n
Riserviamo il primo bit per il segno:
0 = positivo
1 = negativo.
I numeri positivi rappresentabili sono
quelli compresi tra 0 e 2n-1-1
Vi sono due modi per rappresentare i
numeri negativi detti rispettivamente
rappresentazione con complemento a 1
e con complemento a 2.
Complemento a uno
Si complementa a 2n-1 il valore assoluto
del numero.
Esempio con n = 6 bit: la rappresentazione
di –10 è:
6310=
--53
in binario
111111001010=
------110101
Problemi:
• 2 rappresentazioni per lo 0: +0 e –0
63111111in binario
0=
000000=
--------63
111111
Concludendo: con n = 6 si rappresentano i numeri:
Rappr.
0
1 ...
31
32 ...
63
Numero
0
1 ... 31
positivi
-31 ...
negativi
-0
• complicata realizzazione delle operazioni aritmetiche
Complemento a due
Si complementa il valore assoluto del
numero a 2n invece che a 2n-1.
Esempio con n = 6 bit: la rappresentazione
di –10 è:
6410=
--54
in binario
1000000001010=
------0110110
Complementando 0 si ottiene ancora 0
64in binario
0=
--64 ha gli ultimi 6 bit uguali a 0
1000000000000=
------1000000
Complementando 54 (che rappresenta –10)
si ottiene
641000000in binario
54=
--10 ha il bit 5 uguale a 0(positivo)
110110=
------0001010
Complementando 32 (che rappresenta –32)
si ottiene
64in binario
32=
--32 ha il bit 5 uguale a 1(negativo)
1000000100000=
------0100000
Concludendo: con n = 6 si rappresentano i numeri:
Rappr.
0
1 ...
31
32 ...
63
Numero
0
1 ... 31
positivi
-32 ...
negativi
-1
In generale: con n bits
positivi
negativi
0 .... 2n-1-1
-2n-1 .... -1
La somma è semplice (n = 6)
Somma di numeri positivi: 10+12
10+
12=
--22
riporto 001000
001010+
in binario
001100=
I due ultimi riporti ------sono uguali
0010110
Somma di numeri negativi: (-10)+(-12)
-10 64-10 = 54
54+
52=
--106
-12 64-12 = 52
riporto 110100
110110+
in binario
110100=
------I due ultimi riporti
1101010
sono uguali
106-64=42
64-42 = 22
bit di overflow
complemento
-22 64-22= 42
verifica
Somma con un numero negativo (-10)+12
-10 64-10 = 54
riporto
54+
12=
--66
66-64 = 2
in binario
I due ultimi riporti
sono uguali
111100
110110+
001100=
------1000010
Risultato troppo grande 27+12 = -25
errore di overflow
27+
12=
--39
riporto
in binario
I due ultimi riporti
sono diversi
64-39 = 25
011000
011011+
001100=
------0100111
-25 64-25= 39









