Fibre ottiche

FIBRE OTTICHE
Fibre ottiche: caratteristiche
• piccole, diametro 125 mm, e < 1 mm con rivestimento plastico
• leggere e flessibili, curvabili anche con diametri di qualche mm
• nessuna corrosione e stabili chimicamente
• basse attenuazioni, 0.4 dB/km a 1.3 mm, 0.2 dB/km a 1.5 mm
• grandi bande, graded index qualche GHz km, monomodali decine o
centinaia di GHz km
• libere da induzione elettromagnetica e danni da fulmini
• limitatissime diafonie
• resistenti ad alte temperature
• il contenuto informativo non è facilmente intercettabile
• la silice, di cui sono fatte, è abbondante, non così il rame
Richiami di ottica
Le onde luminose sono onde elettromagnetiche, come le onde radio, i
raggi X e i raggi gamma: l’unica differenza è nella frequenza. Ad
esempio, per lo spettro visibile
ultravioletto
infrarosso
0.66
0.44
energia (eV)
10 5
Radiazione non ionizzante
microonde
visibile
infrarosso
12 eV
10 0
Radiazione ionizzante
Raggi g
UV
Raggi X
10 -5
l (mm)
f l = c = 3 108 m/s
v = c/n, n indice di
rifrazione
E = h f energia
associata al fotone
h=6.6 10-34 W s/Hz
10 -10
10 5
10 10
10 15
Frequenza (Hz)
10 20
Rifrazione e riflessione
Se un raggio di luce incide sulla superficie di separazione di due mezzi
trasparenti si divide in un raggio riflesso e un raggio rifratto, secondo la
legge di Snell.
sin α  n2

sin  β  n1
b
Indice di
rifrazione n2 < n1
Indice di
rifrazione n1
a
a
Riflessione totale
Se a è tale che sin(b) = 1, ovvero b = p /2, e quindi sin(a) = n2/n1, non si
ha più raggio rifratto.
Superando tale angolo a si ha riflessione totale, a  arcsin(n2/n1).
angolo limite 
Indice di
rifrazione n2 < n1
Indice di
rifrazione n1
b
a
a
sin α  
n2
n1
Propagazione in fibra ottica
Dati due cilindri concentrici, se l’indice di rifrazione di quello interno è
maggiore di quello esterno, i raggi che incidono alla superficie di
separazione dei cilindri con angolo maggiore di quello limite subiscono
riflessione totale e si possono, così, propagare.
Nelle fibre, gli indici di rifrazione si possono variare drogando la silice
SiO2 (il cui indice di rifrazione è circa 1.45, variabile leggermente con la
lunghezza d’onda), con ossidi, quali, GeO2 , P2O5 , B2O3 .
n
angolo limite  sin α   2
n1
n2 < n1
a
a
n1
n2 < n1
Il cilindro interno è il core, quello esterno il cladding
Apertura numerica
Affinché i raggi che si propagano in fibra siano guidati, cioè gli angoli
di incidenza siano superiori a quello limite, i raggi incidenti dalla
sorgente debbono essere contenuti in un cono di accettazione, il seno
trigonometrico del cui angolo bM è detto apertura numerica (NA).
sin(bM )/sin(a’)=n1/na
n 2 < n1
Aria na
bM
Angolo limite sin(a) = n2/n1
a’
n2 < n1
n1
a
a
Apertura numerica
sin β M  sin β M  n1
Essendo


 n1 e
sinα' 
cosα 
na
n2
sinα  
 cosα  
n1
 n2 
1   
 n1 
2
2
 n2 
NA  sin β M   n1  cosα   n1  1    
 n1 
n12  n22
sin( bM )/sin(a’)=n1/na
n2 < n 1
Aria na
bM
Angolo limite sin(a) = n2/n1
a’
n1
a
a
n2 < n 1
Il cono di accettazione è tanto maggiore quanto maggiore è NA, e ciò è
positivo per l’accoppiamento con le sorgenti ottiche, ma questo ha effetti
negativi sulla banda della fibra.
Struttura fisica delle fibre per telecomunicazioni
250 mm
Rivestimento primario
125 mm
Mantello (cladding)
Nucleo (core)
Multimodo 50 mm
62.5 mm
Monomodo <10 mm
Fibre ottiche: attenuazione
Perdite di natura tecnologica
- perdite intrinseche: diffusione (scattering di Rayleigh), assorbimento
nell’ultravioletto, assorbimento nell’ infrarosso;
- perdite estrinseche: irradiazione (da curvature), assorbimento,
diffusione di idrogeno.
Perdite per interconnessione
- perdite intrinseche: differenti indici di rifrazione, differenza di N.A,
differenza diametri core
- perdite estrinseche: errori di disassamento, errori di separazione,
disallineamento.
Attenuazione di natura tecnologica
- Diffusione (Scattering di Rayleigh)
il raggio luminoso diffonde in tutte le direzioni, per disomogeneità della
fibra, piccole rispetto alla lunghezza d’onda (particelle con diversa
densità, bolle di aria, etc.). Avendo i raggi diffusi angoli di incidenza tra
core e cladding aleatori, la maggior parte non è guidata, con
conseguente attenuazione. Tali cause non sono eliminabili.
La perdita è del tipo p = W/l4 dB/km, ove W varia secondo la
costituzione chimica del core (tipo di droganti e loro concentrazione).
Valori orientativi sono dell’ordine di 0.3 dB/km @1310 nm, 0.15 dB/km
@1550 nm. Come è, allora, evidente, lo scattering di Rayleigh è il
meccanismo più importante di attenuazione delle fibre ottiche.
Attenuazione di natura tecnologica
- Assorbimento
è causato da impurità presenti nei materiali (ioni metallici di Fe, V, Ni,
Cu, Cr, etc) e principalmente di ioni ossidrili (OH), i quali presentano
picchi di assorbimento a 950, 1240 e 1390 nm, col che si definiscono le
finestre ottiche:
- la prima attorno a 850 nm (ad esempio, 800 - 900 nm),
- la seconda attorno a 1310 nm (ad esempio, 1290 - 1330 nm),
- la terza attorno a 1550 nm (ad esempio, 1530 - 1565 nm).
Le concentrazioni massime per limitare l’attenuazione sono sotto al ppb,
per i metalli, dell’ordine del ppb per l’ossidrile.
Attenuazione di natura tecnologica
- Perdite per diffusione di idrogeno
quando l'idrogeno diffonde nelle fibre, essendo presente nei materiali che
compongono il cavo, o nell’ambiente circostante, esso è intrappolato dal
cristallo di SiO2 , ad esempio un gruppo Si - OH, e le sue vibrazioni
causano perdite per assorbimento, per lunghezze d’onda maggiori di 1
mm.
Particolari materiali, come il fosforo, aggiunti alla silice per cambiare
l’indice di rifrazione, sono particolarmente critici e dovrebbero essere
evitati o ridotti al minimo possibile; si dovrebbe usare il fluoro come
drogante; i materiali da impiegare per la realizzazione di fibre e cavi
dovrebbero essere scelti con molta attenzione, al fine di limitare questo
effetto, tali, cioè, da non generare idrogeno.
Attenuazione di natura tecnologica
- Perdite per imperfezioni di guida
ove non sia rispettata la geometria ideale, longitudinale o trasversale (ad
esempio, a causa di variazione del raggio del core, deformazioni del core,
imperfezioni nell’interfaccia core/cladding, irregolarità longitudinali
nell’interfaccia core/cladding, etc.), si ha, nelle fibre monomodali, una
ulteriore attenuazione, indipendente dalla lunghezza d’onda, con valori
orientativi fino a 0.2 dB/km;
Se la precisione del raggio del core è minore dell’uno per cento, tali
attenuazioni residue sono dell’ordine del centesimo di dB/km.
Attenuazione di natura tecnologica
- Perdite per curvatura
in una fibra diritta, l’asse del fascio ottico e quello della guida
coincidono, mentre nella fibra curva il fascio ottico si sposta verso
l’esterno, e non coincide più con l'asse della fibra. Il campo è irradiato
fuori dal core, con conseguente attenuazione.
Le perdite aumentano esponenzialmente con la diminuzione del raggio
di curvatura R, con la diminuzione del quadrato dell’apertura numerica
NA e con l’aumento del raggio del core r ( e-(R·NA^2/r^2).
Nelle tipiche fibre monomodali, se i raggi di curvatura sono maggiori di
un cm, le perdite per curvatura sono minori del centesimo di dB/km,
quindi, sostanzialmente, irrilevanti.
Attenuazione di natura tecnologica
- Perdite per microcurvatura
la fibra nel cavo può essere soggetta a sollecitazioni che causano piccole
curvature, continue ed aleatorie, col che l’asse della fibra non è più
rettilineo e cambiano gli angoli di incidenza del fascio luminoso tra core
e cladding; si ha quindi irradiazione nel cladding ed attenuazione.
L’attenuazione per microcurvatura può derivare anche dai processi di
fabbricazione delle fibre e, se questi processi sono errati, le conseguenti
attenuazioni possono variare da qualche decimo sino ad alcuni dB/km.
Le fibre devono, quindi, evitare il più possibile stress esterni, durante la
fabbricazione e la posa. Essendo necessario proteggere meccanicamente
le fibre, tale protezione deve comunque limitare la trasmissione di stress,
come in seguito esaminato con maggiore dettaglio.
Le perdite per microcurvatura aumentano all’aumentare della lunghezza
d’onda e diminuiscono all’aumentare dell’apertura numerica.
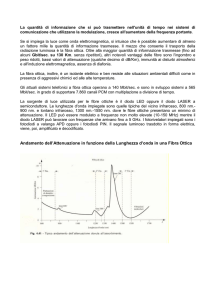
Attenuazione spettrale
Attenuazione dB/km
Assorbimento SiOH
0.95 mm 1.24 mm 1.39 mm
1
0.5
Scattering di Rayleigh
0.1
0.05
0.01
Assorbimento infrarosso
Assorbimento ultravioletto
0.8
1
1.2
1.4
Lunghezza d’onda mm
1.6
1.8
Tipi di fibre ottiche
- Fibre multimodali, il cui diametro del cladding, tipicamente 50 mm, è
molto maggiore della lunghezza d’onda della luce. Si propagano molti o
moltissimi “raggi” luminosi; si distinguono in
• step index, con variazione brusca dell’indice di rifrazione dal core
al cladding;
• graded index, con variazione graduale dell’indice di rifrazione dal
centro del core al cladding.
- Fibre monomodali, il cui diametro del cladding, tipicamente
dell’ordine dei 9 mm, è, da punto di vista elettromagnetico, dello stesso
ordine di grandezza della lunghezza d’onda della luce, tipicamente 1.3 1.5 mm. Si propaga un solo “raggio” luminoso.
Fibre Step Index - Dispersione Modale
I “raggi”, propagandosi a “zig-zag”, percorrono cammini diversi, in
relazione alla loro diversa inclinazione rispetto all’asse della fibra, ciò che
causa tempi di propagazione diversi, quindi differenti ritardi in ricezione.
L
n 2 < n1
n1
Angolo limite sin(a) = n2/n1
a a
n2
n1
n 2 < n1
• Raggio diretto, tx = L/v = L n1 /c
• Raggio più lento ty = L n1 /( sin (a)·c) = L n1 /(n2/n1· c) = L n12 /(n2 c)
Dt = Ln1· (n1 - n2 ) / c n2 tanto maggiore quanto maggiore è l’apertura
numerica, tipicamente NA dell’ordine di 0.2 (n1  1.5, (n1 - n2 ) < 0.01).
• Anche se (n1 - n2 ) = 0.003, banda  1/ Dt  100 MHz km @ 0.8 mm, quindi
prestazioni limitate.
Fibre Step Index: caratteristiche orientative
• Diametro 50/125 mm
• D = (n1 - n2 ) / n1  1 % (NA  0.21)
• Propagazione multimodale
• Attenuazione @ 0.85 mm  2.6 dB/km, @ 1.3 mm  0.4 dB/km
• Banda @ 0.85 mm  40 MHz km
Fibre Graded Index
n2
n1
L’indice di rifrazione nel core non è costante, ma decresce dal centro alla
periferia, massimo valore n1 , minimo n2 . Per lo più, tale andamento è
quasi parabolico, in funzione del raggio r, secondo la relazione generale
α

r 
nr   n1  1  Δ    

 ρ  
ρ raggio del core
Se a = 2, la fibra
è detta a indice
parabolico.
Fibre Graded Index: caratteristiche orientative
•Diametro 50/125 mm
D = (n1 - n2 ) / n1  1 % (NAmax  0.21)
• Propagazione multimodale
• Attenuazione @ 0.85 mm 2.6 dB/km, @ 1.3 mm 0.4 dB/km, @ 1.55 mm
0.25 dB/km
• Banda @ 0.85 mm e @ 1.3 mm qualche GHz km
Dispersione modale
Nelle fibre multimodali (come quelle step index e graded index appena
esaminate), la propagazione di segnali ottici numerici avviene
distribuendo la potenza ottica tra i vari modi con cui la luce può
propagarsi nella fibra.
Ognuno di questi modi ha una diversa distribuzione del campo
elettromagnetico nell’interno della fibra, in funzione della coordinata
radiale e di quella angolare nel core (ad esempio, numero di massimi nelle
due coordinate dette) ed è caratterizzato da una propria velocità di
propagazione, in funzione della lunghezza d’onda.
In sostanza, ogni impulso si distribuisce, in modo più o meno uniforme,
tra i vari modi, sicché nella fibra si propagano in effetti molti impulsi
ottici, ciascuno associato ad un modo diverso, con una diversa velocità di
propagazione.
Dispersione modale
Tale allargamento temporale è, in prima, grossolana, approssimazione,
proporzionale alla lunghezza della tratta in fibra e dipende dalle
caratteristiche trasmissive della fibra stessa.
In “buone” fibre multimodali graded index, le massime velocità
trasmissive, riferite all’unità di lunghezza, sono di qualche Gbit/s . km.
La dispersione modale preclude, perciò, la possibilità di impiegare tali
fibre nei moderni sistemi di telecomunicazione, che, attualmente, hanno
velocità trasmissive di parecchi Gbit/s, su tratte dell’ordine anche del
centinaio di chilometri.
Fibre ottiche monomodali
Per ottenere bande molto grandi non è, quindi, possibile pensare di
compensare i ritardi relativi dei vari modi (che originano la dispersione
modale), operazioni di fatto irrealizzabile, ma, piuttosto, si deve impedire
la propagazione di più “raggi”, o modi guidati, nella guida ottica.
Per ogni modo vi é, infatti, una lunghezza d’onda al di là della quale tale
modo non si può propagare (decade esponenzialmente con la distanza),
tranne un modo, detto modo fondamentale, che si propaga comunque.
Ad es., nel caso di fibra step index, se si esamina la propagazione con le
equazioni di Maxwell, quando la frequenza normalizzata V è tale che
ω
V   a  n12  n22  2.405
c

λ
(c)
2  π  a  n12  n22
2  π  a  NA


2.405
2.405
ciò che corrisponde al primo zero della funzione di Bessel di ordine 0, si ha
il cut-off del modo superiore (HE01), e la fibra è monomodale, ovvero
supporta il solo modo fondamentale HE11 (diametro del core, 2a=8÷10 mm).
Fibre ottiche monomodali
Per ottenere la propagazione monomodale, il diametro del core deve
essere piccolo, dell'ordine dei 10 mm, circa 5 volte minore del diametro
delle fibre multimodali, e la lunghezza d’onda impiegata, come già detto,
deve essere superiore ad un valore minimo, lunghezza d’onda di taglio, o
di cut-off.
Si ha, quindi, assenza di dispersione modale, ma rimane comunque la
dispersione cromatica, dovuta alla differente velocità con cui ciascun
modo, e quindi anche il modo fondamentale, si propaga al variare della
lunghezza d’onda.
Tale dispersione è, tuttavia, di gran lunga meno intensa di quella modale
ed é minimizzabile impiegando lunghezze d’onda ove tale dispersione è
sostanzialmente nulla (zero di dispersione cromatica) o sorgenti molto
monocromatiche, come i laser. Tali fibre hanno reso quindi possibile la
realizzazione di sistemi a lunga tratta e altissima velocità trasmissiva.
Lunghezza d’onda di taglio
Come già detto, la lunghezza d’onda di taglio, cut-off, di una fibra ottica
è la lunghezza d’onda oltre la quale si può ritenere che si propaghi il
solo modo fondamentale, talché la fibra si può considerare realmente
monomodale.
Da ciò la grande importanza operativa di questo parametro e la
necessità di una sua accurata conoscenza.
Il valore teorico della lunghezza d’onda di taglio è calcolabile a partire
dalle caratteristiche ottiche e geometriche della fibra, in particolare
dalla struttura del core e dall’andamento del coefficiente di rifrazione.
Nella pratica, tuttavia, la lunghezza d’onda di taglio è un parametro dai
contorni sfumati, proprio per le particolari condizioni di propagazione
nelle fibre ottiche, che risente delle effettive condizioni geometriche e
meccaniche della fibra stessa.
Il modo fondamentale
Dato che le componenti assiali Ez e Hz sono piccole, per D =(n1-n2)n1 << 1,
allora il modo fondamentale HE11 è, in prima approssimazione,
polarizzato linearmente (LPx)01, nelle fibre debolmente guidanti.
Assumendo Ey = 0, si ha, allora,
 J 0 κ  ρ
 e jβz

J 0 κ  a 
E x  E0 
 e jβz
 K 0 γ  ρ
K 0 γ  a 

ρa
ρa
ε0
H y  n2 
 Ex
μ0
E0 dipende dalla potenza del modo; i parametri sono legati dalle relazioni
κ n k  β
2
2
1
2
0
2
γ  β n k
2
2
2
2
2
0
ω 2π
k0  
c
λ
Il modo fondamentale
Il modo fondamentale è polarizzato linearmente lungo l’asse x.
La fibra supporta anche un modo fondamentale polarizzato
linearmente lungo l’asse y (LPy)01.
Pertanto, la fibra singolo modo supporta due modi di polarizzazione,
ortogonali, (LPx)01 e (LPy)01 , teoricamente degeneri: tale situazione
origina la dispersione di polarizzazione, in quanto, all’atto pratico, la
fibra ottica non può essere considerata un mezzo dielettrico omogeneo.
In particolare, come conseguenza, i due modi linearmente polarizzati
hanno velocità di propagazione diverse.
Dispersione cromatica
Nelle fibre monomodali, come si è visto, si evita la dispersione modale.
La sorgente ottica, però, emette potenza non a una sola lunghezza d’onda,
ma su un intervallo di lunghezze d’onda (decine di nm per i LED, Light
Emitting Diode, nm o frazioni di nm per i laser a semiconduttore).
La velocità di propagazione della luce in fibra, anche per un singolo modo,
varia con la lunghezza d’onda, sia perché così varia l’indice di rifrazione
del materiale della fibra (dispersione di materiale) sia perché, al variare
della lunghezza d’onda, muta la struttura del campo elettromagnetico nella
fibra, con conseguente variazione di velocità (dispersione di guida).
Le diverse componenti cromatiche dell’impulso ottico viaggiano, quindi,
con velocità diverse, causando allargamenti temporali; tale dispersione è
comunque modesta e consente di realizzare collegamenti a decine di Gbit/s
su decine o centinaia di chilometri. Al riguardo, le fibre monomodali
standard hanno lo zero di dispersione cromatica in seconda finestra (1.31
mm), le fibre a dispersione spostata in terza (1.55 mm).
Dispersione di materiale e di guida
l = lc
l = lc+20%
Modulo del
campo elettrico
E(r/r)
l = lc+40%
-3
Dispersione di materiale
la velocità di propagazione
varia, a seconda dei materiali
con cui è realizzata la fibra
ottica, con la lunghezza
d’onda, poiché varia l’indice
di rifrazione di tali materiali.
-2
-1
1
r / raggio del core r
2
3
Dispersione di guida
la velocità di propagazione varia con
la lunghezza d’onda, in quanto,
variando la lunghezza d’onda, varia la
struttura del campo elettromagnetico
in fibra e cambia, di conseguenza,
anche la velocità di propagazione.
Fibre monomodali – Dispersione cromatica
Andamento della dispersione di materiale e di quella di guida per fibre
ottiche singolo-modo SM, DS e Dispersion-Flattened.
Fibre monomodali – Dispersione cromatica
Le diverse lunghezze d’onda che compongono l’impulso trasmesso,
associate alla larghezza spettrale finita della sorgente ottica, si propagano
con diversa velocità nella fibra, componendosi, al termine di essa, con
ritardi diversi e corrispondenti allargamenti temporali
Fibra monomodale
Laser
Fotodiodo
 τ λ
1  2 τ λ
L  D λ 
2
2
Δτ 
 Δλ  

Δλ

.
.

L

D

Δλ



Δλ
 ..
2
λ
2 λ
2
λ
L  D  Δλ 
L
 S  Δλ 2  . .
2
D ps/kmnm
S ps/kmnm 2
ove S = dD/dl. La dispersione cromatica è un effetto deterministico che
può essere efficacemente compensato (ad es., fibre compensatrici).
Fibre monomodali – Dispersione cromatica
In generale, in assenza di distorsioni di ampiezza, la propagazione in un
canale lineare può essere esaminata a partire dall’andamento della fase
della funzione di trasferimento f(w) = b(w)·z , avendo esplicitato la
dipendenza della fase dalla distanza
 1
n
 ω  β ω  z    βn ω  ω0    z
 n0 n!

 n β ω
βn 
ω n ω
0
La velocità di fase è w0/b0, la velocità di gruppo è 1/b1.
La dispersione cromatica, ovvero la dispersione della velocità di
gruppo, è dovuta, nei sistemi in fibra ottica, alla variazione della
velocità di gruppo con la frequenza o, meglio, con la lunghezza d’onda.
Fibre monomodali – Dispersione cromatica
Come già indicato, per misurare la dispersione cromatica è impiegato il
parametro D, espresso in ps/km·nm; si ha, allora, riferendosi per le fasi
ad un km di fibra (come per il parametro D)
d 1
d dβ ω 
2 π c d dβ ω
2 π c d 2 β ω
2πc
D

 2
 2


β2
2
2
dλ v g dλ dω
λ dω dω
λ
dω
λ
infatti
c
λ
f
c
λ2
λ2
 dλ   2 df   df  
dω
f
c
2πc
Fibre monomodali – Dispersione cromatica
Analogamente, il parametro S esprime la variazione del parametro D in
un certo intervallo di lunghezze d’onda; tale parametro è, inoltre,
particolarmente significativo anche in corrispondenza della “dispersione
nulla”, ovvero ove D = 0; procedendo come in precedenza,
dD
d  2 π c d 2 β ω 
2 π c d  2 π c d 2 β ω 
S
  2
 2
 2

2
2
dλ
dλ  λ
dω 
λ dω  λ
dω 
2 π c d  2 π c  d 2 β ω  2 π c  d  d 2 β ω 
4πc
 2πc
 2

 2 

   3  β2   2  β3
2 
2
2

λ dω  λ  dω
λ
 λ  dω  dω 
 λ 
2
infatti
c
-3
-3 d
dλ
2
λ
dλ
λ
c λ-3
1
f
-3
 2 λ




2
dω
2 π df
π df
πf
π λc
 
d -2
λ
dω
2
Fibre monomodali – Dispersione cromatica
Con riferimento alle usuali notazioni nei sistemi lineari, la risposta in fase
di z km di fibra può essere espressa, prescindendo da una inessenziale
fase lineare in frequenza (che origina unicamente un ritardo costante,
senza distorsioni), come
e
1
1

 j   β 2 ω 2   β 3 ω 3  . .  z
6
2

I termini relativi alla fase parabolica e cubica possono essere posti in
relazione ai coefficienti D e S precedentemente determinati, ovvero
β2
λ2
  D
2π c

β 3  2 Dλ  λ
ove c è la velocità della luce nel vuoto.
2
S

λ
2
2π c 2
Fibre monomodali – Dispersione cromatica
D ps/km nm
5
-5
D 
2π c
λ
2
β 2
-10
-15
10
15
20
l = 1.31 mm
l = 1.55 mm
-20
Inoltre, alla lunghezza
d’onda, l0 , di dispersione
nulla (D = 0), si ha
S

2 π c 2

β
λ
4
-25
0.2
0.15
l = 1.55 mm
0.1
3
l = 1.31 mm
0.05
0.02 0.04
0.06 0.08
S ps/km nm2
0.1
Fibre monomodali – Dispersione cromatica e velocità di gruppo
Come esempio, si consideri la seguente situazione, approssimativamente
riferibile a fibre standard con l0 = 1.3 mm.
10
D ps/km - nm
5
1200
-5
-10
500
400
1250
1300
1350
Dvg km/s
1400 300
Dtg ps/km
200
100
-15
-20
1200
Lunghezza d’onda nm
1250 1300 1350 1400
Lunghezza d’onda nm
Fibre monomodali – Dispersione cromatica e banda
Lontano dalla lunghezza d’onda a zero dispersione, la banda della fibra
può essere stimata, in via approssimativa, mediante la consueta relazione
(indeterminazione tempo-frequenza)
B  ΔT  1
 BGbit/s
10 3
10 3


ΔTps
Lkm  D ps/km nm  Δλnm
Alla lunghezza d’onda a zero dispersione, ancora in prima approssimazione,
B  ΔT  1
 BGbit/s
10 3
10 3


2
ΔTps
Lkm  0.5  S ps/km nm 2  Δλnm
Nelle figure seguenti è mostrato l’andamento della banda in funzione della
distanza, per significativi valori di D e S, per tipiche larghezze spettrali di
sorgenti laser, di tipo multimodale, ad esempio Dl = 2 nm, o di tipo DFB
molto avanzati, ad esempio Dl = 0.4 nm.
Prodotti lunghezza-banda maggiori si ottengono modulando esternamente
il laser a semiconduttore (ad esempio, Dl0.1 nm).
Fibre monomodali – Dispersione cromatica e banda
Dl = 2 nm
D = 0,
S = 0.08 ps/km nm2
10
1
D = 20 ps/km nm
D = 3.3 ps/km nm
0.1
5
10
50 100
Lunghezza di tratta L km
500 1000
Fibre monomodali – Dispersione cromatica e banda
Dl = 0.4 nm
D = 0,
S = 0.08 ps/km nm2
10
1
D = 20 ps/km nm
D = 3.3 ps/km nm
0.1
10
100
1000
Lunghezza di tratta L km
10000
Fibre monomodali – Dispersione cromatica e banda
Dl = 0.1 nm
D = 3.3 ps/km nm
10
1
D = 20 ps/km nm
0.1
10
100
1000
Lunghezza di tratta L km
10000
Dispersione 1/L dt/dl ps/km - nm
Fibre monomodali - Dispersione cromatica
Dispersione di
materiale
10
0
Matched, depressed cladding
- 10
Quadrature profile
Triangular profile
- 20
1.1
1.3
1.5
1.7
Lunghezza d’onda mm
Sagomando opportunamente l’indice di rifrazione del core è possibile
modificare la dispersione di guida.
La combinazione con la dispersione di materiale produce dispersioni che
possono essere adattate alle particolari esigenze dei vari tipi di fibra.
Attenuazione dB/km
10
4
16
1
l0
0.4
0.1
- 16
1.1
1.2
1.3
1.4
1.5
Lunghezza d’onda mm
1.6
Dispersione 1/L dt/dl ps/km - nm
Fibre monomodali – Attenuazione e Dispersione cromatica
Fibra monomodale convenzionale step index, matched/depressed cladding
Fibre SM - monomodali a dispersione standard
Sono fibre monomodali ottimizzate in dispersione in seconda finestra,
aventi dispersione cromatica nulla @ 1.31 mm.
A tale lunghezza d’onda, le velocità trasmissive possibili sono elevate,
anche se l’attenuazione è abbastanza alta, circa 0.4 dB/km contro circa 0.2
dB/km in terza finestra, @ 1.55 mm, ove però la dispersione cromatica
elevata presente in tali fibre limita la velocità trasmissiva.
Tuttavia, le caratteristiche globali di attenuazione e dispersione cromatica
delle fibre SM e la relativa economicità della componentistica elettro-ottica
in seconda finestra rendono tali fibre adatte per la rete di accesso e per le
parti della rete di trasporto con esigenze non eccessivamente spinte.
Inoltre, per migliorare le prestazioni di questo tipo di fibra in terza finestra,
in particolare per limitare le attenuazioni dovute alla curvatura del cavo, si
sono realizzate fibre con diametro del core minore rispetto ai valori
standard (9.5 mm contro 10 mm), dette Singolo Modo Reduced, SM – R.
Attenuazione
dB/km
10
Convenzionale step index, depressed cladding
4
16
Dispersion flattened
1
Dispersion shifted
0.4
0.1
- 16
1.1
1.2
1.3
1.4
1.5
Lunghezza d’onda mm
1.6
Dispersione 1/L dt/dl ps/km nm
Fibre monomodali – Attenuazione e Dispersione cromatica
• Fibra convenzionale: step index, matched/depressed cladding;
• Fibra dispersion shifted: profilo d’indice nel core comunemente triangolare,
con minore spot size e maggiore dispersione di guida rispetto al caso step index;
• Fibra dispersion flattened: struttura guidante con più di due cladding (si
ottengono, ad esempio, dispersioni minori di 2 ps/km-nm da 1.3 a 1.6 mm, a spese
di qualche sacrificio sull’attenuazione, ad esempio 0.3 dB/km in terza finestra)
Fibre monomodali – Attenuazione, Dispersione, Amplificazione
0.4
Convenzionale
Dispersion
flattened
Dispersion shifted
16
- 16
Amplificatori in fibra Raman e Amplificatori
a semiconduttore SOA -InGaAsP
0.1
1.1
1.2
1.3
1.4
Lunghezza d’onda mm
60 nm  10.5 THz
1.5
1.6
110 nm  13.75 THz
Dispersione 1/L dt/dl ps/km - nm
1
Amplificatori in fibra Erbio / Raman –
banda C 1530 - 1565 nm
Amplificatori in fibra Erbio / Raman –
banda L 1565 - 1625 nm
4
Amplificatori in fibra Tulio / Raman –
banda S 1460 – 1530 nm
Amp. fibra Praseodimio - banda O -
Attenuazione dB/km
10
Fibre DS - monomodali a dispersione spostata
Le fibre a dispersione spostata hanno una struttura dell’indice di
rifrazione tale da avere lo zero di dispersione cromatica in terza finestra,
@ 1.55 mm, anziché in seconda, @ 1.31 mm, come nelle fibre standard.
La combinazione, in terza finestra, di bassa attenuazione, circa 0.2
dB/km, dispersione cromatica nulla e disponibilità di amplificatori ottici a
fibra attiva (EDFA, Erbium Doped Fibre Amplifier), hanno fatto
preferire tali fibre nella realizzazione di collegamenti a lunga distanza e
grande capacità, attualmente @ 10 Gbit/s.
Però, la dispersione cromatica nulla, vantaggiosa dal punto di vista della
velocità trasmissiva, non lo è dal punto di vista delle interferenze
intercanale in sistemi WDM, Wavelength Division Multiplexing.
Tale fibra ha dovuto, quindi, cedere il passo alle fibre a dispersione non
nulla (fibre NZD, Non-Zero Dispersion).
Fibre NZD (monomodali a dispersione non nulla)
Le fibre a dispersione cromatica non nulla, operanti in terza finestra,
sono state sviluppate per contrastare gli effetti di interferenze
intercanale che si manifestano nei sistemi WDM, Wavelength Division
Multiplexing, sempre operanti in terza finestra, quando si impiegano
per essi le fibre a dispersione spostata, cioè con dispersione cromatica
nulla.
Al contrario, le fibre a dispersione non nulla attualmente posate hanno
valori di dispersione cromatica molti bassi, ma non esattamente nulli, e
risultano pertanto ottime nella realizzazione di sistemi WDM a lunga
distanza e grandissima capacità aggregata (la capacità globale offerta
da tutti i canali), ad esempio 40 canali a 10 Gbit/s.
Fibre ottiche singolo-modo secondo lo standard ITU - T
In ambito ITU - T, le fibre monomodali normalizzate sono:
• ITU T G.652, corrispondente ad una fibra monomodale convenzionale,
con lunghezza d’onda a zero dispersione @ 1.31 mm ;
• ITU T G.653, corrispondente ad una fibra monomodale a dispersione
spostata, con lunghezza d’onda a zero dispersione @ 1.55 mm;
• ITU T G.655, corrispondente ad una fibra monomodale, a dispersione
non nulla in III finestra.
Le fibre ottiche singolo-modo secondo lo standard ITU - T G.652
La fibra G.652 è ottimizzata in seconda finestra (1290 – 1330 nm); la
lunghezza d’onda di dispersione nulla è nell’intorno di 1310 nm (circa 
10 nm); il coefficiente S vale circa 0.09 ps/km - nm2. Conservativamente, è
consigliabile impiegare il valore assoluto di D = 3.3 ps/km-nm in tale
banda.
Conseguentemente, la dispersione in terza finestra (1530 - 1565 nm) è
elevata, D circa 17 ps/km-nm (valore cautelativo 20 ps/km-nm).
L’attenuazione massima è di 0.4 dB/km in seconda finestra, 0.35 dB/km in
terza (tuttavia, con valori tipici nell’intorno di 0.2 dB/km).
E’ economica e di gran lunga la fibra più diffusa a livello mondiale.
L’elevata dispersione la rende immune dal Four Wave Mixing, almeno in
terza finestra, consentendone l’uso con sistemi DWDM. La dispersione
cromatica elevata deve, tuttavia, essere compensata, con elevati bit-rate
(tipicamente, con fibre compensatrici, ad esempio D = - 80 ps/km - nm).
Le fibre ottiche singolo-modo secondo lo standard ITU - T G.653
La fibra G.653 è ottimizzata in terza finestra (1530 - 1565 nm), ove la
dispersione cromatica massima è molto bassa, come mostrato di seguito.
La lunghezza d’onda a dispersione nulla è a 1550  50 nm; il coefficiente
S vale al massimo 0.085 ps/km - nm2; D, in modulo, vale al massimo 3.5
ps/km nm in un intervallo di  25 nm rispetto a 1550 nm.
Conservativamente, è comunque consigliabile, in tale finestra, impiegare il
valore, in modulo, di D = 3.3 ps/km -nm.
L’attenuazione massima è di 0.55 dB/km in seconda finestra, 0.35 dB/km
in terza (tuttavia, con valori tipici nell’intorno di 0.2 dB/km).
E’ una fibra più costosa della G.652 e di gran lunga meno diffusa (Italia,
Giappone, America meridionale).
La sua bassa dispersione la rende esposta agli effetti di Four Wave Mixing.
Una possibilità di utilizzo con sistemi DWDM è l’impiego di una gamma
alta, 1580 - 1600 nm, ove la dispersione non è più così trascurabile.
Le fibre ottiche singolo-modo secondo lo standard ITU - T G.655
E’ una fibra Non Zero Dispersion per la terza finestra (1530 - 1565 nm).
La fibra presenta una dispersione abbastanza modesta, per operare a bit
rate elevati, ma non troppo bassa, così da evitare gli effetti del Four
Wave Mixing, per l’impiego con sistemi DWDM.
E’ una fibra costosa.
6
4
2
1530
-2
1540
1550
1560
-4
-6
Lunghezza d’onda nm
Riguardo ai valori di
dispersione, D, in modulo, ad
esempio, può variare da 0.1
ps/km-nm a 6 ps/km-nm nella
banda 1530 - 1565 nm.
Dispersione di polarizzazione - PMD Polarisation Mode Dispersion
Una potenziale forma di allargamento temporale è causata dalla
birifrangenza delle fibre ottiche.
Piccole asimmetrie nelle geometria trasversale, sforzi indotti
internamente nelle fibre, dovuti al processo di fabbricazione,
perturbazioni meccaniche agenti nel cavo ottico mutano, infatti, la
velocità di propagazione delle due componenti di polarizzazione
ortogonali (birifrangenza, nx  ny), in cui degenera il modo
fondamentale.
Dispersione di polarizzazione - PMD Polarisation Mode Dispersion
Si noti, infatti, che le fluttuazioni temporali, che originano il fenomeno
(dinamico e aleatorio) della dispersione di polarizzazione, sono relative
alle due componenti del modo fondamentale, che mantengono,
comunque, l’ortogonalità reciproca.
Se l’allargamento temporale, che deriva da questo fenomeno, è piccolo,
si ha una riduzione di ampiezza del segnale in decisione, senza
apprezzabile distorsione.
Se tale allargamento temporale è, invece, elevato, le due componenti di
polarizzazione si sovrappongono in tempi “eccessivamente” diversi, con
conseguente distorsione e interferenza intersimbolica in decisione.
Dispersione di polarizzazione
I due stati di polarizzazione ortogonali hanno diverse velocità di gruppo.
Si tratta di un fenomeno aleatorio (accoppiamento aleatorio tra i modi,
indotto da perturbazioni random della birifrangenza lungo la fibra); il ritardo
tra le due polarizzazioni varia con la lunghezza d’onda e col tempo, il suo
valor medio cresce con la radice della lunghezza, Dt = CPMD·L
(l’accoppiamento tra i modi tende ad equalizzare i tempi di propagazione dei
due modi).
Tipicamente, il ritardo medio tra i modi è dell’ordine di 0.1-1 ps/km ,
variabile per uno stesso cavo. Il ritardo differenziale causa interferenza
intersimbolica.
Si tratta di un fenomeno di incerta previsione e difficile correzione; si devono
impiegare fibre e cavi di buona qualità, controllando quelli già installati.
Dispersione di polarizzazione
I valori di dispersione sono normalmente molto modesti, ma, nondimeno,
potrebbero diventare il fattore limitante in sistemi ottici ad altissima
velocità e su lunghe distanze, sia operanti a lunghezze d’onda ove l’altra
dispersione, quella cromatica, è sostanzialmente nulla, sia,
eventualmente, in condizione di compensazione della dispersione
cromatica.
Il limite per questo genere di effetto sui sistemi trasmissivi si può,
semplificativamente, associare ad un Dt  0.1·Tbit (circa 1 dB di
penalità in ricezione) nel caso di impulsi NRZ (Non Return to Zero),
quindi il limite per la velocità di cifra B é
C PMDps/
km
 Lkm 
Tbit, ps
10

BGbit/s 
10 2
C PMDps/
km
 Lkm
Dispersione di polarizzazione
B Gibt/s
La relazione indicata è mostrata di seguito, per tre valori di CPMD .
0.5 ps/km
10
1 ps/km
0.1 ps/km
1
Tipicamente, CPMD
può variare da 0.1
- 0.2 ps/km per le
fibre G.652, e da
0.4 - 0.7 ps/km
per le fibre G.653.
0.1
10
100
1000
10000
L km
Assumendo, come esempio significativo per le fibre attuali, quale valore
massimo 0.5 ps/km, 1 dB di penalità si ha @ 10 Gbit/s su 400 km.
Dispersione di polarizzazione
Se il valor medio del ritardo di gruppo differenziale è 0.1·Tbit, , con una
probabilità di circa 4·10-5 si ha un ritardo di gruppo differenziale massimo
di 0.3·Tbit, .
Tale valore di ritardo può causare una penalità in ricezione (aumento di
potenza minima in ricezione per ottenere la stessa probabilità di errore
ottenibile in assenza di distorsione) di 0.5 - 1 dB, nel caso conservativo che
entrambi gli stati di polarizzazione abbiano la stessa potenza.
Per tale risultato, si fa l’ipotesi di una distribuzione Maxwelliana del
ritardo di gruppo differenziale, lecita ove vi sia un forte e aleatorio
accoppiamento tra le componenti (ortogonali) dello stato di polarizzazione
del modo fondamentale della fibra ottica.
Dispersione di polarizzazione
1
Densità di probabilità del
ritardo di gruppo differenziale,
normalizzato al valor medio.
0.8
p(x)
0.6
0.4
0.2
1
2
x = Dt / Dt
3
4
1
10-1
10-2
10-3
10-4
10-5
10-6

Δτ  32  x

p x 

2

Δτ
π


2
4 x 2

e π
Probabilità di superare il
valore, normalizzato,
dell’ascissa.
0
0.5
1
1.5
2
2.5
3
3.5
Effetti non lineari in fibra
Gli effetti non lineari in fibra stanno diventando sempre più importanti, a
seguito dell’avvento dei sistemi WDM e dell’amplificazione ottica, e del
sempre più elevato bit rate dei canali numerici.
La conseguenza è una crescente potenza ottica in fibra, ciò che produce
effetti non lineari sempre più marcati, che impattano sui sistemi trasmissivi
in modo sempre più rilevante.
Alcune conseguenze di tali non linearità sono positive, quali la possibilità
di generare solitoni, tramite compensazione della dispersione lineare
mediante effetto Kerr, o l’amplificazione ottica per effetto Raman.
Altre conseguenze sono, tuttavia, negative, come l’attenuazione non
lineare, la deformazione dello spettro ottico, l’incremento di disturbi, di
varia origine, sui sistemi trasmissivi.
Effetti non lineari in fibra
Gli effetti non lineari in fibra sono raggruppabili in due categorie: gli
effetti di tipo Kerr e gli effetti dovuti a scatter stimolato.
Gli effetti di tipo Kerr sono causati dalla non linearità dell’indice di
rifrazione della fibra in funzione della potenza ottica, del tipo
P
n  n0  n2 
Aeff
con n0 indice di rifrazione del core a bassi livelli di potenza, n2 coefficiente
di non linearità dell’indice di rifrazione ( 2.2 - 3.4 10-20 m2/W per la silice
drogata), P potenza ottica in fibra (W), Aeff area efficace del core, m2.
Ove non si possa diminuire la potenza ottica in fibra, si possono,
nondimeno, alleviare gli effetti nelle non linearità aumentando Aeff, senza
particolari controindicazioni, strategia oggi perseguita con attenzione.
Effetti non lineari in fibra - Self Phase Modulation
Self Phase Modulation è un fenomeno legato alla dipendenza non
lineare dell’indice di rifrazione nel core con la potenza ottica.
Esso interagisce con la dispersione cromatica della fibra, allargando
temporalmente gli impulsi ottici mentre questi si propagano in fibra.
Da notare che, aumentando la dispersione (aumentando cioè il
coefficiente D (ps/km - nm)) delle fibre ottiche, mentre l’effetto del Four
Wave Mixing si riduce, quello del Self Phase Modulation incrementa, e
viceversa.
In particolare, mentre l’impulso ottico si propaga nella fibra, la parte
iniziale dell’impulso produce un incremento dell’indice di rifrazione (la
potenza ottica aumenta), causando un red shift; analogamente, la parte
finale dell’impulso, fa diminuire l’indice di rifrazione (la potenza ottica
diminuisce), causando un blue shift.
Effetti non lineari in fibra - Self Phase Modulation
Gli shift di frequenza, con conseguenti ed opposti shift delle lunghezze
d’onda, interagiscono con la dispersione delle fibre, per le quali la
velocità di propagazione aumenta con l’aumentare della lunghezza
d’onda se D < 0, oppure diminuisce con la lunghezza d’onda se D > 0.
Tale variazione di velocità in funzione della variazione della lunghezza
d’onda si traduce in allargamenti temporali dell’impulso, di segno
concorde o discorde, rispettivamente, con quelli causati dalla dispersione
cromatica. Se il segno è concorde si possono avere gravi distorsioni del
segnale, se il segno è discorde si possono conseguire miglioramenti sulla
distorsione rispetto alla sola dispersione cromatica.
In particolare, se D > 0, per determinati valori della potenza ottica e della
forma dell’impulso, si può ottenere una esatta compensazione delle
distorsioni, con invarianza della forma dell’impulso nella propagazione
in fibra, da cui la cosiddetta propagazione di solitoni.
Effetti non lineari in fibra - Self Phase Modulation
Gli shift frequenziali detti (o la modulazione di fase impressa all’impulso
durante la propagazione), si possono calcolare, trascurando per tale
valutazione l’attenuazione della fibra, dall’ equazione di Schrödinger
non-lineare
Az, t 
β2  2 Az, t 
2
j
 j γ  Az, t   Az, t 
2
z
2
t
in cui A(z , t) é l’ampiezza dell’impulso ottico (inviluppo complesso), in
funzione della distanza z e del tempo t, g il coefficiente che tiene conto
della non linearità dell’indice di rifrazione (valore tipico 2 W -1 km -1).
Effetti non lineari in fibra - Self Phase Modulation
A partire dall’equazione di Schrödinger non-lineare, ipotizzando che
 A(z, t)2 P0 e –az , ovvero considerando valori medi della potenza, si
ottiene
Az, t 
β2  2 Az, t 
2
j
 j g  Az, t   Az, t  
2
z
2
t
Az, t 
β2  2 Az, t 
-a z
j

j
γ

P
e
 Az, t 
0
2
z
2
t
da cui si ottiene, passando nel dominio della frequenza e assumendo
FA(z, w)= F {A(z, t)} ,
dFA z, ω

dz
 β2 2
-a z 
j  ω  γ  P0 e  FA z, ω
2

Effetti non lineari in fibra - Self Phase Modulation
Integrando la precedente equazione tra o e z e supponendo z>>1, si ottiene
FA z, ω  FA 0,ωe
γ P 
β
j  2 ω2  0  z
a 
 2
da cui si evince che, a seconda del segno di b2 , può essere effettuata una
compensazione più o meno precisa.
In particolare, poiché il termine g·P0 /a è intrinsecamente positivo, la
compensazione è possibile se b2 ha segno negativo, ovvero se D,
coefficiente di dispersione cromatica, ha segno positivo, il che avviene,
di regola, per le lunghezze d’onda superiori a quella ove la dispersione
cromatica è nulla.
Effetti non lineari in fibra - Self Phase Modulation
Nell’ipotesi di un impulso gaussiano di durata T0, a metà altezza, l’effetto
di compensazione può essere messo in relazione con l’allargamento
temporale dell’impulso stesso ad una distanza z (km) dalla sorgente.
Con qualche semplificazione, si ottiene, con riferimento al valore
quadratico medio (normalizzato) dell’impulso rispetto al tempo,
σ
 1
σ0
2
2γP 0β 2 z km
T02
2
 4 γ 2 P02 z km
1

3 3

2
2
 z km
β2

 T4
 0
da cui si evince la possibilità di interazioni concordi o discordi tra Self
Phase Modulation e dispersione cromatica.
Effetti non lineari in fibra - Self Phase Modulation
b2 = -20 ps2/km, T0 = 0.1 ns
2
s/s0
1.5
P0 = 10, 50, 250 mW
1
0.5
10
20
30
40
50
b2 = 20 ps2/km, T0 = 0.1 ns
2
s/s0
1.5
1
P0 = 10, 50, 250 mW
0.5
10
g = 2W-1 km-1
20
km
30
40
50
E’ evidente il meccanismo
di compensazione oppure
di allargamento
temporale, qui applicato a
impulsi gaussiani, in cui
interagiscono la potenza
del segnale ottico, il segno
della dispersione
cromatica e la distanza.
Effetti non lineari in fibra - Four Wave Mixing
La non linearità dell’indice di rifrazione con la potenza ottica causa un
ulteriore fenomeno, noto come Four Wave Mixing.
Se tre campi ottici si propagano in fibra, con frequenza f1 , f2 e f3 , la non
linearità dell’indice di rifrazione origina un quarto campo ottico, con
frequenza f4 , legata alle altre frequenze dalla relazione generale f4 = f1 
f2  f3, ove, almeno in principio, differenti combinazioni dei segni sono
possibili.
In realtà, il fenomeno è significativo se vi è, contemporaneamente,
conservazione della energia (E = hn) e del momento (p = hnn/c).
Con tale condizione, le combinazioni frequenziali del tipo f4 = f1 + f2 - f3
sono le più pericolose, perché per esse la conservazione del momento è
agevole (come facilmente verificabile) se tali canali sono allocati nei
pressi della lunghezza d’onda a zero dispersione, ciò che ha reso critiche
le fibre ITU G.653. Possibile, inoltre, anche la combinazione f4 = 2f1 - f3.
Effetti non lineari in fibra - Four Wave Mixing
Il fenomeno è potenzialmente dannoso per i sistemi WDM, ove genera
crosstalk intercanale, se le frequenze generate cadono sui canali utili.
La situazione più pericolosa è quella ove i canali siano equispaziati. Una
prima contromisura è, quindi, l’impiego di spaziature non uniformi e di
valore opportuno: ciò, tuttavia, può limitare l’efficienza di utilizzazione
della banda disponibile, o appesantire la gestione dei sistemi trasmissivi.
Altrimenti, poiché i disturbi intercanale che, così, si determinano non
sono eliminabili dai canali utili, si deve minimizzarne l’intensità.
Al riguardo, l’efficienza di Four Wave Mixing,  aumenta diminuendo la
spaziatura dei canali e la dispersione cromatica della fibre (D ps/ km nm).
Nel limite di attenuazione nulla (a  0), tale efficienza vale
η

sin 2 π β 2 Δf L
2
2 π
2
2
2
β 2 Δf L
2

2


 Δλ 
 sin c D π L  
 λ 

2
2




 Δλ 
c D π L  
 λ 

2



2
Effetti non lineari in fibra - Four Wave Mixing
Con riferimento al grafico seguente, impiegando una fibra G.652 in III
finestra, D  17 ps/km nm, e il valore della spaziatura ITU di 0.8 nm (100
GHz), l’efficienza di Four Wave Mixing (FWM) è circa -48 dB, con
scarso impatto sulla qualità trasmissiva; molto diversa sarebbe la
situazione impiegando la fibra G.653, con, ad esempio, D <1 ps/km nm.
Spaziatura canali nm
0.5
1
1.5
-10
2
2.5

-20
PFWM
 2 γ  Pch  Leff
Pch
-30
γ  2  3 W 1 km 1
D = 0 ps/km nm
-40
-50
D = 1 ps/km nm
D = 17 ps/km nm
Leff
2η
1

 20 km @0.2 dB/km
α
Effetti non lineari in fibra - Cross Phase Modulation
Cross Phase Modulation è simile a Self Phase Modulation a parte il
fatto che coinvolge più impulsi ottici propaganti, a diverse lunghezze
d’onda, e non un singolo impulso.
In questo fenomeno, i vari impulsi ottici, a causa della loro potenza,
cambiano congiuntamente l’indice di rifrazione in modo non lineare.
Ciò produce una modulazione di fase sui singoli impulsi ottici, dovuta
alla potenza degli altri impulsi, modulazione di fase che la dispersione
della fibra traduce in modulazione di ampiezza (distorsione PM/AM),
e quindi in rumore intercanale tra i vari segnali WDM.
L’effetto è complesso; in generale, a parità di condizione, il rumore
diminuisce all’aumentare della spaziatura frequenziale tra i canali e
in presenza di compensazione della dispersione cromatica.
Nonlinearità in fibra ottica: effetti di scattering
L’altra classe di effetti non lineari è dovuta allo scattering elastico
stimolato, fenomeno per cui i fotoni trasferiscono parte della loro energia
al mezzo non lineare per il tramite di fononi.
Si hanno due fenomeni importanti, entrambi correlati a modi di vibrazione
della silice, lo scattering di Brillouin stimolato e lo scattering di Raman
stimolato.
La fondamentale differenza tra di essi è che nel caso dello scattering di
Brillouin i fotoni interagiscono con fononi acustici, mentre nello
scattering di Raman i fotoni interagiscono con fononi ottici.
Da un punto di vista quantistico, un fotone incidente è annichilito,
generando un fotone ad una frequenza minore (Stokes) e un fonone,
conservando sia l’energia che il momento in tale processo.
Effetti non lineari in fibra - scattering Brillouin stimolato
Lo scattering Brillouin stimolato si origina quando la luce interagisce con
fononi acustici (vibrazioni del materiale), subendo un effetto di diffusione
anelastica (scattering).
La luce diffusa si propaga principalmente in direzione opposta al fascio
principale; inoltre, essa incrementa la sua potenza a spese di quella
originaria (guadagno), che perde progressivamente potenza.
Lo shift di frequenza del segnale diffuso è di circa 11 GHz (0.09 nm), in
una banda assai piccola (DfB circa 20 MHz a 1550 nm), la velocità di
propagazione dell’onda acustica è di 5760 m/s nella silice fusa.
L’effetto, dal punto di vista di interazione tra particelle, può descriversi
imponendo la conservazione dell’energia e del momento complessivo.
Per quanto riguarda l’energia, indicando con i pedici o, s e a le frequenze
del segnale originario, di quello scatterato e del segnale acustico
f0  f s  fa
Effetti non lineari in fibra - scattering Brillouin stimolato
Dal punto vista dei momenti, quello del segnale ottico è proporzionale a
f·n/c, n indice di rifrazione (circa 1.46), mentre quello del fonone acustico
è proporzionale a f/va; si ha quindi, approssimativamente
momento del fonone acustico
momento del fotone (1550 nm)
11 10 9
f


 1.9 10 6 m 1
va
5760
f n
n
1.46
6
1




0.94
10
m
c
λ
1.55 10 6
Il momento del fonone è, quindi, circa uguale al doppio del momento del
fotone; quindi lo scattering, a parte fenomeni spontanei, deve avvenire
all’indietro, tramite la generazione di un segnale ottico di lunghezza
d’onda leggermente maggiore di quello originario, contropropagante
rispetto a quello originario.
Effetti non lineari in fibra - scattering Brillouin stimolato
E’ consuetudine definire come potenza ottica di soglia quella potenza ottica
oltre la quale la potenza retrodiffusa eguaglia quella che si propaga in
avanti nella fibra:
Pth
Aeff  b  Δf 0
 21 
  1 
g B  Leff  Δf B



ove Aeff è l’area efficace del fibra, b è un coefficiente di polarizzazione,
tra 1 e 2 dipendente dalla polarizzazione relativa dei due fasci ottici, gB è
il guadagno del fenomeno, circa 4 10-11 m/W (indipendente da l), Df0 e
DfB le bande del segnale ottico originario e di quello scatterato.
Ne conseguono, per le fibre usuali, modesti valori della potenza di soglia,
dell’ordine dei mW, almeno con laser a riga molto stretta. Inoltre, si ha
rumore di ampiezza, dovuto alla perdita di potenza del segnale utile.
Effetti non lineari in fibra - scattering Brillouin stimolato
Potenza trasmessa
o riflessa dBm
Potenza trasmessa
o riflessa dBm
Potenza iniettata dBm
trasmessa
riflessa
Fibra dispersion shifted,
50 km, l = 1550 nm
Fibra standard, reduced
core, 50 km, l = 1550 nm
trasmessa
riflessa
Effetti non lineari in fibra - scattering Brillouin stimolato
Per evitare gli effetti dello scatter di Brillouin stimolato, si deve:
• mantenere, ove possibile, la potenza ottica in transito sulla fibra sotto il
valore di soglia;
• incrementare la larghezza di riga del laser, ad esempio tramite la
modulazione diretta della sorgente, ciò che può, tuttavia, rendere
intollerabile gli effetti della dispersione cromatica;
• dithering: fare variare, tramite modulazione a bassa frequenza, la
frequenza del laser a semiconduttore; questo procedimento è efficace in
quanto lo scattering di Brillouin stimolato è un processo a banda stretta;
la frequenza modulante deve essere più bassa della frequenza di taglio
inferiore del ricevitore, il quale, così, ignora tale modulazione; la
frequenza di modulazione deve, comunque, essere al massimo dell’ordine
di qualche kHz, per ottenere il risultato desiderato. Lo spostamento di
frequenza della sorgente può essere di parecchie centinaia di MHz.
Effetti non lineari in fibra - scattering Raman stimolato
Lo scattering Raman stimolato consiste nell’interazione tra il segnale
ottico utile e i modi vibrazionali delle molecole della silice (fononi
ottici).
Se un fotone di energia hn interagisce con una molecola che ha una
frequenza di vibrazione fm, la molecola può assorbire una parte
dell’energia del fotone, che è scatterato ad una frequenza minore ns.
Il processo descritto produce luce ad una lunghezza d’onda maggiore di
quella del segnale originario e, se tale lunghezza d’onda è già presente
in fibra, il processo produce amplificazione del segnale a tale lunghezza
d’onda, a spese del segnale utile, che perde progressivamente potenza.
Il fenomeno può essere critico nei sistemi multicanali, ove si manifesta
un trasferimento di potenza dai canali a lunghezze d’onda minori ai
canali a lunghezza d’onda maggiori.
Effetti non lineari in fibra - scattering Raman stimolato
Lo scattering Raman stimolato è un processo a larga banda, indipendente
dalla larghezza di riga della sorgente e dalla modulazione, che può
avvenire in entrambi le direzioni, co-propagante e contro-propagante.
Il trasferimento di potenza verso lunghezze d’onda maggiori può avvenire
in un ampio intervallo di lunghezze d’onda, come mostrato nella figura
seguente, relativa al coefficiente di guadagno del fenomeno.
150 nm
l
Shift di frequenza (THz)
l
Potenze di ingresso e uscita in
un sistema WDM con
scattering Raman stimolato
Effetti non lineari in fibra - scattering Raman stimolato
La frequenza del fonone ottico ha un picco nell’intorno di 13 THz (13 .
10 12 Hz), conseguentemente i momenti di tale fonone e dei fotoni a
1550 nm sono dati, rispettivamente, da
momento del fonone ottico
momento del fotone (1550 nm)
f n
13 1012 1.46
5
1



0.63
10
m
c
3  108

f n
n
1.46
6
1



0.94
10
m
c
λ
1.55 10 6
Poiché il momento del fonone ottico è circa un ordine di grandezza
minore di quello del fotone, la conservazione del momento non pone
particolari restrizioni alla direzione di propagazione dei fotoni scatterati
(Stokes).
Effetti non lineari in fibra - scattering Raman stimolato
Analogamente allo scattering Brillouin, è consuetudine definire potenza
ottica di soglia quella potenza ottica oltre la quale la potenza del segnale
utile è ridotta della metà:
Pth  16 
Aeff
g R  Leff
ove Aeff è l’area efficace del fibra, gR è il guadagno del fenomeno, circa
10-13 m/W , contro il guadagno Brillouin, gB circa 4 10-11 m/W, con
potenze di soglia dell’ordine, quindi, delle centinaia di mW, contro quelle
dei mW dovute a scattering Brillouin (con laser a semiconduttore a riga
molto stretta).
Poiché, tipicamente, la potenza trasmessa in fibra è dell’ordine delle
decine di mW, lo scattering Ramam stimolato non contribuisce
all’attenuazione della fibra.
Effetti non lineari in fibra - scattering Raman stimolato
Sebbene lo scattering Raman non costituisca un fattore limitante per
sistemi a singolo canale, a causa della sua alta soglia (circa 500 mW @
1550 nm), la situazione è differente nei sistemi WDM, ove l’effetto
Raman amplifica i canali a lunghezze d’onda maggiore a spese di quelli
a lunghezza d’onda minore, nell’ambito della banda del fenomeno.
Tale trasferimento di potenza da luogo, di fatto, a crosstalk intercanale;
esso può essere evitato solo se l’amplificazione Raman è trascurabile
sulla tratta in fibra (ad esempio, se la perdita di potenza sul generico
canale a vantaggio di tutti gli altri è di pochi percento della potenza utile:
la potenza massima per canale, allora, decresce tipicamente, in III
finestra, dal centinaio di mW @ 10 canali WDM a circa 1 mW @ 100
canali WDM, in modo circa inverso al quadrato del numero dei canali
WDM).
Lo scattering Raman è, comunque, utilizzabile proficuamente per
l’amplificazione ottica, traendo giovamento dalla banda elevata del
fenomeno (circa 10 THz) e dalla possibilità di amplificazione distribuita.
Effetti non lineari in fibra - scattering Raman stimolato
L’amplificazione per effetto Raman non richiede un drogaggio
particolare per le fibre ottiche.
Ad essa ci si riferisce usualmente come amplificazione distribuita, nel
senso che tale amplificazione si attua lungo tutta la fibra impiegata per
la trasmissione, invece di concentrare l’amplificazione in punti definiti
(con conseguenze negative sul rumore e sugli effetti non lineari in fibra).
In sostanza, la stessa fibra che trasporta il segnale utile può trasportare
un altro segnale ottico (pompa), a lunghezza d’onda inferiore di circa
100 nm, il quale può amplificare il segnale utile, tramite effetto Raman,
lungo la fibra.
Migliori prestazioni si hanno iniettando la pompa sia in ingresso sia in
uscita dalla fibra; inoltre, più segnali di pompa, a lunghezze d’onda
diverse, possono essere usati per amplificare un insieme di segnali ottici.
Cavi ottici
I cavi ottici sono, in generale, costituiti:
• da un insieme di fibre ottiche, disposte nel nucleo ottico, protette da
stress meccanici e da infiltrazioni di umidità;
• da un elemento centrale, cilindrico, dielettrico o in acciaio, per
conferire al cavo le necessarie proprietà di elasticità e dilatazione
termica;
• da una tamponatura, o da simili protezioni, contro l’ingresso
longitudinale di acqua;
• da armature di filati aramidici, per assorbire gli sforzi di trazione,
durante la posa del cavo, senza danno per le fibre;
• da ulteriori strati di nastri o fili di acciaio, per la protezione contro
roditori e umidità, saldati alla guaina esterna di polietilene.
Cavi ottici
Le protezioni delle fibre nel cavo sono, al solito, di tipo aderente o lasco.
Riguardo al tipo aderente, di attuale e particolare interesse le strutture a
nastro, ciascuno dei quali contenente ad esempio 4 fibre ottiche, nastri a
loro volta alloggiati in strutture a cave nel nucleo ottico; tali strutture a
nastro offrono maggiore compattezza nel cavo e la preziosa possibilità di
giunzione multipla, con sensibili vantaggi operativi.
Riguardo al tipo lasco, le fibre sono alloggiate liberamente dentro tubetti
plastici, ad esempio 12 fibre per tubetto, o entro scanalature scavate in
un tondino di polietilene; tubetti e cave sono tamponati, onde impedire la
propagazione longitudinale dell’acqua; le fibre, così protette, sono quindi
cordate assieme e fasciate, costituendo più gruppi attorno al nucleo.
Le fibre attualmente posate sono di tipo monomodo a dispersione non
spostata, per la rete di accesso e di trasporto, e di tipo monomodo a
dispersione non nulla, per la rete di trasporto.
Cavi ottici
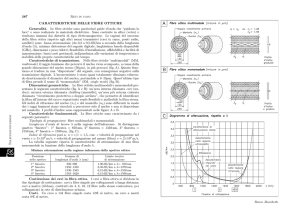
Cavi ottici
Cavi ottici - struttura a nastri
Guaina esterna
1100 mm
Nastro d’acciaio corrugato
Filati aramidici
Tamponante
Struttura scanalata
Elemento centrale dielettrico
Nastro da 4 fibre (5 nastri)
Fasciatura
Cavo per la rete di accesso e trasporto con fibre monomodali G.652 a
dispersione non spostata, da 20/40/60/100 fibre ottiche, a nastri da 4 fibre
Cavi ottici - struttura a tubetti
Guaina esterna
Nastro d’acciaio corrugato
Filati aramidici o di vetro
Elemento centrale dielettrico
Tamponante
8 Tubetti tamponati
con 12 fibre ottiche
Cavo per la rete di trasporto con fibre monomodali G.655 a dispersione
non nulla, da 96 fibre ottiche, a tubetti di 12 fibre.