Document

Dal teorema di Carnot al teorema di
Clausius
1
•
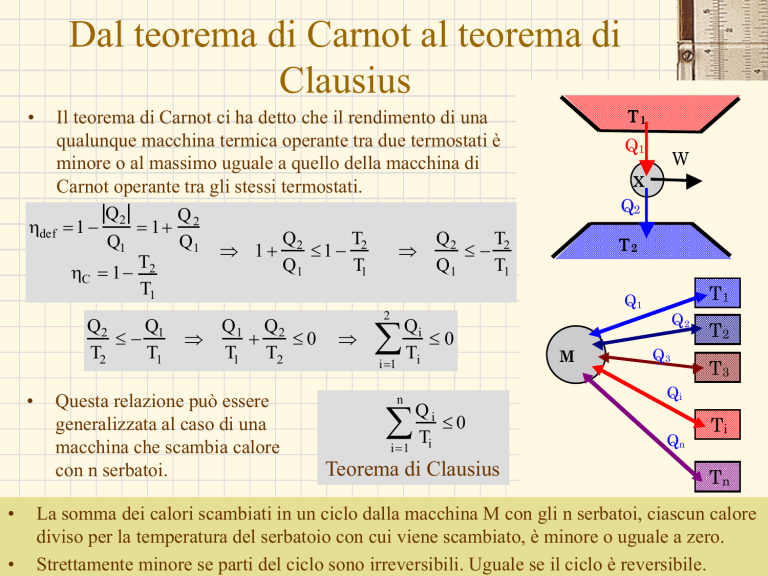
Il teorema di Carnot ci ha detto che il rendimento di una
qualunque macchina termica operante tra due termostati è
minore o al massimo uguale a quello della macchina di
Carnot operante tra gli stessi termostati.
Q
Q
def  1  2  1 2
Q2
T
Q1
Q1  1  Q2  1  T2

 2
T
Q1
T1
Q1
T1
C  1 2
T1
Q2
Q
 1
T2
T1
•
•
•
Q1 Q2


0
T1 T2
Questa relazione può essere
generalizzata al caso di una
macchina che scambia calore
con n serbatoi.
2


i1
Qi
0
Ti
n

i1
Q1
W
X
Q2
2
T1
Q1
M
Q2
Q3
T2
T3
Qi
Qi
0
Ti
Teorema di Clausius
Qn
Ti
Tn
La somma dei calori scambiati in un ciclo dalla macchina M con gli n serbatoi, ciascun calore
diviso per la temperatura del serbatoio con cui viene scambiato, è minore o uguale a zero.
- Edile A 2002/03
Strettamente minore se parti del ciclo sono irreversibili. Uguale se il ciclo è G.M.
reversibile.
Il teorema di Clausius
n
•
•
•
•
Qi è il calore scambiato con il serbatoio i-esimo
Ti è la temperatura del serbatoio i-esimo
La somma è effettata su tutti i serbatoi con cui
viene scambiato calore in un ciclo
Se il numero di serbatoi con cui il sistema
interagisce in un ciclo è infinito:

Q
0
T
•
•

i1
Qi
0
Ti
T1
Q1
M
Q2
Q3
T2
T3
Qi
Strettamente minore = ciclo irreversibile
Uguale = ciclo reversibile
Qn
Ti
Tn
•
•
Q è il calore infinitesimo scambiato con il serbatoio a temperatura T
T è la temperatura del serbatoio con cui viene scambiato il calore Q.
– N.B. la temperatura del sistema quando viene scambiato il calore Q potrebbe non
essere nota
– Solo se la trasformazione è reversibile la temperatura del sistema quando viene
scambiato il calore Q è proprio uguale alla temperatura T del serbatoio con cui
avviene lo scambio
•
L’integrale è esteso al ciclo
G.M. - Edile A 2002/03
L’entropia
•
•
•
Consideriamo due trasformazioni reversibili R1 ed R2
che portano il sistema dallo stesso stato iniziale allo
stesso stato finale
L’insieme della prima trasformazione più la seconda
percorsa al contrario costituiscono un ciclo
reversibile.
Applicando Clausius a questo ciclo abbiamo:

C

R2
•
0
perchè
il ciclo
dQ R calore
è rescam biat o
versibil e
reversibilm ent e
i
f
Q R
T
Q R

T

R2
i
f
Q R
T


f
i
R1
Q R

T
Da cui si ottiene:
P
R1
f
i
R2
i
Q R
0
T

f

f
R2
i
R1
Q R

T

V
f
i
R2
Q R
T
Questa eguaglianza vale per qualunque trasformazione che connette lo stato
iniziale con lo stato finale: l’integrale del calore scambiato reversibilmente
diviso per la temperatura a cui avviene lo scambio, non dipende dalla
G.M. - Edile A 2002/03
trasformazione ma solo dallo stato iniziale e finale
L’entropia
•
Esiste dunque una funzione di stato che chiameremo entropia, S, tale che
l’integrale del calore scambiato reversibilmente diviso per la temperatura a
cui avviene lo scambio, effettuato su una trasformazione reversibile che
connette lo stato iniziale i e lo stato finale f, è dato dalla differenza dei valori
della funzione S nello stato finale meno quello dello stato iniziale

f
i
Q R
 Sf  Si
T
Sf  Si  S
R
•
•
Essendo S una funzione di stato, quando un sistema passa dallo stato iniziale i
allo stato finale f, la variazione di entropia è sempre la stessa qualunque sia la
trasformazione utilizzata (reversibile o irreversibile).
Naturalmente per determinare la variazione di entropia devo calcolarla
applicando la definizione: il calcolo della variazione di entropia si può fare
solo su una trasformazione reversibile.
– Se la trasformazione che stiamo studiando è reversibile allora non c’è problema,
basta applicare la definizione alla trasformazione.
– Se invece la trasformazione è irreversibile, occorre innanzitutto sostituire la
trasformazione data con una reversibile che fa passare il sistema dallo stesso stato
iniziale allo stesso stato finale, poi applicare la definizione.
G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
serbatoio di calore
•
•
•
•
Durante il trasferimento di calore
il serbatoio non cambia stato
Rimane in uno stato di equilibrio
termodinamico
Il trasferimento di calore avviene
In maniera reversibile
T
Q
S 

i
f
Q R 1 f
Q

Q R 
T
T i
T

G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
Trasformazione reversibile
•
•
Durante il trasferimento di calore
il serbatoio e il sistema hanno la
stessa temperatura
Considerando un tratto infinitesimo
di trasformazione
dSsist 
Q
T
T
Q
Sistema
T
dSserb 
Q
dSUn iverso  dSSistema  dSSerbato io
T
QR QR


0
T
T
G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
generica trasformazione di un gas perfetto
P
•
•
Consideriamo una generica trasformazione if
Poiché l’entropia è una funzione di stato, per il
calcolo della sua variazione possiamo utilizzare una
qualunque trasformazione come quella mostrata in
figura.
f
S 

i
Q R

T
c


i
f
dT
nC V

T


c
c
i
QR

T
f

c
QR

T
c

i
c
Pf
Pi
f
i
f
i
f
nC VdT

T
c

c
nRT dV

T V
Vi
Vf
V
f
dV
T
V
 
 
nR
 nC V lnT  nR lnV  nC V ln c  nR ln f 
V
 i
 c
Ti
Vc
T
V
 nC V ln f  nR ln f
Ti
Vi
Tf
V
 nR ln f
Ti
Vi
T
P
S  nCP ln f  nR ln f
Ti
Pi
P
V
S  nCV ln f  nCp ln f
Pi - Edile A 2002/03
Vi
G.M.
S  nCV ln
Calcolo della variazione di entropia in alcune trasformazioni:
cambiamento di fase
•
Durante un cambiamento di fase, la temperatura rimane costante:
S  Sliq  Ssol
QR
1


sol Tfusion e la temperaturaTfusion e

liq
di fusio ne è
costante

liq
m fusion e
Q R 
Tfusion e
sol
G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
espansione libera
•
•
•
•
Vuoto
Gas
L’espansione libera è una
trasformazione irreversibile
Per calcolo la variazione
fig. A
dell’entropia dobbiamo
• Vi,T
utilizzare trasformazione
reversibile
P
Per esempio una trasformazione
Pi
isoterma
dU  Q  W
Sull’isoterma
dU  0  Q  W
f
Ssist 

i
QR

T
Samb  0
f

i
QR

T
Pe
•
Vf,T
i
Pf
f

f

i
nRT dV
Vf
 nRln
T V
Vi
Vi
Vf
V
Suniv  Ssist  Samb  0
G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
conduzione di calore
•
•
•
•
•
•
Consideriamo due corpi a temperatura diversa T1 e T2.
Se i due corpi interagiscono solo tra di loro il calore
Corpo 2 Corpo 1
ceduto dal corpo 1 sarà assorbito dal corpo 2
T2
T1
La trasformazione è irreversibile
T1>T2
Ma avviene a pressione costante
Il calore trasferito da un corpo all’altro può essere
Q1  m1c1Tm  T1   0
calcolato come se la trasformazione fosse reversibile
Q2  m 2 c2 Tm  T2   0
Diciamo Tm la temperatura di equilibrio
m c T  m 2 c 2T2
Q2  Q1  m2c2 Tm  T2  m1c1Tm  T1 
Tm  1 1 1
m 1c1  m 2c 2
f
S2 

i
f
S1 

i
QR

T
QR

T
f

i
f

i
m 2c 2dT
T
 m2 c 2ln m
T
T2
m 1c1dT
T
 m1c1ln m
T
T1
T
T
S  S1  S2  m1c1ln m  m 2c 2ln m
T1
T2
Q
T+dT
Corpo 2
T
G.M. - Edile A 2002/03
Calcolo della variazione di entropia in alcune trasformazioni:
conduzione di calore
•
Se i due corpi sono della stessa sostanza ed hanno la
stessa massa
c c c
1
Corpo 2 Corpo 1
2
T2
m1  m2  m
m1c1T1  m 2 c 2T2 mc T1  T2  T1  T2 
Tm 


m 1c1  m 2c 2
2mc
2
S  S1  S2  m1c1ln
T1>T2
Tm
T
 m 2c 2ln m 
T1
T2
T+dT
Q
2
 Tm
T

T
 mc ln
 ln m  mc ln m
 T1
T2 
T1T2
T1  T2 
T1
Corpo 2
T
2
2
Tm
T1T2


4
T1T2

T12  2T1T2  T 22
4T1T2
T12  2T1T2  T 22  4T1T2
4T1T2

T12  2T1T2  T22  4T1T2  4T1T2
4T1T2
T  T2 
1 1

2
4T1T2
1
S  Suni  0
G.M. - Edile A 2002/03
L’aumento dell’entropia nelle
trasformazioni naturali
•
•
•
Vogliamo dimostrare che nelle trasformazioni naturali
(irreversibili), l’entropia dell’universo termodinamico (ossia
del sistema più quella dei serbatoi di calore con cui esso
interagisce) aumenta.
In altri termini: la variazione di entropia dell’universo
termodinamico è sempre maggiore di zero (è uguale a zero
solo per trasformazioni reversibili).
L’insieme della trasformazione irreversibile I e di quella
reversibile II percorsa al contrario costituisce un ciclo
– Applichiamo la disuguaglianza di Clausius

Q

T
f

i,I
Q

T
i

Q rev

T
f, II
f

i, I
Q

T
f
Ssist 

i, I
f

i, II
P
II
I
V

Q
0
T
f
Qrev
Q

 Ssist  0
T
T

i,I
Q
T
G.M. - Edile A 2002/03
L’aumento dell’entropia nelle
trasformazioni naturali
•
Se durante la trasformazione irreversibile il sistema non
scambia calore con l’ambiente (sistema isolato), allora:
f

i,I
Q
0
T
•
•
•
•
Ssist 

i, I
Q
T
 Ssist  0  Suniv  Ssist  Samb  0
0
Samb  0
•
f
0
Se durante la trasformazione irreversibile viene scambiato del
calore tra sistema e ambiente esterno
Si ridefinisce un sistema più ampio costituito dal sistema stesso
più tutte le sorgenti con cui il sistema ha interagito
Il sistema più ampio coincide con l’universo termodinamico
Tale sistema è isolato, tutti gli scambi di calore avvengono al
suo interno.
Ripetendo il ragionamento già fatto per questo sistema più
ampio (isolato) otterremo:
S
0
Sistema
più ampio
T1
Sistema
T2
Tn
sist _ amp io
 Suniv
G.M. - Edile A 2002/03
Entropia ed energia inutilizzabile
•
Nei processi naturali l’entropia dell’universo aumenta
– Pendolo che si ferma per gli attriti
•
Contemporaneamente si perde capacità di trasformare l’energia in lavoro
meccanico
– Nel caso del pendolo, il secondo principio della termodinamica ci impedisce di
estrarre l’energia dall’aria e ritrasformarla tutta in energia meccanica.
•
In una trasformazione irreversibile, l’energia diventata inutilizzabile per essere
trasformata in lavoro meccanico è data da:
Ein=SunivTo
•
•
•
To è la temperatura del serbatoio a più bassa temperatura tra quelli utilizzati
durante la trasformazione.
Suniv è la variazione di entropia dell’universo
N.B. non si deve pensare che l’energia non si sia conservata, solo che ha perso
la capacità di essere trasformata in energia meccanica
– È come quando si rompe un bicchiere: nessuno dei pezzi del bicchiere viene perso, il
bicchiere perde solo la sua forma e quindi la capacità di contenere dei liquidi.
G.M. - Edile A 2002/03
•
Una mole di gas perfetto che occupa un volume V1=12.3 litri alla temperatura
T1=300 K subisce una espansione libera che lo porta a raddoppiare il suo volume,
V2=24.6 litri. Il gas viene quindi riportato con una trasformazione reversibile nel
suo stato iniziale.
– Qual è la variazione di entropia dell’universo sull’intero ciclo?
– Descrivere quale trasformazione reversibile voi usereste per riportare il gas al suo stato
iniziale dopo l’espansione libera.
– Calcolare quanta energia durante il ciclo si è trasformata in energia non più convertibile
in lavoro.
– Verificare che essa è pari a T1S.
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
•
Un pezzo di 50.0 g di rame alla temperatura di 400 K viene posto in una scatola
isolante insieme a un pezzo di 100 g di piombo alla temperatura di 200 K.
– Qual è la temperatura di equilibrio dei due pezzi di metallo?
– Qual è la variazione di energia interna del sistema costituito dai due pezzi di metallo, tra
lo stato di equilibrio finale e lo stato iniziale?
– Qual è la variazione di entropia del sistema?
– (calori specifici: piombo 129 J/(kg K), rame 387 J/(kg K))
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
•
Alla pressione atmosferica l’etanolo bolle alla temperatura di 78°C, congela a –114
°C e possiede un calore latente di evaporazione di 879 kJ/kg, un calore latente di
fusione di 109 kJ/kg e un calore specifico di 2.43 kJ/(kg K).
– Quanto calore deve cedere un campione di massa 0,510 kg, inizialmente in fase
aeriforme alla temperatura di 78°C, per diventare solido alla temperatura di –114 °C?
– Qual è la variazione di entropia subita dal campione in questo processo?
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
•
In un cilindro, munito di un pistone a tenuta, sono contenuti 20 grammi di idrogeno
(molecola H2, massa molecolare M=2 u) alla pressione atmosferica (1.01x105 Pa).
Il gas viene riscaldato a pressione costante dalla temperatura di 30 °C alla
temperatura di 40°C, tenendolo a contatto con un serbatoio di calore alla
temperatura di 50°C.
Appli
cazio
ne
– Supponendo che durante la trasformazione il gas si comporti come un gas perfetto,
determinare:
– Il numero di moli.
– Il lavoro fatto dal gas.
– La variazione di energia interna.
Pe=1atm
– La variazione di entropia del gas e dell’universo.
•
O

50°C
G.M. - Edile A 2002/03
•
Un litro di gas con g=1.3 inizialmente è in equilibrio termico a 273 K di
temperatura e a 1.0 atmosfera di pressione. Esso viene compresso adiabaticamente
a metà del suo volume originario.
– Trovate la sua pressione e la sua temperatura finali.
– Successivamente il gas viene raffreddato lasciando disperdere, a pressione costante, il
calore nell’ambiente esterno e fino a riportarlo alla temperatura dell’ambiente, 273 K,
Qual è il suo volume finale.
– Calcolare la variazione di entropia del sistema e dell’ambiente esterno nelle due
trasformazioni.
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
•
Un impianto a carbone da 1000 MW opera tra 800 e 300 K con un rendimento pari
a due terzi del massimo possibile. Con che ritmo si perde il calore prodotto?
Supponiamo che si usi l’acqua per eliminare il calore in eccesso e, in questo modo
il liquido si riscalda di 8 °C. Quanta acqua deve fluire al secondo attraverso
l’impianto. Di quanto aumenta l’ entropia dell’universo in un secondo?
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
• Si pone un cubo di ghiaccio di 12.6 g, alla temperatura di 0 °C, in un
lago alla temperatura di 15 °C. Si determini la variazione di entropia
dell'universo quando il ghiaccio si porta all'equilibrio termico con il lago
(si assuma il calore latente di fusione del ghiaccio pari a f=333 kJ/kg, il
calore specifico dell'acqua pari a c =1 cal/(g K))
•
Appli
cazio
ne
O
G.M. - Edile A 2002/03
• Cinquanta grammi di ossigeno gassoso a 320 K compiono 80 J di lavoro
mentre viene assorbita una quantità di calore di 40 cal.
• )Qual è la variazione di energia interna?
• )La variazione di temperatura?
• )La variazione di entropia considerando la trasformazione isobara?
Appli
cazio
ne
• (L'ossigeno è biatomico con peso atomico 16. 1 cal = 4.186 J)
•
O
G.M. - Edile A 2002/03
• Una macchina frigorifera di coefficiente di prestazione 3 mantiene a
temperatura costante T1 =250 K in una cella frigorifera, scaricando il
calore nell'ambiente esterno, a temperatura di 300 K. Il motore della
macchina, posto all'esterno, trasforma in lavoro utile il 90%
dell'energia assorbita dalla rete elettrica. Il rimanente 10% viene
dissipato in calore.
• L'isolamento delle pareti che separano la cella frigorifera
dall'ambiente esterno è tale che ogni ora essa assorbe una quantità di
calore Q1=4,2 x 107 J che deve essere sottratta per mantenere
costante la sua temperatura T1.
• Si domanda:
•
O
Appli
cazio
ne
• ) la potenza utile fornita dal motore e quella assorbita dalla rete;
• il calore complessivo scaricato all'esterno in un'ora;
• ) la variazione di entropia, dopo un'ora, della cella frigorifera e dell'ambiente
esterno;
• ) La potenza che il motore assorbirebbe dalla rete, se il frigorifero funzionasse
da macchina di Carnot reversibile, ed il calore scaricato all'esterno in un'ora.
G.M. - Edile A 2002/03