Document

Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
STUDENTE:
MATRICOLA:
a 0
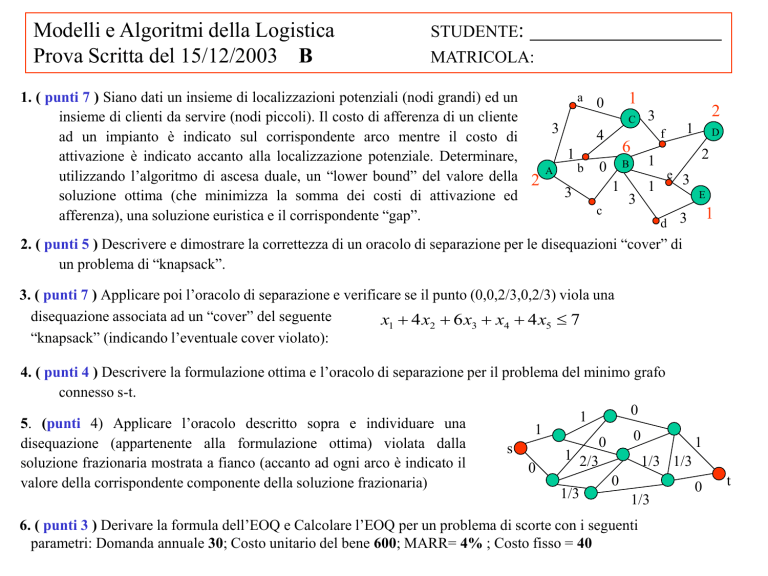
1. ( punti 7 ) Siano dati un insieme di localizzazioni potenziali (nodi grandi) ed un
1
2
insieme di clienti da servire (nodi piccoli). Il costo di afferenza di un cliente
C 3
3
1 D
f
4
ad un impianto è indicato sul corrispondente arco mentre il costo di
6
1
2
attivazione è indicato accanto alla localizzazione potenziale. Determinare,
1
b 0 B
A
e 3
utilizzando l’algoritmo di ascesa duale, un “lower bound” del valore della 2
1
1
3
E
soluzione ottima (che minimizza la somma dei costi di attivazione ed
3
c
1
afferenza), una soluzione euristica e il corrispondente “gap”.
d 3
2. ( punti 5 ) Descrivere e dimostrare la correttezza di un oracolo di separazione per le disequazioni “cover” di
un problema di “knapsack”.
3. ( punti 7 ) Applicare poi l’oracolo di separazione e verificare se il punto (0,0,2/3,0,2/3) viola una
disequazione associata ad un “cover” del seguente
x1  4 x2  6 x3  x4  4 x5  7
“knapsack” (indicando l’eventuale cover violato):
4. ( punti 4 ) Descrivere la formulazione ottima e l’oracolo di separazione per il problema del minimo grafo
connesso s-t.
0
1
5. (punti 4) Applicare l’oracolo descritto sopra e individuare una
1
0
0
1
disequazione (appartenente alla formulazione ottima) violata dalla
s
1 2/3
1/3 1/3
soluzione frazionaria mostrata a fianco (accanto ad ogni arco è indicato il
0
0
valore della corrispondente componente della soluzione frazionaria)
0
1/3
1/3
6. ( punti 3 ) Derivare la formula dell’EOQ e Calcolare l’EOQ per un problema di scorte con i seguenti
parametri: Domanda annuale 30; Costo unitario del bene 600; MARR= 4% ; Costo fisso = 40
t
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
a 0
1. ( punti 7 ) Siano dati un insieme di localizzazioni potenziali (nodi grandi) ed un
1
2
insieme di clienti da servire (nodi piccoli). Il costo di afferenza di un cliente
C 3
3
1 D
f
4
ad un impianto è indicato sul corrispondente arco mentre il costo di
6
1
2
attivazione è indicato accanto alla localizzazione potenziale. Determinare,
1
b 0 B
A
e 3
utilizzando l’algoritmo di ascesa duale, un “lower bound” del valore della 2
1
1
3
E
soluzione ottima (che minimizza la somma dei costi di attivazione ed
3
c
1
afferenza), una soluzione euristica e il corrispondente “gap”.
d 3
SOLUZIONE
1. Definisco i costi (afferenza e attivazione)
A
B
C
D
E
a
3
∞
0
∞
∞
b
1
0
4
∞
∞
c
3
1
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
2
6
1
2
1
Costi di afferenza [c]
Costi di attivazione [f]
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
2. Calcolo i vettori  e 
3. Calcolo Vk/|m(k)|
A
B
C
D
E

a
3
∞
0
∞
∞
3
b
1
0
4
∞
∞
1
c
3
1
∞
∞
∞
2
d
∞
3
∞
∞
3
∞
e
∞
1
∞
2
3
1
f
∞
1
3
1
∞
2

2
6
1
2
1/1=1
1/1=1
2/1=2
1/2
1/1=1
2/2=1
1
4. Massimo in corrispondenza della riga c.
Incremento di Vc le u corrispondenti ai
minimi della riga c (uno solo!)
A
B
C
D
E
a
3
∞
0
∞
∞
b
1
0
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
5. Aggiorno i vettori  e 
6. Aggiorno Vk/|m(k)|
A
B
C
D
E

a
3
∞
0
∞
∞
3
b
1
0
4
∞
∞
1
c
3
1+2
∞
∞
∞
∞
d
∞
3
∞
∞
3
∞
e
∞
1
∞
2
3
1
f
∞
1
3
1
∞
2

2
4
1
2
1/1=1
1/1=1
2/2=1
1/2
1/1=1
2/2=1
1
7. Massimo in corrispondenza della riga a.
Incremento di Va le u corrispondenti ai
minimi della riga a (uno solo)
A
B
C
D
E
a
3
∞
0+1
∞
∞
b
1
0
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
8. Aggiorno i vettori  e 
9. Aggiorno Vk/|m(k)|
A
B
C
D
E

a
3
∞
0+1
∞
∞
2
b
1
0
4
∞
∞
1
c
3
1+2
∞
∞
∞
∞
d
∞
3
∞
∞
3
∞
e
∞
1
∞
2
3
1
f
∞
1
3
1
∞
2

2
4
0
2
0/1=0
1/1=1
2/2=1
1/2
1/1=1
2/2=1
1
10. Massimo in corrispondenza della riga b.
Incremento di Vb le u corrispondenti ai
minimi della riga b (uno solo)
A
B
C
D
E
a
3
∞
0+1
∞
∞
b
1
0+1
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
11. Aggiorno i vettori  e 
12. Aggiorno Vk/|m(k)|
A
B
C
D
E

a
3
∞
0+1
∞
∞
2
b
1
0+1
4
∞
∞
3
c
3
1+2
∞
∞
∞
∞
d
∞
3
∞
∞
3
∞
e
∞
1
∞
2
3
1
f
∞
1
3
1
∞
2

2
3
0
2
0/1=0
2/2=1
2/2=1
1/2
1/1=1
2/2=1
1
13. Massimo in corrispondenza della riga b.
Incremento di Vb le u corrispondenti ai
minimi della riga b (due)
A
B
C
D
E
a
3
∞
0+1
∞
∞
b
1+2
0+1+2
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
14. Aggiorno i vettori  e 
15. Aggiorno Vk/|m(k)|
A
B
C
D
E

a
3
∞
0+1
∞
∞
2
b
1+2
0+1+2
4
∞
∞
1
c
3
1+2
∞
∞
∞
∞
d
∞
3
∞
∞
3
∞
e
∞
1
∞
2
3
1
f
∞
1
3
1
∞
2
0
1

0
2
0/1=0
0/2=0
0/2=0
1/2
1/1=1
1/2
1
16. Massimo in corrispondenza della riga e.
Incremento di Ve le u corrispondenti ai
minimi della riga e (uno solo)
A
B
C
D
E
a
3
∞
0+1
∞
∞
b
1+2
0+1+2
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1+1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
17. Aggiorno i vettori  e 
18. Aggiorno Vk/|m(k)|
A
B
C
D
E

a
3
∞
0+1
∞
∞
2
b
1+2
0+1+2
4
∞
∞
1
c
3
1+2
∞
∞
∞
∞
d
∞
3
∞
∞
3
∞
e
∞
1+1
∞
2
3
1
f
∞
1
3
1
∞
2
0
0

0
2
0/1=0
0/2=0
0/2=0
0/2=0
0/1=0
0/2=0
1
19. Tutte le righe sono bloccate. L’algoritmo
si arresta.
A
B
C
D
E
a
3
∞
0+1
∞
∞
b
1+2
0+1+2
4
∞
∞
c
3
1+2
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1+1
∞
2
3
f
∞
1
3
1
∞
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 1
20. Calcolo del vettore z (minimi di riga della matrice aggiornata)
A
B
C
D
E
z
a
3
∞
0+1
∞
∞
1
b
1+2
0+1+2
4
∞
∞
3
c
3
1+2
∞
∞
∞
3
d
∞
3
∞
∞
3
3
e
∞
1+1
∞
2
3
2
f
∞
1
3
1
∞
1

0
0
2
0
LB=13
UB=Z({A,B,C})=9+6=15
1
A
B
C
D
E
a
3
∞
0
∞
∞
b
1
0
4
∞
∞
c
3
1
∞
∞
∞
d
∞
3
∞
∞
3
e
∞
1
∞
2
3
f
∞
1
3
1
∞
2
6
1
2
1
“gap”=15-13 = 2
Osservazione: A è inutile e può
essere eliminato. In tal caso, la
Soluzione diviene {B,C}, UB=13 e
il “gap”=0
Valutazione Esercizio 1:
-2 punti: se non viene scritta in modo corretto la matrice dei costi (con ∞ al posto giusto)
-2 punti: se non viene calcolato l’UB come nelle pagine precedenti
-2 punti: per errori nell’applicazione dell’algoritmo
• Ignorata la soluzione euristica calcolata con il “greedy” o con altro metodo
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003
B
SOLUZIONE ESERCIZIO 2
2. ( punti 5 ) Descrivere e dimostrare la correttezza di un oracolo di separazione per le disequazioni “cover” di
un problema di “knapsack”.
La dimostrazione è quella riportata nelle pagine 7,8 e 9 della Lezione 9
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 3
3. ( punti 7 ) Applicare poi l’oracolo di separazione e verificare se il punto (0,0,2/3,0,2/3) viola una
disequazione associata ad un “cover” del seguente
x1  4 x2  6 x3  x4  4 x5  7
“knapsack” (indicando l’eventuale cover violato):
Risposta:
1. Definire il “knapsack” duale per la separazione approssimata:
max (x*1 -1) u1 +(x*2 -1) u2 +(x*3 -1) u3 + (x*4 -1) u4 + (x*5 -1) u5
u1 + 4u2 + 6u3 + u4 + 4u5 > 8
max (0-1) u1 +(0-1) u2 +(2/3 -1) u3 + (0-1) u4 + (2/3 -1) u5
u1 + 4u2 + 6u3 + u4 + 4u5 > 8
max -u1 -u2 -1/3u3 -u4 -1/3 u5  min u1 + u2 + 1/3u3 + u4 + 1/3 u5
u1 + 4u2 + 6u3 + u4 + 4u5 > 8
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 3
2. Ordinamento delle variabili (rapporti valore/ingombro crescenti)
max -u1 -u2 -1/3u3 -u4 -1/3 u5  min u1 + u2 + 1/3u3 + u4 + 1/3 u5
u1 + 4u2 + 6u3 + u4 + 4u5 > 8
u1
u2
u3
u4
1
1/4
1/18 1
u5
u3
u5
u2
1/12
1/18 1/12 1/4
u1
u4
1
1
ordinamento
3. Soluzione del “knapsack duale”
u3
u5
u2
u1
u4
1
1/2
0
0
0
4. Valore della soluzione (nel problema di massimizzazione!):
Il vettore dato è esterno alla formulazione “cover”
-1/3-1/6=-1/2>-1
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 3
5. Arrotondamento della soluzione:
u3
u5
u2
u1
u4
u°3
u°5
u°2
u°1
u°4
1
1/2
0
0
0
1
1
0
0
0
Arrotondamento
6. Valore della soluzione associata ad u°: (nel problema di massimizzazione!):
-1/3-1/3=-2/3>-1
7. Il “cover” violato è:
u° è il vettore di incidenza di
un “cover” violato
x3+x5 < 1
Valutazione Esercizio 3:
-2 punti: se non viene calcolato l’ordinamento
-2 punti: per errori nell’applicazione dell’oracolo
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 4
4. ( punti 4 ) Descrivere la formulazione ottima e l’oracolo di separazione per il problema del minimo grafo
connesso s-t.
xe > 1
PS = {e
Risposta:
K taglio s-t
xe > 0e E
ORACOLO DI SEPARAZIONE
x^Rn
• Assegna peso ce=x^e a ciascun arco e E
• Calcola il taglio s-t di peso minimo K*
• Se c > 1
x^ > x^ > 1
x^ PS
• Se ce < 1
x^PS
e*
e*
e
e
e
e*
x^e <1
e*
e
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 5
5. (punti 4) Applicare l’oracolo descritto sopra e individuare una
disequazione (appartenente alla formulazione ottima) violata dalla
soluzione frazionaria mostrata a fianco (accanto ad ogni arco è indicato il
valore della corrispondente componente della soluzione frazionaria)
1
s
0
1
0
0
1 2/3
0
1
1/3 1/3
0
1/3
0
1/3
t
Soluzione: Bisogna trovare il taglio di capacità minima nel
grafo dato. Le capacità sono le componenti della soluzione
frazionaria
C
B
0
1
1
0
0
La disequazione violata è:
2/3
xCG+xDG+xFG+xFt > 1
1/3
1/3
0
A
0
1/3
1/3
E
Valutazione: punteggio massimo solo a
chi ha verificato la minimalità del taglio
(applicando Ford e Fulkerson o mostrando
un flusso di valore 1/3)
1
D 0
1
Il taglio ({s,A,B,C,D,E,F} ,{G,t}) è il taglio minimo (1/3) s
G
F
t
Modelli e Algoritmi della Logistica
Prova Scritta del 15/12/2003 B
SOLUZIONE ESERCIZIO 6
6. ( punti 3 ) Derivare la formula dell’EOQ e Calcolare l’EOQ per un problema di scorte con i seguenti
parametri: Domanda annuale 30; Costo unitario del bene 600; MARR= 4% ; Costo fisso = 40
1. La derivazione è quella descritta nelle pagine 6 e 7 della Lezione 17
2. L’EOQ desiderata è:
2 AD
Q 
r0v
*
=
24030
 0.04600
=
2400

24
=
Valutazione Esercizio 6:
-1 punto: se non viene dimostrata la formula in modo chiaro ed esplicativo
10