Il lavoro
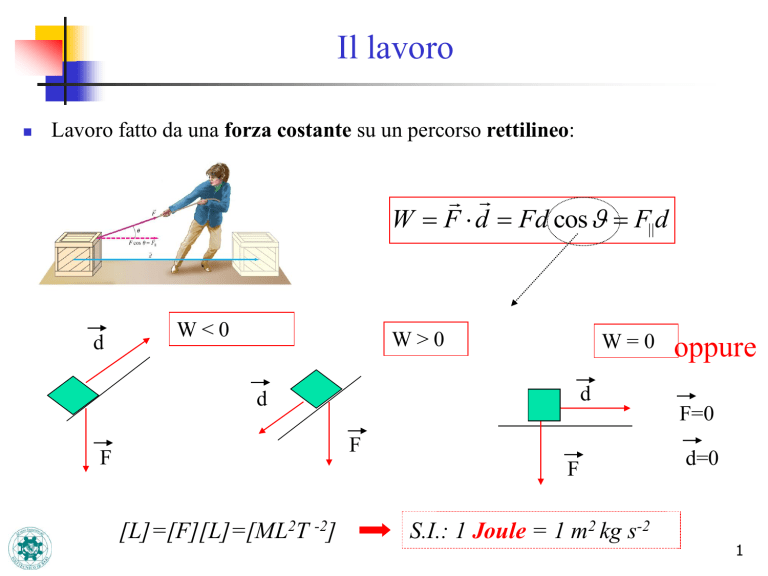
Lavoro fatto da una forza costante su un percorso rettilineo:
W F d Fd cos F||d
d
W<0
W>0
W=0
d
d
F=0
F
F
F
[L]=[F][L]=[ML2T -2]
oppure
S.I.: 1 Joule = 1 m2 kg s-2
d=0
1
Il lavoro
W F d Fd cos F||d
W F d Fx d x Fy d y Fz d z
È una grandezza scalare
Indipendente dalla scelta degli assi coordinati
2
Applicazione: Lavoro
Una persona traina una cassa di 50kg per 40 m lungo un pavimento orizzontale applicando una forza
costante Fp=100N e agente con un angolo di 37o. Il pavimento è scabro ed esercita una Fatt=50N.
Determinare il lavoro compiuto da ciascuna forza e il lavoro totale.
d 40mi
W F d Fx d x Fy d y Fz d z
Fp Fp cos i Fp sen j 79.8 N i 60.2 Nj
Fatt 50 Ni
P mgj 490 Nj
FN mg 490 Nj
WFp Fpx d x 3192 J
Watt Fattxd x 2000 J
WP P d 0
WFN FN d 0
Wtot W p Watt 1192 J
3
Potenza e lavoro
Data un forza che esegue un lavoro W in un intervallo di tempo Dt
si definisce potenza media nell’intervallo Dt il rapporto :
W
Pmedia
Dt
La Potenza sviluppata dalla forza all’istante t (potenza istantanea), si ottiene
facendo il limite per Dt che tende a zero:
P
dW
dt
Le dimensioni
[P] = [ML2T-2][T-1] = [ML2T-3]
Nel SI si misura in watt (W)
Unità di misura del lavoro la Kilowattora:
1kwattora=3.6MJ
dW F dr
dr
P
F
Fv
dt
dt
dt
4
Il Lavoro
Se la forza non è costante e/o il percorso non è rettilineo, possiamo:
dividere il percorso in tratti infinitesimi in modo da poter considerare
il tratto rettilineo e la forza costante su quel tratto
dW F ds
Calcolare il lavoro su ciascuno dei tratti
Sommare tutti i lavori calcolati sui singoli tratti
W F ds
F
f
ig
i
g
f
ds
5
Il Lavoro
Nel caso di più forze:
f
W
ig
f
f f
F1 F2 F3 ds F1 ds F2 ds F3 ds
ig
ig
ig
Il lavoro è pari alla somma dei lavori delle singole forze agenti,
ciascuno dei quali può essere: positiva, negativo oppure nullo
6
Il lavoro della forza elastica
A
B
Posizione di riposo
F p Forza esterna applicata
F M si oppone alla forza applicata (f. di richiamo)
in verso tale da riportare la molla nella posizione
di riposo
La forza elastica:
1. non constante
FM kxi
2. K costante elastica (N/m)
7
Il lavoro della forza elastica
A
B
WAB
B
A
WAB k
B
A
FM dr
1
xdx k x 2 B x 2 A 0
2
8
Teorema dell’energia cinetica
Consideriamo un punto materiale sul quale agisca:
R Fi costante
i
II legge di Netwon:
varia la sua velocità v e v
R ma s
i
f
Moto uniformemente accelerato
a
v f vi
Dt
1
s (vi v f )Dt
2
v f vi 1
1 2
1 2
W R s ma s m
(vi v f )Dt mv f mv i
Dt
2
2
2
9
Teorema dell’energia cinetica
Si definisce Energia cinetica della particella avente massa m e
velocità v:
1
E k mv 2
2
Teorema delle forze vive: la variazione dell’energia cinetica
subita dal punto materiale quando subisce uno spostamento
risulta uguale al lavoro compiuto dalla forza lungo il percorso.
W DEk
[Ek]=[M][v2]
S.I.: 1 m2 kg s-2 = 1
Joule
10
Teorema dell’energia cinetica
F
Generalizziamo il Teorema al caso di un
F non costante // asse x:
A
dr
B
dv x
dv x dx
dv x
F max m
m
m
vx
dt
dx dt
dx
W Fdx
W Fdx
v fx
v ix
dv x
m
v x dx
dx
1
2
2
mv x dv x m(v fx - v ix )
2
11
Energia-Lavoro: riassumiamo
l’energia cinetica è una grandezza che caratterizza il punto materiale:
dipende dallo stato di moto del corpo ma vedremo che esistono altre forme
di energia.
I corpi possono scambiarsi energia: il lavoro rappresenta un modo attraverso cui i
corpi si scambiano energia.
Se la risultante delle forze esterne compie un lavoro positivo (forza motrice,
concorde con il moto), allora l’energia cinetica del punto materiale aumenta.
Si dice che l’ambiente esterno ha compiuto un lavoro sul punto materiale
il punto materiale ha acquisito energia cinetica dall’ambiente esterno.
Se la risultante delle forze esterne compie un lavoro negativo (forza resistente,
opposta al moto), allora la sua energia cinetica diminuisce.
si dice che il punto materiale ha effettuato del lavoro sull’ambiente esterno
a spese della sua energia cinetica
W DEk
L’energia cinetica rappresenta la capacità di un corpo a compiere del lavoro cioè di
trasferire movimento ad altri corpi. La corrente del fiume fa muovere le macine di
un mulino!!
12
Urti elastici o anelastici
Dal punto di vista energetico gli urti si classificano
Elastici: si conserva l’energia cinetica
Anelastici: non si conserva l’energia cinetica:
Può sia diminuire (viene trasformata in altre forme di energia:
energia interna dei corpi, riscaldamento dei corpi)
Oppure può aumentare (l’energia interna dei corpi viene
trasformata in energia meccanica: esplosioni)
Urti completamente anelastici: quando i due corpi restano
attaccati dopo l’urto.
13
Urto completamente anelastico
14
Urto elastico
15
Lavoro nel moto rotatorio
Lavoro compiuto da una forza F su un corpo rigido che ruota attorno
ad un asse fisso:
F
r
dq
dL F ds Fsenfds Fsenfrdq
f
dL componente del momento
torcente di F attorno a z
dL z dq
qf
L z dq z (q f q i )
qi
16
Energia cinetica nel moto rotatorio
Corpo rigido che ruota attorno asse fisso
v1
vi ri
v2
1
1
2
K m i v i m i r 2 i 2
i 2
i 2
1 2
K I
2
1
K mv 2
2
17
Moto rototraslatorio
Combiniamo il moto rotatorio attorno asse passante per CM e
traslatorio nel piano xy
rn
P
CM
rCM
1
Mv 2 CM
2
1
2
K mi vi
i 2
ri rCM ri
v i v CM v i
1
1
m
(
v
v
)
m
(
v
v
)
(
v
v
i 2 i i i i 2 i CM i CM i )
1
2
mi (v CM 2vi v CM v 2 i )
i 2
1
1
2
K Mv CM I CM 2
2
2
v CM mi vi 0
vi ri
i
18












