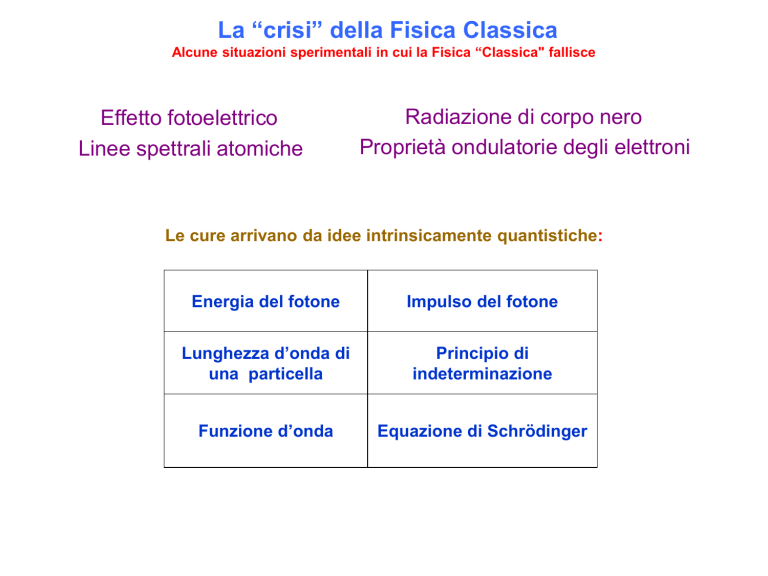
La “crisi” della Fisica Classica
Alcune situazioni sperimentali in cui la Fisica “Classica" fallisce
Effetto fotoelettrico
Linee spettrali atomiche
Radiazione di corpo nero
Proprietà ondulatorie degli elettroni
Le cure arrivano da idee intrinsicamente quantistiche:
Energia del fotone
Impulso del fotone
Lunghezza d’onda di
una particella
Principio di
indeterminazione
Funzione d’onda
Equazione di Schrödinger
La radiazione di Corpo Nero
La “Radiazione di Corpo Nero” o di "cavità” si riferisce ad un oggetto che assorbe tutta la
radiazione incidente su di esso e ri-irraggia energia che è caratteristica del suo solo sistema
irraggiante, e non dipende dal tipo di radiazione incidente. L’energia irradiata può essere
considerata come prodotta da onde stazionarie, o modi risonanti, della cavità che irraggia.
modi di radiazione
La quantità di radiazione emessa
in una certa banda di frequenze
dovrebbe essere proporzionale al
numero di modi in quella banda.
Secondo la Fisica Classica tutti i
modi hanno la stessa probabilità
di essere prodotti, ed il numero di
modi possibili nella cavità cresce
con il quadrato della frequenza.
Tuttavia, la continua crescita
di energia emessa con la
frequenza (denominata
"ultraviolet catastrophe") non
avviene. La Natura è più
saggia.
La nascita della Meccanica Quantistica
L’espressione quantistica della energia media per modo si ottiene partendo dalla
ipotesi di Planck: tutta la radiazione elettromagnetica è quantizzata e l’emissione
avviene per “quanti di energia”, che chiamiamo fotoni. Il quanto di energia di un
fotone è dato dal prodotto della costante di Planck h per la frequenza.
Questa quantizzazione implica che un fotone di luce, di data frequenza e
lunghezza d’onda, ha una energia quantistica fissata. Per esempio, un fotone di
luce blu, che ha una lunghezza d’onda di 450 nm, avrà sempre una energia di
2.76 eV. Tutta la luce blu è formata da fotoni di questa energia, e trasporta
energia in multipli di 2.76 eV. Non si può avere un mezzo fotone blu.
Energia massima e minima, Meccanica Quantistica e
Meccanica Classica
La frequenza disponibile è continua, senza limiti superiori o inferiori; quindi non
vi alcuna restrizione circa la possibile energia di un fotone. Per quanto riguarda
le energie alte, un limite pratico è semplicemente dovuto alla difficoltà di
trovare meccanismi per la creazione di fotoni ad altissima energia. I fotoni di
bassa energia invece abbondano; tuttavia, quando si scende sotto il limite
delle frequenze radio, le energie dei fotoni sono così piccole, confrontate con
le energie termiche a temperatura ambiente, che non si potranno mai isolare
come singole entità quantizzate. Si perdono semplicemente nella energia di
fondo presente. In altre parole, nel limite di basse frequenze la trattazione della
radiazione elettromagnetica si fonde con la descrizione classica ed una
trattazione quantistica non è più necessaria.
Densità di energia del Corpo Nero in funzione della frequenza
Energia per
unità di volume
e di frequenza
k = costante di
Boltzman
Rayleigh-Jeans vs Planck
Confronto tra la legge classica di Rayleigh-Jeans e la formula della radiazione
quantistica di Planck. L’ esperimento conferma la relazione di Planck.
Curve di Radiazione
L’effetto fotoelettrico
Gli aspetti incomprensibili
dell’effetto fotoelettrico quando si
incominciò ad osservarlo erano:
1. Gli elettroni venivano emessi
immediatamente - nessun ritardo!
2. Un aumento della intensità
della luce causava un aumento
del numero di fotoelettroni, ma
non della loro energia cinetica!
Le caratteristiche dell’effetto fotoelttrico
erano in netta contraddizione con le
predizioni della Fisica Classica. La
spiegazione dell’effetto segnò uno dei
passi fondamentali verso la Teoria dei
Quanti.
3. La luce rossa non provoca
emissione di elettroni, qualunque
sia la sua intensità!
4. Una debola luce violetta causa
l’emissione di pochi elettroni, ma la
loro energia cinetica è maggiore di
quella ottenuta con luce più intensa
di frequenza minore!
L’effetto fotoelettrico
L’analisi dei dati dell’effetto fotoelettrico mostrò
che l’energia degli elettroni emessi era
proporzionale alla frequenza della luce incidente.
Ciò mostrava che qualunque “cosa” estraesse gli
elettroni dal metallo aveva un’energia
proporzionale alla frequenza della luce. Il fatto
sorprendente che l’energia dei singoli elettroni
fosse indipendente dalla energia totale della luce
incidente (cioè l’intensità), mostrava che
l’interazione della luce con il metallo deve essere
come quella di una singola particella che cede la
sua energia all’elettrone. Ciò è consistente con
l’ipotesi di Planck, da lui applicata al problema
della radiazione del Corpo Nero, secondo cui la
luce è formata da quanti discreti (fotoni), ciascuno
con energia:
E hν
I fenomeni luminosi più comuni possono essere spiegati e descritti mediante
la natura ondulatoria della luce. Invece, l’effetto fotoelettrico suggerisce una
natura corpuscolare della luce.
Il problema degli spettri atomici
Negli anni alla fine del 1900, si osservò che la luce
emessa da gas luminosi non mostrava una distribuzione
continua di lunghezze d’onda, ma formava un insieme
discreto di colori, diversi per i vari gas. Queste "linee
spettrali" si disponevano in una serie regolare e si
giungerà ad interpretarle come transizioni tra livelli atomici
di energia. Allora, rappresentavano un grosso problema
per la Fisica Classica. Si sapeva che particelle cariche
accelerate emettono onde elettromagnetiche, e ci si
aspettava che orbite di elettroni intorno ai nuclei fossero
instabili, in quanto, a causa della perdita di energia
elettromagnetica emessa, sarebbero stati attratti dal
nucleo. Non si poteva trovare alcun modello classico che
portasse ad orbite stabili degli elettroni.
Il modello atomico di Bohr segnò il passo fondamentale
verso una moderna teoria atomica. Il punto fondamentale
fu il postulato che il momento angolare è quantizzato,
permettendo di ottenere solo specifici livelli di energia. In
seguito, lo sviluppo della Meccanica Quantistica e
l’equazione di Schrödinger permisero di comprendere i
postulati ed I risultati del modello all’interno di una teoria
completa e consistente.
Helium spectrum
Hydrogen spectrum
1
1 n , n interi
RH 2 2 1 2
n1 n2 (n1 n2 )
1
RH, costante di Rydberg
= 1.097 10–7 m–1
Il modello atomico di Boh – Orbita classica dell’elettrone
Nel modello di Bohr, questo risultato classico fu combinato con la quantizzazione del
momento angolare, per ottenere un’espressione dei livelli quantizzati di energia.
La quantizzazione del momento angolare
Nel modello di Bohr la lunghezza d’onda associata all’elettrone è data dalla relazione di
de Broglie (si vedano le trasparenze successive)
h
h
p mv
a cui si unisce la condizione di stazionarietà: lunghezza della circonferenza = numero
intero di lunghezze d’onda
2 r n
Queste due condizioni si combinano per dare l’espressione quantizzata del momento
angolare per l’elettrone in orbita:
L mvr
hr
hr
nh
n
2 r n 2
Quindi L non solo è conservato (non dipende dal tempo), ma è costretto ad assumere
valori discreti, multipli di h/2π secondo il numero quantico n. Questa quantizzazione del
momento angolare è un risultato fondamentale e può essere usato per determinare I
raggi e le energie delle orbite di Bohr.
Combinando il procedimento seguito nel caso classico con la quantizzazione del
momento angolare, l’approccio di Bohr fornisce le espressioni per i raggi e le energie
delle orbite degli elettroni:
vale per atomi
idrogenoidi: Z protoni
e 1 elettrone
energia cinetica
dell’elettrone
espressa in
funzione del
momento
angolare
uso della
condizione di
quantizzazione
energia cinetica
orbitale classica
da queste espressioni si ricava:
13.6 eV 2
Z
2
n
a0 = 0.529 10–10 m = raggio di Bohr
n = 1,2,3,…
Livelli di energia dell’atomo di idrogeno
I livelli di energia dell’atomo di idrogeno sono in accordo con quelli del modello di Bohr.
La descrizione pittorica usuale è quella di una struttura ad orbite (o gusci), con ogni
orbita associata ad uno dei valori del numero quantico principale n.
La descrizione dell’atomo tramite le orbite del modello di Bohr è una utile visualizzazione;
non bisogna tuttavia dimenticare che, come risulterà dalla Meccanica Quantistica, i concetti
di orbita e raggio orbitale saranno sostituiti da concetti quali la distribuzione di probabilità di
posizione.
Il modello di Bohr prevede che gli elettroni occupino una delle possibili orbite
quantizzate, senza emissione di onde elettromagnetiche. L’emissione avviene quando
l’elettrone passa da un’orbita all’altra; in questa transizione avviene l’emissione di un
fotone di energia pari alla differenza di energia tra le due orbite.
h E2 E1
Dall’espressione dei livelli quantizzati di energia si ha
1
me4 1
1
1
h
2 13.6 2 2 eV
2 2 2
8 0 h n1 n2
n1 n2
Questa relazione può essere scritta come h
con
hc
me4
RH
2
8 0 ch3
RH 1.097 107 m1
Le debolezze del modello di Bohr
Anche se il modello di Bohr rappresentò un passo avanti fondamentale
verso la costruzione della teoria quantistica degli atomi, non rappresenta in
realtà la corretta descrizione teorica della natura delle orbite elettroniche.
Le sue principali manchevolezze sono:
1. Non permette di capire perché certe linee spettrali sono più luminose di
altre. Non vi è alcun meccanismo che permetta di calcolare la probabilità di
transizione tra livelli atomici.
2. Il modello di Bohr considera gli elettroni come pianeti in miniatura, in
rotazione intorno al nucleo con un ben preciso raggio ed impulso. Questo
viola il principio di indeterminazione, secondo cui posizione ed impulso non
possono essere esattamente determinati contemporaneamente.
Il modello di Bohr ci fornisce un modello concettualmente semplice e
fondamentale delle orbite e delle energie degli elettroni atomici. I dettagli
dello spettro e della distribuzione di cariche sono ottenibili solo dai calcoli
della Meccanica Quantistica e dell’equazione di Schrödinger. Molti dei
risultati del modello di Bohr (compresa la sua ipotesi di quantizzazione )
saranno ritrovati all’interno di una teoria completa e consistente.
La natura particellare della luce – Lo scattering Compton
Compton osservò la deflessione di
raggi X da parte di elettroni, trovando
che i raggi X deflessi avevano una
lunghezza d’onda più grande di quella
dei raggi incideni. La variazione della
lunghezza d’onda aumentava con
l’angolo di deflessione, secondo la
formula (di Compton):
Compton spiegò i dati assumendo una
natura particellare della luce (fotoni)
ed applicando la coservazione
dell’energia e dell’impulso alla
collisione tra un fotone e l’elettrone. Il
fotone deflesso ha un’energia minore e
quindi una maggiore lunghezza d’onda,
secondo la relazione di Planck.
L’espressione precedente per Δλ può essere ottenuta imponendo la conservazione
dell’energia e dell’impulso:
h i mec 2 h f pe2c 2 me2c 4
pi p f pe
conservazione dell’energia
conservazione dell’impulso
La natura ondulatoria dell’elettrone
Giovane studente a Parigi, Louis DeBroglie aveva appreso la relatività e l’effetto
fotoelettrico. Quest’ultimo evidenziava la natura corpuscolare della luce, da sempre
considerata un fenomeno ondulatorio. Egli si chiese se gli elettroni ed altre "particelle"
potessero a loro volta esibire proprietà ondulatorie. Questo condurrà ad una nuova teoria.
La conferma dell’ipotesi di DeBroglie arrivò grazie
all’esperimento di Davisson- Germer. Esso mostrò
figure di interferenza – in accordo con la lunghezza
d’onda di DeBroglie – per l’urto di elettroni su
cristalli di nickel.
Quando i raggi X sono deflessi dal reticolo cristallino,
si osservano picchi di intensità finale corrispondenti
alla condizione di Bragg, secondo cui si hanno
massimi quando la differenza di cammino di due raggi
è uguale ad un multiplo intero della lunghezza d’onda.
Tale formula può essere usata in più modi:
conoscendo d e misurando theta, si ricava lambda,
oppure conoscendo lambda si ricava d.
Simili figure di interferenza furono osservate con
elettroni. L’energia degli elettroni, e quindi la loro
lunghezza d’onda, può essere variata, variando il
potenziale di accelerazione.
L’esperimento di DavissonGermer dimostrò che anche gli
elettroni presentano fenomeni
ondulatori, in accordo con la
lunghezza d’onda di DeBroglie:
lunghezza d’onda di
un elettrone di
impulso p
La lunghezza d’onda di DeBroglie
La dualità Onda-Particella per la luce
La luce consiste di particelle o di onde? La risposta dipende dai tipi di fenomeni che si
osservano:
Fenomeno
Può essere spiegato in termini
di onde
Può essere spiegato in termini
di particelle
Refessione
Rifrazione
Interferenza
Diffrazione
Polarizzazione
Effetto fotoelettrico
Compton scattering
I più comuni fenomeni luminosi osservati possono essere spiegati come fenomeni ondulatori.
Tuttavia l’effetto fotoelettrico e lo scattering Compton suggerirono una natura particellare per la
luce. Lo stesso dualismo onda-particella fu osservato anche per gli elettroni.
( x, t )
La funzione
d’onda
Ogni particella è rappresentata da una funzione d’onda Ψ (x,t) tale che
Ψ* Ψ è la probabilità di trovare la particella nel punto x al tempo t.
La funzione d’onda è soluzione dell’equazione di Schrödinger. Questa
equazione gioca lo stesso ruolo della legge di Newton e della
conservazione dell’energia nella Meccanica Classica, cioè predice il
comportamento futuro di un sistema dinamico. Predice analiticamente
e precisamente le probabilità di eventi e risultati futuri. I dettagli dei
risultati dipendono dal caso, ma, per un grande numero di eventi,
l’equazione di Schrödinger, predirrà la loro distribuzione statistica.
Le proprietà della funzione d’onda
contiene tutte le informazioni fisiche (misurabili) sulla particella
se la particella esiste, la probabilità totale
*
dV
1
è continua (insieme alla sua derivata)
di trovarla è 1
permette il calcolo del valore medio (valore di aspettazione)
di qualunque grandezza fisica
Per una particella libera è un’onda piana; ciò implica un
preciso valore p dell’impulso e p2/2m dell’energia, ed una
totale incertezza nella posizione
L’equazione di Schrödinger
L’energia cinetica e potenziale sono trasformate nell’operatore Hamiltoniano, che agisce sulla
funzione d’onda per generarne l’evoluzione nello spazio e nel tempo. L’equazione di
Schrödinger dà l’energia quantizzata del sistema (i possibili valori di E) e la forma della
funzione d’onda, a partire dalla quale altre proprietà fisiche possono essere calcolate.
L’equazione di Schrödinger indipendente dal tempo
Per un potenziale generico U l’equazione di Schrödinger unidimensionale ed
indipendente dal tempo è
2 d 2 ( x)
U ( x) ( x) E ( x)
2
2m dx
In 3 dimensioni assume la forma
2
2m
2 2 2
2 2 2 U ( x, y, z )( x, y, z ) E ( x, y, z )
y
z
x
per coordinate cartesiane. Può essere scritta in modo più compatto, introducendo
l’operatore Laplaciano
2
2
2
f
f
f
2 f 2 2 2
x
y
z
L’equazione di Schrodinger può quindi essere scritta come:
2 2
U ( x, y, z ) ( x, y, z ) E ( x, y, z )
2m
Hˆ E
L’equazione di Schrödinger dipendente dal tempo
L’equazione di Schrödinger dipendente dal tempo, in una dimensione spaziale, ha la forma
2 2 ( x, t )
( x, t )
U ( x) ( x, t ) i
2
2m
x
t
Per una particella libera , per la quale U(x) =0, la funzione d’onda, soluzione dell’equazione,
può essere scritta come un’onda piana
i ( k x t )
( x, t ) Ae
k
2
2
p
h
2π
2
2
E
T
h
Per altri problemi, cioè per particelle soggette ad una forza, il potenziale non nullo rende la
soluzione più difficile. La dipendenza spaziale della funzione d’onda è fissata dall’equazione
di Schrödinger indipendente dal tempo mentre l’evoluzione temporale da quella dipendente
dal tempo
I postulati della Meccanica Quantistica
1. Il postulato della Funzione d’Onda:
Associata ad ogni particella che si muove in un campo di forze conservative vi
è una funzione d’onda, la quale determina tutte le informazioni ottenibili sul
sistema.
Ad ogni sistema fisico formato da una particella è associata una funzione d’onda. Questa
funzione d’onda permette di ottenere tutte le informazioni possibili sul sistema. La funzione
d’onda può anche essere complessa; è il prodotto con la funzione complessa coniugata
che specifica la vera probabilità fisica di trovare la particella in un certo stato.
( x, t )
ampiezza di probabilità, calcolata in x ,t
( x, t ) ( x, t )
*
probabilità di trovare la
particella in x ,t
Probabilità in Meccanica Quantistica
La funzione d’onda rappresenta l’ampiezza di probabilità di trovare la particella in un
certo punto dello spazio, ad un certo istante. La vera probabilità di trovare la particella
è data dal prodotto della funzione d’onda (che può essere un numero complesso) con il
suo complesso coniugato; il risultato è sempre un numero reale (l’analogo del
quadrato, per una funzione complessa).
( x, y, z, t ) ampiezza di probabilit à
* probabilit à
Poiché la probabilità totale di trovare la particella da qualche parte deve essere = 1, la
funzione d’onda deve essere normalizzata. Cioè la somma delle probabilità, estesa a
tutto lo spazio, deve essere 1. Ciò si esprime tramite l’integrale:
*
dV 1
dV dx dy dz Volume infinitesimo
La richiesta di avere funzioni d’onda normalizzabili svolge un ruolo molto importante
nella ricerca delle soluzioni dell’equazione di Schrödinger. Ad esempio, si può trovare
che solo certi valori dell’energia permettono di ottenere soluzioni normalizzabili.
2. Il postulato degli operatori associati a grandezze fisiche
Per ogni osservabile fisica q esiste un operatore associato Q, il quale, quando opera
su una funzione d’onda associata ad un valore definito di quella osservabile, dà
come risultato la stessa funzione d’onda moltiplicata per quel valore dell’osservabile.
Per ogni osservabile fisica si introduce un operatore matematico associato che
agisce sulla funzione d’onda, dando come risultato, in generale, un’altra funzione.
Supponiamo che la funzione d’onda Ψn (autofunzione) sia associata ad un particolare
valore qn (autovalore) della osservabile e che l’operatore sia indicato con Q. L’azione
dell’operatore è data da:
L’operatore matematico Q estrae il valore qn dell’osservabile, operando sulla funzione
d’onda che rappresenta quel particolare stato del sistema. Questo processo è collegato
alla teoria della misura in Meccanica Quantistica. Ogni funzione d’onda di un sistema
quantistico può essere rappresentata come una combinazione lineare delle autofunzioni
Ψn (si veda il postulato del sistema completo). Quindi l’operatore Q può essere usato per
estrarre una combinazione lineare di autovalori, ciascuno moltiplicato per un coefficiente;
questo è legato alla probabilità di ottenere come risultato della misura proprio l’autovalore
corrispondente (si veda il postulato del valore di aspettazione).
Operatori in Meccanica Quantistica
Associato ad ogni grandezza misurabile di un sistema fisico vi è un operatore quantistico.
In Meccanica Quantistica si descrivono i sistemi fisici mediante onde (la funzione d’onda),
piuttosto che tramite particelle il cui moto e la cui dinamica possono essere descritti con
precisione dalle equazioni deterministiche della Fisica di Newton. Questi operatori
possono essere rappresentati in vari modi. Alcuni sono elencati qui di sotto:.
In questa rappresentazione (detta di Schrödinger) degli operatori, le posizioni e le loro
funzioni non cambiano, mente gli impulsi diventano derivate rispetto alla posizione.
L’operatore dell’energia (Hamiltoniano) contiene derivate rispetto allo spazio ed al tempo.
3. Il postulato e le proprietà dell’operatore Hermitiano
Ogni operatore Q associato ad una grandezza fisica osservabile è Hermitiano
Ogni operatore quantistico Q, associato ad una grandezza fisica reale e misurabile, deve
essere Hermitiano, cioè soddisfare la seguente proprietà:
*
*
(
Q
)
dV
(
Q
)
a b
a b dV
dove Ψa e Ψb sono funzioni arbitrarie normalizzabili, e l’integrazione è su tutto lo spazio.
La richiesta è fisicamente necessaria, in quanto assicura che i valori misurati (cioè gli
autovalori) siano numeri reali.
Teorema: se Q è Hermitiano,
allora tutti i qi sono numeri
reali
Inoltre, se Q è hermitiano,
per ogni i ≠ j si ha:
*
i j dV 0
4. Il teorema dell’insieme completo
L’insieme delle autofunzioni di un operatore Hermitiano Q forma un insieme
completo (una base) di funzioni linearmente indipendenti
L’insieme delle funzioni Ψj, che sono autofunzioni dell’equazione agli autovalori
forma un insieme completo di funzioni linearmente indipendenti. Esse formano una base:
vale a dire che qualunque funzione d’onda che rappresenti il sistema può essere scritta
come combinazione lineare delle funzioni della base:
Ciò implica che qualunque funzione d’onda Ψ che descrive il sistema fisico può essere
scritta come combinazione lineare delle autofunzioni di qualunque osservabile fisica del
sistema.
5. Il postulato del valore di aspettazione
Per un sistema descritto da una data funzione d’onda Ψ, si può calcolare il valore di
aspettazione di qualunque grandezza fisica q, alla quale è associato l’operatore Q.
Per un sistema fisico descritto da una funzione d’onda Ψ, il valore di aspettazione di
una qualunque osservabile fisica q può essere espresso in termini del corrispondente
operatore hermitiano Q e della funzione d’onda, nel modo seguente:
q *Q dV
La funzione d’onda deve essere normalizzata e l’integrale è esteso a tutto lo spazio.
Questo postulato diviene intuitivo se si considera il postulato dell’operatore
Hermitiano e il teorema dell’insieme completo. La funzione d’onda può essere
rappresentata come una combinazione lineare delle autofunzioni di Q, ed il risultato
dell’integrale dà la somma di tutti i possibili valori fisici (gli autovalori di Q), ciascuno
moltiplicato per un coefficiente (una probabilità). L’integrale dà quindi la media pesata
di tutti i possibili valori dell’osservabile.
Un sistema fisico è descritto dalla funzione d’onda Ψ, la quale può sempre
essere scritta come una combinazione lineare delle autofunzioni dell’operatore
Hermitiano Q:
cn n
Q n qn n
n
Se uno inserisce questa espressione nell’integrale del valore di aspettazione, trova
q | cn | qn
2
n
con la seguente interpretazione: una misura di Q per lo stato Ψ darà come
risultato uno qualunque dei suoi autovalori qn, ciascuno con una probabilità |cn|2.
La condizione di normalizzazione della funzione d’onda implica:
2
|
c
|
n 1
n
Una misura di Q forza il sistema a diventare uno dei possibili autostati
(autofunzioni) di Q, Ψn: ogni eventuale misura successiva di Q darà sempre
come risultato qn
6. L’ evoluzione temporale
L’evoluzione temporale della funzione d’onda è data dalla equazione di
Schrödinger dipendente dal tempo.
Se Ψ(x,y,z; t) è la funzione d’onda di un sistema fisico ad un tempo t ed il sistema
è libero da interazioni esterne al sistema, allora l’evoluzione nel tempo della
funzione d’onda è data
dove H è l’operatore Hamiltoniano formato a partire dall’espressione dell’Hamiltoniana
classica e sostituendo le osservabili classiche con i corrispondenti operatori quantistici.
Il ruolo dell’Hamiltoniano nella dipendenza spaziale e temporale della funzione d’onda è
espresso dalle equazioni di Schrödinger.
1. Associata ad ogni particella che si muove in un campo di forze
conservative esiste una funzione d’onda, la quale contiene tutte le
informazioni che si possono ottenere sul sistema.
2. Ad ogni osservabile fisica q corrisponde un operatore associato Q, il
quale, quando opera sulla funzione d’onda associata ad un particolare
valore di quella osservabile, dà come risultato la stessa funzione d’onda
moltiplicata per quel valore dell’osservabile.
3. Ogni operatore Q associato ad una proprietà fisica misurabile, è un
operatore Hermitiano
4. L’insieme di autofunzioni di ogni operatore Hermitiano Q forma un
insieme completo (o base) di funzioni linearmente independenti.
5. Per un sistema fisico descritto da una data funzione d’onda, il
valore di aspettazione (o valor medio) di qualunque grandezza fisica
q si trova calcolando l’integrale del valore di aspettazione rispetto a
quella funzione d’onda.
6. L’evoluzione temporale della funzione d’onda è dato dalla equazione
di Schrödinger dipendente dal tempo.
Una particella libera e l’equazione di Schrödinger
L’equazione di Schrödinger non può essere dedotta; la sua validità viene dal
confronto con i dati sperimentali. La naura ondulatoria di un elettrone è chiaramente
confermata da esperimenti come quello di Davisson-Germer. Ciò fa sorgere la
domanda: “Cosa è questa natura ondulatoria?". La risposta, a posteriori, è che
questa natura ondulatoria si manifesta attraverso la funzione d’onda dell’elettrone. La
soluzione dell’equazione di Schrödinger per una particella libera è un’onda piana, la
quale contiene la relazione di deBroglie per l’impulso e di Planck per l’energia.
h
2
E’ più facile mostrare la relazione con l’equazione di Schrödinger scrivendo l’onda piana
in forma esponenziale usando la relazione di Eulero. Questa è l’espressione usuale per la
funzione d’onda di una particella libera.
(ei cos i sin )
Si può verificare che Ψ è autofunzione degli operatori impulso ed energia
Il collegamento con l’equazione di Schrödinger si può fare esaminando l’espressione
per l’energia per particelle e per onde (fotoni)
Assumendo l’equivalenza di queste due espressioni and inserendo I loro corrispondenti
operatori quantistici, ci porta all’equazione di Shrödinger
Il principio di indeterminazione
La posizione e l’impulso di una particella non possono essere misurati
simultaneamente con precisione arbitraria. Il prodotto delle incertezze delle
due misure ha un minimo. Lo stesso principio vale per la misura
contemporanea di energia e tempo.
Questo principio non riguarda il limite proprio degli strumenti di misura, o
limiti derivanti dalla accuratezza dei metodi sperimentali. Deriva dalle
proprietà ondulatorie intrinseche alla descrizione quantistica della natura.
Anche con strumenti e tecniche perfetti, questa incertezza rimane, intrinseca
alla natura delle cose.
Il principio di indeterminazione
La dualità onda-particella e la relazione di DeBroglie aiutano a comprendere tale
principio. Man mano che si scende verso dimensioni atomiche, non è più valido
considerare una particella come una sfera rigida, perché più piccole sono le dimensioni e
più “ondosa” essa diviene. Non ha più senso dire che si conoscono precisamente la
posizione e l’impulso di tale particella.
La definizione esatta di Δx e Δp è
x x 2 x 2
p p 2 p 2
x p
2
Il confinamento di particelle
Calcolo della energia di confinamento
L’atomo di idrogeno
La soluzione dell’equazione di
Schrödinger per l’atomo di
idrogeno si ottiene più facilmente
usando coordinate polari sferiche e
separando le variabili, così che la
funzione d’onda è rappresentata
dal prodotto:
La separazione conduce a tre
equazioni separate per le tre variabili
spaziali, e le loro soluzioni portano ai
tre numeri quantici associati con i
livelli di energia dell’atomo di idrogeno.
I numeri quantici per l’atomo di idrogeno
La soluzione dell’equazione di Schrödinger per l’atomo di idrogeno richiede di imporre la
condizione che le funzioni d’onda siano normalizzabili. Queste soluzioni, per le tre funzioni
separate delle tre variabili, possono esistere soltanto se certe costanti che appaiono nelle
equazioni assumono valori interi. Ciò porta ai numeri quantici dell’atomo di idrogeno:
H nlm En nlm
En
13.6
eV
2
n
n = principal quantum number
L2 nlm l (l 1) 2 nlm
l = orbital quantum number
Lz nlm ml nlm
ml = magnetic quantum number
Il modello vettoriale per il momento angolare orbitale
Il momento angolare orbitale per un elettrone atomico
può essere visualizzato mediante un modello
vettoriale, nel quale il vettore momento angolare
effettua un moto di precessione intorno ad una
direzione fissa nello spazio. Mentre la lunghezza del
vettore ha il valore indicato, solamente un massimo di
l unità of ħ può essere misurato lungo una certa
direzione, dove l è il numero quantico orbitale.
Anche se lo si definisce "vettore", il momento
angolare orbitale in Meccanica Quantistica è un
tipo speciale di vettore; infatti la sua proiezione
lungo una direzione nello spazio è quantizzata, con
valori che differiscono di una unità ħ. Il diagramma
mostra che i possibili valori del “numero quantico
magnetico" ml (for l =2), sono
ml 2, 1, 0, 1, 2
Lo spin dell’elettrone
Lo spin di un elettrone, s = 1/2, è una proprietà
intrinseca degli elettroni. In aggiunta al momento
angolare orbitale gli elettroni posseggono un momento
angolare intrinseco, caratterizzato dal numero quantico
1/2. In analogia al momento angolare orbitale, si ha:
11
S 2 spin 1 2 spin
22
1
S z spin ms spin spin
2
ms= ½ “spin su”
ms= – ½ “spin giù”
I due stati di spin, “su" e “giù“, permettono di avere due elettroni per ogni insieme degli
altri numeri quantici n, l , ml
nlml ms
Il Principio di Esclusione di Pauli
Due elettroni in un atomo non possono avere gli stessi numeri quantici.
Questo è un esempio di un principio generale che si applica non solo agli elettroni,
ma anche a tutte le altre particelle di spin semi-intero (fermioni). Non si applica alle
particelle di spin intero (bosoni).
La natura del principio di esclusione di Pauli può essere illustrata supponendo che
gli elettroni 1 e 2 siano negli stati a e b rispettivamente. La funzione d’onda per il
sistema dei due elettroni sarebbe
Ma questa funzione d’onda è inaccettabile
perché gli elettroni sono identici e non
distinguibili. Ogni stato può essere occupato
da uno qualunque dei due elettroni, e, per
tener conto di ciò, dobbiamo usare una
combinazione lineare delle due possibilità..
La funzione d’onda per il sistema in cui entrambi gli stati "a" e "b" sono
occupati dagli elettroni può essere scritta come:
Il principio di esclusione di Pauli è parte di una delle nostre più fondamentali osservazioni
della natura: particelle identiche di spin semi-intero debbono avere una funzione d’onda
antisimmetrica, mentre particelle identiche di spin intero debbono avere una funzione
d’onda simmetrica. Il segno meno relativo tra i due termini costringe la funzione d’onda
dei fermioni ad annullarsi identicamente se i due stati "a" e "b“ sono identici; ciò implica
che è impossibile che entrambi gli elettroni occupino lo stesso stato.
Applicazioni del principio di esclusione di Pauli
La Tabella Periodica degli Elementi
I numeri quantici associati agli elettroni atomici, insieme al principio di esclusione di
Pauli, forniscono le proprietà fondamentali per la costruzione delle strutture atomiche e
la comprensione della Tabella Periodica degli Elementi.
Per un dato numero quantico principale n, vi sono 2n2 diversi stati possibili
(con la stessa energia).
L’ordine di occupazione dei livelli di energia atomici da parte degli elettroni avviene a
partire da quelli di energia pù bassa, e prosegue consistentemente con il principio di
Pauli. L’indicazione dei livelli segue lo schema della notazione spettroscopica.
La notazione spettroscopica
Prima che la natura degli stati atomici degli elettroni fosse chiarificata dalla Meccanica
Quantistica, lo studio degli spettri di radiazione emessi dagli atomi (spettroscopia) fece
osservare l’esistenza di serie tipiche, alle quali furono assegnate lettere. In funzione dei
numeri quantici degli stati elettronici, la notazione è la seguente:
L’ordine di riempimento degli stati elettronici
Man mano che la tabella periodica degli elementi è
costruita, aggiungendo elettroni fino a raggiungere il numero
atomico, sono occupati gli stati di energia più bassa,
permessi dal principio di esclusione di Pauli. La massima
occupazione di ciascun livello è determinata dai numeri
quantici, ed il diagramma a sinistra illustra l’ordine di
riempimento dei livelli energetici.
Per un singolo elettrone l’energia è determinata dal numero
quantico principale n, e quel numero quantico è usato per
indicare la "shell (guscio)" in cui si sistemano gli elettroni.
Per una data shell in atomi multi-elettronici, gli elettroni con
un numero quantico orbitale l inferiore avranno energia più
bassa, se si tiene conto della loro energia di interazione con
gli altri elettroni. Questi livelli di energia sono specificati dai
numeri quantici principali ed orbitali, usando le notazioni
spettroscopiche. Quando si raggiunge il livello 4s, la
dipendenza dal numero quantico orbitale è così forte che
l’energia del livello 4s è inferiore a quella del livello 3d. A
parte qualche piccola eccezione, l’ordine di riempimento
segue lo schema indicato nel diagramma, con la freccia che
indica i punti nei quali si procede verso shell successiva,
piuttosto che verso il livello con un maggiore numero
quantico orbitale nella stessa shell.
La divisione in “gusci” (shells) può suggerire l’idea di un "modello planetario" per gli
elettroni; anche se non è del tutto accurata, questa descrizione ha un valore mnemonico
ed intuitivo per aiutare a comprendere la struttura degli elementi più pesanti.
La configurazione orbitale degli elettroni fornisce una schema utile per capire le
reazioni chimiche, che sono guidate dal principio di trovare le configurazioni degli
elettroni con energia più bassa (le più stabili). Si dice che il sodio ha una valenza di
+1 poiché tende a perdere un elettrone, e il cloro ha una valenza di -1 poiché ha la
tendenza ad acquistare un elettrone. Entrambi questi atomi sono molto attivi
chimicamente, e la loro combinazione (cloruro di sodio) è il classico caso di un
legame ionico.
La condensazione di Bose-Einstein
Nel1924 Einstein notò che i bosoni possono "condensare" in numero illimitato
in un singolo stato fondamentale, in quanto obbediscono alla statistica di
Bose-Einstein e non hanno le restrizioni derivanti dal principio di esclusione
di Pauli. Ciò fu poco notato, fino a quando il comportamento anomalo dell’elio
liquido a basse temperature fu studiato attentamente.
Quando l’elio è raffreddato alla temperatura critica di 2.17 K, avviene una
impressionante cambio nel valore della capacità termica, la densità del liquido
precipita e una parte di esso diventa "superfluido”, a zero viscosità. La
superfluidità è originata dalla frazione di atomi di elio che sono condensati alla
più bassa energia possibile.
Un effetto di condensazione è anche ritenuto responsabile per il fenomeno
della superconduttività. Nella teoria BCS, coppie di elettroni si uniscono per
formare le cosiddette coppie di Cooper, le quali si comportano come bosoni e
possono condensare in uno stato di resistenza elettrica nulla.












