trasparenze ppt

Manubrio simmetrico
•
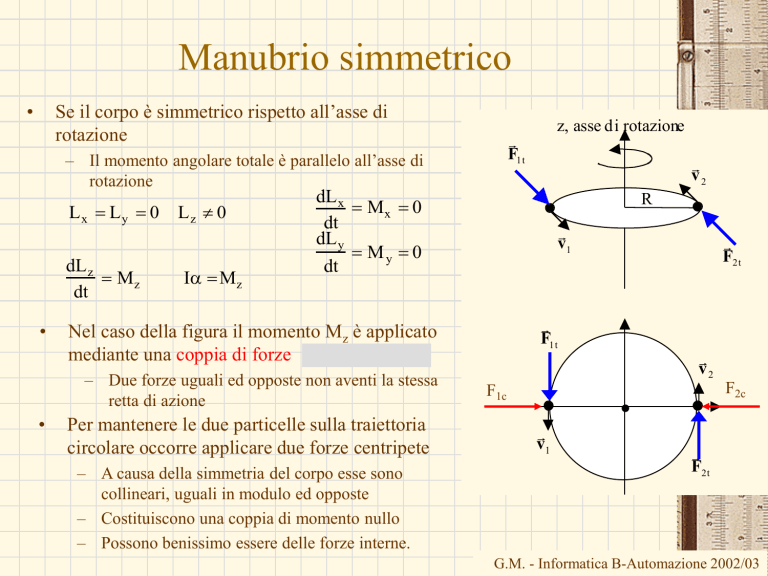
Se il corpo è simmetrico rispetto all’asse di
rotazione
z, asse di rotazione
F1t
– Il momento angolare totale è parallelo all’asse di
rotazione
Lx  Ly  0
dL z
 Mz
dt
•
Lz  0
I  Mz
dL x
 Mx  0
dt
dL y
 My  0
dt
R
v1
Nel caso della figura il momento Mz è applicato
mediante una coppia di forze
– Due forze uguali ed opposte non aventi la stessa
retta di azione
•
v2
Per mantenere le due particelle sulla traiettoria
circolare occorre applicare due forze centripete
– A causa della simmetria del corpo esse sono
collineari, uguali in modulo ed opposte
– Costituiscono una coppia di momento nullo
– Possono benissimo essere delle forze interne.
F2t
F1t
v2
F1c
v1
z,
 di
asse
rotazione
F2c
F2t
G.M. - Informatica B-Automazione 2002/03
Coppia di forze
•
•
•
•
Due forze uguali ed opposte non aventi la stessa retta di
azione
Attraverso una coppia è possibile applicare al corpo un
momento puro
La risultante della coppia è nulla.
Il momento della coppia invece è indipendente dal polo
O
F
b
F
   

r
– Per esempio rispetto ad O, il punto di applicazione della
forza F:
M1=0, M2=rFsen rFsen(-=Frsen(-=Fb
•
•
•
•
È diretto perpendicolarmente al piano della coppia
Nel caso considerato il verso è uscente
Il modulo vale Fb dove b è il braccio della coppia pari alla
distanza tra le retta di azione delle due forze
Se le due forze sono collineari il momento della coppia è
nullo
F
F
b
• Lo stesso momento può essere ottenuto in infiniti modi diversi.
G.M. - Informatica B-Automazione 2002/03
Manubrio asimmetrico
•
Se il corpo non è simmetrico rispetto all’asse di
rotazione, e l’asse di rotazione non è un asse
principale d’inerzia
z, asse di rotazione
– Il momento angolare totale non è parallelo all’asse
di rotazione
•
Infatti:
1
1
 r1  mv1
 rmv 1  rmR
Lz 
1z 
2
2
 r2  mv2 v1  R
v2
v2  R
 rmv 2  rmR

2
 rmR cos  rmR  cos  2mR 
2
2z
Il momento angolare trasverso, in questo caso
F1t
particolare, in cui i due momenti angolari sono
allineati, vale:
F1c
L  1  2  rmR  sen  rmR  sen  2rmR  sen
Nel caso del manubrio asimmetrico Lx ed Ly non sono nulli,
anzi non sono neppure costanti perché il momento angolare
precede attorno all’asse di rotazione:
L
1

2
 rmR   rmR  rmR   L  
Mz  0    cos tan te
 L  cos tan te
2z
1z
1
I
•
•
R
F2c
 r2
O
F2t
    90
r1
v1
dL x
 Mx  0
dt
dL y
 My  0
dt
G.M. - Informatica B-Automazione 2002/03
Calcolo del momento delle forze esterne
quando L non è parallelo all’asse di rotazione
•
Supponiamo che il momento angolare sia costante in
modulo
z
– Vuol dire che Mz=0, =costante
•
•
Prendendo l’origine di L sull’asse di rotazione, la punta
di L descrive una traiettoria circolare in un piano
perpendicolare all’asse di rotazione.
La variazione subita da L nell’intervallo dt è data da:
•
dL
 M  dL  Mdt
dt
Il suo modulo
dL  M dt
•
Dalla figura
M   L sen
•
d

dL
L

costante
dL  Lsend  dL  Lsen dt

L 
M  
2
Affinché il momento angolare L preceda attorno all’asse di rotazione occorre
applicare un momento delle forze, e quindi delle forze, la cui intensità è
proporzionale al quadrato della velocità angolare.
G.M. - Informatica B-Automazione 2002/03
Manubrio asimmetrico
•
•
•
Riusciamo a capire il motivo dell’esistenza di questi
momenti ?
Facendo riferimento alla figura, osserviamo che per
mantenere sulla traiettoria circolare i due punti materiali
che formano il nostro manubrio occorre applicare a
ciascun punto materiale una forza centripeta.
Le due forze sono uguali in intensità ma di verso
opposto e non sono allineate.
z, asse di rotazione
v2
R

2
– Formano una coppia di momento diverso di zero
– Esse quindi non possono essere delle forze interne, come
nel caso simmetrico, perché sappiamo che il momento
risultante delle forze interne è nullo.
F1c
– Devono essere fornite dall’esterno.
– Normalmente sono i vincoli a cui è affidato il compito di
mantenere fisso l’asse di rotazione, che si occupano di
esercitare delle forze che svolgono lo stesso ruolo delle
forze centripete menzionate.
– Naturalmente anche l’intensità di queste forze aumenta
con l’aumentare della velocità angolare
2z
1z
1
F2c
 r2
O
    90
r1
v1
G.M. - Informatica B-Automazione 2002/03
Equilibratura
•
•
•
•
•
Poiché queste forze non hanno nessun altra funzione che
quella di far precedere il momento angolare attorno
all’asse di rotazione
Per esempio non hanno alcuna influenza sulla velocità
angolare
Ma al tempo sottopongono a sforzi inutili tutta la
struttura (l’asse di rotazione, i cuscinetti, etc)
Si preferisce lavorare in modo che il momento angolare
sia parallelo all’asse di rotazione (in cui tali forze non
sono richieste)
Questo si ottiene “equilibrando” il corpo rigido rispetto
all’asse di rotazione (equilibrature delle gomme
dell’automobile)
z, asse di rotazione
v2

v1
G.M. - Informatica B-Automazione 2002/03
•
Un cilindro di massa 2 kg può ruotare attorno al proprio asse (longitudinale)
passante per O. Nel piano della sezione rappresentata nella figura sono
applicate quattro forze, aventi le intensità F e le distanze r dal centro riportate
in tabella. Trovare l’intensità e il verso dell’accelerazione angolare del
cilindro, ammettendo che, durante il moto, le forze mantengano la
orientazione rispetto al cilindro.
Applicaz
ione
F1  6.0N F2  4.0N F3  2.0N F4  5.0N
R1  5.0cm R 2  12.0cm
M z  I
•
L’equazione del moto:
I
1
1
2
2
2
MR  2kg.12m  0.0144kgm
2
2
F1
M z1  F1R 2  6N  .12m  0.72Nm
F2
M z2  F2 R2  4N  .12m  0.48Nm
F3
M z3  F3R1  2N  .05m  0.10Nm
F4
M z4  0
Mz  .72  0.48  0.10  .14Nm

Mz
.14Nm
rad


9.7
2
2
I
0.0144kgm
s
•
L’accelerazione è diretta in verso
antiorario
G.M. - Informatica B-Automazione 2002/03
•
Una riga di lunghezza L=1m, è messa in posizione verticale, appoggiata al
pavimento e quindi lasciata cadere. Trovate la velocità dell’estremità superiore
quando colpisce il pavimento, ammettendo che l’estremità inferiore non slitti
•
•
•
•
Applicaz
ione
Possiamo considerare la riga come una sbarretta sottile.
Il moto di caduta può essere immaginato come un moto di
rotazione attorno ad un asse passante per il punto di contatto
O.
Le forze agenti sono la forza peso, la normale e la forza di
attrito (statico) che mantiene fermo il punto di contatto.
Possiamo applicare la conservazione dell’energia:
E  Wn c 
WN  WFa
0
0
p erch è ap pl. p un to fermo
Ei  Ef  K i  Ui  K f  Uf
U=0
L 1 2
0  mg  I  0
2 2
L
2
2  mgL  3g
 
1
1
I
mL 2 L
2
3
P
mg
 
3g
L
N
Fa O
3g
m
v  L 
L  3gL  5.42
L
s
G.M. - Informatica B-Automazione 2002/03
•
Un corpo rigido è formato da tre asticelle sottili identiche di lunghezza L, unite
tra loro in modo da assumere una forma ad H come mostrato in figura.
L’insieme è libero di ruotare intorno ad una asse orizzontale fosso che coincide Applicaz
con una delle gambe della H. Partendo da una posizione di riposo in cui il
ione
piano della H è orizzontale, il sistema è lasciato libero di cadere.
Qual è la velocità angolare del corpo quando il piano della H arriva in
posizione verticale?
•
•
•
Rv
Proviamo ad applicare la conservazione
dell’energia
Le forze agenti sono il Peso e la reazione
vincolare applicata dall’asse di rotazione:
E  Wn c 
P
0
WR v
0
p erch è ap pl. p un to fermo
Asse di rotazione
Ei  Ef  K i  Ui  K f  Uf
0  MgL 
2 
1 2
L
I  Mg
2
2
L
2  MgL
1
I
I
2
Mg
M  3m
•
U=0
Dobbiamo calcolare il momento di inerzia
dell’H rispetto all’asse di rotazione
G.M. - Informatica B-Automazione 2002/03
•
•
Un corpo rigido è formato da tre asticelle sottili identiche di lunghezza L, unite
tra loro in modo da assumere una forma ad H come mostrato in figura.
L’insieme è libero di ruotare intorno ad una asse orizzontale fosso che coincide Applicaz
con una delle gambe della H. Partendo da una posizione di riposo in cui il
ione
piano della H è orizzontale, il sistema è lasciato libero di cadere.
Qual è la velocità angolare del corpo quando il piano della H arriva in
posizione verticale?
I  I1  I 2  I3
I
•
I1  0
1 2
I 2  mL
3
2
I 3  0  mL
I1
1
4
2
2
2
mL  mL  mL
3
3
I3
La velocità angolare vale dunque:

I2
 
2
MgL 3mgL
9g


4 2 4L
I
mL
3
9g
4L
G.M. - Informatica B-Automazione 2002/03
Moto di puro rotolamento
• Con questo moto si intende il moto caratteristico
delle ruote
– Quando un veicolo si muove, anche le ruote si
muovono.
– Naturalmente il moto delle ruote non è di pura
traslazione
– Né una semplice rotazione attorno ad un asse fisso
– Può essere immaginato come un moto di
rototraslazione
• Qual è la peculiarità di questo moto?
– I punti della ruota a contatto con l’asfalto sono fermi rispetto all’asfalto
(non scorrono, non strisciano sull’asfalto)
– Da qui il nome: rotolamento senza strisciamento (oppure puro rotolamento).
• Consideriamo due istanti successivi t1 e t2.
– Lo spostamento subito dal centro della ruota x è pari alla distanza tra i
punti di contatto della ruota agli istanti t1 e t2.
– Nello stesso tempo la ruota avrà subito anche uno rotazione e quindi uno
spostamento angolare .
• Se il moto è di puro rotolamento esiste una relazione tra questi due
spostamenti:
x  R 
Condizione di puro rotolamento
G.M. - Informatica B-Automazione 2002/03
Le condizioni di puro rotolamento
•
Abbiamo stabilito che in condizioni di puro rotolamento
vale la seguente relazione tra i moduli dello spostamento
angolare e quello lineare.
x  R 
•
Con il sistema di riferimento scelto osserviamo che se x
è positivo, come in figura, allora  è negativo (rotazione
oraria)
Tenendo conto dei segni la condizione di puro
rotolamento diventa:
x  R
•
v x  R
•
Dividendo per t, e valutando il limite per t che tende a zero: si ottiene:
•
La velocità lungo l’asse x del centro della ruota (CM) è uguale all’opposto del
prodotto del raggio della ruota per la sua velocità angolare.
ax  R
Con una seconda derivazione, si ottiene
•
•
L’accelerazione lungo l’asse x del centro della ruota (CM) è uguale all’opposto
del prodotto del raggio della ruota per la sua accelerazione angolare.
•
•
Queste tre condizioni sono verificate contemporaneamente (dipendono l’una dall’altra)
Esse vengono indicate come “condizioni di puro rotolamento”
N.B.:Il segno meno presente nelle condizioni di puro rotolamento dipende dal sistema
di riferimento usato. Una diversa scelta del SdR potrebbe
chiedere
tale segno 2002/03
G.M. non
- Informatica
B-Automazione
•
•
•
•
•
Ruolo della forza di attrito nel moto di
puro rotolamento
Nel moto di puro rotolamento il punto di contatto della
ruota con l’asfalto è fermo rispetto all’asfalto.
Il compito di mantenere fermo rispetto al piano di appoggio
il punto (o i punti) di contatto è affidato alla forza di attrito
Naturalmente si tratta di una forza di attrito statica proprio
perché il punto di contatto non scivola sulla superficie di
appoggio
Senza attrito questo tipo di moto non è realizzabile (al massimo è possibile un
moto uniforme: velocità del centro di massa costante e velocità angolare costante, non
appena si vuole cambiare una delle due velocità e fare in modo che il moto continui ad
essere di puro rotolamento è necessaria la presenza della forza di attrito)
Naturalmente, poiché la forza di attrito statico è limitata superiormente, non
sempre è garantito il moto di puro rotolamento.
– Si pensi alle frenate brusche fatte con l’automobile in cui si bloccano le ruote che
scivolano sull’asfalto
– Oppure alle accelerazioni brusche in cui le ruote girano, ma slittano sull’asfalto e
non producono l’avanzamento dell’automobile.
– Occorre verificare caso per caso se la forza di attrito statico sia sufficiente per
garantire il moto di puro rotolamento
•
Si osservi infine che la forza di attrito statico compie lavoro nullo (punto di
applicazione fermo). (Lo stesso vale anche per la Normale).
G.M. - Informatica B-Automazione 2002/03
Interpretazione del moto di puro
rotolamento
•
Pura rotazione attorno ad un asse perpendicolare alla figura
passante per i punti di contatto.
– L’asse di rotazione cambia continuamente (si parla di asse
istantaneo di rotazione.
– Comunque istante per istante il moto di ogni punto della ruota è
uguale a quello che avrebbe se la ruota ruotasse attorno ad un
asse fisso passante per i punti di contatto.
•
Sovrapposizione di un moto di traslazione
– Moto del centro di massa
più un moto di rotazione attorno ad un asse perpendicolare
alla figura e passante per il centro di massa
•
•
Il moto della ruota nel
sistema del centro di
massa è una rotazione
attorno ad un asse fisso.
La velocità angolare è
la stessa di quella
misurata nel sistema
inerziale.
G.M. - Informatica B-Automazione 2002/03
•
•
•
Una forza orizzontale costante di 10 N è applicata a una ruota di massa
M=10kg e raggio R=0.30 m, nel modo come indicato in figura. La ruota rotola
senza strisciare sulla superficie orizzontale, e l’accelerazione del suo centro di
massa è 0.60 m/s2.
Quali sono l’intensità ed il verso della forza di attrito sulla ruota
Qual è il momento di inerzia della ruota intorno all’asse di rotazione passante
per il suo centro?
Applic
azione
G.M. - Informatica B-Automazione 2002/03
Moto di puro rotolamento di un cilindro
•
•
Consideriamo un cilindro di massa M e raggio R che si
può muovere su di un piano orizzontale sotto l’azione di
una forza F applicata nel suo centro di massa.
Le altre forze agenti sul cilindro sono
– La forza peso applicata al centro di massa
– La normale N applicata nel punto di contatto
– La forza di attrito anch’essa applicata nel punto di contatto.
•
y
F
N
Fas
x
P
Sia la normale N che la forza di attrito statico sono distribuite su tutti i punti
della generatrice del cilindro a contatto con il piano
– Facendo ricorso a questioni di simmetria possiamo renderci conto che l’insieme di
queste forze è equivalente ad un’unica forza applicata nel punto di mezzo del
segmento costituito dai punti contatto tra cilindro e piano orizzontale
– Nella figura le forze risultanti, sia per quanto riguarda la Normale che per la forza di
attrito statico, sono state applicate proprio nel punto precedentemente determinato
(esso si trova infatti sulla sezione del cilindro che contiene il centro di massa).
•
NB: in generale non si può stabilire a priori il verso della forza di attrito statico
– Ragioni di simmetria ci dicono che deve essere parallela alla forza applicata F, però
potrebbe andare verso destra o verso sinistra.
•
In figura abbiamo scelto a caso (quasi) uno dei due versi: se risolvendo il problema
determiniamo un modulo negativo, non vuol dire che abbiamo raggiunto un risultato
assurdo, solo che abbiamo sbagliato la scelta del verso che, pertanto, andrà corretta.
G.M. - Informatica B-Automazione 2002/03
Risoluzione del moto di rotolamento come
pura rotazione attorno ai punti di contatto
y
M z  I
•
L’equazione del moto è:
•
•
•
I è il momento di inerzia rispetto all’asse di rotazione
Mz è il momento assiale risultante delle forze applicate.
Nel nostro caso:
F
M z  FR
P
Mz  0
N
Mz  0
Fas M z  0
•
2
Steiner
N
Fas
x
P
1
3
2
2
2
MR  MR  MR
2
2
FR  I
Utilizzando la condizione di puro rotolamento
a
 FR  I x
R
•
I  I *  Mh 
F
FR 2
ax 
I
NB:non abbiamo avuto alcuna informazione sulla
forza di attrito.
ax  R
FR 2
FR2
2F
ax 
3

I
MR2 3M
2
G.M. - Informatica B-Automazione 2002/03
Risoluzione del moto di rotolamento come
sovrapposizione del moto del centro di massa più
una rotazione attorno al centro di massa
•
Dal teorema del centro di massa: F  P  N  Fas  Ma CM
y
x F  Fas  Ma CM x
y N  Mg  Ma CM y  0
•
F
N  Mg
L’equazione del moto di rotazione attorno ad un asse
*
*
fisso nel SdR del CM:
Mz  I 
F
N
Fas
Mz  0
Traslazione
F  Fas  Ma CM x
P
Mz  0
Rotazione
 Fas R  I 
N
Mz  0
con dizion e di p uro ro tolamento
a CM x  R
*
a
Fas  I CM2 x
R
*
ax 
F
I*
M 2
R

F I
*
Fas M z  FasR
a CMx
2  Ma CMx  a CMx 
R
F
F
2F


1
1
MR2 M  M 3M
2
M 2 2
R
x
P
I 
*
1
2
MR
2
Fas R  I 
*
F
I*
M 2
R
1
F
*a
2 2F
Fas  I CM2 x  MR

2
R
2
3MR
3
F
puro rotol. 
  sN  s Mg
3
G.M. - Informatica B-Automazione 2002/03
Dove è finita l’energia
N
N
F
Fas
•
F
P
P
ax 
Con attrito
– Moto di puro rotolamento
•
•
•
ax 
Senza attrito
– Pura traslazione
F
M
Se la forza opera per un tratto x: v f  vo  2ax x
2
2
vf
•
2F
3M
2F
2
x
3M
Solo i due terzi del quadrato della
velocità del caso senza attrito
Bisogna considerare anche l’energia
cinetica del moto di rotazione
K  K f  Ki 
0
2
F
 2 x
M
1
1
F
2
K  K f  Ki  Mvf  M2 x  Fx  WF
2
2
M
0
2
vf
1
1 * 2 1
11
1
2F  1 
2
2
2 2
Mvf  I  f  Mv f 
MR  f  M2
x1    Fx  WF
2
2
2
22
2
3M
2
v2
f
3

G.M. - Informatica B-Automazione
2002/03
2
•
•
•
•
Una forza orizzontale costante di 10 N è applicata a una ruota di massa
M=10kg e raggio R=0.30 m, nel modo come indicato in figura. La ruota rotola
senza strisciare sulla superficie orizzontale, e l’accelerazione del suo centro di
massa è 0.60 m/s2.
Quali sono l’intensità ed il verso della forza di attrito sulla ruota
Qual è il momento di inerzia della ruota intorno all’asse di rotazione passante
per il suo centro?
Applic
azione
Dal teorema del centro di massa: F  P  N  Fas  Ma CM
N
x F  Fas  Ma CM x
y N  Mg  Ma CM y  0
y
N  Mg
x
Fas  F  Ma CMx  10 10  .60  4N
•
per la rotazione
Mz  I 
*
*
F
Mz  0
P
Mz  0
N
Mz  0
Fas M z  FasR
F
I 
*
Fas
1
2
MR
2
Fas R  I 
R 2 Fas .32  4 .36
I 


 0.6kgm 2
a CM x
0.60
0.60
*
P
ax  R
Fas  I
*
a CM x
2
R
*
G.M. - Informatica B-Automazione 2002/03