Analisi Dati
(Explorer & Nautilus)
Gruppo P
Sabrina D’Antonio
Ottobre 2004
3 - 4 Ottobre 2003
2003
IdfIdF
2004
Nautilus
LNF: 41º.82 N - 12º.67 E
Azimuth = 44º E
Explorer
CERN: 46º.45 N - 6º.20 E
Azimuth = 39º E
Elaborazione del Segnale
Vp
Rp
Cd
h
Antenna
M
L0
Filtro
Li
V
Oscillatore
Massa M
Temperatura T
Fattore di Qualità Q
Frequenza f0
Trasduttore
Efficienza
Amplificatore
Temperatura di Rumore Tn
=
E. elettrica
E. meccanica
Dati Sperimentali …
V
campionato ad intervalli di tempo di
12.8 ms (Nautilus) e 6.4 ms (Explorer)
Filtro
progettato per segnali di tipo δ
rivelazione di bursts brevi:
- impulsi di durata ~ 1 ms;
- segnali a frequenza variabile che
intercettano le risonanze delle barre
ricerca sensibile
a O.G. emesse
nei collassi gravitazionali
durante gli stadi finali della
coalescenza di sistema binari
(NS-NS, NS-BH, BH-BH)
… Dati Sperimentali
Segnale filtrato s (t) normalizzazione, tramite la calibrazione del
rivelatore, tale che s2 rappresenti l’energia d’oscillazione (in Kelvin)
Rumore : moto termico degli oscillatori amplificatore
distribuzione di s (t) è normale con media = 0
s2
f (s) exp 2 Teff
temperatura
efficace
Segnale d’Uscita
Sciame di raggi cosmici su NAUTILUS
Quadrato del
Segnale d’Uscita
dell’Amplificatore
(V2)
Segnale
d’Uscita
del Filtro
(T)
Eventi …
soglia in Rapporto Critico :
CR =
|s| - ‹|s|›
σ (|s|)
= 6
moving average
Et = 19.5 Teff
(media di |s| nei 10’ precedenti)
|s| > soglia considero s solo se nella sua evoluzione temporale
tornato al disotto della soglia vi rimane per più di 3 s
Evento
{ smax , t (s = smax )}
…Eventi
EVENTO
Amax
T(Amax)
Inizio
evento
Fine
evento
… Eventi
Eventi cercati : segnale di O.G. (energia Es) + rumore
rumore gaussiano probabilità teorica di rivelare segnale con
rapporto segnale-rumore (SNR) pari a Rs = Es / Teff
P
0.856
Rt = 19.5
Probabilità 48% (14%)
di NON rivelare segnale
con Rs = 20 (30)
0.522
Rs
Ampiezza del Segnale
Modello per il segnale di O.G. : impulso di durata τg
(per orientazione
ottimale: θ = /2 )
1
h =
4 L f02
1
τg
kB Es ½
M
Es. - Nautilus & Explorer
τg = 1 ms
h 2 x 10-19
Es ½
1 mK
Sensibilità
picco di calibrazione
Larghezza
di banda
Δf
½
Tn
Sensibilità
di picco
½
T
MQ
Explorer & Nautilus 2001
Explorer
•
•
•
•
•
ON da Marzo a Dicembre
Larghezza di Banda = 9 Hz
T = 2.6 K
f0 = 904.7, 921.3 Hz
Sensibilità Media
h = 4.5 x 10-19
Nautilus
•
•
•
•
•
ON da Gennaio a Dicembre
Larghezza di Banda = 0.4 Hz
T = 1.5 K
f0 = 906.97, 922.46 Hz
Sensibilità Media
h = 5.7 x 10-19
Funzionamento in coincidenza per 213.5 giorni
Selezione degli Eventi
A. Eliminati eventi in coincidenza (entro 5 s) con i segnali
d’uscita dei sismometri - 8%
Definite:
Teff (1h) = ‹ s2 › in 1 ora di funzionamento continuo
Teff (10m) = ‹ s2 › nei 10’ precedenti l’evento
B. Considerati solo eventi con: Teff (1h) 10 mK ; Teff (10m) 7 mK
C. Considerati solo eventi a periodi di durata > 1h
A B C : ancora eventi di grande energia
rumore extra (in aggiunta a quello termico
ed elettronico) che è necessario eliminare
Coincidenze
Coincidenze
Eventi nei 2 rivelatori la cui distanza temporale | Δt | w
Analisi: confronto tra il n. di tali eventi (nc) e il n. di coincidenze
accidentali (nf), i.e. il n. di coincidenze che si verificano per caso
N.B. - fissato un tempo di misura T durante il quale 2 rivelatori registrano,
rispettivamente, N1 e N2 eventi (distribuiti uniformente), il n. di
coincidenze accidentali entro un ritardo w è dato da N1 N2 w / T
Misura delle accidentali: traslazione temporale relativa
delle sequenze degli eventi dei 2 rivelatori
100 shifts con passo | Δtsh | = 2 s
ciascuno, da –100 s a +100 s
calcolo del n. di coincidenze nsh
nf =
1
100
nsh (k)
Σ
100 k
1
Finestra Temporale
Come è scelta w ?
segnali simulati rumore reale caratterizzazione della distribuzione
del tempo dell’evento intorno all’istante di applicazione del segnale
Segnali Impulsivi
1
1
σd = 0.28
Δf Re½
da simulazioni
SNR evento
Nautilus Explorer : σc2 = σNau.2 + σExp.2
N.B. - σc σNau.
w = 3 σc
0.5 s
Analisi Statistica delle
Coincidenze
Limitata ai soli eventi di coincidenza verificatisi durante
periodi di acquisizione dati continua di durata 12 h
Distribuzione Temporale
NO sorgenti di O.G. nel Sistema Solare & insufficiente sensibilità
dei nostri rivelatori per eventi extragalattici eventuali segnali
devono provenire dalla nostra Galassia (ipotesi “a priori”)
opportuna variabile temporale è il tempo siderale
Distribuzione Energetica
Coordinate Terrestri
ψ = Longitudine
φ = Latitudine
asse rotazione
terrestre
O = Osservatore
O
G
φ
C
ψ
Equatore Terrestre
(ET)
G = Greenwich
C = Centro Terra
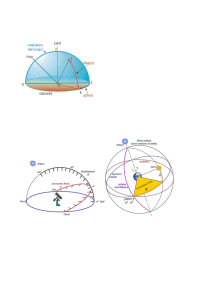
Coordinate Orizzontali Locali
z
Z
A = azimuth
h = altezza
Sfera Celeste
P
O
y Est
Asse z = verticale locale
Z = zenit
h
A
O = Osservatore
x
Nord
Orizzonte Celeste
(HC)
Coordinate Equatoriali Locali
z
H = angolo orario
δ = declinazione
PN
Sfera Celeste
Z
O = Osservatore
P
O
y Ovest
δ
H
x
Sud
Equatore Celeste
(EC)
Asse z = linea dei poli
PN = polo Nord
N.B. – δ indipendente da posizione
e istante di osservazione
Coordinate Equatoriali Assolute
= ascensione
δ = declinazione
PN
Sfera Celeste
P
x
O
δ
O = Osservatore
y
Sud
Equatore Celeste
(EC)
= punto vernale
punto fisso intersezione dell’eclittica con Ec (quella in corrispondenza del
passaggio del Sole dall’emisfero Sud a quello Nord: equinozio di primavera)
Confronto tra Sistemi di Coordinate
HC
Z
EC
O
C
C = Centro Terra
O = Osservatore
Z = zenit di O
φ
ET
ET = equatore terrestre
EC = equatore celeste
HC = orizzonte celeste
asse rotazione
terrestre
Tempo Siderale …
angolo orario del punto vernale
Z
per un generico
oggetto, risulta:
O
N
tsid. = H + α
H
S
α
HC
EC
… Tempo Siderale
Terra e Sole all’equinozio
di primavera
Posizioni A e B sfera
celeste appare identica
all’osservatore: è trascorso
un giorno siderale
Giorno siderale dura meno
di quello solare medio:
A
B
Δt =
24
h = 3’ 56”.56
365.2564
N.B. – dopo 1 anno, tempo solare e siderale sono di nuovo in fase
gg. (anno siderale) = gg. (anno solare) + 1
Ora siderale 4.2
Distribuzione in Tempo Solare
Tempo Solare (h)
Fondo
Conteggi
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
1.50
1.33
1.15
0.88
0.95
1.32
1.21
0.99
0.92
0.48
0.61
0.77
0.65
1.32
1.51
1.50
0.97
0.85
1.15
1.10
0.87
0.91
0.93
1.22
2
2
1
0
0
2
2
1
1
1
2
1
0
2
1
2
1
1
1
3
1
0
2
2
Totali
25.09
31
3.5
Fondo
Conteggi
3.0
2.5
2.0
1.5
1.0
0.5
0.0
0
2
4
6
8
10
12
14
Tempo Solare (h)
16
18
20
22
24
Distribuzione in Tempo Siderale
Tempo Siderale (h)
Fondo
Conteggi
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
0.61
0.97
1.11
0.92
0.77
0.65
0.59
0.58
0.65
0.98
0.50
0.67
1.44
1.71
2.23
0.93
1.03
1.27
1.32
0.88
1.68
1.45
1.04
1.09
2
1
0
4
3
1
1
1
0
1
0
1
1
2
3
0
1
1
2
1
2
1
1
1
Totali
25.07
31
4.5
Fondo
Conteggi
4
3.5
3
2.5
2
1.5
1
0.5
0
0
2
4
6
8
10 12 14 16
Tempo Siderale (h)
18
20
22
24
“Probabilità” Poissoniane
eccesso nell’intervallo di ora siderale [ 3, 5 ) è significativo ??
• nc eventi di segnale variabile di Poisson con media nc
• nf eventi di fondo variabile di Poisson con media nf
quantifico il grado di confidenza nell’ipotesi di esistenza di un
segnale calcolando quanto probabile risulta l’osservazione di
un numero di eventi nc in presenza del solo fondo
P (nf, nc) =
p (μ; m) =
Σn n
μm e-μ
m!
nc - 1
p (nf ; n) = 1 c
Σ0 n p (nf ; n)
funzione di distribuzione di
Poisson
Distribuzione Temporale di P(nf, nc) …
Tempo Solare (h)
P (nf, nc)
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
0.4422
0.3838
0.6834
1.0000
1.0000
0.3802
0.3410
0.6284
0.6015
0.3812
0.1252
0.5370
1.0000
0.3802
0.7791
0.4422
0.6209
0.5726
0.6834
0.0996
0.5810
1.0000
0.2385
0.3446
Solare
1
0.1
0.01
0
2
4
6
8
10
12
14
Tempo Solare (h)
16
18
20
22
24
… Distribuzione Temporale di P(nf, nc)
Tempo Siderale (h)
P (nf, nc)
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
0.1252
0.6209
1.0000
0.0145
0.0432
0.4780
0.4457
0.4401
1.0000
0.6247
1.0000
0.4883
0.7631
0.5099
0.3853
1.0000
0.6430
0.7192
0.3802
0.5852
0.5005
0.7654
0.6465
0.6638
Siderale
1
0.1
0.01
0
2
4
6
8
10
12
14
Tempo Siderale (h)
16
18
20
22
24
Osservazioni su P(nf, nc)
1. NON è la probabilità dell’ipotesi {H0: assenza di segnale}, ma la
probabilità che assunta H0 si ottengano almeno nc eventi
2. ? non i valori delle variabili di Poisson con i relativi errori
Esempio: bin tsid. [ 3, 4 ) nf = 0.92, nc = 4 n = 3.08
stima di n = 3.08 4 + 0.92 3.1 2.2
(i.e. n è compatibile con 0 entro 1.5 σ )
non è quello che ci interessa: ha a che fare con la probabilità che,
fluttuando, una variabile con media nc diminuisca fino nf
Siamo interessati, invece, alla probabilità che, fluttuando, una
variabile Poissoniana con media nf aumenti fino nc, i.e. P (nf, nc)
Log-Likelihood
(opposto del) logaritmo del prodotto delle
probabilità (poissoniane) dei singoli bins
della distribuzione in esame
24
L=-
Σi
1
ln p (nf (i) ; nc (i) )
Tempo Solare (h)
Log-Poisson
Tempo Siderale (h)
Log-Poisson
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
1.3822
1.4528
1.0102
0.8800
0.9500
1.4579
1.5219
1.0001
1.0034
1.2140
2.2917
1.0314
0.6500
1.4579
1.0979
1.3822
1.0005
1.0125
1.0102
2.6058
1.0093
0.9100
1.7683
1.5154
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.5
18.5
19.5
20.5
21.5
22.5
23.5
2.2917
1.0005
1.1100
4.4316
3.3459
1.0808
1.1176
1.1247
0.6500
1.0002
0.5000
1.0705
1.0754
1.3302
1.6158
0.9300
1.0004
1.0310
1.4579
1.0078
1.3356
1.0784
1.0008
1.0038
Log-Likelihood
30.6156
Log-Likelihood
32.5905
Distribuzione Cumulativa della Log-Likelihood …
1. Generazione di N (~ 106) distribuzioni sperimentali “simulate”
ottenute estraendo per ogni bin (i = 1,24) una variabile random
poissoniana con valor medio = nf(i) nc(i)
2. Calcolo della Log-Likelihood per ciascuna di queste distribuzioni
“simulate”
f (L) = funzione di distribuzione della log-likelihood
distribuzione della cumulativa di f (L)
L
dL
F (L) =
f (L)
Lmin
Lmax
L dL
min
f (L)
… Distribuzione Cumulativa della Log-Likelihood
0.718
0.444
Significatività Statistica
•
P-value della cumulativa della Log-Likelihood: nell’ipotesi
di solo fondo, probabilità di ottenere casualmente un valore
di L del valore sperimentale
Solare:
P = 1 – 0.444 = 0.556
Siderale: P = 1 – 0.718 = 0.282
•
Likelihood Ratio Test
LSol. = exp (- LSol.)
LSol.
LSid. = exp (- LSid.)
LSid.
= exp ( LSid. - LSol. ) 7.21
i.e. probabilità che la distribuzione sperimentale in tempo
solare sia compatibile con il fondo è ~ 7 volte più grande
della corrispondente probabilità per quella in tempo siderale
N.B. - no info sulle probabilità assolute !!
Energia degli Eventi in tsid. [ 3, 5 )
tsid. (h)
E. EXPLORER (mK)
E. NAUTILUS (mK)
3.1
3.4
3.7
4.0
4.1
4.5
4.6
96.10
178.93
63.00
101.76
87.02
193.60
94.25
130.32
195.36
56.64
133.23
93.03
225.63
128.16
Energia NAUTILUS (mK)
250
200
150
100
50
0
0.00
50.00
100.00
150.00
Energia EXPLORER (mK)
200.00
Fit Lineare …
(a, b) tali che risulti minima la
somma dei quadrati dei residui
Fit Lineare: ŷk = a + b xk
N
S=
Σk ( yk – ŷk )2
1
‹ y › ‹ x2 › – ‹ x › ‹ x y ›
a=
‹ x2 › – ‹ x ›2
N
‹ x › = N-1
Σk xk
1
‹xy›–‹x›‹y›
b=
‹ x2 › – ‹ x ›2
N
‹ y › = N-1
Σk yk
1
N.B. - ‹ x2 › – ‹ x ›2 = σx2
N
‹ x y › = N-1 Σk xk yk
1
… Fit Lineare
per le energie degli eventi delle 2 antenne con tsid. [ 3, 5 ), risulta:
Retta:
a = 7.1722 mK
b = 1.1197
Energia NAUTILUS (mK)
250
200
EN 7.17 + 1.12 EE
150
100
50
0
0.00
50.00
100.00
150.00
Energia EXPLORER (mK)
200.00
Distribuzione dei Residui
relazione lineare tra le 2 variabili residui Δyk = yk – ŷk sono
aspettati essere distribuiti random intorno all’asse Δy =0
30
Retta (mK)
Residui (mK)
96.10
178.93
63.00
101.76
87.02
193.60
94.25
114.7304
207.2154
77.7722
121.0502
104.5921
223.5953
112.6648
15.5896
-11.8554
-21.1322
12.1798
-11.5621
2.0347
15.4952
0.7496
20
Residui (mK)
EE (mK)
10
0
50
100
150
-10
-20
-30
Energia EXPLORER (mK)
Però con pochi punti (< 10) la distribuzione dei residui
non è significativa: può emergere struttura casuale
200
Coefficiente di Correlazione Lineare
Covarianza di 2 variabili random:
1
cov (x,y) =
N
N
Σk ( xk - ‹ x › ) ( yk - ‹ y › )
1
= ‹ x y › - ‹ x › ‹ y › = b σx2
ρ=
cov (x,y)
σx σy
σx
= b σ
y
coefficiente di
correlazione
N.B. - si dimostra che | ρ | 1
(EE , EN) coefficiente di correlazione campionario:
R = 0.9651
Verifica di Ipotesi Statistiche
Procedura mediante la quale, a partire dal campione
osservato, si decide di rifiutare (non rifiutare) un’ipotesi
statistica H0 (ipotesi nulla) riferita alla popolazione
definizione di una statistica, i.e. v.c. S : (X1, …, Xn) R
identificazione di una regione critica Ω0 nell’insieme dei
possibili valori s assunti da S al variare del campione
Decisione
s Ω0
H0 è rifiutata
s Ω0
H0 è accettata
rispettando il vincolo:
P ( s Ω0 | H 0 ) = α
livello di significatività
Test d’Ipotesi su R
R è compatibile con l’ipotesi { H0 : ρ = 0 } ?
Assunzione : coppia di v.c. normali
Statistica test
(Fisher)
S =
R
½
(N
–
2)
~ T(N – 2)
2
½
(1 – R )
Student con N - 2 g.d.l.
| S | t (α / 2; N - 2)
α = 0.05
N=7
R = 0.9651
t (0.025; 5) = 2.57
S = 8.24
rifiuto H0
ipotesi
d’indipendenza
delle 2 variabili
è da rifiutare
Test “distribution-free” …
Caso generale: (EE , EN) non è v.c. normale bivariata
accoppiamento casuale di tutti gli eventi dei 2 rivelatori
17090 coincidenze gruppi da 7 eventi per
ciascuno dei quali si calcola R
R
… Test “distribution-free”
Distribuzione cumulativa di R
0.9944
F (R)
Il valore sperimentale
R = 0.9651 viene
superato solo nello
0.56 % dei casi
0.9651
R
la correlazione osservata dei 7 eventi è molto poco compatibile con
l’ipotesi che essi appartengano all’insieme delle coincidenze accidentali
Conclusioni …
Osservato un eccesso di coincidenze nell’intervallo di ora siderale
[3,5), proprio quando il piano di max. sensibilità dei rivelatori è || al
disco galattico (per sorgenti concentrate nel centro galattico
avremmo dovuto trovare anche un eccesso all’ora siderale 13.6)
Si tratta di nc – nf ~ 6 coincidenze in 5 giorni (2 ore siderali su
24, in un totale di ~ 60 giorni). In termini di conversione
d’energia abbiamo ~ 1 ev./g con un energia di ~ 100 mK
burst con h ~ 2 x 10-18 conversione in O.G. di ~ 4 x 10-3 M o·
con sorgenti localizzate ad una distanza di 8 kpc
rate osservata » di quella prevista da qualunque
modello teorico per le sorgenti galattiche di O.G.,
ma non in contrasto con gli attuali modelli di
formazione ed evoluzione della Galassia
… Conclusioni
La significatività statistica di tale eccesso non consente di fare
affermazioni conclusive circa la natura dei segnali osservati, anche
se riteniamo (cfr. la correlazione in energia) improbabile che esso
sia dovuto a fluttuazioni di rumore
Sebbene gli eventi non siano dovuti a sciami di raggi cosmici, non
possiamo completamente escludere la possibilità che essi siano
associati a qualche altro (ancora ignoto) fenomeno esotico
… occorre continuare a raccogliere dati e
migliorare le prestazioni dei rivelatori (i.e. SNR)