Fisica 2 10° lezione

Magnetostatica 1
6 giugno 2011
Magneti
Campo magnetico
Azione della corrente elettrica su un magnete
Azione di un magnete sulla corrente elettrica
Forza su un filo percorso da corrente (seconda formula di
Laplace)
Forza su una carica in moto (forza di Lorentz)
Moto di una carica in un campo B uniforme
Magneti
• Ogni magnete ha due regioni (poli) in cui la forza che
esercita è più intensa
• Nell’interazione tra due magneti, poli omonimi si respingono
e poli eteronimi si attraggono
• L’azione delle forze magnetiche si pensa sia mediata,
similmente al caso elettrico, da un campo, il campo
magnetico, indicato con la lettera B e di natura vettoriale
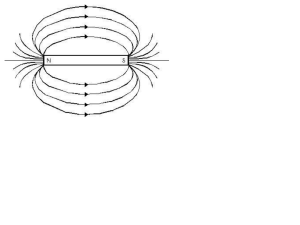
• Le linee di campo escono dal polo nord e entrano nel polo
sud
• L’esistenza di un campo magnetico viene rivelata
sperimentalmente mediante l’azione su di un altro magnete
“esploratore”, in genere di forma molto allungata (ago
magnetico) con i poli disposti alle estremità
2
Campo magnetico
• L’intensità del campo varia con la
distanza dal magnete
• Un’indagine quantitativa ha stabilito
che la forza tra poli di aghi molto
allungati, varia come l’inverso del
quadrato della distanza
• La direzione orientata del campo è
quella secondo cui si dispone l’ago
magnetico esploratore
• Il verso del campo è da sud a nord
dell’ago esploratore
B
N
S
3
La Terra come magnete
• La Terra è un magnete
naturale con i poli magnetici
vicini ai poli geografici
• Il polo di un magnete che
punta verso il nord terrestre
prende il nome di polo nord
• Similmente il polo che punta
verso il sud terrestre prende il
nome di polo sud
• Quindi il polo nord magnetico
terrestre è in realtà un polo sud
magnetico e viceversa il polo
sud magnetico terrestre è in
realtà un polo nord magnetico
4
Magnetostatica
• Parrebbe che si potesse introdurre il concetto di
carica magnetica e i poli sarebbero la sede di
queste cariche
• I poli magnetici, come cariche magnetiche,
sarebbero del tutto analoghi alle cariche
elettriche, grazie anche alla dipendenza della
forza tra poli magnetici dall’inverso del quadrato
della distanza
5
Magnetostatica
• Vista la legge di forza, in magnetostatica
varrebbero allora le stesse leggi che in
elettrostatica
int
int

(
B
)

4

k
Q
 ( E )  4keQe
e
m
C(E)  0
C ( B)  0
• La differenza tra ‘cariche’ magnetiche e cariche
elettriche è che le prime non si presentano mai
singolarmente, ma, apparentemente, sempre in
coppie di tipo opposto
6
Poli e cariche magnetiche
• Se si spezza un magnete, ai due lati della rottura si
crea una coppia di poli (opposti), in modo che
ciascuno dei due pezzi e` un nuovo magnete
completo
• Non è mai stata osservata una carica magnetica
isolata (monopolo). Le equazioni della fisica dei
magneti sono quindi
 ( B )  4k e Qmint  0
C ( B)  0
• Per studiare un campo B si e` quindi costretti ad
usare un magnete esploratore, su cui sono
contemporaneamente presenti entrambi i poli
7
Momento agente su un ago in un
campo B esterno
• Un ago magnetico in un campo B esterno è soggetto ad
una coppia il cui momento può essere misurato
• La situazione è analoga a quella di un dipolo elettrico in
un campo E
• Possiamo definire un nuovo ente vettoriale: il momento
magnetico m dell’ago
– direzione e verso sono individuati dal vettore che va dal polo S
al polo N dell’ago
– il modulo m è tale che quando l’ago è posto in un campo B, la
coppia risultante ha momento meccanico
 
  m B

• L’energia dell’ago in un campo esterno è, analogamente
 
al caso elettrico,
E  m  B
8
Campo magnetico di un ago
• In certi sistemi si possono comunque considerare
formalmente i poli magnetici come se fossero cariche
magnetiche
• In particolare questo è vero proprio per il campo
generato da un ago magnetico, che costituisce l’analogo
del dipolo elettrico e viene per questo detto dipolo
magnetico
• I due campi hanno allora la medesima forma: p e` il
momento di dipolo elettrico e m il momento (di dipolo)
magnetico
2cos

p 
E  ke 3  sin  
r0 

 0 
2cos

m 
B  km 3  sin  
r0 

0


9
Azione della corrente elettrica su
un magnete
• Le forze magnetiche non
agiscono solo fra magneti
• 1800: Volta inventa la pila
• 1819: Oersted osserva che
una corrente elettrica agisce
cambiando la direzione di un
ago magnetico
• Ciò viene interpretato
dicendo che un circuito
percorso da corrente genera
un campo magnetico nello
spazio circostante
• È l’inizio del processo che
porterà all’unificazione di
elettricità e magnetismo,
ovvero all’elettromagnetismo
Forze di tipo nuovo
• La forza tra magnete e corrente è il primo
esempio di forza non newtoniana
• 1876: l’esperienza di Rowland sottolinea
questa peculiarità, mostrando la
dipendenza della forza dalla velocità
11
Azione di un magnete sulla
corrente elettrica
• Viceversa anche un magnete agisce
su una corrente
• Sperimentalmente si trova che la forza
con cui un campo magnetico uniforme
agisce su una corrente in un filo
rettilineo
– È proporzionale all’intensità della corrente i
– È proporzionale alla lunghezza l del filo
immerso nel campo
– È proporzionale al seno dell’angolo tra la
direzione del campo e della corrente
– È perpendicolare sia al campo che alla
direzione della corrente
• Chiamiamo B la costante di
proporzionalità
i
F
q
l
F  il sin 
F  Bil sin 
12
Campo magnetico
• Quindi la forza si può scrivere così (regola della mano
destra)
  
F  il  B
• Il vettore B definisce completamente il campo magnetico
o di induzione magnetica
• Grazie a questa forza, si può usare anche un circuito
“esploratore” percorso da corrente per rivelare un campo
magnetico
13
Seconda legge di Laplace
• Possiamo pensare il filo come un insieme di
tratti infinitesimi
• Su ciascuno agirà una forza infinitesima
 

dF  idl  B
• Possiamo ora generalizzare la legge di forza ad
un filo di forma arbitraria e ad un campo
magnetico qualsiasi
 

F  i  dl  B
14
Dimensioni e unità di misura di B
• L’equazione
precedente definisce
implicitamente B
• Le dimensioni di B
sono
• L’unità di misura è il
tesla (T)
• Si usa anche il gauss
(G), ereditato dal
sistema cgs em
  
F  il  B

F  F T
B 

i L QL
Ns
T
Cm
1G  10 4 T
15
Principio di sovrapposizione
• Consideriamo diversi magneti o circuiti percorsi
da corrente, ciascuno dei quali genera un
campo magnetico
• Il campo magnetico risultante è dato dalla
somma vettoriale dei singoli campi
n 

Btot   B j
j 1
• Questa proprietà è una verità sperimentale
16
Azione di B su una carica in moto
• La forza agente su di un filo si può pensare come risultante delle
forze elementari agenti su ognuna delle cariche in moto che
costituiscono la corrente
• La corrente i può scriversi i  qnAv d
• Siccome in un filo rettilineo l e vd hanno la stessa direzione
possiamo riscrivere
 
 la forza così


F  qnvd Al  B  qnAl vd  B
• E dato che nAl rappresenta il numero di portatori nel volume di

sezione A e lunghezza l
 
F  nAl qvd  B
• Siamo indotti a concludere che su una singola carica agisce la

 
forza (di Lorentz)
f  qv  B
• Mentre B agisce su una corrente elettrica o su una singola carica in
moto, non c’è interazione tra un magnete e una carica ferma
17
Forza di Lorentz
• La forza magnetica è sempre
perpendicolare alla velocità della particella
• Quindi non compie lavoro e non fa variare
l’energia cinetica
• Fa variare la direzione della quantita` di
moto, ovvero della velocità, ma non il loro
modulo
18
Moto di una carica in un campo
uniforme
• 1) La velocità iniziale sia
ortogonale al campo
• La forza di Lorentz fornisce la
forza centripeta
• r è il raggio di curvatura locale
• Dato che il modulo della velocità
è costante, anche r è costante
• La traiettoria è quindi un cerchio
nel piano perpendicolare a B
mv2
 evB
r
mv
r
eB
• 2) Se v ha una componente vp parallela al campo,
questa non introduce forze aggiuntive e si ha solo
un moto rettilineo uniforme con velocità vp lungo la
direzione del campo
• La traiettoria risultante è un’elica
19
Differenza tra linee del campo
elettrico e magnetico
• La forza elettrica ha la direzione delle linee di campo
• La forza magnetica ha direzione perpendicolare alle linee
di campo
• Le linee di campo elettrico (statico) originano da cariche
positive e terminano su cariche negative
• Le linee di campo magnetico non originano da né
terminano su punti dello spazio, perché non esistono
cariche magnetiche isolate
• Le linee di campo magnetico sono perciò linee chiuse e il
flusso attraverso una superficie
chiusa e` nullo

( B)  0
• Legge di Gauss per il campo B, ovvero assenza di
cariche magnetiche
• E’ la terza equazione dell’e.m.
20
Flusso del campo B



 
 B | S   B  dA
• Definizione
S
• Dimensioni fisiche
 B   BL2
• Unità di misura è il weber (Wb)
u( B )  u( B)m2  Tm2  Wb
21