Diapositiva 1 - INFN

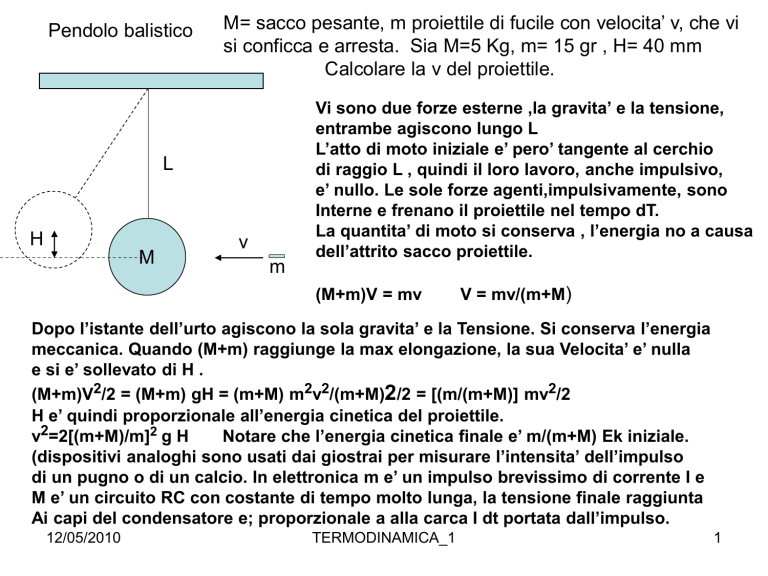
Pendolo balistico
M= sacco pesante, m proiettile di fucile con velocita’ v, che vi
si conficca e arresta. Sia M=5 Kg, m= 15 gr , H= 40 mm
Calcolare la v del proiettile.
L
H
M
v
m
Vi sono due forze esterne ,la gravita’ e la tensione,
entrambe agiscono lungo L
L’atto di moto iniziale e’ pero’ tangente al cerchio
di raggio L , quindi il loro lavoro, anche impulsivo,
e’ nullo. Le sole forze agenti,impulsivamente, sono
Interne e frenano il proiettile nel tempo dT.
La quantita’ di moto si conserva , l’energia no a causa
dell’attrito sacco proiettile.
(M+m)V = mv
V = mv/(m+M)
Dopo l’istante dell’urto agiscono la sola gravita’ e la Tensione. Si conserva l’energia
meccanica. Quando (M+m) raggiunge la max elongazione, la sua Velocita’ e’ nulla
e si e’ sollevato di H .
(M+m)V2/2 = (M+m) gH = (m+M) m2v2/(m+M)2/2 = [(m/(m+M)] mv2/2
H e’ quindi proporzionale all’energia cinetica del proiettile.
v2=2[(m+M)/m]2 g H
Notare che l’energia cinetica finale e’ m/(m+M) Ek iniziale.
(dispositivi analoghi sono usati dai giostrai per misurare l’intensita’ dell’impulso
di un pugno o di un calcio. In elettronica m e’ un impulso brevissimo di corrente I e
M e’ un circuito RC con costante di tempo molto lunga, la tensione finale raggiunta
Ai capi del condensatore e; proporzionale a alla carca I dt portata dall’impulso.
12/05/2010
TERMODINAMICA_1
1
v
S
V = costante
Resistenza dell’aria?
Dimensionalmente : massa auto,densita’aria,
Sezione frontale,velocita’, forma……..
F ~ ρ S V2
Nel tempo T avanza di X = VT spazzando il volume SVT e spostando
Una massa di aria M = ρ SVT = ρ SX.
L’aria deve essere spinta di lato di un tratto <Y> ~ k S1/2 nel Tempo T=x/V
La velocita’
<y>/T = k S1/2 V/x e l’energia cinetica
Ek = ½ ρ SX k2 S V2 /X2 = ½ ρ S k2 S V2 /X
Moltiplicando e dividendo per X
Ek = ½ ρ S V2 Cx X
Dove Cx = k2 S/X2 e’ un a quantita’ adimensionale che dipende dalla forma
Ek e’ energia cinetica dissipata = lavoro della Fattrito per percorrere X =
Lavoro fatto dal motore per mantenere la V costante
Ek = Fa X
e quindi
Fa = ½ ρ S V2 Cx
[ m l2 l2 /l3 t2] = [mlt-2]
La potenza e’ lavoro nell’unita’ di tempo = Ek/T = F v = ½ ρ S V3 Cx
12/05/2010
TERMODINAMICA_1
2
y
a
x
F
dX
θ1
x
F
a e’ una perturbazione che si propaga
Lungo la corda. Sia Y= Y(x) la sua
Forma. F e’ la tensione ai capi di dx.
Il moto di dx e’ lungo Y sotto l’azione
θ2 Della forza
Fy = F ( sinθ2- sin θ1)~ F( tg θ2- tg θ1)
tg θ2 = dY/dx (x=x+dx) e tg θ1= dY/dx (x=x)
( tg θ2- tg θ1) = d2Y/dx2 dx
Fy = F d2Y/dx2 dx = “may” = ρ dx d2Y/dt2
d2Y/dx2 = ρ/F d2Y/dt2
Questa equazione ha soluzioni del tipo f = f (X)= f (wt – kx) e rappresenta
Un’onda che si propaga . Infatti il valore f (0) per X = 0 si ottiene per tutte
Le copie (x,t) che soddisfano la condizione wt-kx=0 cioe’ x = w/k t
Dove V= w/k e’ la velocita’ di “propagazione” della “forma” f.
Si noti che [w] = [t-1] e [k]=[x-1] quindi w rappresenta una frequenza e t una
Lunghezza (d’onda o altro).
Poiche’ d2f/dx2 = k2 d2f/dX2 e d2f/dt2 = W2 d2f/dX2 l’equazione e’ anche
d2f/dx2 = (k/w)2 d2f/dt2
e
V2 = ρ/F
12/05/2010
TERMODINAMICA_1
3
Su una corda tesa e inestensile: gli unici parametri fisici sembrano essere la densita’ lineare λ della
corda e la sua tensione T (la lunghezza e’ ininfluente e supposta infinita, la gravita trascurabile (cioe’
la tensione e’ >> λg)
[λ] = m/l
[T] = ml/t2
[v2] = T/λ
Tensioni elevate o λ piccole = v alta = frequenza elevata o lungh. d’onda corta.
Masse elevata o T bassa = frequenze basse o lungh. d’onda lunga
In un fluido incomprimibile (es. acqua) : l’ampiezza A , ρ, la lunghezza d’onda L, g …………
l’ampiezza A potrebbe essere importante, ma probabilmente e’ A/h (profondita’) che e’ importante e
se h >>A l’ampiezza dovrebbe essere irrilevante.
A parita’ di ρ la velocita’ sara’ v2 ~ Lg cioe’ w/k = L1/2/g1/2 l’onda lunga e’ piu’ veloce.
L’onda si disperde perche’ le alte frequenze corrono meno ,rimangono indietro…….
Se pero’ A diventasse importante (cioe’ A/h non infinitesimo) si potrebbe ottenere V2 = Ag
E questo e’ interessante perche’ non ci sarebbe dipendenza da L (nessuna dispersione) e l’onda
potrebbe propagarsi con velocita’ elevata dipendente dalla sua ampiezza. (solitoni,onde solitarie e
Tsunami)
12/05/2010
TERMODINAMICA_1
4
1) Si considera un insiem di N molecole “indistinguibili”
1) N molto grande e le molecole prive di volume
2) No forze esterne (gravita’ trascurabile) ne’ interne tra le molecole
3) Urti tra molecole e con pareti perfettamente elastici
4)Posizioni e velocita’ completamente casuali
(ogni molecola ha la stessa prob. di trovarsi nell’intorno dP di qualsiasi punto
P(xyz) o nell’intorno dV della velocita’ V (vx,vy,vz).
V e’ un cubo di lato L , fermo o in moto rettilineo e uniforme . Il sistema di rif. e’
solidale a L.
Se il numero di molecole per unita’ di L e’ N/L , quello nella regione dx e’
Dn = dx N/L= N dx/L .La probabilità’ di una molecola di trovarsi in dx e’ dx/L.
X
L
dx
12/05/2010
Se P e’ la prob. di ogni cittadino di trovarsi alle 12 al
Canton del Gallo e N e’ il numero totale di cittadini che
possono andare al CdG, il loro numero alle 12 al CdG
e’ n = NP. La probabilita’ che un cittadino qualsiasi sia
al CdG alle 12 e’ dunque n/N . Essa e’ il rapporto tra il
numero degli eventi favorevoli e tutti quelli possibili
solo se tutti gli eventi sono equiprobabili [Cardano 1560medico,matematico e giocaore d’azzardo].
TERMODINAMICA_1
5
Dx
X
L
n
Vix e’ positiva se la molecola i va verso l’alto, negativa se
va verso il basso. Poiche’ i due casi sono equiprobabili la
velocita’ media lungo X <Vx> = S Vix/N = 0 (idem <Vy>
e <Vz>).
Ma la media <Vx2> di Vix2 e’ diversa da zero e uguale
a <Vy2> e <Vz2>.
La media del quadrato delle velocita’
<v2>= SVi2 / N = <Vx2>+<Vy2>+<Vz2> = 3<Vx2>
Una molecola che urti elasticamente la parete con Vix cede la qdm 2mVix.
Se DT e’ il tempo tra due urti molecolari successivi, una molecola con Vix urtera’ la
parete con velocita’ Vix se la sua distanza dalla parete e’ minore di Dx = Vix DT.
La probabilita’ di una molecola di trovarsi in Dx e’ Dx/L = Vix DT/L . Poiche’ Vix puo’
essere + o – la probabilita’ che si muova verso la parete e’ la meta’ VixDT/(2L).
Questa e’ la probabilita’ che una molecola con velocita’ Vix urti la parte con Vix nel
tempo DT.
Nell’urto elastico la molecola cede l’impulso I(ix) = 2m Vix. Quindi l’impulso medio
(probabile) ceduto e’ il suo valore I(ix) volte la probabilita’ dell’urto VixDT/2L .
Che da’ <I(ix)> =m Vix2DT/L
L’impulso totale si ottiene sommando su tutte le i , la Forza dividendo per DT
F = S Vix2 m/L e la pressione P = F/L2 = S Vix2 m / L3
Poiche’ S Vix2 = <Vx2> N = <V2> N/3
PV = Nm <v2>/3
12/05/2010
TERMODINAMICA_1
6
L’energia cinetica media di una molecola e’ <Ek> = ½ m<v2>
Quindi
PV = 2/3 N <Ek>
Sperimentalmente l’equazione di stato di n moli di gas perfetto monoatomico
In equilibrio termodinamico
PV= nRT = N/Na RT = NRT/Na
Una mole di gas contiene Na molecole quindi n = N/Na
Da PV = 2/3 N <Ek>
Si ha <Ek> = 3/2 kT
con K = R/Na
K = 1,38 x 10 -23 J/K
Na =6 x 10 26 /kg mole oppure 6x1023 /gmole
La massa molecolare e’ la massa in unita’ atomiche (n nucleoni)
Idrogeno = 1u
Ossigeno = 16 u
1 u = 1,67 x 10-27 kg = massa prot.
Una quantita’ in grammi pari alla massa molecolare contiene 6x 10 23 molecole
Una mole di gas perfetto a 1 Atm e 273 K (0 gradi cent.) occupa 22,414 litri
12/05/2010
TERMODINAMICA_1
7
L’equazione PV= nRT oppure PV = 2/3 N <Ek> dove <Ek> = 3/2 kT e’
L’energia cinetica media di ogni molecola e’
“ l’equazione di stato dei gas perfetti monoatomici”
Poiche’ una molecola monoatomica ha tre gradi di liberta’ ½ kT e’ <Ek>/grado di liberta’ .
Una molecola biatomica ha 5 gradi di liberta’ ,quindi <Ek> = 5/2 kT etc…..
Queste relazioni valgono in condizioni di equilibrio :
all’equilibrio termodinamico ogni sottovolume contenente un numero sufficientemente
elevato di molecole da consentire la definizione di una pressione e di una temperatura
ha la stessa pressione e temperatura e le sue molecole possiedono la stessa <Ek>.
Lo stato termodinamico di un gas e’ definito quando siano definiti i valori di (P,V,T) .
Un gas in equilibrio termodinamico possiede una energia interna U :
U e’ funzione dello stato termodinamico., quindi di P,V,T.
U varia quando il gas cambia il proprio stato interagendo con l’ambiente.
Ogni interazione presuppone infatti uno scambio di energia: il gas puo’ assorbire
o cedere energia . Questo avviene scambiando calore o lavoro con l’ambiente.
Lavoro = movimento di parti mobili sotto l’azione del sistema (gas o altro).
Si consideri un gas chiuso all’interno di un cilindro dotato di un pistone mobile.
L’energia interna U aumenta se il gas assorbe calore attraverso le pareti del cilindro e
diminuisce se il gas compie lavoro sull’esterno (p.es. muovendo il pistone e aumentando
il proprio volume. Il gas compie un lavoro positivo). Diminuisce se cede calore
e aumenta se l’esterno compie lavoro sul gas (p.es. comprimendolo riducendone il volume
con uno spostamento del pistone.Il gas compie un lavoro negativo).
12/05/2010
TERMODINAMICA_1
8
Q
p
Q
p
W
W
lavoro
Q
calore
W
Q
Q
p
pressione
p
p
W
W
P e’ SEMPRE la pressione del gas sul pistone :
Se viene fatto lavoro sull’esterno Wgas > 0 ma il contributo ΔU alla variazione
dell’energia interna U e’ negativo.
Se l’esterno fa lavoro sul gas, W gas < 0 , ma il contributo ΔU a U e’ positivo.
Il calore Q da’ un contributo positivo quando e’ fornito al gas, negativo quando e’
ceduto.
L’espressione Δ U = Q - W , o piu’propriamente dU = δ Q – δ W
e’ il “primo principio della termodinamica “ .
E’ basato su risultati sperimentali e contiene due concetti :
A) Il calore e’ una forma di energia (principio di equivalenza calore-lavoro)
B) L’energia di un sistema isolato si conserva sempre.
12/05/2010
TERMODINAMICA_1
9
p
A
B
V
P,V,T
S
vuoto
P’,V’,T’
12/05/2010
dW = F ds = P dV . Il W da A a B lungo i vari cammini
e’ l’area compresa tra il cammino e l’asse V.
Essa dipende dal cammino. La variazione finita di U
e’ Δ U = U(B) – U(A) indipendente dal percorso.
dU e’ il differenziale esatto di una U(P,V,T).
Poiche’ W dipende dal cammino, il primo princ. dice
che anche Q dipende dal percorso.
dW e dQ non sono differenziali esatti di una funzione
di P,V,T
Le pareti non conducono il calore, il setto S si rompe
e il gas occupa tutto il volume: esso non ha scambiato
ne’ calore, ne’ lavoro con l’ambiente.
Per il primo principio Δ U = 0 – 0 = 0
P e V sono cambiate , l’unica variabile che
sperimentalmente non cambia e’ T.
Quindi U di un gas perfetto dipende solo da T.
In effetti l’energia cinetica media delle molecole non
e’ cambiata , esse si muovono solo in un ambiente
piu’ grande. Se invece S si fosse messo in movimento,
le molecole urtandolo sarebbero rimbalzate
con velocita’ minore e diminuendo la propria Ek ( e T).
TERMODINAMICA_1
10
E‘ possibile aumentare di ΔT la temperatura di una massa m gas fornendogli calore.
Si considerano due casi : a volume costante e a pressione costante.
Il calore necessario a volume costante e ‘
Q = m Cv Δ T
m = massa del gas
La pressione del gas aumenta.
P1 V = nRT1
P2V= nRT2
ΔU = Q – 0 = mCv (T2-T1)
La quantita’ di calore necessaria per uno stesso aumento Δ T a P = cost sia Q’ = m Cp Δ T
Per aumentare la temperatura a P = cost bisogna aumentare il volume , il gas deve
compiere lavoro dW= PdV.
Δ U = Q’ – W
W = P Δ V = nR Δ T (P=cost)
Δ U = (mCp – nR) Δ T = m Cv Δ T
Cp = Cv + R > Cv
Cp e Cv = calori specifici a volume e pressione costante .
Per un gas perfetto sono delle costanti, indipendenti dallo stato del sistema.
Una trasformazione (ideale) puo’ avvenire in modo quasi statico : in ogni istante il
sistema e’ in equilibrio termodinamico interno e con l’esterno (l’universo) e quindi
possiede valori P,V,T definiti. La trasformazione puo’ essere descritta da curve
continue in diagrammi (P,V), (T,V), (P,T) o (P,V,T).
Una trasformazione quasi statica e’ reversibile se un cambio infinitesimo dei parametri
fa percorrere al sistema lo stesso cammino in verso opposto.
Una trasformazione reversibile e’ quasi statica , il reciproco non e’ necessariamente vero.
12/05/2010
TERMODINAMICA_1
11
12/05/2010
TERMODINAMICA_1
12
Le trasformazioni piu’ comuni nei sistemi fisici sono:
isoterme ,
PV= cost T = cost
dU = dQ – dW = 0
dQ= dW= PdV
adiabatiche, dQ= 0
dU = 0 – dW
dU + dW = dU + PdV = 0
L’equazione di una adiabatica quasi statica/reversibile PVγ = cost
γ = Cp/Cv
Trasformazione adiabatica:
dU + P dV =0
dU puo’ essere rappresentata come dU = Cv dT e P = RT/V
R= Cp – Cv
Cv dT + (Cp-Cv) T dV/V = 0 dT/T = - (Cp-Cv)/Cv x dV/ V
ln T = - (γ -1) ln V + cost.
TV (γ -1) = cost
poiche’ T=PV/R
oppure W  nRT ln
12/05/2010
PV γ = cost x R = Cost
pf
pi
TERMODINAMICA_1
13
=-
12/05/2010
TERMODINAMICA_1
14
Velocita’ del suono in aria : dimensionalmente m,P,V,T massa/ Vol. = ρ densita’
La densita’ dipende da T , quindi per data T, restano P e ρ , quindi
v  P/
oppure
dP / d
Bisogna tener conto di dP e dρ perche’ il mezzo e’ un gas che e’ comprimibile.
ρ = 1.29 g/cm3 = 1,29 Kg/m3
Se il processo e’ isotermo PV = cost P/ρ =cost = 105 / 1.29
d (Pρ-1) = 0 = dP ρ-1 – P ρ-2 d ρ da cui dP/d ρ = P/ ρ
P = 10 5 N/m2
V= 278 m/sec
Se il processo e’ adiabatico
PVγ = cost e
dP/dρ = γ P/ρ
La molecola d’aria e’ biatomica Cv= 5/2 R
e Cp =7/2 R
γ= Cp/Cv =1.4
V = 278 x 1,41/2 = 329 m/sec
12/05/2010
TERMODINAMICA_1
15
V
dV
U
A
V’
V’’
Dx
V1
V2
Il volume V ha sezione A e lunghezza Dx .Viene compresso nel tempo dt dal pistone
U con velocita’ u che ne riduce il volume di dV. Il Volume V’ si riespande comprimendo
V2 in V’’ etc…Questo provoca il movimento dell’onda di pressione lungo X con
velocita’ v = Dx/dt. Dopo il movimento il pistone si ferma : nel tempo dt ha ceduto un
certo impulso I alle molecole del gas in V . Mentre il pistone percorre u dt il fronte di
pressione ha percorso Dx e la velocita/media molecolare che era 0 ha acquistato una
componente non nulla lungo x a causa dell’impulso esercitato dal pistone .
Questa componente viene fulmineamente ceduta alle molecole di V2 etc…(urto elastico)
La massa compressa dal pistone e’ Δm = ρ A dx =ρ A vdt
Se il pistone si e’ mosso con velocita’ u, le molecole hanno acquistato la QdM
Q = Δm u = ρ A v u dt = Impulso = Fdt = Δ P A dt da cui Δ P = ρ v u
d ρ/ ρ = dV/V
ρ = d ρ / (dV/ V)
dV = A u dt
V = A v dt dV/ V = u / v
e dP = v2 d ρ
dP
v
12/05/2010
d
TERMODINAMICA_1
16
Come ottenere lavoro dal calore?
In una espansione isoterma tutto il calore fornito e’ trasformato in lavoro dW= PdV , ma
poi bisogna riportare il sistema alle condizioni iniziali , possibilmente spendendo meno
energia di quella ottenuta nell’espansione.
P C
D
Qh
B
Qc
V2
A
V1
Un motore a scoppio : CICLO DI OTTO
AB e CD sono adiabatiche , BC e DA isocore
In AB la miscela viene compressa e T passa da
TA a TB (il lavoro fatto sul gas e’ l’area sotto AB).
Nella fase di esplosione V rimane essenzialmente
costante ma il calore della combustione provoca
un aumento di T e P.Nella successiva espansione
CD il gas compie lavoro e la sua T e P scendono.
Nella fase DA il gas e’ sostituito con gas miscela
fredda , equivale ad un raffreddamento a V costante.
Le linee punteggiate sono per indicare trasformazioni che possono essere non
quasi statiche e reversibili e quindi non rappresentabili in un diagramma PV
In BC e DA il lavoro e’ nullo (V=cost)
Qh (> 0) = dU = nCv (TC – TB) calore assorbito
Qc(<0) = nCv (TD-TA)
Alla fine del ciclo in A ,stato finale= stato iniziale dU = 0 = (Qh –Qc) – W
Il rendimento e’ il rapporto tra l’energia assorbita e il lavoro prodotto
η = W/Qh = (Qh-Qc)/Qh = 1 – Qc/Qh = 1 – (TD-TA)/(TC-TB)
12/05/2010
TERMODINAMICA_1
17
Si e’ fatto uso solo del primo principio, se le trasformazioni fossero quasi statiche
si potrebbero usare le equazione delle trasformazioni adiabatiche e ottenere un
risultato piu’ preciso .
Adiabatiche
TV (γ-1) =cost
TA V1 (γ-1) = TB V2 (γ-1) e anche TD V1 (γ-1) = TCV2 (γ-1) sottraendo si ha
(TD-TA)/ (TC-TB) = (V2/V1) (γ-1) = TA/TB = TD/TC
η = 1-TA/TB = 1- TD/TC
La macchina scambia calore durante le isocore a varie temperature delle quali TA e’ la
piu’bassa e TC la piu’ alta.
Lavoro lungo una trasf. Adiabatica reversibile da T1 a T2
12/05/2010
TERMODINAMICA_1
W = nCv (T2- T1)
18
CICLO DI CARNOT : si puo’ fare meglio usando due temperature: Th e Tc
C
Qc
Il ciclo consiste di due isoterme (AB e CD)
alle temp, Tc e Th con Tc< Th. e due
adiabatiche (BC e DA).
+ Qc
D
W
AB) dU = 0 = -Qf - Wab Wab = - Qf
BC) dU = 0 – Wbc = U(Tc) – U ( Tf)
B
- Qf
A
Qf
W = Qc – Qf
CD) dU = 0 = Qc – Wcd
Wcd = Qc
DA) dU = 0 – Wda = U (Tf) - T(c)
η = (Qc-Qf)/Qc = 1 – Qf/Qc
tende a 1 se Qf tende a zero.
Si supponga il ciclo reversibile : il lavoro fatto dal gas nelle isoterme si ha integrando
PdV dove P puo’ essere ricavato dall funzione di stato P = nRT/V
PdV=nRT dV/V
e W = nRT Ln (Vf / Vi)
Qc = nRTc (ln Vd/Vc) e Qf = nRTf ln (Vb / Va) . Nelle connessioni adiabatiche
Usando la TV(γ-1) = cost si ha (Vb / Va)(γ-1) = (Vc / Vd) (γ-1)
Vb / Va=Vc / Vd
E quindi Qf/Qc = Tf /Tc
e
η = 1- Tf /Tc dove Tf e Tc sono le temperature
estreme. Il rendimento e’ superiore al Ciclo di Otto .
Si ouo’ dimostrare che il ciclo di Carnot tra Th e Tc e’ quello che ha il rendimento
massimo tra tutti i cicli possibili tra le due temperature.
12/05/2010
TERMODINAMICA_1
19
Il ciclo di Carnot, come tutti i cicli puo’ essere percorso in verso opposto:spendendo
il lavoro W e’ pssibile trasferire Qf dalla sorgente fredda
cedendo Qc = Qf + W alla sorgente calda (frigorifero) .
C
AD) dU= 0 – Wad Wad = - nCv (Tc-Tf)
Qc
DC) dU=0 = -Qc – Wdc
Wdc= -Qc
-Qc
D
CB) dU = 0 – Wcb Wcb = nCv (Tf-Tc)
W
BA) dU = 0 = Qf – Wba Wba = Qf
B
Winverso= (Qf – Qc) = - W diretto
Qf
A
Qf
Si definisce una efficienza
k = Qf / W = Qf/(Qf-Qc) > 1
K tende a infinito quando Qf tende a Qc
(e W tende a 0)
Queste due situazioni illustrano i risultati sperimentali alla base del secondo principio
della termodinamica, del quali si danno due enunciati :
A) Kelvin : non e’ possibile ottenere lavoro continuativo trasformando tutto il calore
prelevato da un solo serbatoio alla temperatura T . Una parte dell’energia prelevata
deve essere ceduta a un serbatoio a temperatura piu’ bassa.
B) Clausius : non e’ possibile il trasferimento continuo di energia da un serbatoio a
temperatura piu’ bassa ad uno a temperatura piu’ alta senza spendere lavoro.
12/05/2010
TERMODINAMICA_1
20
Enunciato di Kelvin
Qf
≠
una macchina viola Kelvin e fa
funzionare all’inverso una
seconda macchina.
La macchina complessiva
trasferisce calore da freddo
A caldo senza lavoro esterno
inverso e viola Clausius
12/05/2010
0
Enunciato di Clausius Winverso ≠ 0
Una macchina viola Clausius e
trasferisce con Winverso nullo dal
serbatoio freddo a quello caldo il Qf
ceduto al serbatoiio freddo da una
altra macchina . La macchina
Complessiva viola Kelvin perche’
Produce lavoro con Qf = 0
TERMODINAMICA_1
21
Una macchina qualsiasi m’ ha un rendimento η’ maggiore di η di m Carnot tra
le stesse temperature.
η’ = 1- Q’f/Q’c > 1 – Qf/Qc = η
Q’f/Q’c < Qf/Qc
m e’ reversibile e lavorando all’inverso Qf – Qc – W =0 trasferisce Qc a Tc
con il lavoro W = Qf – Qc.
m’ puo’ prelevare Q’c = Qc cedendo al serbatoio a Tf il calore Q’f < Qf e
Compiendo il lavoro Q’c – Q’f –W’ = 0
W’ = Q’c – Q’f
Poiche’ Q’c = Qc e Q’f< Qf
W’ > ! W !
Complessivamente la macchina non scambia calore con Tc, sottrae a Tf
Qf- Q’f e compie il lavoro W’ – W violando Clausius.
Nessuna macchina tra Tc e Tf ha un rendimento superiore alla macchina reversibile di Carnot.
Una macchina reversibile qualsiasi ha η’ > η Carnot
Q’c =Qc
W’
W
Q’c
Qc
W’
Q’f
Qf
Q’f <Qf
12/05/2010
Se η’ > η Q’f < Qf e la macchina
sottrae Qf-Q’f senza lavoro, quindi
la macchina reversibile η’ non puo’
avere rendimento superiore alla
macchina a gas perfetto di Carnot
TERMODINAMICA_1
22
Si possono riformulare i due enunciati del secondo principio (che fanno riferimento
a macchine e trasformazioni particolari) in modo piu’ generale in termini di una
grandezza “astratta” : l’entropia S.
se δ Q e’ il calore scambiato dal sistema REVERSIBILMENTE alla temperatura T
e si definisce dS =δ Q/T allora la variazione di S di una qualsiasi macchina che
compia un qualunque processo ciclico e’
 dS   Q / T
Si consideri un ciclo di Carnot dQ = 0 lungo le adiabatiche ,lungo l’isoterma a Tc
ΔSc = Qc/Tc
lungo quella a Tf
ΔSf = - Qf/Tf
ma Qf/Qc = Tf/Tc
Quindi
ΔS = ΔSc + ΔSf = Qc/Tc - Qf/Tf = 0
 dS   Q / T  0
cio’ implica che S e’ una funzione di stato del sistema : la variazione di S del
sistema per un QUALUNQUE processo che porti un sistema da A a B e’
ΔS = S(B) – S(A) ed e’ ovviamente nulla per qualsiasi processo ciclico.
La variazione S(B) – S(A) dell’entropia del sistema puo’ essere calcolata
lungo QUALUNQUE processo reversibile che porti da A a B.
12/05/2010
TERMODINAMICA_1
23
S e’ per definizione una grandezzza additiva e puo’ essere calcolata per
Qualunque scambio di calore. In un ciclo il calore viene assorbito e ceduto ad
una serie di serbatoi a varie temperature Ti. Un serbatoio e’ un oggetto con una
capacita’ termica abbastanza elevata da rendere la sua variazione du temperatura
dTi trascurabile quando assorbe o cede la quantita’ di calore Qi.
Nel caso di un sistema termodinamico che passi da A a B compiendo il lavoro
complessivo W e scambiando le quantita’ di calore Qi , la variazione totale
di S e’ la somma della variazione della macchina con quella della variazione dei
serbatoi Ti
Q
Stot  Smacch  i i
Nel caso di un ciclo
Smacch  0
Ti serbatoi
Q
Stot  i i
Ti serbatoi
Nel caso di un ciclo di Carnot la ΔS del serbatoio Tc e’ ΔSc= -dQc/Tc (Tc cedeQc) e
ΔSf =dQf/Tf (Tf assorbe Qf ) e Qc/Qf= Tc/Tf .
ΔS serbatoi = 0
12/05/2010
TERMODINAMICA_1
24
Poiche’ qualsiasi ciclo reversibile puo’essere
approssimato dall’esecuzione di n cicli di Carnot
La variazione totale di entropia per un qualsiasi
ciclo reversibile e’ nulla .
Per una espansione isoterma ΔS puo’ essere calcolato lungo una isoterma e
reversibile . Il sistema assorbe Q a T da un serbatoio a T e compie W=Q.
ΔSsist= Q/T >0
ΔSserb = - Q/T
ΔStot = 0
L’opposto e’ vero in una compressione, il sistema cede –Q e il serbatoio
assorbe Q.
In una adiabatica dQ = 0
12/05/2010
ΔStot = 0
TERMODINAMICA_1
25
Si consideri un processo irreversibile : es espansione libera .
E’ un processo isotermo senza scambi di calore con l’embiente ΔS ambiente =0
Per calcolare la ΔS sist si puo’ usare una isot reversibile dallo stato iniziale
PoVo a PfVf . Perche’ questo avvenga il gas compie il lavoro PdV
W =∫PdV = RTdQ/ dV/V
dQ-dW = 0
dW=dQ
ΔS = R ln Vf/Vo >0
poiche’ U non e’ cambiata
dS= dQ/T=dW/T=RdV/V
ΔStot > 0
Altra causa di irreversibilita’ puo’ essere il passaggio di calore Qc da un serbatoio
a Tc a uno a T’c < Tc attraverso un sistema K che non cambia stato.
Qc
Tc
K
T’c
M
12/05/2010
La macchina M compie una isot. Rev : ΔStot = 0
ΔSk = 0 (K non cambia stato)
ΔStc = -Qc/Tc ΔSTt’c = Qc/T’c
ΔStot = Qc/T’c – Qc/Tc > 0
W
TERMODINAMICA_1
26
In qualsiasi processo termodinamico la variazione totale di entropia di siatema
piu’ ambiente e’ sempre maggiore o uguale a zero.
Essa e’ uguale a zero solo se tutte le trasformazioni sono reversibili, qualunque
causa di irreversibilita’ si traduce in un aumento della S totale.
La Macchina M lavora tra un serbatoio a Tc in un ambiente, cui cede calore,
A To<Tc. Il suo rendimento
W/Q=1-To/Tc
W = Q(1-To/Tc)
Tc
M
La frazione (1-To/Tc) di Q viene utilizzata per W
La frazione To/Tc e’ inutilizzabile e ceduta all’ambiente
a To. Si osservi che E inut.= To Q/Tc
Si introduca un serbatoio intermedio a T’c<Tc.
Il passaggio di Qc da Tc a T’c e’ ovviamente irreversibile
To
Tc
T’c
Il lavoro ottenuto e’ ora W’ = Q(1-To/T’c) < W
La frazione non utilizzabile e’ ora To/T’c > To/Tc
E’ inut = Q To/T’c.
E’-E = To (Q/T’c – Q/Tc) >0
E inut. e’ aumentata!!!
M
E’-E = To ΔS irr.
To
12/05/2010
TERMODINAMICA_1
27
In qualunque processo cicclico reversibile . (quindi con il max rendimento possibile)
una frazione dell’energia prelevata non e’ trasformabile in lavoro.
Questa parte e’ E = To ( Q/Tc)
Si noti che (- Q/Tc) e’ la variazione di entropia del serbatoio a T superiore e
Q/Tc e’ la variazione di S della macchina provocata dall’assorbimento di Q !!!
La frazione inutilizzabile aumenta in presenza di passaggi irreversibili
l’aumento e’
ΔE = To ΔS irr
Non c’e’ nessuna violazione del primo principio : l’energia totale rimane costante,
Solo che una parte non e’ utilizzabile per produrre lavoro
Questa parte e’ tanto piu’ piccola quanto minore e’ la variazione di S nel processo
Di assorbimento del calore e quanto minore e’ la temperatura To dell’ambiente.
12/05/2010
TERMODINAMICA_1
28
Primo principio: esiste una funzione U ,delle variabile di stato del sistema,
Detta energia interna le cui variazioni hanno la forma dU =δQ – δW.
La somma della variazioni di U e di quelle dell’energia dell’ambiente = 0
Secondo principio : esiste una funzione S delle variabili di stato del sistema
Le cui variazioni , definite come dS = dQ/T, sommate a quelle indotte
nell’ambiente non puo’ mai essere minore di zero.
12/05/2010
TERMODINAMICA_1
29