Sistemi di coordinate

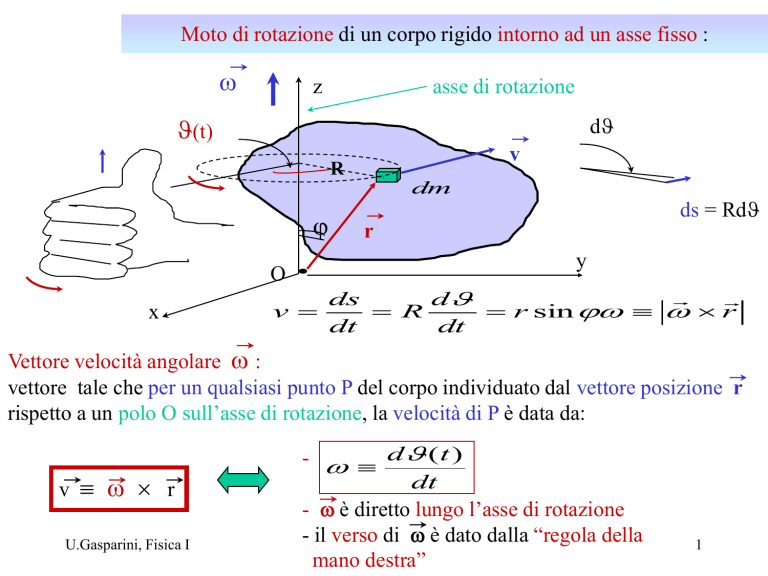
Moto di rotazione di un corpo rigido intorno ad un asse fisso :
w
z
asse di rotazione
J(t)
dJ
v
R
dm
j
r
y
O
x
ds = RdJ
v 


ds
dJ
 R
 r sin jw  w  r
dt
dt
Vettore velocità angolare w :
vettore tale che per un qualsiasi punto P del corpo individuato dal vettore posizione r
rispetto a un polo O sull’asse di rotazione, la velocità di P è data da:
v w  r
U.Gasparini, Fisica I
- w  dJ ( t )
dt
- w è diretto lungo l’asse di rotazione
- il verso di w è dato dalla “regola della
mano destra”
1
Momento angolare per un moto di rotazione intorno ad un asse :
Dato un polo O sull’asse di rotazione z , la componente di LO lungo l’asse z :


 
LOz    r  v dm 
è data da:
LOz  I zw


Corpo
z
“momento di inerzia”
del corpo rispetto all’asse z :
w

Iz 
Corpo
z
j



dLO  r  v dm
dm
dLO  rvdm 
r
dLO
Contributo
O
(infinitesimo) di dm al
momento angolare totale LO
Integrando su tutto il corpo:
LOz   dLOz 
U.Gasparini, Fisica I
distanza dall’asse z
dell’elemento dm
v
R
/2j
R 2 dm
dLOz
R
wRdm
sin j

R2
 dLO cos(
j) 
wdm sin j
2
sin j
dLOz  wR 2 dm
2
2
w
R
dm

w
R
dm


 Iz
2
Momento di inerzia
Iz  
Kg  m2
Dimensioni del momento d’inerzia:
Il momento d’inerzia dipende dalla forma geometrica del corpo, dalla sua
distribuzione di massa (densità) e dall’asse considerato;
non è una proprietà intrinseca del corpo
Esempio:
momento d’inerzia di un asta omogenea di lunghezza

e massa M:
i) rispetto ad un asse perpendicolare passante per un suo estremo :

z
Iz 
R
2
dm 
Corpo
x
dm
R

2
dx 
0
x
 3
3
Iz
densità lineare
M 2

3
ii) rispetto ad un asse perpendicolare passante   M /  / 2
3
2


per il suo centro di massa :
I z  2  x 2 dx 
24
z
/2
0
G
R
dm
x
Iz
M 2

12
Esempi di calcolo di momenti di inerzia
Momento d’inerzia di un disco omogeneo di raggio R e massa M rispetto all’asse
perpendicolare passante per il suo centro di massa :
i)
z
dr
dm 
G
  M / R 2
densità superficiale:

I zG 
r
R
dS   2rdr
R
r 2 dm 
Corpo

r 2 2rdr 
0
2R 4

4
I zG
MR 2

2
ii) Momento d’inerzia di una sfera omogenea di raggio R e massa M :
disco di massa dM(z), momento d’inerzia dI(z)
r ( z)  R 2  z 2
z
dM ( z)  dV  r ( z) 2 dz
dz
z
R
r ( z) 2 dM ( z )
dI ( z ) 
 
2

IG 
 dI ( z )
sfera
R
2

0
1
2
1
2
r ( z) 4 dz 
 ( R
2
 z
 5
2
R5 
8
5
   R 
R 

R 5

3
5 
15



2
)
2
1
2
dz
 M /
4
R 3
3
 ( R 2  z 2 ) 2 dz
 R4  2 R2 z 2  z 4
IG 
2
MR 2
5
Teorema di Huygens-Steiner
Teorema di Huygens-Steiner
(o “degli assi paralleli”) :
I z  I z ' CM  Md 2
momento d’inerzia rispetto
all’asse z’// z e passante per il CM
z
massa totale
del corpo
z’
R
distanza tra z e z’
P = (x,y,z,) = (x’,y’,z’)
R’
dm
y,
G
x
Iz 



x  x'
x’

( x 2  y 2 ) dm 
Corpo
[ x ' 2  ( y ' d ) 2 ]dm 
Corpo

 R'
y  y ' d
d
R 2 dm 
Corpo

[ x ' 2  y ' 2 2 y ' d  d 2 ]dm
Corpo
2
 y' dm  d
dm  2d
Corpo
U.Gasparini, Fisica I
y’
2
Corpo
I z 'CM
 y ' CM  0
= R’2
 dm  I
z ' CM
 Md 2
Corpo
5
=M
Esempi di applicazione del teorema di Steiner :
i) z
d  /2
G
ii)
I z  I z ' CM  Md 2 
z’
dm
2
M 2
M 2
 

 M 

 2
12
3
(cfr. slide n.3)
Momento d’inerzia di un disco omogeneo di massa M e raggio R rispetto ad un asse
ad esso perpendicolare passante per un punto P sul suo bordo :
z
P
d=R
z’
I z P  I z 'CM  Md 2 
G
2
MR 2
3
MR

 MR 2 
2
2

I zP
3 MR 2

2
Si noti che:
un disco che ruoti senza strisciare (“puro rotolamento”) compie una rotazione intorno all’asse
istantaneo passante per il punto di contatto col piano di appoggio
w
z
G
vG
U.Gasparini, Fisica I
P
6
Teorema del momento angolare per un corpo rigido
Il teorema del momento angolare ( “ 2a equazione cardinale” della dinamica):
massa totale del sistema

 (E)
dLO


 MO
 vO  MvG
dt
momento totale
delle forze esterne
rispetto al polo O
velocità del polo O nel sistema
di riferimento inerziale nel quale i
Punti materiale hanno le velocità v
che entrano nella definizione

 
di LO :
L 
r  vdm
O

Corpo
per un corpo rigido in rotazione intorno ad un
asse fisso z ( vO= 0) :
z
w

 (E)
dLO
 MO
dt
può essere riformulato utilizzando il concetto di momento
d’inerzia. Proiettando tale equazione lungo l’asse di rotazione:
O
dLOz
d ( I zw )
dw
(E)

 Iz
 M Oz
dt
dt
dt
(E)
M Oz
 I z
U.Gasparini, Fisica I
( in formale analogia con la
legge diNewton:

F  ma )
accelerazione
angolare :
dw (t )
 (t )  7
dt
Equazione fondamentale della dinamica delle rotazioni:
L’equazione fondamentale della dinamica delle rotazioni:
(E)
MO
 I z
z
è formalmente analoga alla 2a legge della dinamica per un punto materiale, con le
sostituzini:
forza risultante F  momento delle forze esterne M
accelerazione a  accelerazione angolare 
Esempio :
massa m
 momento d’inerzia Iz rispetto all’asse
porta in rotazione
di rotazione z
intorno ai suoi
z
cardini
dw (t )
 (t ) 
dt
w(t)
MO =
O
OP
OP  F
F
w(t+dt)
P
forza agente sulla
maniglia


U.Gasparini, Fisica I

M Oz
Iz
braccio minore
MO
O
OP F

Iz
F

OP
P
minore
accelerazione
angolare
8
stessa forza
“Pendolo composto”
Applicazione del teorema del momento angolare:
y
moto di un “pendolo composto”
y
piano di
reazione vincolare
(non ha momento rispetto ad O )
F
z
oscillazione
(x,y)
O
O
J
x
OG
mg

z
O



M O  OG  mg
G
h
M
M Oz  hmg sin J (t )
Proiezione della 2a eq.cardinale lungo l’asse z :
M
(E)
Oz
 I z
Per piccole oscillazioni (sin JJ ) :
d J (t )
2
dt 2

d 2J ( t )
dt 2
 mgh sin J ( t )  I z
mgh
J (t )  0
Iz
g

J (t )  0

U.Gasparini, Fisica I
w
2
x
G
mg
d 2J ( t )
dt 2
Introducendo la
“lunghezza ridotta”   I z
del pendolo composto:
mh
Soluzione : moto armonico
J (t )  J0 sin(wt  j )
9
“Assi reciproci” di un pendolo composto:
piano di
oscillazione
(x,y)
y
“assi reciproci”
asse di rotazione
O
z
h
O
G
h’
O’
“asse di oscillazione” :
asse parallelo all’asse di
rotazione, passante per il
punto O’ a distanza  O
(lunghezza ridotta ) dal punto di
sospensione O lungo la retta OG
z’
mg
I periodi di oscillazione intorno agli assi z e z’ (“assi reciproci”) sono uguali. Infatti:
Iz
I G  mh 2
I
I G  mh O  mh 2
O 

 G h
mh
mh
mh
La lunghezza ridotta per le
oscillazioni intorno ad O’ è:
 h  h'
 O'
I z'
I G  mh' 2
mh O  mh 2  mh' 2




mh'
mh'
mh'
h 2  hh'h 2  h' 2
h' (h  h' )


 h  h'
h'
h'
U.Gasparini, Fisica I
w 
 O'   O
g
O
 w'
g
 O'
“Pendolo reversibile” (o “ pendolo di Kater ”) :
O
m1
Masse
mobili
O’
punti di sospensione
(fissi)
m2
m2
O
m1
O
O’
w 
2

T
g
O
w' 
2

T'
g
 O'
le masse m1 ed m2 vengono spostate finchè i periodi di
oscillazione intorno ad O e O’ sono gli stessi; in tale situazione
la distanza OO’, determinabile con elevata precisione (Dl/l 10-3 )
è la lunghezza ridotta del pendolo composto
 si ottengono misure di
U.Gasparini, Fisica I
g  w 2
-6
di analoga precisione :
Dg
 10  6
g
11
Energia cinetica di un corpo rigido in rotazione
Per un copro rigido in rotazione con velocità angolare w intorno ad un asse z :
z
asse di rotazione
w
J(t)
dJ
v
R
dm
ds=RdJ
v 
Ek 

1 2
v dm 
2
corpo

Ek 


1
1
(wR ) 2 dm 
w2
2
2
corpo
R 2 dm
corpo
 Iz
1 2
1
v dm  I zw 2
2
2
corpo
Analogia formale con l’espressione
dell’energia cinetica di un punto materiale:
Ek
1

mv 2
2
m
U.Gasparini, Fisica I

ds
dJ
 R
 wR
dt
dt
v

Ek 


Iz
w
1
I zw 2
2
Teorema di Koenig per l’energia cinetica di un corpo rigido
Il moto generico di un corpo rigido è, in un dato istante, riconducibile ad un moto
roto-traslatorio, sovrapposizione di un moto di traslazione del centro di massa con
velocità vG e di un moto di rotazione con velocità angolare w intorno ad un asse
istantaneo di rotazione passante per il centro di massa:
vG
w
G
In generale, sia il modulo che la direzione di w variano
istante per istante.
Teorema di Koenig per l’energia cinetica di un corpo rigido:
Ek 
Ek 
U.Gasparini, Fisica I

1
Mv G 2 
2

1
v ' 2 dm
2
corpo
1
1

MvG 2 
I Gw 2
2
2
momento d’inerzia rispetto all’asse
istantaneo di rotazione passante per G
13
Energia cinetica di un copro rigido
Il teorema di Koenig per un corpo rigido puo’ essere ricavato dal teorema di
Huygens-Steiner :
w
z
z’
d
vG
vG = wd
G
corpo in rotazione intorno all’asse z
Ek 
1
1
1
1
I zw 2 
( I z '  Md 2 )w 2 
I z 'w 2 
M (dw ) 2
2
2
2
2
vG
t. di Huygens-Steiner
Ek 
U.Gasparini, Fisica I
1
1
I z 'w 2 
MvG 2
2
2
14
Teorema dell’energia cinetica per un corpo rigido:
E)
DE k  E kf  E ki  Wi (
f
Per un corpo rigido,il lavoro infinitesimo dW(I) delle forze interne è nullo:
lavoro delle sole
forze esterne
dm j

r jk
dmk
 (I)
 




dW

Fj
 dr j 
F jk  dr j 

j
j
k j






 F12  dr1  F13  dr1 ... F21  dr2 .... 






 F12  ( dr1  dr2 )  F13  ( dr1  dr3 ) .... 








 F12  d ( r1  r2 )  F13  d ( r1  r3 ) .... 
F jk  dr jk  0
(I)

 
 
j
k j
poichè in un corpo rigido le distanze relative rjk rimangono invariate
U.Gasparini, Fisica I
0
15