“Corpo rigido”
Distribuzione estesa di massa i cui punti mantengono invariate le distanze reciproche
( non ci sono deformazioni)
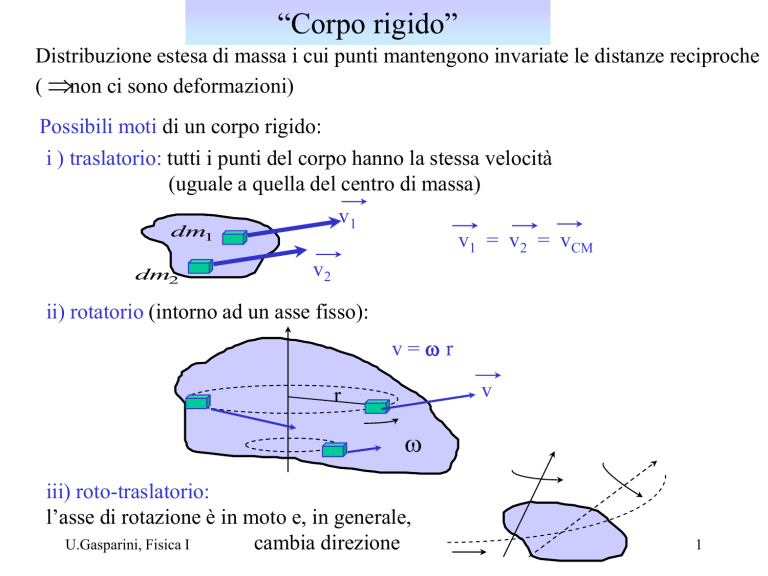
Possibili moti di un corpo rigido:
i ) traslatorio: tutti i punti del corpo hanno la stessa velocità
(uguale a quella del centro di massa)
v1
dm1
dm2
v1 = v2 = vCM
v2
ii) rotatorio (intorno ad un asse fisso):
v=wr
v
r
w
iii) roto-traslatorio:
l’asse di rotazione è in moto e, in generale,
cambia direzione
U.Gasparini, Fisica I
1
“Gradi di libertà” di un sistema
numero n di parametri indipendenti necessari a descriverne
il moto ( definirne completamente la posizione)
Esempi:
- punto materiale in moto nello spazio tridimensionale:
P = ( x(t), y(t), z(t) )
n=3
- sistema di N punti materiali indipendenti:
Pi = ( x i (t) , y i (t), z i (t) )
n=3N
- 2 punti materiali vincolati a mantenere una distanza fissa
P2 = ( x 2 (t) , y 2 (t), z 2 (t) )
n = 5 ( = 3 2 - 1)
d=costante
P1= ( x 1 (t) , y 1 (t), z 1 (t) )
- corpo rigido :
n=6
U.Gasparini, Fisica I
equazione di vincolo:
( x1 x2 ) 2 ( y1 y2 ) 2 ( z1 z2 ) 2 d 2
2
Gradi di libertà di un corpo rigido
I gradi di libertà di un corpo rigido sono 6 :
u1
z
x
u3
sistema di assi solidale rispetto
al corpo rigido
CM
u2
y
posizione del centro di massa :
3 gradi di libertà
orientazione degli assi :
u1 ( u1x , u1 y , u1z )
u2 ( u2 x , u2 y , u2 z )
u3 ( u3 x , u3 y , u3z )
condizioni:
u1 1
u2 1
u3 1
9
u1 u2 0
u1 u3 0
u2 u3 0
parametri
6
equazioni
9 - 6 = 3 parametri indipendenti
U.Gasparini, Fisica I
6 gradi di libertà
3
Esempio: orientazione di un corpo rigido nello spazio
Dati 3 punti arbitrari non allineati del corpo:
2 parametri (J , j)
per definire la direzione
dell’asse 1-2 nello spazio
2
F
J
j
U.Gasparini, Fisica I
1
3
1 parametro ( F ) per definire
la direzione dell’asse 2-3
nel piano ^ all’asse 1-2
4
Densità
La materia, osservata su scala atomica ( 10 -10 m) ha una struttura discontinua .
Volumi “ infinitesimi” su scala macroscopica ( molto piccoli rispetto alle
variazioni delle proprietà macrospiche, come la densità, della materia, e
Comunque rispetto alle dimensioni tipiche dei corpi considerati) contengono un
numero enorme di atomi :
esempio: numero N di atomi in 1 cm3 di rame:
densità:
Cu 8,96g / cm3
NA
NA
6,02 10 23
22
N
8
,
5
10
atomi/cm3
3
Vmole
mmole / Cu
63,55 g / 8,96 gcm
Su volumi (macroscopicamente) infinitesimi la materia puo’ essere considerata una
distribuzione continua di massa.
“Densità media” di un corpo di volume V e massa m :
U.Gasparini, Fisica I
m
V
5
Densità (di volume) di un corpo
Funzione continua dei punti dello spazio occupati dal corpo:
massa contenuta nel volume V
( x , y , z ) lim
V 0
mV
dm
V
dV
volume centrato nel punto (x,y,z)
V
P = (x,y,z)
dimensioni:
[ ] = kg / m 3
Densità superficiale :
( x , y ) lim
S 0
mS
dm
S
dS
[ ] = kg / m2
S
Densità lineare :
( x ) lim
0
U.Gasparini, Fisica I
m
dm
d
[ ] = kg / m
6
Centro di massa di un corpo rigido C
“Centro di massa” G di un sistema di punti materiali Pi :
OG rCM
i
mi OPi
i
P1
z
r1
rCM
mi
P2
i
mri
M
massa totale
del sistema
G
y CM
zCM
O
yCM
x
xCM
1
OG rCM
M
Per un corpo rigido:
C
z CM
y
V
volume del corpo
G
dm (r )dV
1
r dm
M
x CM
y CM
r = (x,y,z)
U.Gasparini, Fisica I
volume dV
1
M
1
M
1
M
x CM
P3
zCM
1
M
1
M
1
M
mx
my
mz
i
i
i
i
i
i
r (r )dV
V
x ( x , y , z )dV
V
y ( x , y , z )dV
V
z ( x , y7, z )dV
V
Centro di massa: esempi:
i) centro di massa di un’asta omogenea di lunghezza :
dm dx
xG
O
densità lineare:
xG
G
1
M
x
dx
V
M /
1
xdm
M
xdx
0
2
M
2
2
xG
2
ii) centro di massa di un “semidisco” omogeneo di raggio R:
y
2
2
( y )
y
R
xG 0
dy =
y
G
yG
M
1
M
R
0
R
area infinitesima dS 2( y )dy
x
R
M
densità superficiale
S
2
R 2 / 2
1
ydm
M
y
2
dy
z
2
2
( R 2 y 2 ) 3/ 2
3M
(per simmetria)
ydS
S
M
y R
y 0
z
1/ 2
M
R
y2
0
R 2 y 2 dy
z 3/ 2
dz
M 3/ 2
2
R3
3M
yG
4R
3
Definizioni:
Sistema di punti materiali
Centro
di massa:
rCM
Corpo rigido
i
mri
M
1
rCM
M
1
r dm
M
V
r ( r ) dV
V
Velocità del CM :
drCM (t )
1
vCM ( t )
dt
M
i
mi vi
Quantità di moto:
P
pi
i
mi vi MvCM
P
i
1
M
V
1
vdm
M
dp
V
Momento angolare:
LO
(ri pi )
i
L' CM rCM MvCM
teorema di Koenig
Energia
cinetica :
vCM
Ek
i
E ' k CM
U.Gasparini, Fisica I
1
mvi2
2
1
2
Mv CM
2
teorema di Koenig
LO
v (r )dV
V
vdm MvCM
V
r dp
V
r vdm
V
L' CM rCM MvCM
Ek
V
E ' k CM
1 2
v dm
2
1
2
Mv CM
2
9
Moto puramente traslatorio di un corpo rigido :
Tutti i punti del corpo hanno la stessa velocità, uguale a quella del centro di massa:
1
vCM
M
V
1
vdm
M
V
v1 = v2 = vCM
dm1
G
v
v (r )dV
M
Quantità di moto :
vCM
P
LO
Momento angolare :
V
v1
v2
dm2
(r )dV v
dp
V
=M
vdm MvCM
V
r vdm L' CM rCM MvCM
V
r v ' dm 0
V
LO
r vdm rCM MvCM
velocità relative al CM : = 0
V
U.Gasparini, Fisica I
Ek
1 2
1
2
v dm E ' k CM
MvCM
2
2
V
1 2
1 2
1
v ' dm 0
2
v dm
MvCM
2
Ek
Energia cinetica :
2
V
2
V
10












