“Centro di massa”
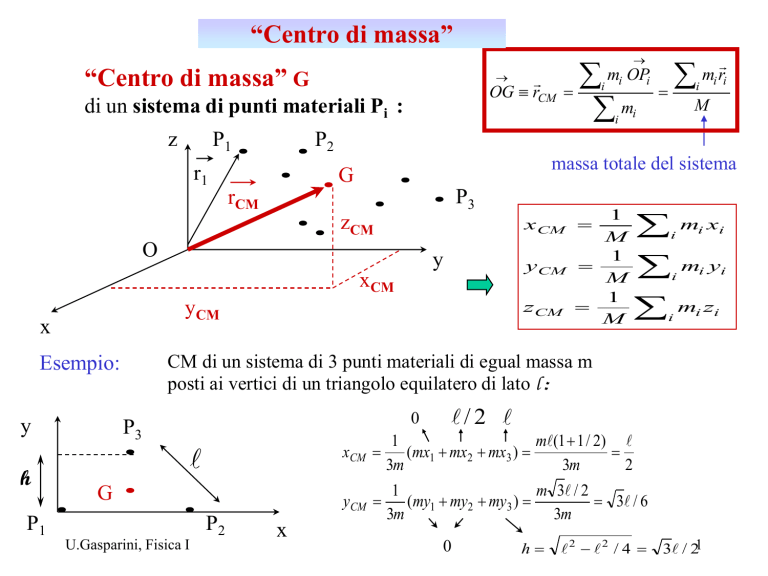
“Centro di massa” G
OG rCM
di un sistema di punti materiali Pi :
P1
z
i
P3
i
M
i
1
M
1
M
1
M
x CM
zCM
O
y
y CM
xCM
yCM
z CM
mx
my
mz
i
i
i
i
i
i
i
i
CM di un sistema di 3 punti materiali di egual massa m
posti ai vertici di un triangolo equilatero di lato l :
Esempio:
h
massa totale del sistema
G
rCM
y
i
mi ri
P2
r1
x
m
mi OPi
0
P3
G
P1
P2
U.Gasparini, Fisica I
x
/2
xCM
1
m(1 1 / 2)
(mx1 mx2 mx3 )
3m
3m
2
yCM
1
m 3 / 2
(my1 my2 my3 )
3 / 6
3m
3m
0
h
2 2 / 4
3 / 21
i
Velocità e accelerazione del CM
drCM (t )
d 1
vCM (t )
dt
dt M
dri (t )
1
mi ri (t )
mi
i
i
M
dt
drCM (t )
1
vCM ( t )
mi vi
i
dt
M
v1
La quantità di moto totale di un sistema
di punti materiali può essere espressa da:
vCM
P
v2
p
i
i
m v
i
i
Mv CM
i
Accelerazione del CM :
dvCM (t )
d 1
aCM (t )
dt
dt M
U.Gasparini, Fisica I
1
mi vi (t )
i
M
dvi (t )
mi
i
dt
dvCM ( t )
1
aCM ( t )
dt
M
i
mi ai
2
Teorema del moto del centro di massa
Per ogni punto materiale Pi di massa m i :
E
I
E
tot
mi ai Fi
Fi
Fi Fi
j i
legge di
Newton
risultante delle forze interne
agenti su Pi
risultante delle forze esterne
al sistema agenti su Pi
CM
P1
Fij
forza interna che
il punto Pj
esercita su Pi
P2
F21 = - F12
F12
Ma CM
E
F1
(es.: m1g )
mi ai
i
RE
Fij
F12 F21 F12 F12 0
E
MaCM R
accelerazione del CM
in un sistema di riferimento inerziale
U.Gasparini, Fisica I
Fi E F12 F13
i
E
Fi
i
i
i
F14 ....... F21 ...
tot
Fi
legge di azione e reazione
risultante delle forze esterne
che agiscono sul sistema
3
Quantità di moto totale del sistema
Esempio:
il CM di un sistema di punti materiali in moto sotto l’azione della forza peso
compie il moto parabolico di un punto materiale soggetto all’accelerazione g :
E
Ma CM R
i
mi g
i
mi
g
aCM g
Considerando la quantità di moto totale del sistema :
P MvCM
E
dP
R
dt
dv CM
dP
M
Ma CM
dt
dt
In particolare, per un sistema isolato o per il quale la forza
risultante di tutte le forze esterne sia nulla :
dP
0
dt
P = costante
la quantità di moto totale si conserva.
U.Gasparini, Fisica I
4
Proprietà del centro di massa
- il momento risultante delle forze peso agenti sul sistema
di punti materiali rispetto ad un polo O é uguale al
momento della forza peso totale applicata nel centro di massa del sistema
tot
MO
mi
Pi
i
ri
O
Mi
G
i
OPi mi g
i
mi OPi g M OG g OG Mg
mi g
tot
M O OG Mg
Mg
- l’energia potenziale della forza peso per un sistema di punti materiali è uguale
all’energia potenziale di un punto materiale di massa uguale alla massa totale
del sistema e coincidente col centro di massa :
Ep
E
p
i
i
U.Gasparini, Fisica I
m gz
i
i
i
g
m z
E p MgzCM
i i
i
MzCM
5
Proprietà dei sistemi di forze parallele
Dato un insieme di forze parallele Fi Fi u
applicate nei punti Pi , esiste un punto C, detto
“centro delle forze parallele”:
OC rC
i
Fi ri
i
Fi
tale che il momento risultante delle forze Fi rispetto ad un
R
generico polo O sia uguale al momento rispetto ad O della risultante
applicata in C. Infatti:
tot
MO
Mi
i
C
Pi
i
O
R
Fi
il centro delle forze peso,
o “baricentro”, è:
rG
U.Gasparini, Fisica I
i
OPi Fi
i
( OPi Fi u )
i
ri
Fi
i
Fi OPi u
Fi OPi
i
Fi
i
Fi u OC R
Se il sistema delle forze parallele è costituito
dalle forze peso:
Fi mi g mi guz
mg
i
mi gri
i
i
m
i
mi ri
i
i
e coincide col centro
di massa.
6
Momento risultante di un sistema di forze
Un sistema di forze Fi applicate in n punti Pi ha un momento risultante che
in generale dipende dal polo considerato:
MO
OPi Fi M O '
i
O' Pi Fi
i
Pi
Fi
OPi
O
Si ha:
O’O
M O'
O' Pi Fi
i
O' O Fi
i
= O’O + OPi
O' O
Fi M O
i
O’
O’Pi
OPi F
i
=MO
risultante del sistema di forze
M O ' O' O R M O
In particolare un sistema di forze a risultante nulla ha un momento che
non dipende dal polo considerato
U.Gasparini, Fisica I
7
Coppia di forze :
Sistema di due forze di egual modulo e direzione e di verso opposto ( R 0 ) .
Il momento di una coppia di forze è indipendente dal polo
rispetto al quale viene calcolato; prendendo come polo il punto A:
M = AB F
J
F
-F
A
B
“braccio”: b= ABsinJ
(= distanza tra le due rette d’azione)
M AB F sin J Fb
Per la legge di azione e reazione, le forze interne di un sistema
costituiscono un insieme di coppie di braccio nullo .
U.Gasparini, Fisica I
8
Momento angolare di un sistema di punti materiali
LO
i
Li
i
ri mi vi
Teorema di Koenig del momento angolare:
LO
rG
i
(
r
r
'
)
m
(
v
v
' )
r
r
m
v
'
'
m
(
v
ri mi vi
i
mi vG
G
i
G
i
MvG
rG Mv G
rG Mv G
Pi
ri =
ri’ +rG
i
i
i
G
i
i
i
i
G
vi ' )
MvG ' 0
r 'm v ' r 'm v
i
i
i
i
i
i
ri ' mi vi '
v i = v i’ + v G
L G’
i
i
i
G
mi ri '
v
G
MrG ' 0
r i’
G
rG
O
i
vG
U.Gasparini, Fisica I
LO rG Mv G
rG Mv G L ' G
r 'm v '
i
i
i
i
9
Teorema di Koenig del mom.angolare: esempi:
Moto traslatorio:
v1
nel sistema di riferimento del CM:
v1’ = v 2’ = 0
r1
G
v2
L' G
vG = v1 = v2
rG
Quantità di moto totale:
Moto roto-traslatorio:
v2’
r2’
i
i
LO rG MvG
O
P MvG
LO rG MvG r1 'm1v1 '
v1’
G
i
i
r2
r1’
r 'm v ' 0
r2 'm2 v2 '
v1
vG
v2
Quantità di moto totale:
rG
O
U.Gasparini, Fisica I
P MvG
10
Teorema del momento angolare
Teorema del momento angolare per un sistema di punti materiali
( “ 2a equazione cardinale” della dinamica):
massa totale del sistema
(E)
dLO
MO
vO MvG
dt
momento totale delle
forze esterne rispetto al polo O
vG
G
ri
vi
Infatti:
=0
vi mi vi vO
U.Gasparini, Fisica I
vO
sistema inerziale
O
i
i
i
dLO
d
ri mi vi
dt
dt
dri
dvi
mi vi
ri mi
dt
dt
O
C
velocità del polo O
nel sistema di riferimento
inerziale nel quale i punti
materiale hanno le velocità vi
che entrano nella definizione
di LO : L
r mv
mi vi
vi vO mi ai Fi
(I)
(E)
F
F
i
i
ri ( Fi ( I ) Fi ( E ) )
MvG
11
Teorema del momento angolare (II)
dLO
vO MvG
dt
(E)
ri Fi
(I)
ri Fi
(E)
(E)
M Oi
MO
=0
Infatti, il momento risultante delle forze interne è nullo:
ri Fi ( I )
i
ri
j i
Fij r1 F12 r1 F13 ...
... r2 F21 r2 F23 .... ( r1 r2 ) F12 ....
F12
=0
poichè le forze interne costituiscono coppie di forze a braccio nullo :
m1
r1
r1 r2 r21 / / F12
F12
F21 = - F12
r12
m2
(r1 r2 ) F12 0
r2
O
Pertanto:
U.Gasparini, Fisica I
(E)
dLO
vO MvG M O
dt
12
Momento angolare (III)
Se il polo O è fisso nel sistema inerziale nel quale sono misurate le
velocità vi dei punti materiali:
(E)
dLO
vO 0
MO
dt
Se il sistema é isolato o il momento risultante delle forze esterne
agenti sul sistema è nullo :
dL
O
dt
0
LO = costante
Il momento angolare totale di un sistema isolato si conserva
Una galassia è con
ottima approssimazione
un esempio di sistema
con momento angolare
costante
U.Gasparini, Fisica I
13
La Supernova della nebulosa del Granchio
Il collasso gravitazionale (e la successiva esplosione) di una “supernova” avviene
conservando il momento angolare della stella originaria.
Al centro dei resti della Supernova della nebulosa del Granchio (esplosione
osservata da astronomi cinesi nel 1054) vi è una “pulsar” (oggetto compatto che
emette un fascio di radiazione e.m. ruotando con un periodo Tpulsar= 33 ms )
Dalla conservazione del momento
angolare [per un oggetto sferico rotante, come
la stella iniziale prima dell’esplosione o la
“pulsar” finale: L= I, dove I=5MR2/2
(vedi più avanti, lezioni sul corpo rigido),
dove M=massa dell’oggetto e R è il suo raggio ]
si ha allora:
L = costante
“pulsar”
I stella stella I pulsar pulsar
2
MRstella
2
MR pulsar
R pulsar Rstella
Assumendo, come
ordine di grandezza: Rstella RSole 106 km
Tstella TSole 25giorni
U.Gasparini, Fisica I
stella
Rstella
pulsar
Tpulsar
Tstella
R pulsar 10 5 RSole 10km
La pulsar è una “stella di neutroni”
(distanze internucleari 1 fm)
14
Momento angolare rispetto al centro di massa
Se viene scelto come polo il centro di massa del sistema:
OG ,
vO vG
(E)
dLG
MG
dt
vG MvG 0
LG
dove:
i
ri mi vi
velocità dei punti materiali
nel sistema inerziale:
vettori posizione
rispetto al polo G
vi v 'i
Applicando il teorema di Koenig del momento angolare:
velocità
rispetto a G
LO rG MvG L' G
i
ri mi vi
al caso in cui O=G :
e quindi:
rG 0
vettore posizione
di G rispetto ad O
(E)
dL' G
MG
dt
r ' m v'
i
i
i
i
LG L' G
L' G
r ' mi vi '
dove
i i
è il momento angolare relativo al sistema del CM,
ossia calcolato utilizzando sia le posizioni ri’ che le velocità vi’ rispetto al centro di massa G.
U.Gasparini, Fisica I
15
i
Energia cinetica di un sistema di punti materiali:
Ek
i
Eik
i
1
mi vi2
2
Teorema di Koenig per l’energia cinetica:
1
mi ( v G vi ' ) 2
i 2
1
1
mi v G 2
mi vi ' 2
i 2
i 2
1
1
Mv G 2
mi vi ' 2 v G
i 2
2
Ek
energia cinetica
associata al moto del CM
Pi
ri =
ri’ +rG
v i = v i’ + v G
ri ’
G
rG
O
U.Gasparini, Fisica I
i
mi vi '
MvG ' 0
energia cinetica EK’
associata al moto
relativo al CM
1 2
1 2
MvG
mv '
i2 i i
2
1
MvG 2 E k '
2
Ek
vG
i
mi v G vi '
16
Teorema dell’energia cinetica
Teorema dell’energia cinetica per un sistema di punti materiali :
I)
(E)
E k E kf E ki Wi (
f Wi f
Fj
lavoro delle forze interne
tra gli istanti iniziale e finale
dsj
lavoro delle
forze esterne
al sistema
Il lavoro infinitesimo dW di tutte le forze
agenti sul sistema quando ciascun punto
materiale
( I ) si sposta
( E ) del vettore infinitesimo dsj è:
Fj Fj
dW
j
Fj ds j
dv j
j
mj
j
d Ek
j
dt
ds j
j
d
Integrando su spostamenti finiti:
j
j
m j a j ds j
m j dv j v j
j
1
d
mv 2
j
j
2
dE
Ek
j
k
posizione finale di
ciascun punto Pj
f
Wi f
dW
f
j
i
dE
j
i
F j ds j
i
f
U.Gasparini, Fisica I
m j aTj ds j
k
j
j
E
k
j
posizione iniz.
E k
Lavoro delle forze interne ed esterne
Nel calcolo del lavoro, si deve tener conto sia delle forze interne che di quelle interne;
il lavoro delle forze interne non è, in generale, nullo :
(I)
Fj
dr j
F jk dr j
j
j
k j
dr1 F13 dr1 ... F21 dr2 ....
(I)
dW
F12
F12
F12 (dr1 dr2 ) F13 (dr1 dr3 ) ....
F12 ( dr1 dr2 ) F13 ( dr1 dr3 ) ....
F12 d ( r1 r2 ) F13 d ( r1 r3 ) ....
r12
r1 ( t )
F12
dr1
k j
0
F12 dr12 0
dr2
1
j
F jk dr jk 0
r2 (t )
O
r12 (t dt )
r12 (t )
r1 (t ) r2 (t )
tempo t
U.Gasparini, Fisica I
2
2
dr12 dr1 dr2
1
tempo t +dt
F12
18










