Lez 2013 11 - La predizione - e-Learning

LA PREDIZIONE O REGRESSIONE
1
DEFINIZIONE DI PREDIZIONE (1)
Si usa una misurazione per predire un’altra
misurazione di comportamento.
 Le misurazioni sono generalmente dei test mentali
(abilità, profitto, personalità, atteggiamenti,
temperamenti) o dati fisici o altre rilevazioni
comportamentali.

2
Concetto della predizione
statistica (regressione):
Se a punteggi alti di un test
(predittore) corrispondono punteggi
alti di un altro test (comportamento
predetto o stimato) e, viceversa, a
punteggi bassi del predittore
corrispondono punteggi bassi del
predetto, si può usare il primo per
predire il secondo.
Si ricorre al concetto matematico di
funzione
Una funzione matematica lega un insieme di
numeri, usando costanti e variabili (e anche altre
funzioni matematiche).
 Es y= k+x
 Y= log 10 (x)
 Y= a+mx


Si deve tenere conto che le predizioni non sono
precise, e quindi la funzione dovrebbe essere
scritta sempre così



Y= mx + a + e
dove e indica la parte di errore della predizione.
Studieremo solo la relazione lineare
DEFINIZIONE DI PREDIZIONE (2)
Dovremo trasformare il punteggio del test predittore
con una equazione di una retta, che predica al meglio
(ovvero commettendo meno errori possibili) il
punteggio ottenuto dal soggetto nel test predetto.
 L’equazione per trasformare il punteggio è la seguente:

yˆi  xi  m  a
6
EQUAZIONE DI REGRESSIONE
yˆi  xi  m  a
La costante additiva a è chiamata intercetta.
Rappresenta il punto in cui la retta incontra
l’asse delle ordinate.
 La costante moltiplicativa m è chiamata
pendenza o coefficiente angolare. Rappresenta il
cambiamento in y all’aumentare di una unità in
x.

7
ESEMPI DI PREDIZIONE
Un test di abilità verbale predice la media dei
voti a scuola.
 Una scala di Stima di sé è usata per predire il
Senso di benessere e di salute psicofisica
 Il punteggio di Coscienziosità predice il livello di
efficienza nel lavoro di gruppo.

8
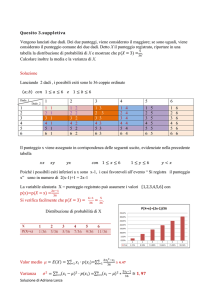
Piccolo esempio numerico
Raccogliamo un piccolo numero di osservazioni:
 Abilità verbale (un test psicometrico)
 Profitto scolastico (voto scolastico dato da
insegnanti)
 Supponiamo che entrambe le misurazioni siano
delle scale a intervalli

Osservazioni per otto studenti
Voto
A
Test abilità verbale
12
B
C
10
14
7
8
D
E
F
G
9
9
13
11
5
6
9
7
H
8
5
scolastico
8
Riportiamo in un grafico cartesiano le
otto coppie di osservazioni
In ascissa indichiamo la variabile indipendente
(Abilità verbale)
 In ordinata riportiamo il valore della variabile
dipendente (Voto scolastico)
 Osserviamo la distribuzione dei punteggi

La disposizione dei
punti indica che c’è una
relazione POSITIVA fra
le due variabili
La relazione POSITIVA
fra le due variabili può
essere descritta e
riassunta con una
RETTA
Quale retta?
Rossa verde o
azzurra?
Quella che è più
vicina a tutti i
punti è la
migliore
Come stabilire i parametri della
retta di predizione?
Che criterio si può seguire?
 Stabilendo
il criterio dei minimi quadrati:
gli errori (ovvero gli scarti tra la retta di
predizione e il punteggio realmente ottenuto
dal soggetto) devono essere il più possibile
piccoli, e il criterio operativo è quello di
considerare il quadrato degli scarti, o errori.
 I metodi dell’analisi matematica forniscono la
risposta con un’equazione dei minimi quadrati.
17
Gli errori positivi devono compensare quelli negativi
 La loro somma è uguale a zero
 Perciò, il criterio da minimizzare non può essere
l’errore semplice, ma


l’errore elevato al quadrato
e la predizione si chiama

Equazione della retta dei minimi quadrati
Errore di previsione negativo
Errore di previsione positivo
Quella che è più
vicina a tutti i punti,
seguendo il criterio
dei MINIMI
QUADRATI
Variabile
dipendente,
spiegata, valore
osservato
Yi  mX i  a   i
inclinazione
Stima di y, valore
predetto
intercetta
variabile
indipendente
errore
Yˆi  mX i  a
Il criterio può essere espresso con la
formula
N
N
2
ˆ
    (Yi  Yi )  min
i 1
2
i
i 1
Formula di calcolo
mr
sy
sx

 ( X  X )(Y  Y )  N  XY   X  Y
N  X  ( X )
(X  X )
i
i
2
i
a  Y  bX
2
2
Applicazione della formule
8 * 611  86 * 55
m

2
8 * 956  (86)
4888  4730 158

 0,626
7648  7396 252
a  6,875  0,626 *10,75  0,135
Yˆ  0,135  0,626 * X
somma
media
abilità
8
9
9
10
11
12
13
14
86
10,75
voto
5
5
6
7
7
8
9
8
55
6,875
voto_pre
detto
5,15
5,78
5,78
6,4
7,03
7,66
8,29
8,91
55
6,875
Predizione
usando i punti
standardizzati
PREDIZIONE CON PUNTI ZETA
zˆ yi  z xi  rxy
ẑyi = zeta predetto
zxi = zeta predittore
rxy = coefficiente di correlazione
27
Test R
Test T
p1
37
p2
Test R
zeta
test T
zeta
50
1,33
0,45
39
75
1,49
1,58
p3
9
24
-0,86
-0,72
p4
8
11
-0,94
-1,31
p5
6
25
-1,09
-0,68
p6
39
78
1,49
1,71
p7
18
24
-0,16
-0,72
p8
16
20
-0,31
-0,90
p9
8
40
-0,94
0,00
p10
20
53
0,00
0,59
somma
200
400
0,00
0,00
dev stan
12,79
22,17
1,00
1,00
varianza
163,60
491,60
1,00
1,00
20
40
0,00
0,00
soggetti
media
PREDIZIONE DEL
PUNTEGGIO
OTTENUTO AL TEST
T TRAMITE IL
PUNTEGGIO AL
TEST R CON I PUNTI
Z.
PRIMO
PASSAGGIO:
TRASFORMAZION
E DEI PUNTEGGI
IN PUNTI Z.
28
Sogg.
Test R zeta
Test T zeta
prediz di
T
p1
1,33
0,45
1,13
p2
1,49
1,58
1,26
p3
-0,86
-0,72
-0,73
p4
-0,94
-1,31
-0,79
p5
-1,09
-0,68
-0,93
p6
1,49
1,71
1,26
p7
-0,16
-0,72
-0,13
p8
-0,31
-0,90
-0,26
p9
-0,94
0,00
-0,79
p10
0,00
0,59
0,00
somma
0,00
0,00
0,000
dev stan
1,00
1,00
0,847
varianza
1,00
1,00
0,718
media
0,00
0,00
0,000
PREDIZIONE DEL
PUNTEGGIO OTTENUTO AL
TEST T TRAMITE IL
PUNTEGGIO AL TEST R CON I
PUNTI Z.
SECONDO PASSAGGIO:
CALCOLO DELLA
PREDIZIONE DI T CON LA
FORMULA:
zˆ yi  z xi  rxy
29
VARIANZA SPIEGATA
SOGGETTO
TEST R
ZETA
TEST T PRODOTTI PREDIZIONE
ZETA
ZETA
DI T
P1
P2
P3
1,33
1,49
0,45
1,58
0,6
2,34
1,13
1,26
-0,86
-0,72
0,62
-0,73
P4
-0,94
-1,31
1,23
-0,79
P5
-1,09
-0,68
0,74
-0,93
P6
1,49
1,71
2,55
1,26
P7
-0,16
-0,72
0,11
-0,13
P8
-0,31
-0,9
0,28
-0,26
P9
-0,94
0
0
-0,79
P10
0
0,59
0
0
SOMMA
0
0
8,473
0
DEVIAZIONE STD
1
1
0,877
0,847
VARIANZA
1
1
0,769
0,718
MEDIA
0
0
0,847
0
Correlazione
Varianza
spiegata
30
VARIANZA SPIEGATA E RESIDUA
SOGGETTO
TEST R
ZETA
TEST T PRODOTTI PREDIZIONE
ZETA
ZETA
DI T
P1
P2
P3
1,33
1,49
0,45
1,58
0,6
2,34
1,13
1,26
-0,86
-0,72
0,62
-0,73
P4
-0,94
-1,31
1,23
-0,79
P5
-1,09
-0,68
0,74
-0,93
P6
1,49
1,71
2,55
1,26
P7
-0,16
-0,72
0,11
-0,13
P8
-0,31
-0,9
0,28
-0,26
P9
-0,94
0
0
-0,79
P10
0
0,59
0
0
SOMMA
0
0
8,473
0
DEVIAZIONE STD
1
1
0,877
0,847
VARIANZA
1
1
0,769
0,718
MEDIA
0
0
0,847
0
La varianza
spiegata è la
varianza dei
predetti, cioè
la varianza
spiegata
dalla
regressione.
31
VARIANZA SPIEGATA E RESIDUA
SOGGETTO
TEST R
ZETA
TEST T PRODOTTI PREDIZIONE
ZETA
ZETA
DI T
P1
P2
P3
1,33
1,49
0,45
1,58
0,6
2,34
1,13
1,26
-0,86
-0,72
0,62
-0,73
P4
-0,94
-1,31
1,23
-0,79
P5
-1,09
-0,68
0,74
-0,93
P6
1,49
1,71
2,55
1,26
P7
-0,16
-0,72
0,11
-0,13
P8
-0,31
-0,9
0,28
-0,26
P9
-0,94
0
0
-0,79
P10
0
0,59
0
0
SOMMA
0
0
8,473
0
DEVIAZIONE STD
1
1
0,877
0,847
VARIANZA
1
1
0,769
0,718
MEDIA
0
0
0,847
0
Correlazione
32
Notiamo che…

La varianza spiegata è la varianza dei predetti,
cioè la varianza spiegata dalla regressione.
33
PROPRIETÀ DELLA REGRESSIONE
 La
varianza dei predetti è uguale al
coefficiente di determinazione: r2
 La deviazione standard dei predetti è uguale
al coefficiente di correlazione (in quanto radice
quadrata della varianza)
34
Per passare dai punti zeta ai
punti grezzi

Si può costruire o calcolare l’equazione di regressione
usando i punti grezzi, senza passare per i punti
standardizzati:
yˆi  zˆyi  sy  My
Ottengo questa formula applicando la formula per
passare dai punti zeta al punteggio grezzo:
x=z·s+m
dove: s = dev. std.
m = media
35
PREDIZIONE CON MISURE
SINTETICHE DI X E Y
sy
sy


yˆi   xi   My - rxy   Mx 
sx
sx


36
ESEMPIO DI PREDIZIONE CON PUNTI GREZZI
SOGGETTI
TEST R
TEST T
P1
P2
P3
P4
P5
P6
P7
P8
P9
P10
37
39
9
8
6
39
18
16
8
20
200
12,79
163,60
20,00
50
75
24
11
25
78
24
20
40
53
400
22,17
491,60
40,00
SOMMA
DEVIAZIONE STD
VARIANZA
MEDIA
COEFF
ANGOLARE (m)
1,469
INTERCETTA (a)
10,632
0,847
CORRELAZIONE
PRODOTTI
R·T
R2
T2
STIME
1850
2925
216
88
150
3042
432
320
320
1060
10403
1369
1521
81
64
36
1521
324
256
64
400
5636
2500
5625
576
121
625
6084
576
400
1600
2809
20916
64,97
67,91
23,84
22,37
19,44
67,91
37,06
34,12
22,37
40,00
400
18,79
352,96
40,00
37
RIASSUMENDO DALLA TABELLA
Il soggetto p1 ha avuto punteggio 37 nel test R e 50 nel
test T.
 Il test R è usato per predire il test T.
 Per predire il punteggio di p1 si utilizza l’equazione di
regressione:

T=R·m+a
se m = 1.469 e a = 10.623
T= 37 ·1.469 +10.623= 64.97
38
Ricordiamo la correlazione
fra le due misurazioni
Correlazioni
ab_verbale
ab_verbale
Voto_
scolastico
Correlazione
1
,912**
di Pearson
Sig. (2-code)
,002
N
8
8
Voto_scolastico Correlazione
,912**
1
di Pearson
Sig. (2-code)
,002
N
8
8
**. La correlazione è significativa al livello 0,01 (2-code).
Regressione con SPSS...
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Sig.
,918
,002
Costante additiva. E’ il valore della VD
quando la VI è uguale a zero. In psicologia ha
un senso relativo, dovuto all’arbitrarietà delle
unità di misura (per i test mentali)
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
t di Student e sua significatività. Se non
significativo, può essere omesso
nell’equazione di regressione.
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Sig.
,918
,002
Errore standard della distribuzione
campionaria della costante additiva. Serve
per calcolare t e la significatività. In questo
caso è molto grande in rapporto a B. La stima
di B dà un valore non significativo
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
Perché non c’è niente qui?
t
,107
5,460
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
Ecco la costante moltiplicativa: è
il valore che moltiplica il
punteggio dell’abilità verbale
t
,107
5,460
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Cefficiente beta standardizzato: con
una sola VI, è uguale a r.
Indica l’ammontare di cambiamento
della VD per ogni unità della VI.
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
t di Student: se è significativa, si
interpreta come valore diverso da
zero, utile perciò nella predizione della
VD
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Significativià di t: se inferiore a 0,05,
indica significatività del parametro b
nella popolazione.
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Errore standard (=deviazione standard
della distribuzione campionaria del
parametro moltiplicativo nella
popolazione). Serve per calcolare la
significatività
Sig.
,918
,002
Coefficientia
Coefficienti non
standardizzati
Modello
B
Errore std.
1
(Costante)
,135
1,255
ab_verbale
,627
,115
a. Variabile dipendente: Voto_scolastico
Coeffici
enti
standar
dizzati
Beta
,912
t
,107
5,460
Errore standard (=deviazione standard
della distribuzione campionaria del
parametro moltiplicativo nella
popolazione). Serve per calcolare la
significatività
Sig.
,918
,002
Riepilogo del modello
R-quadrato
Modello
R
R-quadrato
corretto
1
,912a
,832
,805
a. Stimatori: (Costante), ab_verbale
Errore std.
della stima
,644
R multiplo: indica la precisione della
predizione. Importante nella regressione
multipla. In quella semplice, R = r.
È un valore sempre positivo, anche quando r
è negativo.
Riepilogo del modello
R-quadrato
Modello
R
R-quadrato
corretto
1
,912a
,832
,805
a. Stimatori: (Costante), ab_verbale
Quadrato di R multiplo. Se moltiplicato
per 100, dà la percentuale di varianza
spiegata dalla VI
Errore std.
della stima
,644
PERCHÉ STIMARE DEI VALORI CHE
ABBIAMO GIÀ IN REALTÀ?

Per testare le capacità del test di predizione, per
poterlo poi usare in situazioni reali, dove non si
conosce il punteggio da predire.
53
PARAMETRI
 Le
rilevazioni eseguite su un
campione forniscono dei riassunti
(variabili casuali) che stimano i
parametri della popolazione.
 I parametri della popolazione
possono essere uguali a zero (e non
influenzano la regressione) o diversi
da zero (e allora la influenzano).
54
PRECISIONE DELLA STIMA


Il punteggio predetto 30 è vicino a quello osservato, o
reale, che non è conosciuto, ma è stimabile: c’è il 90% di
probabilità che il valore esatto o osservato si situi entro
l’intervallo 30-19.03 e 30+19.03, ossia fra 10.97 e 49.03
Il punteggio predetto 90 è vicino a quello osservato, o
reale, che non è conosciuto, ma è stimabile: c’è il 90% di
probabilità che il valore esatto o osservato si situi entro
l’intervallo 90-19.03 e 90+19.03, ossia fra 70.97 e 119.03
55
RIASSUMENDO
 La
regressione statistica permette di
stimare (o predire) il punteggio di un test
(o di un’altra misurazione).
 Nella predizione del singolo caso non è
mai possibile sapere se la predizione è
esatta o molto sballata.
 Si può quantificare la predizione totale,
fatta su tutti i casi (presenti e futuri): la
quota di varianza spiegata (r2) è un utile
indice per definire la precisione della
predizione.
56
MECCANISMO DELLA PREDIZIONE O
DELLA STIMA



Per ogni individuo, l’equazione della regressione
predice un valore di Y, indicato con Ŷ, simile ma
non uguale al valore osservato Y
Y sta vicino a Ŷ, con alta probabilità è molto
vicino, con bassa probabilità è molto lontano dal
valore vero
Perciò, se non si può calcolare il punteggio reale,
si può affermare che esso deve trovarsi con il 90
% (o altri livelli) di probabilità entro un certo
intervallo calcolabile.
57