spazio esiti Si = [TT,TC,CC]

Esempi elementari
con diagrammi ad albero
e determinazione di probabilità
verificabile sperimentalmente
e intuitivamente
(senza formule)
Lancio di due monete in successione (s)
lancio di due monete insieme (i)
può uscite testa T o croce C
Campioni T, C
esiti possibili TT, TC , CT, CC
spazio esiti per una sola moneta S1 = [T,C]
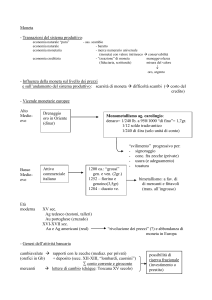
spazio esiti Ss = [TT,TC, CT, CC]
spazio esiti Si = [TT,TC,CC]
Lancio prima moneta
Diagramma ad albero Ss
Lancio seconda moneta
TT
P(TT)=1/4
T
T
TC
P(TC)=1/4
C
T
CT
C
CC
P(CT)=1/4
C
P(CC) = 1/4
Lancio di due monete in successione (s)
lancio di due monete insieme (i)
può uscite testa T o croce C
Campioni T, C
esiti possibili TT, TC , CT, CC
spazio esiti per una sola moneta S1 = [T,C]
spazio esiti Ss = [TT,TC, CT, CC]
spazio esiti Si = [TT,TC,CC]
Lancio prima moneta
Diagramma ad albero Ss
Lancio seconda moneta
TT
P(TT)=1/4
T
T
TC
P(TC o CT)=1/2
C
T
CT
C
CC
P(CT o TC)=1/2
C
P(CC) = 1/4
lancio di due monete insieme (i)
può uscite testa T o croce C
Campioni T, C
esiti possibili TT, TC , CC
spazio esiti per una sola moneta S1 = [T,C]
spazio esiti Si = [TT,TC,CC]
Diagramma ad albero Si
TT
TC
CC
Lancio monete insieme
P(TT)=1/3
P(TC ))=1/3
P(CC) = 1/3
Lancio di tre monete in successione
Spazio campioni per una moneta S1 = (T,C)
TTT
P(nessuna C)
=1/8
TTC
P(almeno 1 C)
= 7/8
TCT
P(almeno 2 C)
TCC
=4/8=1/2
CTT
CTC
P(nessuna T)
=1/8
CCT
CCC
P(almeno 1 T)
= 7/8
Prima moneta
Seconda moneta
Terza moneta
Spazio campioni
S=[TTT.TTC.TCT.TCC.CTT.CTC.CCT.CCC]
Esiti possibili 8
Lancio di tre monete insieme
Spazio campioni per una moneta S1 = (T,C)
TTT
P(nessuna C)
=1/6
TTC
P(almeno 1 C)
= 5/6
TCT
P(almeno 2 C)
TCC
=3/6=1/2
CTC
CCC
P(nessuna T)
=1/6
P(almeno 1 T)
= 5/6
Prima moneta
Seconda moneta
Terza moneta
Spazio campioni S=[TTT.TTC.TCT.TCC.CTC.CCC]
Esiti possibili 6
Urna con 3 palline rosse R1, R2, R3 e 2 azzurre A1, A2
si estrae una pallina , la si rimette nell’urna, si estrae una seconda pallina
Spazio campioni S = [R1, R2, R3, A1, A2]
Eventi = 25
1^ estratta, reinserita
2^ estratta: registrate secondo ordine estrazione
Cfr.prossima
P(nessuna azzurra)=9/25
[R1, R2, R3, A1, A2]
P(solo 1 pallina azzurra)= 12/25
P(con due palline azzurre)=4/25
Eventi = 25
R1
R2
R3
A1
A2
S= [R, V, A]
Urna con palline : 2 rosse, 2 verdi, 2 azzurre
Probabilità uscita prima pallina P1, seconda pallina P2
P1r(2/6 = 1/3
P1v(2/6 = 1/3)
Prima pallina estratta
P1a(2/6 = 1/3)
Seconda pallina estratta
P2r(1/5)
P2a(2/5)
P2v(2/5)
P2r(2(5)
P2a(2/5)
P2v(1/5)
P2r(2/5)
P2a(1/5)
P2v(2/5)
r1
Urna con 3 palline rosse e due azzurre
r2
r3
a1 a2
Si estrae una prima pallina, non si reinserisce;
si estrae una seconda pallina dalle 4 rimanenti
Numero campioni 5*4 = 20
Prima pallina
Seconda pallina
P(nessuna azzurra)=6
P(una azzurra) = 12
P(con 2 azzurre) = 2
Determinare alcune probabilità