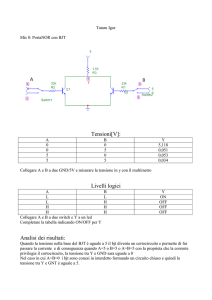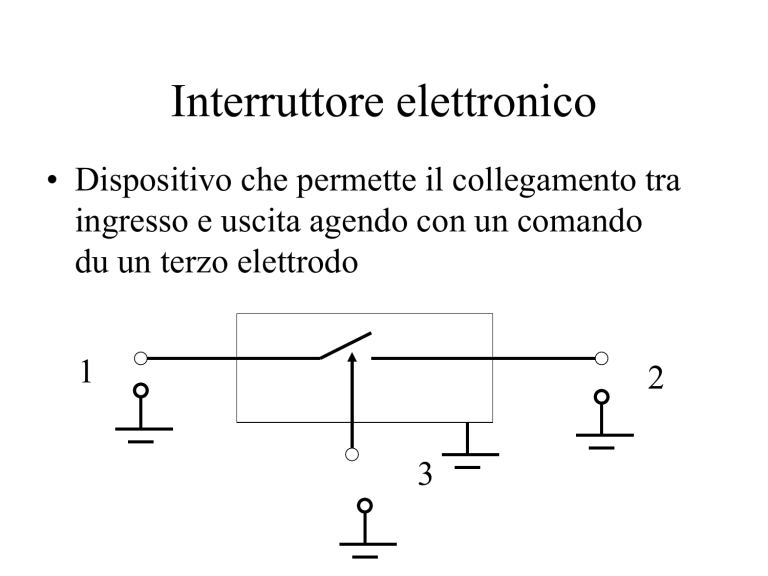
Interruttore elettronico
• Dispositivo che permette il collegamento tra
ingresso e uscita agendo con un comando
du un terzo elettrodo
1
2
3
Interruttore ideale
• Comando di chiusura ON corto circuito
• comando di apertura OFF circuito aperto
• non esiste alcun collegamento tra il
terminale di comando 3 e qello di ingresso 1
né tra il 3 e il 2
Interruttore reale
• Resistenza ON
• resistenza OFF
• impedenze e correnti di perdita tra 1 e 3 e
tra 2 e 3
• impedenze e correnti di perdita tra 1 e terra
e tra 2 e terra tramite l’interruttore
• tensione di offset, correnti di offset
• Le caratteristiche prima viste permettono di
costruire un modello statico
dell’interruttore, ma non sono sufficieenti a
caratterizzarlo.
• Occorre avere informazioni sul
comportamento dinamico, ossia cosa accade
quando passo da OFF a ON e viceversa
Xo / Xi
Caratteristica dinamica
interruttore
1
0.9
0.1
t
td
tr
ts
ON
OFF
td tf
• Xo / Xo rapporto tra la grandezza di uscita
(tensione o corrente) e la corrispondente in
ingresso (tensione o corrente)
• td (on) turn on delay time
• td (off) turn off delay time
• tr rise time
• tf falling time
• ts settling time
Alimentatore stabilizzato
• Passa bruscamente da una condizione di
massima corrente (full load) ad una di
corrente zero (no load)
iout
Full load
no load
t
• Idealmente la tensione di uscita dovrebbe
rimabere costante al valore nominale
Vout
Y
Y
t
x
x
• X è il tempo necessario alla tensione di
uscita per ritornare e mantenersi entro un
intervallo Y della tensione di uscita
nominale
• X è una caratteristica dinamica che prende
il nome di Load transient recovery time
• La caratterizzazione dinamica di un
dispositivo non è compito facile e nei casi
reali il comportamento dinamico di un
sistema dipende non solo dal sistema stesso
ma anche dal tipo di eccitazione adoperato
• nel caso dell’interruttore si è usato uno step
• nel caso dell’alimentatore un impulso reale
di corrente
• Se il sistema è lineare si può usare una
quakunque forma di eccitazione e applicare
il metodo della trasformata di Laplace o
altro metodo matematico per individuare le
caratteristiche del sistema
• se il sistema non è lineare non esiste un
metodo matematico generale
• Un ulteriore problema nasce dal fatto che il
comportamento transitorio di uno strumento
può essere determinato da una grandezza di
influenza e quindi da una porta di ingresso
che non è quella della grandezza da
misurare
• Quando si vuole considerare il
comportamento dinamico di uno strumento
occorre decidere le porte di ingresso a cui
applicare il segnale forzante e il tipo di
segnale forzante
Funzioni forzanti
•
•
•
•
Gradino
impulso reale
rampa
sinusoide che parte da un istante fissato
• Nel caso di sistemi lineari qualunque
funzione forzante è equivalente alle altre,
anche se mette meglio in risalto un aspetto
della risposta
• nel caso reale invece ognuna è più adatta
secondo il tipo di situazione che il sistema
deve affrontare
• se il caso reale non è caratterizzato dalle
funzioni sopra indicate occorre individuarne
una più adatta
Funzioni forzanti
• Gradino simula la situazione in cui in un
sistema reale viene applicata una variazione
improvvisa Tale funzione è adatta per
sistemi che rispondono rapidamente, quali
quelli elettronici e ottici
• rampa è più indicata nel caso di sistemi che
rispondono lentamente, quali quelli
meccanici e termici
• Impulso reale in un sistema lineare ha un
transitorio simile a quello del gradino. La
differenza sta nel fatto che la sollecitazione
brusca è ripetuta in senso opposto dopo un
intervallo di tempo più o meno breve
rispetto alle costanti di tempo del sistema
• La funzione sinusoidale, che inizia in un
dato istante, eccita inizialmente il
transitorio, che poi decade lasciando il posto
alla risposta permanente, anch’essa
sinusoidale se il sistema è lineare
• La risposta permanente viene in genere
caratterizzata tramite la funzione
sinusoidale vobulata (spazzata in frequenza)
ottenedo i diagrammi di Bode
Caso dei sistemi lineari