Gli acceleratori di particelle
C. Biscari
Divisione Acceleratori
LNF-INFN
16 - 18 Settembre 2002
Perche’gli acceleratori ?
I primi acceleratori di particelle furono realizzati per studiare i
costituenti più piccoli della materia.
Un fascio di particelle (elettroni, positroni, protoni,…) che colpisce
una targhetta o collide con un altro fascio produce reazioni
nucleari, annichilazioni e creazione di nuove particelle
Lo studio di questi fenomeni ci dà informazioni sui costituenti
ultimi del nostro mondo
I primi fasci di particelle per gli studi di
fisica nucleare e subnucleare erano
sorgenti naturali: particelle alfa, raggi
cosmici
La capacità di rompere le barriere
elettrostatiche intorno ai nuclei
aumenta con l’energia: l’energia
massima delle particelle alfa è solo 10
MeV.
I raggi cosmici, anche quando molto
energetici, non sono prevedibili:
servono fasci di particelle ad alta
energia e ripetibilità per studi
sistematici.
I primi studi sugli acceleratori sono
degli anni 20
I primi acceleratori sono degli anni 30
Evoluzione degli acceleratori
La capacità di rompere le barriere elettrostatiche intorno ai nuclei
aumenta con l’energia
La capacità di creare nuove particelle
aumenta con l’energia e la corrente
Lo sviluppo degli acceleratori è stato determinato dalla necessità di
ottenere energie e intensità di fasci sempre maggiori
Diagramma dell’energia degli acceleratori dal 1930 al 2010
Un ordine di grandezza
ogni 7 anni
per un totale di 13
(Livingston Chart)
Acceleratori nel mondo
CATEGORIA
NUMERO
Impiantazioni ioniche
Adroterapia
7000
1500
1000
5000
200
20
Sorgenti di luce di sincrotrone
70
Ricerca nucleare e subnucleare
110
TOTALE
15000
Acceleratori nell’industria
Acceleratori in ricerca non-nucleare
Radioterapia
Produzione di isotopi per medicina
Gli acceleratori
usati per la
ricerca pura
sono costruiti ai
limiti della
tecnologia
attuale e sono
anch’essi
ricerca
tecnologica.
L’albero del tempo delle applicazioni degli acceleratori
Sorgenti di particelle
Tutti i fasci di particelle hanno origine in una sorgente
L’esempio più semplice è un
filamento caldo, come quello
di una lampadina
DE = qV
Gli elettroni sono estratti dal
catodo e viaggiando verso
l’anodo positivo acquistano
un’energia uguale alla loro
carica moltiplicata per la
differenza di potenziale
applicata tra catodo e anodo
I protoni sono il nucleo
dell’atomo di idrogeno.
Applicando la differenza di
potenziale al gas di idrogeno
si accelerano i protoni
Primi acceleratori nella storia
1925-1935
Acceleratori elettrostatici –
van der Graff –
Emax 10 MeV
Acceleratori lineari –
Wideroe
Acceleratori circolari –
Ciclotrone 1930,
Betatrone 1940 ,
Sincrotrone 1945
Acceleratori lineari
Le particelle emesse dal filamento vengono
accelerate dal campo elettrico longitudinale
generato da elettrodi susseguenti.
L’idea di Ising (1924) fu applicata da Videroe e
nel 1927 venne realizzato il primo
“drift tube Linac”.
Accelerazione con campi a radiofrequenza:
principio di stabilità di fase
Videroe (1928): applicare, al posto di un campo elettrico statico, un campo
oscillante con frequenza opportuna tale che la fase cambi di p durante il tempo di
volo fra due gap successive.
Se il campo accelerante è una sinusoide e le particelle passano sulla parte crescente
dell’onda, la particella che arriva in anticipo di fase rispetto alla fase sincrona
verrà accelerata di meno, quella in ritardo vedrà un campo maggiore. Le particelle
oscilleranno quindi attorno alla fase corretta raggruppandosi longitudinalmente
Il LINAC di DAFNE a Frascati
Linacs…
Lunghi da pochi m a qualche Km
Energie da pochi MeV a diversi GeV
berkeley
Accelerazione = aumento di energia
b = v/c
La variazione di velocità
è trascurabile al di sopra
di una certa energia
Velocità delle particelle normalizzata alla velocità della
luce in funzione dell’energia
Gli acceleratori circolari
E.O.Lawrence (1930) ebbe la
brillante idea di curvare le
particelle su una traiettoria
circolare, facendole ripassare molte
volte nello stesso sistema di
elettrodi. Negli acceleratori circolari
il campo magnetico B è diretto
verticalmente; se una particella
relativistica di momento p viaggia
nel campo magnetico
perpendicolare la variazione di
momento è
dp/dt=e v x B
il raggio di curvatura della
traiettoria dipende dalla carica e
dall’energia della particella
L’elettro-sincrotrone di Frascati
1959-1975
L’osservazione su “targhetta”
sincrotrone
bersaglio
S
L
p+/-
LINAC
e-,e+,p …
rivelatori
p, n, etc
La materia è vuota : cio’ che non ha interagito viene perduto
Energia a disposizione dell’interazione dovuta solo al fascio
Il bersaglio è complesso: molte delle particelle prodotte disturbano
l’esperimento
Produzione di antimateria
Sciame elettromagnetico
e-
L’elettrone di
alta energia
penetra nella
targhetta
Produzione di antimateria
Sciame elettromagnetico
la massa si
converte in energia
(fotoni)
e
Produzione di antimateria
Sciame elettromagnetico
il fotone si converte
in un elettrone (e-)
e un positrone (e+)
e+
ee
e+
Produzione di antimateria
Sciame elettromagnetico
e+
e+
e+
+ee
e-
e+
e
e-
e+
e-
e-
e+
e
e+
e-
e+
e-
e+
e-
e+
e-
e
e
e-
e+
questo
processo si
ripete e forma
uno sciame
e+
e-
e+
*Nota: Solo positroni, elettroni, e fotoni sono creati
Produzione di antimateria
Sciame adronico
la particella ad alta
energia penetra nel
mezzo e frattura il
nucleo atomico
della targhetta
producendo
diverse particelle
K+
p
p
n
+
-
-
*Nota: una grande varietá di particelle si può produrre:
per esempio, p, n, , , L, ,
Produzione di antimateria
Sciame adronico
K+
K+
p
K-
n
+
-
e
e
Queste particelle
possono essere
abbastanza
energetiche da
produrre nuove
fratture
Accelerazione dell’antimateria
LINAC per e-
LINAC per e+
Lente focheggiante
Alti campi magnetici
targhetta
Sorgente di positroni di DAFNE
AdA (Anello di Accumulazione)
FRASCATI - 1961-1965
Registrazione dei primi elettroni
accumulati in AdA.
La vita media era 21 sec,
il numero medio 2.3
I COLLIDERS materia-antimateria
ADONE a Frascati 1969-1993
LEP DAFNE
al CERN –diADA
Ginevra
1988-2001
1997
a oggi
a Frascati
1959
LHC al Cern di Ginevra > 2006
Luminosità
• la luminosità L di un
collider è proporzionale
alla capacità di fare
interagire le particelle
Per aumentare la
luminosità si aumenta la
densità dei fasci
Numero di particelle per fascio
e+
e-
N N
L
f collisione
S xS y
Dimensioni trasverse dei fasci:
Si può arrivare a pochi (millesimi di mm)
(Cm -2 sec -1 )
Sezione d’urto
Due particelle che collidono possono produrre tipi diversi di eventi,
alcuni più probabili di altri
la sezione d’urto s di un determinato evento
è proporzionale alla probabilità che l’evento avvenga
Si misura in cm2
Ls = frequenza con cui accadono gli eventi cercati
Si misura in sec-1
Esempio
~1010
~3.000.000 sec-1
e+
e-
N N
L
f collisione
S xS y
2 mm
1032 cm-2 s-1
15 m
F
+
+
+ … ~ 10-29 cm2
frequenza degli eventi Ls=1000 eventi/sec
due fasci di 10 miliardi di particelle ciascuno, che si
incrociano 3 milioni di volte al secondo producono l’evento
desiderato solo una volta ogni 3000 incroci!!!!
DAFNE nei LNF
IL complesso di DAFNE è
formato da tre elementi:
(1) il LINAC;
(2) l’accumulatore;
(3) i due anelli principali.
(4) tre linee di luce di
sincrotrone
Le strutture sono state
completate nel 1997 e le
prime collisioni sono
avvenute nel marzo 1998.
DAFNE
Dafne nel 2002
Equazione basica
per descrivere il movimento di una particella in un acceleratore
dp
q E +v B
dt
E campo elettrico
B campo magnetico
p momento
m massa in var iante
v velocità
q carica
L’unità di misura dell’energia delle particelle è l’elettronvolt [eV]
pari all’energia di una particella di carica unitaria accelerata da
una differenza di potenziale elettrostatico di un volt:
1 eV=1.6x10-19 Joules
Più usati negli acceleratori i multipli [keV, MeV, GeV]
Spazio delle fasi delle particelle
Le particelle di un fascio in un acceleratore non hanno tutte la stessa energia e posizione
L’energia, la posizione e il momento trasverso hanno distribuzioni gaussiane
Il pacchetto di particelle è un
elissoide a 6 dimensioni:
y
Energia - posizione longitudinale
Posizione - momento orizzontale
Posizione - momento verticale
s
distribuzione
x
coordinata
Cavità a radiofrequenza
Le cavità a radiofrequenza danno energia al fascio di particelle ogni
volta che esso passa al loro interno
Campo elettrico
fascio
Nei linac c’è un solo passaggio
Negli anelli milioni di passaggi
v = c = 300.000.000 m/sec
Dafne: 100 m : To = 3.3 x 10-7 sec. In 1 sec 3 milioni di giri
LEP: 30 Km : To = 1 x 10-5 sec. In 1 sec 100.000 giri
L’idea di Touschek:
collisioni materia e antimateria
Frascati
La geniale idea di Bruno Touschek fu quella di utilizzare come
particelle collidenti particelle ed antiparticelle che nella loro
annichilazione avrebbero rilasciato tutta la loro energia per creare
nuove particelle
Anello di
Accumulazione
Rivelatore
t
E = m c2
+
-
e-
e+
e-
+
E = 2met c2
e+
t-
Dove si prende l’antimateria?
L’universo, il nostro mondo sono formati da materia:
elettroni, protoni, neutroni,…
I positroni, predetti nel 1927 da un matematico (Dirac),
misurati qualche anno dopo in un esperimento con raggi cosmici (Andersen),
adesso si producono in laboratorio
Così anche gli antiprotoni, l’antimateria dei protoni, anche se la loro
produzione e manipolazione è più complessa
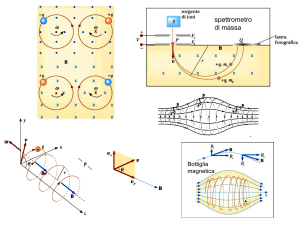
Principali magneti di un anello
DIPOLI – determinano la traiettoria di riferimento
QUADRUPOLI – mantengono le oscillazioni di tutte le particelle
intorno alla traiettoria di riferimento
SESTUPOLI – correggono l’effetto cromatico dei quadrupoli
Radiazione di sincrotrone
Una particella carica che viaggia in una traiettoria curva emette
fotoni, la cui energia dipende dalla massa e dall’energia della
particella e dal raggio di curvatura della traiettoria
Una particella carica che viaggia in una traiettoria curva perde energia.
In un anello di accumulazione l’energia persa viene compensata dalle
Cavità a radiofrequenza
4p ro E 4
U
2 3
3 mc
Energia persa per giro
Emissione di luce di sincrotrone
Campo magnetico
Energia della particella
4p ro E 4
E3B
U
2 3
2 3
3 mc
mc
Massa
E
DE/giro
m
(GeV)
(GeV)
DAFNE
e+ 1
e- 1
0.51
0.51
.000009
.000009
PEP
e+ 14
e- 165
3.1
9.0
.000770
.003570
LEP
e+ 6086
e- 6086
100
100
1.5
1.5
HERA
p 584
e- 579
820
30
.000012
0.13
LHC
p 2800
p 2800
7000
7000
.014
.014
Raggio di curvatura della traiettoria
Il futuro degli acceleratori
Arrivare a energie dell’ordine del TeV: 1012 eV
10 volte di più del LEP
Linear colliders
Arrivare a luminosità 10 volte maggiori delle presenti Factories
Accelerazione di altre particelle ,
Matematica
Elettromagnetismo
Elettronica
FISICA DEGLI ACCELERATORI
Fisica della materia
Informatica
Superconduttività
Tecnica del vuoto
lasers
…
Beauty-Factory: Stanford Linear
Accelerator Center
CLIC
Elettra: Luce di Sincrotrone a Trieste
Bibliografia
• R.Feynman, R.Leighton, M.Sands – “La Fisica di Feynman”
(Vol. 2), Addison Wesley
• R.Wilson, R.Littauer - "Acceleratori di particelle", Zanichelli
• B.Touschek - "Gli anelli di accumulazione", Letture da Le
Scienze Le particelle fondamentali a cura di L.Maiani
• E. Wilson - "An introduction to particle accelerators", Oxford
Divulgativi – adatti ai ragazzi
•http://public.web.cern.ch/Public/ACCELERATORS/Welcome.html
•http://www2.slac.stanford.edu/vvc/accelerators
Livello universitario
•http://www.eece.unm.edu/faculty/humphrie/cpa/cpa.htm