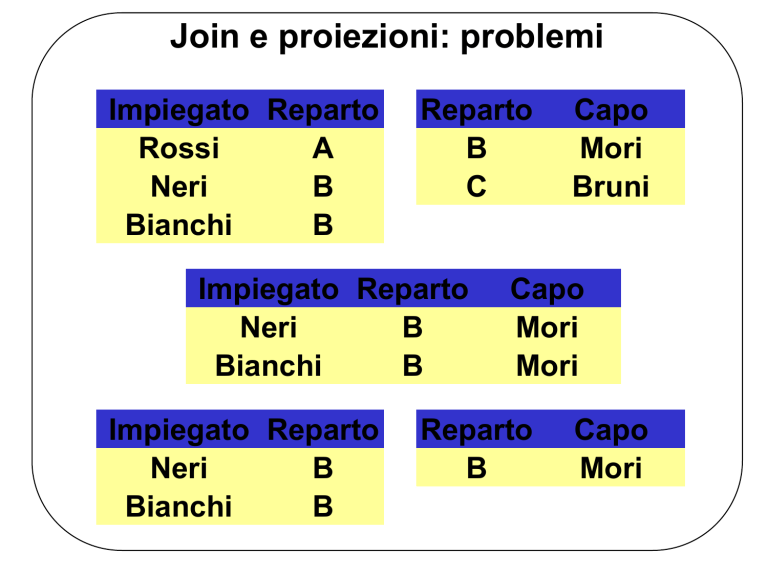
Join e proiezioni: problemi
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
B
C
Impiegato Reparto
Neri
B
Bianchi
B
Impiegato Reparto
Neri
B
Bianchi
B
Capo
Mori
Bruni
Capo
Mori
Mori
Reparto
B
Capo
Mori
Proiezioni e join: problemi
Impiegato Reparto
Capo
Neri
B
Mori
Bianchi
B
Bruni
Verdi
A
Bini
Impiegato Reparto
Reparto
Capo
Neri
B
B
Mori
Bianchi
B
B
Bruni
Verdi
A
A
Bini
Impiegato
Neri
Bianchi
Neri
Bianchi
Verdi
Reparto
B
B
B
B
A
Capo
Mori
Bruni
Bruni
Mori
Bini
Join e proiezioni
• R 1(X1), R 2(X2)
PROJX1 (R 1 JOIN R2 ) R 1
• R(X), X = X1 X2
(PROJX1 (R)) JOIN (PROJX2 (R)) R
Join naturale ed equi-join
Impiegati
Impiegato Reparto
Reparti
Reparto
Capo
Impiegati JOIN Reparti
Impiegati
Impiegato Reparto
Reparti
Codice
Capo
PROJImpiegato,Reparto,Capo ( SELReparto=Codice
( Impiegati JOIN RENCodice Reparto (Reparti) ))
Interrogazioni (Query)
Un’interrogazione è una funzione E(r) che applicata ad
istanze di una base di dati r produce una relazione su
un dato insieme di attributi X.
Le interrogazioni su uno schema di base di dati R in
algebra relazionale sono espressioni i cui atomi (le
variabili) sono relazioni in R.
Esempi
Età Stipendio
Rossi
34
45
Bianchi 37
38
Neri
42
35
Bruni
43
42
Mori
45
50
Lupi
46
60
Impiegati Matricola Nome
7309
5998
9553
5698
4076
8123
Supervisione Impiegato
7309
5998
9553
5698
4076
Capo
5698
5698
4076
4076
8123
• Trovare matricola, nome, età e stipendio degli
impiegati che guadagnano più di 40 milioni
SELStipendio>40(Impiegati)
Matricola Nome Età Stipendio
7309
Rossi
34
45
5998
5698
Bianchi
Bruni
37
43
38
42
9553
4076
Mori
Neri
42
45
35
50
5698
8123
Bruni
Lupi
43
46
42
60
4076
Mori
45
50
8123
Lupi
46
60
• Trovare matricola, nome ed età degli impiegati
che guadagnano più di 40 milioni
PROJMatricola, Nome, Età (SELStipendio>40(Impiegati))
Matricola Nome Età Stipendio
7309
Rossi
34
45
5998
5698
Bianchi
Bruni
37
43
38
42
9553
4076
Mori
Neri
42
45
35
50
5698
8123
Bruni
Lupi
43
46
42
60
4076
Mori
45
50
8123
Lupi
46
60
• Trovare le matricole dei capi degli impiegati che
guadagnano più di 40 milioni
PROJCapo (Supervisione
JOIN Impiegato=Matricola (SELStipendio>40(Impiegati)))
Esercizi
• Trovare nome e stipendio dei capi degli impiegati che
guadagnano più di 40 milioni
• Trovare gli impiegati che guadagnano più del proprio
capo, mostrando matricola, nome e stipendio
dell'impiegato e del capo
• Trovare le matricole dei capi i cui impiegati
guadagnano tutti più di 40 milioni
Equivalenza di espressioni
Due espressioni sono equivalenti se:
E1R E2 se E1(r) = E2(r) per ogni istanza r di R
(equivalenza dipendente dallo schema)
E1 E2 se E1R E2 per ogni schema R
(equivalenza assoluta)
L’equivalenza è importante in quanto consente di scegliere, a parità
di risultato, l’operazione meno costosa.
Equivalenze
• Atomizzazione delle selezioni
F1 F2 (E) F1 (F2 (E))
• Idempotenza delle proiezioni
X (E) X (XY (E))
• Anticipazione della selezione rispetto al join
F (E1 E2) E1 (F (E2) )
Equivalenze
• Anticipazione della proiezione rispetto al join:
X1Y2 (E1 E2) E1 Y2 (E2)
(se gli attributi in X2 - Y2 non sono coinvolti nel join)
Allora:
Y (E1 F E2) Y (Y1 (E1) F Y2 (E2) )
dove Y1 e Y2 sono gli attributi di X1 e X2 compresi in Y o
coinvolti nel join.
• Inglobamento di una selezione in un prodotto
cartesiano a formare un join:
F (E1 E2) E1 F E2
Equivalenze
• Distributività della selezione rispetto all’unione:
F (E1 E2) F (E1) F (E2)
•
Distributività della selezione rispetto alla differenza:
F (E1 - E2) F (E1) - F (E2)
• Distributività della proiezione rispetto all’unione:
X (E1 E2) X (E1) X (E2)
NB La proiezione NON è distributiva rispetto alla differenza
• Tutti gli operatori binari eccetto la differenza godono delle
proprietà associativa e commutativa.
Equivalenze
• Corrispondenze fra operatori insiemistici e selezioni
complesse
F1 F2 (R) F1(R) F2(R)
F1
F2
(R) F1(R) F2(R) F1(R) F2(R)
F1
¬F2
(R) F1(R) - F2(R)
• Proprietà distributiva del join rispetto all’unione:
E (E1 E2) (E E1) (E E2)
Algebra con valori nulli
Estensione degli operatori logici ad una logica a 3 valori
(VERO, FALSO, SCONOSCIUTO (U))
not
and
V U
F
or
V U
F
V
V
F
V
V
V U
F
V
U
U
U U U
F
U V U U
V
F
F
F
F
F F
V
V U
F
Algebra con valori nulli
•A IS NULL è vero su una tupla t se il valore di t su A è
nullo; falso se è specificato.
•A IS NOT NULL è vero su una tupla t se il valore di t su
A è specificato; falso se è nullo.
Età>30 (Persone) restituisce le persone la cui età è nota e > 30 anni
Età>30 Età IS NULL (Persone) restituisce le persone che potrebbero
avere più di 30 anni
Viste (relazioni derivate)
• Rappresentazioni diverse per gli stessi dati (schema
esterno)
• Relazioni di base: contenuto autonomo
• Relazioni derivate:
– relazioni il cui contenuto è funzione del contenuto di
altre relazioni (definito per mezzo di interrogazioni)
Viste
• Relazioni Virtuali (Viste)
Relazioni definite mediante funzioni o espressioni del linguaggio
di interrogazione, non memorizzate ma utilizzabili come se lo
fossero. Devono essere ricalcolate tutte le volte.
• Viste materializzate
Relazioni virtuali effettivamente memorizzate nella base di dati.
Immediatamente disponibili ma critiche per il mantenimento
dell’allineamento con le relazioni da cui derivano. Non sono
supportate dai DBMS.
Viste
Vantaggi
• Permettono di mostrare a un utente le sole componenti della
base di dati che interessano
• Espressioni molto complesse possono essere definite come
viste
• Sicurezza: è possibile definire dei diritti di accesso relativi ad
una vista (e quindi ad una particolare porzione della base di
dati)
• In caso di ristrutturazione della base di dati, le “vecchie”
relazioni possono essere di nuovo ricavate mediante viste,
consentendo l’uso di applicazioni che fanno riferimento al
vecchio schema
Viste, esempio
Afferenza Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Bianchi
• una vista:
Supervisione =
PROJ Impiegato,
Capo
B
Direzione
Reparto
A
B
Capo
Mori
Bruni
B
Bruni
(Afferenza JOIN Direzione)
Interrogazioni sulle viste
• Sono eseguite sostituendo alla vista la sua
definizione:
SELCapo='Leoni' (Supervisione)
viene eseguita come
PROJ Impiegato,
SELCapo='Leoni'(
Capo (Afferenza JOIN Direzione))
Viste, motivazioni
• Schema esterno: ogni utente vede solo
– ciò che gli interessa e nel modo in cui gli interessa, senza essere
distratto dal resto
– ciò che e' autorizzato a vedere (autorizzazioni)
• Strumento di programmazione:
– si può semplificare la scrittura di interrogazioni: espressioni
complesse e sottoespressioni ripetute
• Utilizzo di programmi esistenti su schemi ristrutturati
Invece:
• L'utilizzo di viste non influisce sull'efficienza delle interrogazioni
Viste come strumento di
programmazione
• Trovare gli impiegati che hanno lo stesso capo di Rossi
• Senza vista:
PROJ Impiegato (Afferenza JOIN Direzione) JOIN
REN ImpR,RepR Imp,Reparto (
SEL Impiegato='Rossi' (Afferenza JOIN Direzione))
• Con la vista:
PROJ Impiegato (Supervisione) JOIN
REN ImpR,RepR Imp,Reparto (
SEL Impiegato='Rossi' (Supervisione))
Viste e aggiornamenti, attenzione
Afferenza
Impiegato
Rossi
Neri
Verdi
Supervisione
Reparto
A
B
A
Direzione
Reparto
A
B
B
C
Impiegato
Rossi
Neri
Verdi
Capo
Mori
Bruni
Bruni
Capo
Mori
Bruni
Mori
• Vogliamo inserire, nella vista, il fatto che Lupi ha come
capo Bruni; oppure che Belli ha come capo Falchi; come
facciamo?
Viste e aggiornamenti
• "Aggiornare una vista":
– modificare le relazioni di base in modo che la vista,
"ricalcolata" rispecchi l'aggiornamento
• L'aggiornamento sulle relazioni di base corrispondente a
quello specificato sulla vista deve essere univoco
• In generale però non è univoco!
• Ben pochi aggionamenti sono ammissibili sulle viste