CORSO DI MODELLI
DI SISTEMI BIOLOGICI
Laurea in
Ingegneria Clinica e Biomedica
Modelli di sistemi neuromuscolari
Lo studio della meccanica muscolare può essere condotto secondo due diversi
approcci: un approccio classico in cui il muscolo viene rappresentato con un
modello funzionale basato su un’analogia meccanica e un approccio più moderno
in cui la contrazione muscolare viene rappresentata tenendo conto dei fenomeni
biochimici che si sviluppano nella cellula muscolare durante la contrazione. Tuttavia
il modello classico è tuttora diffusamente utilizzato per la sua semplicità soprattutto
quando il modello del muscolo deve essere inserito in sistemi più complessi o
quando l’interesse riguardi il comportamento globale del muscolo dal punto di vista
dello sviluppo di forza o di una variazione di lunghezza.
Modelli di sistemi neuromuscolari
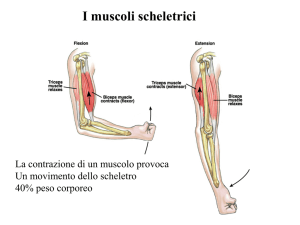
Il muscolo scheletrico.
Il muscolo scheletrico è formato da cellule
lunghe e sottili, dette fibre muscolari. La loro
lunghezza varia da 1 a 50 mm mentre il loro
diametro è solo di 10-100 m. Queste fibre
sono circondate da un rivestimento privo di
struttura chiamato sarcolemma. Le fibre
muscolari,
al
microscopio
elettronico,
presentano un’alternanza di bande chiare e
scure da cui il nome di muscolo striato che
anche viene dato al muscolo scheletrico. Le
bande scure (che hanno una lunghezza media
di 1.5 m) sono dette bande A e presentano al
loro centro una banda chiara detta banda H. Le
bande chiare (di lunghezza 1 m) sono dette
bande I e presentano al loro centro una zona
scura detta Z. Il tratto tra due bande Z
rappresenta l’unità contrattile e si chiama
sarcomero. Quando il muscolo si contrae la
banda I si accorcia mentre la banda A rimane di
lunghezza costante. Le bande Z si avvicinano
durante la contrazione
sarcomero
Z
H
Z
H
I
A
I
A
I
Z
I
Modelli di sistemi neuromuscolari Il muscolo scheletrico.
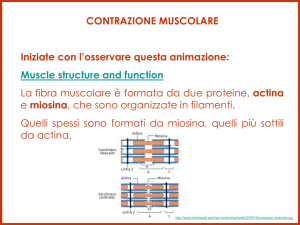
Il muscolo è composto dalle proteine actina (con la tropomiosina e troponina) e miosina. La
miosina è limitata alla banda A mentre i filamenti di actina originano dalla linea Z e terminano
nella zona H. I filamenti di miosina sono filamenti grossi, quelli di actina sottili. I filamenti sottili
sono uniti tra loro a livello delle linee Z. L’accorciamento della fibra muscolare è dovuto
all’azione di ponti trasversali che si formano tra siti preferenziali dei filamenti di actina e
miosina. Questi ponti generano delle forze elastiche che provocano lo scorrimento relativo dei
filamenti l’uno rispetto all’altro. Quando i siti si sono allineati il legame si rompe e un nuovo
ponte si forma con un sito più a valle. Se il muscolo è a riposo la concentrazione di ioni
calcio all’interno della cellula muscolare è bassa e la formazione dei legami è inibita dalla
troponina attraverso la mediazione della tropomiosina. Quando la membrana della cellula
muscolare viene depolarizzata dall’arrivo degli impulsi dal nervomotore ioni calcio penetrano
dall’esterno all’interno della membrana e vengono rilasciati dalle riserve interne alla cellula
contenute nel reticolo sarcoplasmatico. L’eccesso di ioni calcio si lega alla troponina
rimuovendone l’effetto inibitorio. Così l’actina e la miosina si possono legare.
H
miosina
actina
A
L
I/2
Modello classico del muscolo: equazione
di Hill.
L’approccio classico è basato, come già detto su un
modello funzionale “a tre elementi” . Quando il muscolo
non è stimolato, l’elemento contrattile si può
estendere liberamente senza sviluppare forza e le
caratteristiche del muscolo sono rappresentate
dall’elemento elastico in parallelo; quando il muscolo
è stimolato l’elemento contrattile si accorcia con una
velocità che è funzione della lunghezza attuale del
muscolo e del carico. L’elemento elastico serie è stato
introdotto per tener conto del comportamento
osservato quando intervengano brusche variazioni di
carico o di lunghezza. L’equazione costitutiva di tale
modello si ottiene considerando che la lunghezza totale
del muscolo L è uguale alla somma delle lunghezze
dell’elemento contrattile e dell’elemento serie.
L=LCR - +
dove LCR è la lunghezza dell’elemento contrattile a
riposo, è il suo accorciamento ed è la lunghezza
dell’elemento serie. Derivando rispetto al tempo si ottiene:
dL/dt = - d/dt + d/dt
Lcr -
S
T
S
T
T
es
ec
ep
P
P
L
Modello classico del muscolo.
Per quanto riguarda le forze, indicando con T la forza totale esercitata dal muscolo e con P e S le forze
esercitate rispettivamente dall’elemento parallelo e dall’elemento serie, si potrà scrivere:
T=P + S
da cui:
dT/dt = dP/dt + dS/dt
Nell’ipotesi che l’elemento serie e l’elemento parallelo siano puramente elastici, le forze da essi esercitate
dipendono solo dall’allungamento [P=P(L) e S=S(,)], per cui si ottiene:
dT/dt = (dP/dL)(dL/dt) +dS/d· d/dt + dS/d·d/dt
dT/dt = [(dP/dL)+ dS/d](dL/dt) +[dS/d+ dS/d]·d/dt
che è l’equazione base della meccanica muscolare.
Contrazione isometrica (il muscolo si contrae a lunghezza L costante)
dT/dt =+[dS/d+ dS/d]·d/dt
T(0)=Ti
Contrazione isotonica (il muscolo si contrae sotto un carico T=cost )
(dL/dt) = - [dS/d+ dS/d]·d/dt/ [(dP/dL)+ dS/d]
L(0)=Li
La soluzione delle equazioni richiede la definizione delle caratteristiche dell’elemento parallelo, dell’elemento
serie e dell’elemento contrattile, cioè l’espressione delle funzioni P(L), S(,) e d/dt(L,T). In un approccio più
semplificato la S viene considerata funzione della sola . Inoltre si devono anche assegnare l’equazione del
carico in dipendenza della situazione sperimentale considerata o del sistema in cui il muscolo è inserito come
attuatore.
Modello classico del muscolo. Caratteristica dell’elemento parallelo
La caratteristica elastica dell’elemento
parallelo viene rilevata con prove di
allungamento
semplice a
velocità
costante. Al muscolo vengono imposti
degli allungamenti e viene rilevata la forza
elastica sviluppata in corrispondenza ad
ogni allungamento. Naturalmente l’ipotesi
di comportamento puramente elastico in
assenza di stimolazione è valida solo in
prima approssimazione, in quanto anche in
condizioni passive sono stati evidenziati
sperimentalmente effetti di isteresi e di
viscoelasticità. La caratteristica P(L) viene
normalmente rappresentata con l’equazione
10
P [g]
5
P(L) = ·[exp(·(L-Lr))-1]
dove Lr è la lunghezza del muscolo in
condizioni di riposo (P(L)=0 per L<Lr) e
e sono parametri il cui valore può essere
calcolato fittando i dati sperimentali.
2
L - Lr[mm] 4
Modello classico del muscolo. Caratteristica dell’elemento contrattile
Il comportamento dinamico dell’elemento contrattile viene analizzato mediante prove di
contrazione isotonica postcaricata. In queste prove, per consentire l’uniformità delle
condizioni sperimentali, il muscolo viene stimolato in modo sovramassimale, in cui
cioè tutte le fibre muscolari possono essere considerate attive. Al muscolo viene
applicato un precarico Ti che serve a determinare la sua lunghezza iniziale Li; a tale
valore di Li si inducono una serie di contrazioni isotoniche con valori crescenti del
carico. La serie di prove è ripetuta partendo da differenti valori di lunghezza iniziale.
L’andamento dell’accorciamento in funzione del tempo presenta un tratto a velocità
costante che viene assunto come velocità di accorciamento del muscolo V alla
lunghezza iniziale Li e in corrispondenza alla forza T pari al valore del carico a cui è
stato sottratto il valore del precarico Ti. Si ottiene così, per ogni valore della lunghezza
iniziale un insieme di coppie Vn, Tn che può essere approssimata con:
10
T [g]
T0 - T
V=b
a+T
5
5
10
V[mm/s]
dove T0 è la forza per cui la velocità risulta
nulla, a e b sono parametri che possono
essere valutati dal fitting dei dati
sperimentali (b proporzionale alla lunghezza
iniziale ed a proporzionale alla forza T0).
Per diversi valori della lunghezza iniziale Li
si ottiene una famiglia di curve
Modello classico del muscolo. Caratteristica dell’elemento contrattile
CARATTERISTICA ATTIVA
La forza T0 può a sua volta essere espressa in funzione di
L, considerando che essa è la forza esercitata dal muscolo
a lunghezza L in condizioni isometriche e attivazione
sovramassimale. La T0(L) si può ottenere misurando la
forza massima esercitata in successive contrazioni
sovramassimali a lunghezze crescenti. Sottraendo alla
T0(L) la P(L) si ottiene il contributo del solo elemento
contrattile cioè la caratteristica attiva S0(L). Tale
caratteristica può essere approssimata con una parabola o,
per piccolo accorciamenti con una retta. Per contrazioni
non sovramassimali si assume che la caratteristica attiva
sia ancora pari alla S0(L) moltiplicata per una variabile di
controllo compresa tra 0 e 1.
T (g)
T0
S0
P(L)
1.
L / Lr
Poiché in una prova isotonica l’allungamento rimane pressoché costante, la velocità V coincide
praticamente con la velocità di accorciamento dell’elemento contrattile d/dt. Se poi si assume di
effettuare le prove per valori di lunghezza iniziale infinitamente vicini (Li coincidente con L) si
ottiene l’equazione caratteristica dell’elemento contrattile
P(L) e S0(L) sono funzioni note e si suppone sia
una funzione assegnata del tempo, d/dt fornisce
la velocità di accorciamento dell’elemento
contrattile in funzione di L, T e del tempo.
S0 –T + P
d
= bL
dt
aS0 + T- P
Modello classico del muscolo. Caratteristica dell’elemento serie
La caratteristica dell’elemento serie viene ricavata inducendo nel muscolo una contrazione
isometrica seguita da una contrazione isotonica. Ciò può essere effettuato portando il
muscolo ad una determinata lunghezza iniziale con un precarico (Lpr). Tale lunghezza viene
fissata in modo da impedire al muscolo qualsiasi allungamento (utilizzando una vite
micrometrica) ed il carico aumentato ad un valore Tp0. Si stimola quindi il muscolo in modo
sovramassimale. Questo si contrarrà, in una prima fase in modo isometrico e, quando la
forza attiva sviluppata eguaglierà il valore del carico in modo isotonico. Nell’istante di
passaggio tra le due fasi la d/dt dovrà risultare la stessa. Per cui eguagliando i valori di
d/dt ottenuti dall’equazione della contrazione isometrica e da quella della contrazione
isotonica si ottiene la:
dT/dt
Tp0
dS/dS* =
dL/dt
– dP/dL
Lpr
Lpr
I valori di dS/d per diversi valori di S* = Tp0 – P(Lpr) si dispongono secondo una retta.
Ciò permette un’approssimazione lineare:
dS/d=*(S + *)
che integrata fornisce la seguente espressione per la caratteristica elastica dell’elemento
serie:
S() = *[exp(*·) -1]
Limiti del Modello classico del muscolo.
• La funzione di attivazione (t) è una funzione empirica con valori compresi tra
0 e 1. Tale funzione non ha alcuna corrispondenza con i meccanismi fisiologici
che sottendono la contrazione e pertanto non è risultato possibile ricavare con
prove sperimentali un andamento della (t) che, in esperimenti simili ma
adottando metodi di misura diversi, fornisse lo stesso andamento temporale.
Risulta quindi necessario adottare un modello più complesso per la
rappresentazione dell’attivazione del muscolo.
• La caratteristica dell’elemento serie dipende dal livello di attivazione.
• Durante la contrazione possono evidenziarsi fenomeni di tipo inerziale che nel
modello di Hill (essendo gli esperimenti di tipo isotonico) possono essere
trascurati.
Modello strutturale della contrazione muscolare. Modello di Huxley.
Il modello di Huxely è un modello dall’interno della contrazione muscolare in
cui vengono considerati gli eventi elettrici a livello della membrana della cellula
muscolare e il meccanismo contrattile relativo allo scorrimento dei filamenti di
actina e miosina.
Il modello si puo’ quindi considerare costituito da due parti: una prima parte in
cui vengono rappresentati i fenomeni biochimici conseguenti alla
depolarizzazione della membrana cellulare e la generazione della
funzione di attivazione (t). La seconda parte del modello descrive
l’accoppiamento eccitazione-contrazione cioè lo sviluppo della forza
contrattile in seguito all’attivazione della cellula muscolare.
Modello strutturale della contrazione muscolare. Modello di Huxley.
Meccanismo di attivazione. Il modello dei meccanismi
di attivazione è un modello compartimentale costituito dai
tre compartimenti riprodotti in Figura dove vengono
rappresentati:
Un deposito interno di ioni Ca++, a concentrazione Ni.
Tale compartimento, durante la depolarizzazione rilascia
ioni Ca++ in quantità dipendente dal valore del potenziale
di membrana al di sopra di una soglia di polarizzazione.
Durante la fase di ripolarizzazione, in cui il potenziale della
membrana cellulare ritorna al valore di riposo, il
compartimento assume calcio fino al livello di riposo Ni0.
Superato tale livello il calcio in eccesso viene espulso
attivamente dalla cellula.
Il compartimento di attivazione, indicato con la variabile
che controlla la velocità di formazione dei ponti tra i
filamenti di actina e miosina. Durante la depolarizzazione
esso riceve ioni Ca++ dal compartimento Ni e dall’esterno
della cellula attraverso un flusso ICa.
Un compartimento Nr addetto alla rimozione del calcio
dalla fibra muscolare e al suo trasferimento al deposito Ni.
Durante la fase di depolarizzazione tale rimozione avviene a
una velocità estremamente ridotta, per cui questo ingresso
al compartimento Ni può in pratica essere trascurato.
J
Membrana
ICa
Ni
Nr
es
ec
ep
Modello strutturale della contrazione muscolare. Modello di Huxley.
Fase di depolarizzazione
dNi/dt = -K(eE – 1) Ni
dNr/dt = F
F1
J
d/dt = - + K(eE – 1)Ni + Ca ICa
Membrana
E è il livello del potenziale di membrana sopra la
soglia di depolarizzazione e ICa è generalmente
rappresentato con una funzione empirica di E.
Fase di ripolarizzazione
dNi/dt = rNr – J
dNr/dt = - rNr +
d/dt = -
J uguale a zero per NiNi0 e uguale a rNr per
NiNi0.
Le condizioni iniziale sono definite dai valori delle
variabili compartimentali alla fine della fase
precedente. Se si parte da uno stato di riposo
Ni0(0)=Ni0 Nr(0)=0 e (0)=0.
ICa
Ni
Nr
es
ec
ep
Modello strutturale della contrazione muscolare. Modello di Huxley.
Accoppiamento eccitazione-contrazione
L’accoppiamento eccitazione-contrazione si realizza attraverso
l’intervento di due proteine associate all’actina: la troponina e
la tropomiosina. A basse concentrazioni dello ione Ca++ nel
sarcoplasma la troponina inibisce la formazione di legami tra
actina e miosina. Al crescere della concentrazione, oltre una
data soglia, il Ca si lega alla troponina rimuovendo l’effetto
inibitorio. Le molecole di actina possono così legarsi ai
filamenti di miosina in siti preferenziali. Poichè questi legami
hanno un verso preferenziale, che è quello dell’accorciamento
della fibra, la contrazione si verificherà per un successivo
formarsi e disconnettersi di questi legami. Con riferimento alla
figura indichiamo con n(t,x) la percentuale di siti legati
all’istante t a distanza x. La variazione di questa percentuale
all’istante t si può scrivere come:
n/ t=(1-n)f - ng
dove f è la probabilità per unità di tempo della formazione di
un legame mentre g è la probabilità per unità di tempo della
rottura di un legame
miosina
actina
o
x
Modello strutturale della contrazione muscolare. Modello di Huxley.
Nell’ipotesi che la dipendenza di n da t sia solo attraverso x si ha:
-v·n/x=f-(f+g)·n
dove v è la velocità di scorrimento dei filamenti di actina e miosina.
Se s è la lunghezza del sarcomero e V’ è la velocità di
accorciamento del muscolo normalizzata rispetto alla sua
lunghezza, v sarà uguale V’·s/2. Dove f e g sono date dalle relazioni
empiriche di figura.
La soluzione dell’equazione fornisce la relazione tra n ed x durante
contrazioni con velocità di accorciamento ed attivazioni costanti.
Per 0 x h si ottiene :
dn/dx= [( f1 + g1)n – f1] 2x/(hsV’)
Integrando si ha: n(x)=
dove =h·(f1+g1)/s.
f1
f1 + g1
n(h)=0
[1-exp((x2/h2-1)/V’)]
f
1
x/h<0
f=0
0≤x/h≤1
f=(t)f1 x/h
x/h>0
f=0
g
Per x<0 imponendo una condizione di continuità con la soluzione
precedente si ottiene:
n(x)=
per x>h
f1
f1 + g1
1
(1-exp(-/V’)) exp(2g2x/sV’)
n=0.
x/h
x/h
x/h<0
g=g2
x/h≥0
g=g1 x/h
Modello strutturale della contrazione muscolare. Modello di Huxley.
Per determinare una relazione tra la velocità V’ e la forza S generata dal muscolo (a meno
della componente passiva), si consideri che la forza totale è la somma delle forze generate
dai legami attivi di metà sarcomero. Se c è una costante legata alla densità di questi legami e
se K è la costante elastica la forza S è data da:
S=cK n(x) x dx
L’integrale va ovviamente calcolato dove n(x)0
Utilizzando le espressioni ricavate per n(x) si ottiene l’espressione:
S=cK f1 /( f1 + g1) [1-V’ (1-e-/V’) )(1+0.5V’ ( f1 /( f1 + g1) ]
che ha significato e forma analoghe all’equazione di Hill.
Modello strutturale della contrazione muscolare. Modello di Huxley.
E
Le equazioni del modello di Huxley
consentono il calcolo della forza
attiva S sviluppata dal muscolo.
Nel caso di una contrazione
isometrica (L=cost) gli andamenti di
ed S in funzione del tempo per
differenti valori della frequenza dei
treni di impulsi di depolarizzazione
della membrana sono rappresentati
in figura.
S
t
Un parallelo tra i due modelli può essere ottenuto considerando la figura dove =M-H=2C-I è l’area
di sovrapposizione tra i filamenti di actina e miosina. La lunghezza L del sarcomero quando non è
presente l’allungamento elastico è: L=M+I=M+2C-δ. Quando invece è presente l’allungamento
elastico è: L=M+I+=M+2C-+=Lcr-+. Differenziando la lunghezza del sarcomero rispetto al
tempo si ottiene:
dL/dt=-d/dt+d/dt
ricordando che il termine M+2C rappresenta la somma delle lunghezze del filamento di miosina e dei
due filamenti di actina ed è quindi un termine costante.
Poichè nel modello di Hill la forza è la somma dei contributi dell’elemento serie e dell’elemento
parallelo e la è una funzione della lunghezza del sarcomero (s) che può essere espressa in funzione
di e si può scrivere T= P(L)+S(,). Derivando la forza totale rispetto al tempo si ottiene la:
dT/dt = dP/dt + dS/dt
Anche quest’equazione coincide con l’equazione ottenuta con il modello dall’esterno
Miosina
Actina
L
I/2
I/2
M
/2
H
C
/2