Modellazione Solida
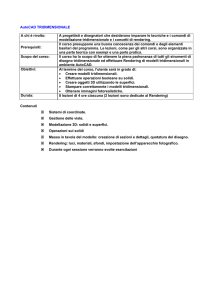
Superfici in 2D 3D non definiscono sempre un volume.
In molte applicazioni é necessario definire solidi.
Collezioni di linee, curve e superfici non necessariamente definiscono solidi.
Esempio:
Solidi e Rendering
Informatica grafica
1
Proprietà Rappresentazione
Dominio generale: permette la rappresentazione di
molti solidi significativi.
Completa (non ambigua): ad ogni rappresentazione
corrisponde uno ed un solo solido.
Univoca: ogni solido ha una sola rappresentazione.
Accurata: permette di trovare rappresentazioni senza
approssimare.
Vieta rappresentazioni non valide.
Preserva la chiusura: le trasformazioni non rendono
la rappresentazione non valida.
Ammette algoritmi efficienti.
Solidi e Rendering
Informatica grafica
2
Operazioni Booleane su
Solidi
Oggetti possono essere combinati (per formare
oggetti più complessi) usando operatori booleani
insiemistici. Il problema è che il risultato non é
sempre un solido:
Solidi e Rendering
Informatica grafica
3
Operatori Booleani
Regolarizzati
* —* danno sempre come risultato un solido
A * B = closure (interior ( A B))
interior = solido - frontiera
closure = solido + frontiera
Esempio:
Solidi e Rendering
Informatica grafica
4
Esempio
Intersezione :
la frontiera comune ( C-D ; A-B) appartiene al solido
se l’interno dei 2 oggetti é dalla stessa parte (A-B).
Non appartiene se sono dalla parte opposta (C-D)
Solidi e Rendering
Informatica grafica
5
Operatori Generali
Operatori su interno e boundary
Posso ora definire gli operatori regolarizzati:
A B = (Ai Bi) (Ab Bi) (Bb Ai ) ( Ab Bb same)
Solidi e Rendering
Informatica grafica
6
Primitive Instancing
Il sistema definisce insieme di primitive parametriche.
Utile per definire oggetti complessi difficili da ottenere
per combinazione di oggetti più semplici. Usato nel
CAD.
Esempio:
Solidi e Rendering
Informatica grafica
7
Sweep Representations
Definiti da una figura 2D ed una traiettoria (generalmente
lineare o circolare).
General sweeps: il profilo si modifica lungo la traiettoria
curvilinea.
General Sweeps difficili da modellare.
Difficile applicare operazioni booleane.
Unione di 2 sweeps non é necessariamente una sweep
(semplice).
Solidi e Rendering
Informatica grafica
8
Boundary Representations
B-Reps
Oggetto descritto in termini delle superfici esterne,
vertici, lati e facce.
Spesso le superfici esterne sono planari e poligonali
(triangolari).
Superfici curve sono difficili da trattare.
Spesso si assume che le superfici di frontiera siano
2-manifold.
Solidi e Rendering
Informatica grafica
9
Poliedri
Solido le cui superfici sono poligoni. I vertici appartengono
ad un numero pari di poligoni (2 se 2-manifold).
Poliedro semplice: non ha buchi.
La B-REP di un poliedro semplice soddisfa la formula di
Eulero:
V-E+F=2 (Se ci sono buchi vale V-E+F-H=2(C-G) )
dove H:n. buchi C: n. compon. G: buchi che attraversano l’oggetto.
Solidi e Rendering
Informatica grafica
10
Ulteriori Vincoli
Soddisfare la formula di Eulero non è sufficiente.
Dobbiamo anche imporre :
1) ogni lato connette 2 vertici
2) ogni lato é condiviso da 2 facce
3) in ogni vertice entrano almeno 3 lati
4) le facce non devono tagliarsi
Gli operatori di Eulero modificano un oggetto ma senza
violare la formula.
Operazioni che muovono vertici, lati e facce si chiamano
tweak.
Solidi e Rendering
Informatica grafica
11
Operazioni Booleane
Applicando operatori regolarizzati a B-Reps otteniamo
B-Reps.
Per calcolare l’intersezione bisogna ispezionare tutti i
poligoni dei 2 oggetti (A B) e per ogni poligono p di
A verificare se:
1) pAB Bi
2 ) pAB - B
3 ) pAB BB same oppure pAB BBdiff
per determinare quale è la situazione si usano
tecniche di ray-tracing.
Solidi e Rendering
Informatica grafica
12
Spatial Partitioning
Decomposizione di un solido in molti solidi più semplici
non necessariamente uniformi tali che i solidi siano
contigui, non intersecanti e di un tipo più semplice.
Le rappresentazioni più usate sono:
Cell decomposition
Spatial-occupancy enumeration
Octrees
Binary space partitioning trees
Solidi e Rendering
Informatica grafica
13
Cell Decomposition
Insieme di celle primitive (spesso parametriche e
curve). Oggetti complessi definiti dall’unione di
celle primitive. Rappresentazione non-ambigua ma
non univoca. Esempio:
Solidi e Rendering
Informatica grafica
14
Spatial-Occupancy
Enumeration
Insieme di celle tutte uguali arrangiate in modo
regolare. Le celle sono dette voxels. Tipicamente i
voxels sono cubi. Rappresentazione non-ambigua e
univoca.
Problema principale è l’approssimazione implicita
nella rappresentazione. Altro svantaggio è l’alto
uso di memoria.
Solidi e Rendering
Informatica grafica
15
Octrees
Octrees: variante gerarchica di spatial-occupancy. Sono
l’estensione 3D dei Quadtrees.
Idea base: partizione binaria, ogni area può essere piena,
vuota o parzialmente piena. La migliore
rappresentazione è con alberi di arietà 4 (8 in 3D).
Solidi e Rendering
Informatica grafica
16
Quadtrees
Spazio diviso in quadranti. Esempio di struttura
dati:
Solidi e Rendering
Informatica grafica
17
Octrees (2)
Lo spazio viene diviso in 8 ottanti numerati da 0 a 7
In generale: il numero dei è nodi proporzionale alla
superficie. Dipende solo dall’estensione della
frontiera, non dal solido.
Solidi e Rendering
Informatica grafica
18
Operazioni Booleane Su
Quadtrees (Octrees)
Danno sempre risultati
rappresentabili. Molto
efficienti e facili da
realizzare.
Solidi e Rendering
Informatica grafica
19
Neighbor Finding
Come trovare il vicino che sta sopra A ?
Risalgo da A fino a trovare il primo antenato comune
(1), poi scendo verso B (2):
(1) risalgo fino al primo nodo a cui arrivo da sud
(2) ridiscendo in modo speculare fino a trovare una
foglia
Solidi e Rendering
Informatica grafica
20
Binary Space Partitioning
Trees
Dividono lo spazio in sottospazi, definendo un piano
arbitrario Ad ogni nodo è associato un piano. Il figlio
sinistro è “dietro” il piano, il destro “davanti”.
Efficiente per decidere se un punto é interno o no ad un
solido. Esempio in 2D :
Solidi e Rendering
Informatica grafica
21
Constructive Solid Geometry
L’oggetto è albero in cui:
» Nodi : operatori (booleani,
trasformazioni)
» Foglie : primitive
Se le primitive sono semplici si
può realizzare efficientemente,
più delle B-Reps.
Solidi e Rendering
Informatica grafica
22
CSG (2)
In CSG le rappresentazioni non sono univoche. Questo
può creare dei problemi se l’utente può modificare
interattivamente il disegno. Esempio:
Solidi e Rendering
Informatica grafica
23
Confronto
Accuratezza
NO
SI
Generalità
NO
Univocità
SI
NO
Solidi e Rendering
spatial -partitioning
B-Reps poliedriche
CSG primitive complesse
B-Reps non poliedriche
primitive instancing
primitive instancing
sweeps
octrees
spatial occupancy
altri
Informatica grafica
24
Confronto (2)
Validazione
Chiusura
Compattezza/
Efficienza
Solidi e Rendering
difficile per B-Reps
semplice per altri
NO sweeps, primitive instancing
SI
altri
CSG compatto non molto efficiente
octrees e spatial occupancy poco
compatti ma efficienti
Informatica grafica
25
Migliorare Realismo
Obiettivo : costruire immagini che diano molte
informazioni sull’oggetto modellato.
Possibilità: creare immagini fotorealistiche,
aggiungere effetti speciali.
Immagini realistiche sono spesso indispensabili:
Progettazione di macchine, aerei, .......
Visualizzazione di processi fisici, chimici ....
Videogiochi.
Simulatori.
Sistemi per l’insegnamento.
Solidi e Rendering
Informatica grafica
26
Difficoltà
Il mondo é molto complesso: creare un modello
completamente accurato é difficile, visualizzarlo può
essere molto costoso.
Nostro goal: L’immagine deve contenere abbastanza
informazioni da far comprendere le relazioni 3D tra gli
oggetti.
Se le relazioni sono semplici, bastano immagini non
dettagliate.
Esempio: quale casa é davanti?
Solidi e Rendering
Informatica grafica
27
Problema
Le proiezioni in 2D di oggetti
3D perdono molte
informazioni generando
ambiguità. Come é orientato
il cubo a?
a
b
c
Per risolvere spesso sfruttiamo
la nostra conoscenza
dell’oggetto. A volte, però,
non basta. E’ il sopra di una
scala oppure il sotto ?
Solidi e Rendering
Informatica grafica
28
Rendering di Linee
Molte tecniche aiutano a migliorare l’immagine:
Viste ortografiche multiple.
Proiezioni prospettiche.
Depth cueing.
Depth clipping.
Textures, colore ed eliminazione linee nascoste.
Solidi e Rendering
Informatica grafica
29
Viste Ortografiche Multiple
L’uso di viste ortografiche multiple è utile per oggetti
semplici, ma non è facile da interpretare per oggetti
molto complessi
Esempio:
color plate II. 24
Solidi e Rendering
Informatica grafica
30
Proiezioni Prospettiche
Rendono meglio la distanza, ma non sempre sono non
ambigue. A sinistra abbiamo un cubo o un tronco di
piramide? La casa di sinistra é più piccola o più
lontana. Trovare il punto di fuga di lati paralleli
aiuta a eliminare le ambiguità.
Solidi e Rendering
Informatica grafica
31
Depth Cueing
Oggetti più lontani vengono disegnati meno intensi.
Normalmente è realizzato definendo un depth-cue
color (background) poi l’intensità del colore di un
oggetto si ottiene interpolando il suo colore proprio con
il depth-cue color.
In PHIGS+ abbiamo:
front, back depth-cue planes
scale factor per ogni piano
davantifront color, dietro back color, in mezzo
interpola front_color_back.
Molto efficace per disambiguare oggetti lontani. Poco
utile per oggetti vicini.
Solidi e Rendering
Informatica grafica
32
Depth Clipping
Definendo un back clipping plane gli oggetti lontani
sono (parzialmente) tagliati.
Può essere visto come una variante di depth-cueing.
Alternativa : invece di tagliare, evidenziare le
intersezioni con il back clipping plane. Effetto molto
utile se il back clipping plane viene fatto muovere.
Solidi e Rendering
Informatica grafica
33
Altre Tecniche
Texture:
applicare sulle superfici disegni o griglie fitte.
Può risolvere molte ambiguità, é utile soprattutto nelle
proiezioni prospettiche.
Colore:
assegnare ad ogni oggetto un colore diverso.
Il colore può essere proporzionale alla profondità.
Eliminazione linee nascoste:
rimozione delle linee coperte da superfici più vicine.
Aumenta il “realismo” ma nasconde molte relazioni tra
oggetti.
Alternativa: mostrare le linee nascoste ma in modo diverso
(tratteggiate).
Solidi e Rendering
Informatica grafica
34
Rendering di Immagini con
Ombre
Su terminali raster possiamo visualizzare immagini
ombreggiate. Le tecniche usate sono:
Rimozione parti nascoste
Uso degli effetti di luce
Interpolated shading
Modellazione delle proprietà dei materiali
Uso di textures
Ombre
Trasparenza e riflessione
Effetti fotografici
NOTA: tecniche semplici possono però dare problemi di aliasing.
Solidi e Rendering
Informatica grafica
35
Rimozione Superfici ed
Effetti di Luce
Rimozione di superfici nascoste: con superfici opache la
rimozione é indispensabile per disambiguare l’immagine.
Illuminazione: per evitare di avere oggetti “piatti” si
definiscono sorgenti di luce. Tipi di luce:
» Luce ambiente: proviene da tutte le direzioni e produce la
stessa illuminazione su tutti gli oggetti.
» Sorgente uniforme: approssima la luce di una lampadina.
» Sorgente direzionale: approssima la luce solare, è una
sorgente posta all’infinito (raggi paralleli).
Effetti di Luce: superfici perpendicolari più intense, quelle
più oblique meno illuminate.
Solidi e Rendering
Informatica grafica
36
Altre Tecniche
Ombreggiatura con interpolazione: l’ombreggiatura é
calcolata ad ogni vertice di ogni oggetto, migliora
l’aspetto di superfici curve (Gouraud) approssimate con
poliedri.
Proprietà dei materiali: tenere in conto come riflettono
la luce (Phong).
Modelli avanzati per la luce: usano modelli più
rispondenti alle proprietà fisiche della luce. Spesso
molto difficili da implementare efficientemente.
Texture, Ombre, Trasparenza e Riflessione, Uso
della Profondità di Campo: permettono di creare
immagini molto realistiche
Solidi e Rendering
Informatica grafica
37
Animazione
Il realismo di un’animazione è molto diverso da quello
di un’immagine:
Minore importanza della fedeltà del modello.
Cura al realismo dl movimento.
Riduzione del temporal-aliasing (effetto ruote di
una macchina).
Solidi e Rendering
Informatica grafica
38
Visione Stereo
Generare immagini diverse per i 2 occhi migliora
molto l’effetto di profondità. Però richiede dei visori
speciali (es. occhiali).
Solidi e Rendering
Informatica grafica
39
Eliminazione Superfici
Nascoste
Problema fondamentale: efficienza.
In molti computers l’operazione viene fatta in hardware.
Ci sono due approcci fondamentali:
image precision riferimento è l’immagine sullo schermo.
object precision riferimento sono oggetti nel loro mondo.
Pseudocodice image precision:
for (ogni pixel dell’immagine)
{
determina l’oggetto più vicino all’osservatore che è
visibile attraverso il pixel;
disegna il pixel nel colore opportuno;
}
Solidi e Rendering
Informatica grafica
40
Object Precision
Pseudocodice object-precision
for (ogni oggetto del mondo)
{
determina le parti dell’oggetto non coperte da altri
oggetti;
disegna queste parti nel colore opportuno;
}
Se n= numero oggetti e P= numero pixels
costo image precision
O(np)
costo object precision
O(n2)
Solidi e Rendering
Informatica grafica
41
Tecniche Generali
Problema: algoritmi di image-precision e di object
precision sono molto inefficienti.
Soluzione: sfruttare la coerenza delle figure per
semplificare (evitare) i conti. Ci sono molti tipi di
coerenze che si possono sfruttare per calcolare i valori
incrementalmente e non sempre da zero.
Solidi e Rendering
Informatica grafica
42
Coerenza
Oggetto: separazione tra oggetti sep. componenti (facce,
lati).
Faccia: proprietà cambiano con regolarità.
Lato: la visibilità cambia solo se ci sono intersezioni.
Lato implicato: se 2 facce si intersecano la linea di
intersezione si calcola da solo 2 punti.
Scan line: oggetti incontrati variano poco da una linea alla
successiva.
Area: un gruppo di pixels è spesso coperto dalla stessa area.
Profondità: parti adiacenti cambiano poco in profondità.
Frame: 2 frames consecutivi sono molto simili.
Solidi e Rendering
Informatica grafica
43
Trasformazioni Prospettiche
La determinazione delle superfici
visibili va fatta in 3D.
Operazione fondamentale è
verificare se un punto copre un
altro. Accade solo se sono
allineati e la verifica richiede 4
divisioni:
X1/Z1=X2/Z2 Y1/Z1=Y2/Z2
Più efficiente se proiezioni
parallele:
X1=X2
Y1=Y2
Solidi e Rendering
Informatica grafica
44
Trasformazioni Prospettiche
Soluzione: ridurre la piramide canonica nel cubo
canonico. La trasformazione preserva il risultato. La
matrice di conversione M vale:
0
0
1 0
0 1
M
0 0
0 0
Solidi e Rendering
Informatica grafica
0
1
(1 z min )
1
0
z min
(1 z min )
0
45
Esempio
Trasformando un cubo si ottiene:
Solidi e Rendering
Informatica grafica
46
Estensioni e Volumi
Delimitanti
Conoscere l’ estensione di oggetti e le loro proiezioni
evita molti conti inutili. Assumendo di avere già
normalizzato, se l’estensione delle proiezioni non si
sovrappone è inutile vedere se gli oggetti si coprono.
Solo se l’ estensione si sovrappone potrebbero coprirsi.
Solidi e Rendering
Informatica grafica
47
Bounding Box e Volume
Ad ogni oggetto possiamo associare:
Bounding volume (3D) dipende solo dall’oggetto.
Bounding box (2D) dipende dalla proiezione.
Per determinare la sovrapposizione (non copertura)
spesso basta l’estensione 1D. Extents e Bounding
volumes sono anche usati per determinare se un
raggio interseca l’ oggetto.
Solidi e Rendering
Informatica grafica
48
Back-Face Culling
Nei poliedri é utile identificare le facce
nascoste all’osservatore.
In coordinate normalizzate:
back_face normale uscente ha Z<Ø
Le backfaces si possono scartare, se il
poliedro non é clippato. Eliminando le
backfaces si riducono di circa la metà
i poligoni da considerare.
Solidi e Rendering
Informatica grafica
49
Partizionamento Spaziale
Idea: dividere lo spazio ed assegnare ad ogni sottospazio
una parte degli oggetti.
Vantaggi: confronti tra oggetti molto ridotti.
Problema: non sempre possibile dividere bene lo
spazio.
Per ovviare a questo prolema si usano tecniche di
partizionamento adattivo. Vedremo poi degli esempi.
Solidi e Rendering
Informatica grafica
50
Gerarchie
Strutture gerarchiche spesso permettono di capire
velocemente se 2 oggetti non si coprono
(intersecano).
Esempio:
Solidi e Rendering
Informatica grafica
51
Z-Buffer Algorithm
E’ un algoritmo di image-precision.
Di facile implementazione hardware/software.
Richiede in memoria uno Z-buffer oltre al frame buffer.
Non è necessario ordinamento tra poligoni.
Non c’é alcun confronto tra oggetti.
La scan conversion può essere effettuata una riga per
volta (nessuna interazione diretta).
Solidi e Rendering
Informatica grafica
52
PseudoCodice
void zBuffer()
{ int pz; /*Polygon's z at pixel coords (x, y)*/
for ( y = 0; y < YMAX; y++ ) {
for ( x = 0; x < XMAX; x++ ) {
WritePixel(x, y, BACKGROUND_VALUE);
WriteZ(x, y, 0);
}
}
for ( each polygon ) {
for ( each pixel in polygon's projection ) {
pz = polygon's z-value at pixel coords (x, y);
if ( pz >= ReadZ(x, y)) { WriteZ(x, y, pz);
WritePixel(x, y, polygon's color at pixel coords
(x, y));
}}}
}
Solidi e Rendering
Informatica grafica
53
Esempio Z-Buffer
Costruzione incrementale di 1 poligono per volta.
Problema : calcolo delle scan lines può essere costoso.
Idea: sfruttare depth coherence per semplificare.
Poligoni sono planari Ax+By+Cz+D=Ø quindi
z=[-D-Ax-By]/C ma incrementalmente:
z1=[-D-Ax1-By1]/C z2=[-D-A(x1+x)-By1]/ C=z1-[A/C] x
Solidi e Rendering
Informatica grafica
54
Alternativa
Il valore di z su una scan line viene calcolato per
interpolazione.
Esempio:
Solidi e Rendering
Informatica grafica
55
Vantaggi e Svantaggi
Vantaggi
Molto generale non richiede che gli oggetti siano
poliedrici.
Facilmente implementabile. E’ incrementale, salvando
lo z-buffer é facile tenere conto di nuovi oggetti.
Varianti dello z-buffer si applicano anche a solidi CSG.
Svantaggi
Richiede molta memoria(~4 byte per pixel).
Soffre di problemi di aliasing, a volte ci sono
imprecisioni ai bordi dei poliedri.
Solidi e Rendering
Informatica grafica
56
Scan-Line Algorithms
Generalizzazione a 3D, si applica ad un insieme di
poligoni contemporaneamente. Si mantengono una
Edge Table come in 2D ed una Polygon Table con:
1) Equazione del piano
2) Informazioni su colore ed illuminazione
3) Flag booleano (In / Out)
La Active Edges Table contiene le stesse informazioni
del caso 2D.
Quando si attraversa un lato il flag del suo poligono
viene flippato. Se il punto appartiene a più poligoni
bisogna calcolare le z.
Solidi e Rendering
Informatica grafica
57
Esempio
Solidi e Rendering
Informatica grafica
58
Casi Particolari
Caso di prima visto in 3D.
Se i poligoni non si tagliano,
quando incontra in uscita
ABC non c’é bisogno di
confrontare z.
Per evitare le intersezioni
conviene “splittare” i
poligoni.
Solidi e Rendering
Informatica grafica
59
Generalizzazione
Gli algoritmi di Z-buffer e di scan-line possono essere
generalizzati a superfici più complesse:
add surfaces to surface table;
initialize active-surface table;
for( each scan line ) {
update active-surface table;
for( each pixel on scan line ) {
determine surfaces in active-surface table that
project to pixel;
find closest such surface;
determine closest surface's shade at pixel;
}
}
Solidi e Rendering
Informatica grafica
60
Ray Tracing
Idea: tracciare un raggio dal centro attraverso ogni
pixel e calcolare cosa interseca prima. Facile da
implementare.
Solidi e Rendering
Informatica grafica
61
Pseudocodice
select center of projection and window on viewplane;
for( each scan line in image ) {
for( each pixel in scan line ) {
determine ray from center of projection through pixel;
for( each object in scene ) {
if(object is intersected and is closest considered thus far)
record intersection and object name;
}
set pixel's color to that at closest object intersection;
}
}
Solidi e Rendering
Informatica grafica
62
Calcolo Intersezioini
Centro (Xø,Yø,Zø) punto di vista
Pixel (X1,Y1,Z1) centro del pixel
retta : X=Xø+t ²X
²X=X1-Xø
Y=Yø+t ²Y
²Y=Y1-Yø
Z=Zø+t ²Z
²Z=Z1-Zø
Esempio con la sfera centro (a,b,c)
raggio r
(X-a)2+(Y-b) 2 +(Z-c) 2 = r 2
Sostituendo otteniamo:
(²X 2 +²Y 2 +²Z 2)t 2 +[²X(Xø-a)+²Y(Yø-b)+²Z(Zø-c)]2t+(Xø-a) 2+ +(Yø-b)
2 +(Z -c) 2 -r 2 =ø
ø
Calcolata l’ intersezione X Y Z calcoliamo la tangente. Serve per il
colore.
Per la sfera abbiamo: ( [X-a] /r [Y-b] /r [Z-c] /r )
Solidi e Rendering
Informatica grafica
63
Intersezioni con Poligoni
Fatta in 2 passi :
1) intersezione raggio e piano
poligono.
2) verifica che sia interna al
poligono.
Piano : Ax+By+Cz+D=0
Sostituendo:
t=-[Axø+Byø+Czø+D]/[A²x+B²y+C²z]
test contenimento fatto in 2D :
proiezione ortografica + test
Solidi e Rendering
Informatica grafica
64
Efficienza di Ray Tracing
Schermo : 1024x1024 pixels
Oggetti : 1000 109 intersezioni da calcolare
Soluzioni
1) trovare formule più semplici per calcolare
intersezioni.
2) usare bounding volumes semplici da testare come
sfere o insiemi di piani paralleli (slabs).
3) usare gerarchie. Quelle definite nella modellazione
oppure definite apposta per semplificare il rendering.
4) partizionamento spaziale: controlla l’intersezione
solo con oggetti nei volumi attraversati dal raggio.
Solidi e Rendering
Informatica grafica
65
Partizionamento Spaziale
Metodo semplice : dividere
lo spazio in parti uguali.
Migliora l’ efficenza.
Metodi più complessi
usano un partizionamento adattivo.
Solidi e Rendering
Informatica grafica
66
Liste di Priorità
Idea : trovare un ordinamento di visibilità degli oggetti e
poi disegnarli in ordine (Object precision). Ci sono
molte varianti.
Problema : non sempre possibile senza modificare figura
Esempio:
si
no
Solidi e Rendering
Informatica grafica
67
Depth Sort
Algoritmo base: ordinare i poligoni rispetto alla
profondità. Passi fondamentali:
1) Ordinare per z (minima) crescente.
2) Risolvere le ambiguità (eventualmente splittando).
3) Fare la scan-conversion (back to front).
Per risolvere il punto 2 verifichiamo se: Le estensioni
su x (y o sul piano xy) si sovrappongono, oppure se
esiste un piano (di uno dei loro poligoni) che li
separa. Se ancora non riusciamo a risolvere le
ambiguità dobbiamo tagliare un poligono con il
piano di un altro.
Solidi e Rendering
Informatica grafica
68
Esempio
Nel caso a sinistra P sta tutto da na parte rispetto a
Q. Nel caso a destra Q sta tutto da una parte
rispetto a P.
Solidi e Rendering
Informatica grafica
69
Binary Space-Partitioning Trees
Calcola informazioni di visibilità indipendenti dal punto
di vista. Utile se dobbiamo fare più proiezioni.
Idea: selezionare un poligono e dividere tutti gli altri in
due gruppi: Front e Back, in funzione della loro
posizione (eventualmente splittando). La costruzione
poi continua ricorsivamente per entrambi i gruppi.
Conoscendo il viewpoint posso facilmente visitare il
BSP in ordine back to front. Richiede un
preprocessing costoso ma riutilizzabile per molte
proiezioni.
Solidi e Rendering
Informatica grafica
70
Area-Subdivision Algorithms
Idea : suddividere il piano di proiezione fino a che é
immediato decidere chi è visibile in ogni area
Algoritmo di Warnock divide l’area in 4 parti uguali
ed ad ogni passo la relazione tra immagine e
poligono può essere:
Solidi e Rendering
Informatica grafica
71
4 Casi Semplici
1) nessun poligono interseca l’area (background).
2) un solo poligono interseca o é contenuto
(background+scan-conversion poligono).
3) un solo poligono contiene l’area (colore poligono).
4) un poligono contiene ed è davanti agli altri che
intersecano o sono contenuti o contengono (colore
poligono).
Il caso 4 può essere verificato confrontando le z nei
quattro estremi. Se non siamo in questi casi
continuiamo a dividere.
Solidi e Rendering
Informatica grafica
72
Esempi
Solidi e Rendering
Informatica grafica
73
Algoritmi per Superfici Curve
Solo z-buffer per ora tratta le superfici curve. Gli altri
richiedono di approssimare le superfici con facce
poligonali.
Un altro algoritmo per superfici bicubiche è quello di
Catmull (generalizzazione di Warnock).
Idea : Suddividere i patches in subpatches fino a che
siamo in una situazione ovvia.
Solidi e Rendering
Informatica grafica
74
Scan-Line
di Superfici Curve
for( each patch ) {
push patch onto stack;
while( stack not empty ) {
pop patch from stack;
if( patch covers <= 1 pixel ) {
if( patch's pixel closer in z )
determine shade and draw;
}
else { subdivide patch into 4 subpatches;
push subpatches onto stack;
}
}
}
Solidi e Rendering
Informatica grafica
75
Confronto Metodi
In generale : algoritmi di object-precision vanno bene
con scene semplici mentre quelli in image-precision
dipendono poco dal numero di oggetti.
Non esiste un metodo ottimo, dipende
dall’applicazione. Il vantaggio di Z-buffer é la sua
semplicità e generalità. Il Raytracing viene usato
solo se si vogliono ottenere immagini di alta qualità.
Solidi e Rendering
Informatica grafica
76