elettricamente come

3. Il motore di Carnot
Poiché, come si è visto, un motore funzionante va raffreddato, si potrebbe pensare che, in fin dei
conti, a causa del riscaldamento per effetto degli attriti, parte dell’energia si disperde e quindi non
tutto il calore assorbito può essere trasformato in lavoro. Non è però questa una formulazione
corretta del punto fondamentale.
Dire che i motori disperdono per attrito significa che essi cedono calore alle varie sorgenti fredde
che li circondano: aria, acqua, strutture metalliche del motore stesso.
I primissimi motori termici, proprio a causa delle dispersioni, avevano un bassissimo rendimento.
Ad esempio la macchina a vapore dell’ingegnere inglese T. Newcomen (1705) aveva   0.005 .
Che è come dire che il 99.95 per cento dell’energia andava sprecato. Un poco meglio, ma sempre
fiacca, quella dello scozzese J.Watt (1763), il quale, portando il meccanismo di raffreddamento
fuori dal motore, riuscì a far salire  fino a 0.04. Le macchine attuali sono decisamente migliori,
tuttavia anche una moderna centrale nucleare non supera di molto   0.35 . Il 65 per cento del
calore sprigionato dalle reazioni nucleari se ne va a riscaldare i pesci del lago.
Ma quanto è ampio il margine di miglioramento? Come formalizzare quanta parte di questo
rendimento così basso è ineliminabile, intrinseca, legata a doppio filo alle leggi inesorabili della
natura? Per rispondere a questa domanda fondamentale, Sadi Carnot cominciò a concepire una
serie di astrazioni per isolare il problema principale. Anziché costruire un motore, si limitò
semplicemente a pensarlo e lo costruì soltanto con carta e penna. E già che c’era, lo fece davvero
bene: concepì il motore migliore del mondo: quello che oggi viene denominato il ciclo di Carnot.
Tramite esso voleva mostrare quale fosse il rendimento del miglior motore che possiamo
immaginare.
Ma vediamole una per una queste astrazioni. Primo problema: quando si esegue una trasformazione
termodinamica, in generale il processo è turbolento, risulta impossibile definire, ad esempio, un
valore univoco della pressione e un valore univoco della temperatura per un gas contenuto in un
recipiente durante una trasformazione. Detto in altri termini, non capita mai che durante una
trasformazione un aeriforme sia sempre in equilibrio: in generale in un punto esso avrà una
temperatura e un poco più in alto una temperatura diversa, in una zona una certa pressione e più in
alto una pressione differente.
Carnot concepì delle trasformazioni, puramente immaginarie, dove questo problema non sussiste. Il
sistema non evolve in maniera turbolenta, ma passando attraverso una serie infinita di stati di
equilibrio: posso, cioè, definire sempre le variabili di stato durante la trasformazione. Tali tipi di
trasformazioni immaginarie sono dette quasistatiche. Solo esse hanno la proprietà di poter essere
espresse da delle equazioni (tipo PV  k , PV   k etc) e rappresentate con delle linee nel piano
PV.
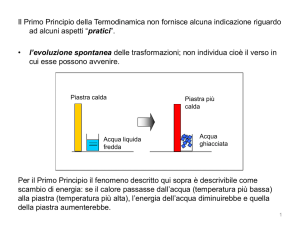
Secondo problema: nelle trasformazioni reali ci sono degli effetti irreversibili. Che significa
irreversibili? Bhe, che non si può tornare indietro cancellando le tracce di quello che è accaduto.
Ad esempio se brucio della carta lascio una serie di indizi nell’ambiente: modifiche strutturali della
carta, riscaldamento, che non posso poi cancellare in modo semplice. Altro esempio: strofino le
mie mani l’una contro l’altra e queste si riscaldano. Dopo, però, non posso certo strofinarle al
contrario facendole raffreddare e riprendermi, per così dire, il lavoro fatto durante lo strofinio.
Dalle dissipazioni per attrito non si torna indietro. Tutti effetti dissipativi, effetti cioè di
riscaldamento, dovuti non a somministrazione di calore, ma, per esempio, ad attrito, viscosità e
anelasticità: essi sono chiaramente irreversibili. Così pure, è irreversibile lo spostamento spontaneo
di calore per conduzione da un corpo caldo a un corpo freddo. Il termine «dissipativo» sta ad
indicare che l’energia subisce una sorta di degradazione, passando da forme più utilizzabili per la
produzione di lavoro macroscopico a forme meno utilizzabili.
Il problema sono gli effetti dissipativi? Le trasformazioni termodinamiche concepite da Carnot
per il suo motore ideale sono anche senza dissipazione. Senza attriti. Si tratta divertirsi un poco,
almeno con la fantasia: se dobbiamo creare il motore migliore del mondo le trasformazioni che
segue devono essere sia quasi statiche che senza attriti.
Queste trasformazioni meravigliose, assolutamente immaginarie, sono denominate, come si è visto,
trasformazioni reversibili. Il loro nome sta a significare che esse possono essere seguite da un
sistema termodinamico in entrambe le direzioni temporali, sia in avanti che indietro. Infatti,
eliminati tutti gli effetti dissipativi irreversibili, non c’è motivo per cui, a partire dalla fine, il
sistema non possa ripercorrere i suoi passi e tornare al punto di partenza. Se non ha perso nulla per
strada ed è passato solo attraverso stati di equilibrio allora non vi sono impedimenti a che ciò
avvenga. Ad esempio una espansione isoterma reversibile, quella che conosciamo benissimo ed ha
equazione PV=costante, può tranquillamente diventare una compressione isoterma reversibile senza
scomporsi minimamente. Vale a dire: prima il gas si espande, poi si ricontrae, e nell’Universo, alla
fine, non rimane traccia alcuna di quello che è successo al gas.
Per usare una immagine familiare: se guardiamo il filmato, ad esempio, di un pallone che rimbalza,
nella realtà non avremmo dubbi sul fatto se il filmato stia scorrendo in avanti oppure indietro.
Difatti ad ogni rimbalzo si disperde un poco di energia sotto forma di calore e la risalita è un poco
più bassa ogni volta, finché, da ultimo, tutto il calore si è dissipato per attrito, la palla si è riscaldata,
in perfetto accordo con il primo principio, e giace sconsolata a terra. Ma se, per caso, vivessimo in
un mondo dove tutte le trasformazioni fossero reversibili, non avremmo attriti e le cose andrebbero
diversamente. Gi attriti di cui si parla nell’esempio descritto sono le molecole dell’aria dentro alla
palla, le quali, quando questa si comprime e si dilata durante il rimbalzo, si strofinano
(interagiscono elettricamente, per dirla bene) e si riscaldano (acquistano energia cinetica a livello
microscopico). In questo mondo immaginario, dopo ogni rimbalzo la palla risalirebbe sempre alla
stessa altezza e non si riscalderebbe di certo. Davvero saremmo in difficoltà nello stabilire se il film
stia scorrendo in avanti oppure indietro. In questo senso il fenomeno in esame sarebbe del tutto
reversibile. Queste riflessioni ci condurranno, come vedremo, a collegare lo scorrere del tempo solo
all’esistenza di fenomeni irreversibili.
Ma si consideri anche che nessuna delle trasformazioni termodinamiche reali nelle quali avviene
uno scambio di calore può essere reversibile. Difatti lo scambio di calore è un processo turbolento
che consegue ad una differenza di temperatura, ed è quindi impossibile per definizione individuare
un solo valore di T nel complesso di oggetti coinvolti.
Le trasformazioni reversibili comportano, quindi, la situazione irreale di uno scambio di calore
senza che ci sia differenza di temperatura, e pertanto senza che ci siano gli attriti delle turbolenze.
In via teorica si può immaginare che il passaggio reversibile di calore avvenga fra due corpi la cui
temperatura differisca per valori piccolissimi, ma si tratta di una via ideale difficilmente praticabile.
UNA TRASFORMAZIONE REVERSIBILE È QUASI STATICA E SENZA DISSIPAZIONI E PERTANTO:
1. COMPORTA SCAMBI DI CALORE SENZA DIFFERENZE DI TEMPERATURA
2. HA UGUALE PROBABILITÀ DI AVVENIRE NELLE DUE DIREZIONI TEMPORALI
3. IL SUO PROCEDERE SI PUÒ INVERTIRE (OPPURE ARRESTARE) CON PICCOLISSIME
MODIFICHE DELLE VARIABILI TERMODINAMICHE RISPETTO AI VALORI COINVOLTI
PERCORSA IN AVANTI E POI INDIETRO NON LASCIA TRACCE NELL’AMBIENTE
4.
5. SI PUÒ RAPPRESENTARE CON UN GRAFICO ESSENDO SEMPRE DEFINIBILI P E T
Torniamo al motore di Carnot: in esso ci sono quindi trasformazioni solo reversibili: si può andare
avanti ed indietro con eguale probabilità e senza modificare l’ambiente in modo permanente. Basta
questo a fare di esso il miglior motore del mondo? Non proprio. Kelvin e Clausius ci hanno detto
che non si può fare a meno di cedere calore, oltre che riceverlo, se vogliamo un motore che
funzioni. In particolare per Kelvin il motore che scambia calore con una sorgente sola non può
funzionare. E allora, dice Carnot, facciamo la cosa più semplice possibile dopo il motore –
impossibile - ad una sola sorgente. Cosa? Il motore che scambia calore con due sole sorgenti,
ovviamente. Due e non più di due.
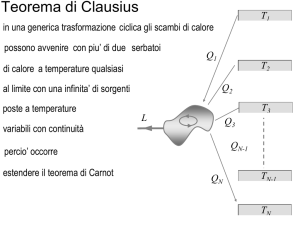
Guardiamo la figura di prima, quella con i tre cicli compresi fra le due isoterme di temperatura
massima e minima. Si tratta di cicli che seguono trasformazioni reversibili, dato che sono
rappresentati da delle linee. Se non fossero reversibili nemmeno potrei rappresentarle sul piano P,
V. Ecco una domanda per voi: quante isoterme ci sono fra quella massima e quella minima? Una?
Due? Cinque? Nooo, molte di più. In teoria ce ne stanno infinite. Stiamo parlando di numeri reali,
attenzione. Supponiamo che l’ isoterma a temperatura minima sia a 300 K e quella massima a 400
K. Chiedersi quante isoterme ci sono fra la massima e la minima è un po’ come chiedersi: quanti
numeri reali ci sono fra 300 e 400 ? Ci sono infiniti numeri, e quindi infinite isoterme. Non solo.
Dato che i cicli indicati in figura non seguono trasformazioni senza scambi di calore, cioè non
seguono trasformazioni adiabatiche, il sistema deve scambiare calore durante tutto il tragitto del
ciclo e deve scambiarlo mentre varia la sua temperatura. E se vogliamo che gli scambi di calore
siano reversibili anche la temperatura della sorgente con cui il sistema interagisce deve variare,
perché, lo si è visto, uno scambio di calore fra oggetti a temperatura diversa comporta
irreversibilità.Il sistema deve scambiare calore, quindi, con infinite sorgenti tutte a temperatura
diversa.
Ma come è possibile questo? Infinite sorgenti? Anche qui va ricordato che è tutto teorico. Noi con il
termine sorgente di calore intendiamo una astrazione, un sistema immaginario la cui temperatura si
mantiene uniforme e costante nonostante gli scambi di calore, e che scambia energia solo attraverso
flusso di calore (niente esecuzione di lavoro). In molte applicazioni, il terreno, l’aria atmosferica,
l’acqua di un fiume o del mare possono essere assimilati a sorgenti.
In un ipotetico ciclo reversibile gli scambi di calore tra sistema evolvente e sorgenti avverrebbero
senza differenze di temperatura tra sistema e sorgenti: è quindi indifferente, se ci riferisce a cicli
reversibili, parlare di temperatura del sistema piuttosto che di temperatura della sorgente con cui il
sistema scambia calore. Le infinite sorgenti possono essere pensate come una sorgente a contatto
col sistema che cambia anche essa temperatura durante le trasformazioni. Ma lasciamo da parte le
infinite sorgenti: senza esagerare si può pensare a qualcosa di più semplice: motori che scambiano
calore con tre, quattro sorgenti. Il ciclo di Carnot semplifica al massimo: il motore più semplice
deve scambiare calore con due sole sorgenti, una calda ed una fredda.
Ma come dovrà essere fatto un tale motore? In primo luogo, avrà una fase in cui produce lavoro
ricevendo calore dalla sorgente calda, a temperatura TC . In tale fase, la sostanza sfruttata
all’interno del motore deve quindi dilatarsi termicamente e, al tempo stesso, rimanere a temperatura
costante. Se infatti la temperatura variasse, dovendo essere il sistema in equilibrio con la sorgente,
dovrei cambiare la temperatura della sorgente stessa e quindi avrei una terza sorgente con la quale il
sistema scambierebbe calore, mentre voglio solo due sorgenti in tutto. Questa fase, di assorbimento
di calore e generazione di lavoro a temperatura costante deve pertanto essere una espansione
isoterma.
Successivamente il sistema va raffreddato fino alla temperatura TF della sorgente fredda . L’unico
modo per passare da TC a TF senza che avvengano scambi di calore, il che richiederebbe altre
sorgenti a temperature intermedie, è attraverso una espansione adiabatica.
Adesso che il sistema è alla temperatura TF devo ricomprimerlo per riportarlo al volume iniziale.
Valgono le considerazioni fatte sopra: compio del lavoro per ridurre il volume mantenendo il
sistema a temperatura costante, la trasformazione è ancora una isoterma.
Da ultimo, affinché il sistema si trovi esattamente nelle condizioni di partenza, è necessario
riportarlo alla temperatura TC senza ulteriori scambi di calore, altrimenti occorrerebbero delle
sorgenti intermedie ulteriori. Questo è possibile tramite una compressione adiabatica.
IL
CICLO DI CARNOT È DUNQUE UN CICLO MOTORE REVERSIBILE A DUE SOLE SORGENTI,
COSTITUITO DA DUE ISOTERME E DUE ADIABATICHE, QUESTO QUALUNQUE SIA LA NATURA DEL
SISTEMA FISICO CHE SUBISCE IL CICLO.
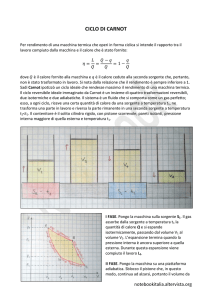
Allo scopo di calcolare il suo rendimento, possiamo supporre che si tratti di un gas perfetto e
rappresentare quindi il ciclo come si è fatto in figu r a 3 . 1 . A partire dallo stato di equilibrio 1, il gas
si espande in modo reversibile, dapprima a temperatura costante fino allo stato 2, poi
adiabaticamente fino allo stato 3; dopo di che viene compresso in modo reversibile, prima a temperatura costante fino allo stato 4, poi senza
scambio di calore fino allo stato iniziale 1.
p
Durante l’espansione 1 2 viene fornito al gas,
1
da parte di una sorgente calda a temperatura TC ,
il calore necessario a mantenerne costante la
temperatura nonostante l’espansione. Trattandosi
2
di un gas perfetto, anche l’energia interna rimane
costante, cioè U  0 . Quindi, applicando il
primo principio, si ha che il calore QC assorbito
4
dal gas viene utilizzato tutto nell’esecuzione di
3
lavoro:
V
Q C = W12 = n RTC log 2
V1
V
Figura 3.1 Il motore di Carnot
Durante la fase 23 non c’è scambio di calore, e
il gas compie un lavoro esterno positivo W 23
che viene «pagato » con una corrispondente diminuzione dell’energia interna (il gas quindi si
raffredda).
Durante la fase 3 4 viene sottratto al gas, da parte di una sorgente fredda a temperatura TF , calore
affinché, nonostante la compressione, non si riscaldi: l’energia interna resta costante, e al gas viene
sottratto un calore Q F pari (in valore assoluto) al lavoro W 3 4 (negativo) che esso compie:
V
V
|Q F |= |W3  4 |  | n RTF log 4 | nRTF log 3 .
V3
V4
essendo infatti
V4
V
V
V
V
 1 risulta log 4  0 , da cui: log 4   log 4  log 3
V3
V3
V3
V3
V4
Infine, durante la fase 41 il gas, compresso senza sottrazione di calore, si riscalda fino alla
temperatura iniziale, con un aumento di energia interna pari al valore assoluto del lavoro resistente
compiuto.
In definitiva, il gas assorbe calore ad alta temperatura e ne restituisce una parte a bassa temperatura:
la differenza tra calore scambiato in entrata e calore scambiato in uscita determina il lavoro
compiuto: Q C – | Q F |= W.
Se ci riferiamo al caso particolare di un gas perfetto, è immediato trovare che in un ciclo di Carnot il
rapporto tra il calore scambiato in uscita e il calore scambiato in entrata è uguale al rapporto tra le
|Q | T
rispettive temperature di scambio: F  F . Infatti risulta:
QC
TC
V
nRTF ln 3
| QF | | W34 |
V4
.


V
QC
W12
nRTC ln 2
V1
Ma nella trasformazione adiabatica 23 risulta TC V2 1 = TF V3 1 , e nella trasformazione adiabatica
41 risulta TC V1 1  TF V4 1 . Dividendo membro a membro le equazioni delle due adiabatiche si
trova V2 /V1 = V3 /V4 .
Sostituendo questa relazione in quella che dà il rapporto fra i calori scambiati si semplificano i due
logaritmi a numeratore e denominatore. Il modulo si elimina dato che le quantità rimaste sono
| QF | TF
sicuramente positive, ed il risultato finale è quello anticipato:
. Ne deriva che, nel caso

QC
TC
T
di un gas perfetto, il rendimento di un ciclo di Carnot è  c = 1  F .
TC
Abbiamo quindi dimostrato che quando un gas perfetto subisce un ciclo di Carnot il rendimento del
ciclo dipende solo dalla temperatura delle due sorgenti: non dalla particolare posizione, nel piano di
Clapeyron, dei vertici del ciclo sulle due isoterme.
MA SOPRATTUTTO NOTIAMO CHE NEMMENO UN MOTORE PERFETTO, REVERSIBILE, E A DUE SOLE
SORGENTI, TRASFORMA TUTTO IL CALORE IN LAVORO.
Perché il suo rendimento sia elevato, occorre che la temperatura TF della sorgente fredda sia
piccola in rapporto alla temperatura TC della sorgente calda. Se la temperatura Kelvin della sorgente
fredda fosse zero, il rendimento risulterebbe unitario: tutto il calore assorbito dalla sorgente calda
verrebbe trasformato in lavoro. Ma, come abbiamo già fatto notare, questa possibilità è negata dal
secondo principio della termodinamica.
Per lo stesso motivo non è possibile ipotizzare che la sorgente fredda possa trovarsi a una
temperatura Kelvin minore di zero: in tal caso risulterebbe negativo anche il calore scambiato in
uscita, il che significa che il sistema scambierebbe calore solo in entrata (a due diverse temperature)
e, in contrasto col secondo principio, lo convertirebbe integralmente in lavoro.