Esercizio 1

Programmazione Lineare
La ricerca operativa mira a risolvere i problemi di ottimizzazione attraverso
l’implementazioni di programmi, cioè, di algoritmi.
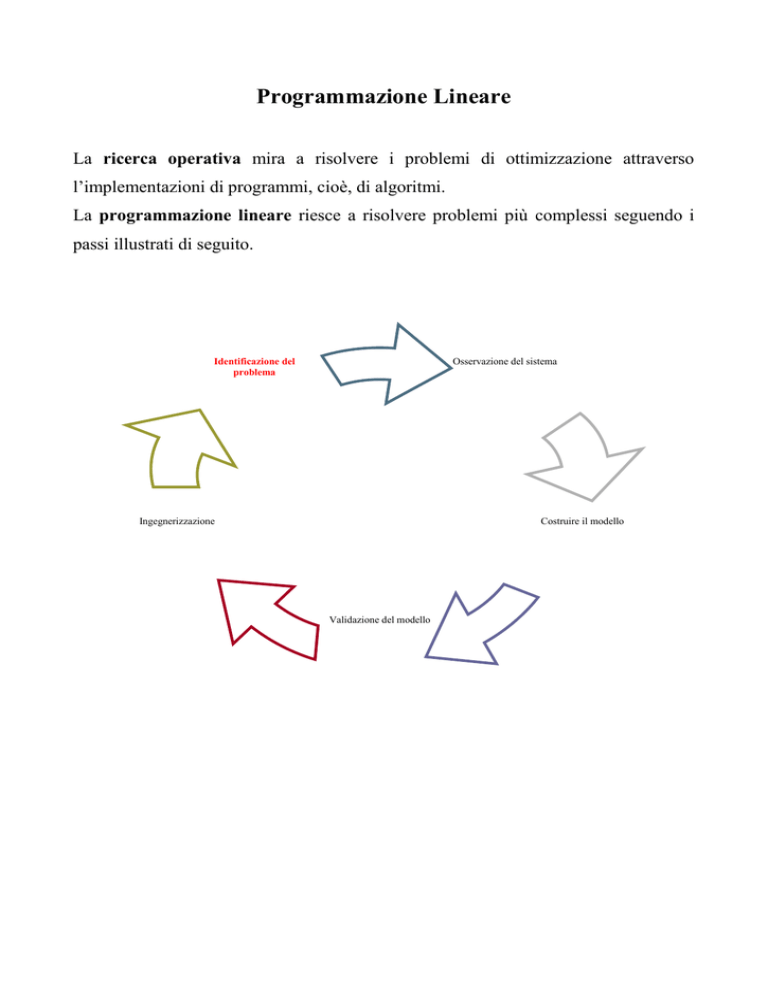
La programmazione lineare riesce a risolvere problemi più complessi seguendo i
passi illustrati di seguito.
Identificazione del
problema
Osservazione del sistema
Ingegnerizzazione
Costruire il modello
Validazione del modello
Un problema affinché possa essere risolto deve essere posto nel modo seguente:
min z  x 

 Ax  b
 x0

funz.obiettivo
funz.lineare
- f : Rn  Rn
Le proprietà di linearità sono:
- proprietà additiva f x  y   f x  f  y  x, y  R n
- proprietà di proporzionalità f x  f x x  R n ,   R
-
x : variabili decisionali, viene rappresentato attraverso un vettore di n
dimensione.
 x1 
x 
x   2
 ... 
 
 xn 
x  Rn
- A è la matrice dei coefficienti di vincolo così definita:
A  R mn
 b1 
b 
b   2
 ... 
 
bn 
- b  Rm
n
- z  x    ci  xi ,
i 1
 c1 
c 
ci sono i coefficienti di costo: c   2 
 ... 
 
c n 
- z x   c T  x
In sintesi il problema diventa:
min z x 

 a x  a x  ...  a x  b
12 2
1n n
1
 11 1

...
a x  a x  ...  a x  b
m2 2
mn n
m
 m1 1

x1  0, x 2  0,..., x n  0
Esempio
Formulazione di un problema di PL: Modello di Produzione
Un industria chimica produce tre tipi di composti A, B, C, utilizzando per la
produzione due stabilimenti. Nel primo, un’ora di lavorazione costa 50 euro e
vengono prodotti 3 Kg di composto A, 2 Kg di composto B e 3 Kg di composto
C.
Nel secondo impianto, dove un’ora di produzione ha un costo pari a 75 euro, ogni
ora si producono 4 Kg di composto chimico A, 4 Kg di composto chimico B e 5
Kg di composto C. Dei tre composti chimici è richiesta una produzione giornaliera
pari ad almeno 90, 120 e 100 Kg rispettivamente.
La produzione dei tre composti comporta la generazione di sostanze inquinanti; in
particolare per ogni Kg di composto A si producono 20 gr di sostanza inquinante,
mentre per ogni Kg di composto B o C la quantità di sostanza inquinante prodotta
è pari a 10 gr. Una legge regionale sul controllo della qualità dell’ambiente
impone che non è possibile produrre giornalmente più di 5 Kg di sostanze
inquinanti.
Considerando che ogni impianto può essere utilizzato a ciclo continuo, formulare
il modello di programmazione lineare relativo alla pianificazione ottimale della
produzione giornaliera dei tre composti chimici, con l’obiettivo di minimizzare i
costi complessivi di lavorazione.
- x1  n° di ore di lavorazione dell’impianto 1
- x2  n° di ore di lavorazione dell’impianto 2
- zx  50x1  75x2 ,
50 e 75 sono coefficienti di costo
Vincoli sulla produzione, cioè sulla quantità da produrre
 3x1  4 x2  90  prodottoA

2 x1  4 x2  120  prodottoB
3x  5 x  100  prodottoC 
2
 1
Vincoli sull’utilizzo degli stabilimenti
Ogni impianto può essere utilizzato a ciclo continuo:
 x1  24

 x2  24
Vincoli sulla quantità di sostanza inquinante
3Kg  20 gr  2 Kg  10 gr  3Kg  10 gr  110 gr
4 Kg  20 gr  4 Kg  10 gr  5Kg  10 gr  170 gr
110x1  170x2  5000
Programmazione Lineare in forma standar:
min z  x 

 z  x   50 x  75 x
1
2

sistema  di  vincolo :

3 x1  4 x 2  90

 2 x1  4 x 2  120

 3 x1  5 x 2  100
 110 x1  170 x 2  5000

x1  24


x 2  24

x1  0; x 2  0

1IMPIANTO
2IMPIANTO
4 
 3
 2
4 

 3
5 
A
;
110
170


 1
0 


1 
 0
x 
x   1 ;
 x2 
 90 
 120 


 100 
b
.
5000


 24 


 24 
Le condizioni standard impongono di avere uguaglianze e non
disuguaglianze. Quindi se ci troviamo nel caso in cui:
max z x   min z x 




max f x  : x  R n   min f x  : x  R n
f  x    f x 
z x   3x1  4 x 2  5 x3  max z x 
z x    z x   3 x1  4 x 2  5 x3  min z  x 
Vincoli espressi con disuguaglianze:
-
a
ij
 x j  bj
Si introduce a questo punto la variabile ausiliaria si  bi   aij  x j che per
essere introdotta nella programmazione lineare deve essere si  0 .
110x1  170x2  5000 introduciamo x3 e diventa:
110 x1  170 x2  x3  5000
-
a
ij
 x j  bj
Introduciamo anche questa volta una variabile ausiliaria:
si   aij  x j  bi
si  0
3x1  4 x 2  90  x 4
3x1  4 x 2  x 4  90
- Quando una delle variabili decisionali non è x  0 si introducono altre
variabili decisionali:
x j , x j
xj  0  
x j  0, x j  0
x j  x j  x j
x j  x j  0
Ritornando all’esercizio, ci occorrono le seguenti variabili ausiliari:
x3 , x4 , x5 , x6 , x7 , x8
L’esposizione del problema in questione diventa:
 3x1  4 x 2  x3  90
 2 x  4 x  x  120
1
2
4

 3x1  5 x 2  x5  100

110 x1  170 x 2  x6  5000

x1  x7  24


x 2  x8  24
 90 
 120 


 100 
b
;
5000 
 24 


 24 
4 1 0 0 0 0 0 
 3
 2
4
0  1 0 0 0 0 

 3
5
0 0 1 0 0 0 
A
.
110 170 0 0 0  1 0 0 
 1
0
0 0 0 0 1 0 


1
0 0 0 0 0  1
 0
 m  n Si hanno più equazioni di vincolo rispetto alle incognite;
 m  n Il numero di equazioni è uguale alle incognite, è risolvibile
quando:
1. det A  0
2. det A  0
Nel caso (1) esiste una soluzione; nel caso (2) è possibile che ci sia un’equazione
ridondante
 m  n Esistono infinite soluzioni. Risulta un problema trovare quella ottima e
affinché il problema venga risolto si deve verificare che:
 p  A  m
 Il problema risulta ben posto.

 mn
- Verificare se in A ci sono delle colonne linearmente indipendenti, quindi se è
possibile estrarre una matrice.
- Ci sono infinite soluzioni che verificano i vincoli
Se
m3
n5
n!
1  2  3  4  5 120


 10
m!n  m!
62
12
10 sono le soluzioni di base, all’interno delle quali c’è la soluzione ottima.
Come si calcolano le soluzioni di base?
- s  s1 , s2 ,..., sm  è l’insieme degli indici di base
- A  R mn
1 2 3  n 
 




A








Se le colonne 1,2 e 5 sono linearmente indipendenti allora avremo che:
1 2 5






As  
,
  






1 2 7 






As  
,
  






Può succedere che si hanno più colonne linearmente indipendenti e quindi
possiamo estrarre più matrici. Quindi si avranno più insiemi s per quante
sottomatrici di A esistono.
 x1   x1 
   
   
x     x m ;
   
   
 x n   x n 
 x1 
 
 
Variabili di base: x s    ;
 
 
 x m 
 x m 1 



Variabili non di base: xG    



 x n 
La stessa cosa possiamo fare per la matrice A:

A   As


AG 

Il problema in forma standard diventa:
min z x 


 xs 
 z x   c T  x  C s C G  

 xG 
S
.
V
.


 xs 
As AG    b  Ax  b
 xG 


x s  0, xG  0
As  x s  AG  xG  b
As è costituita da colonne linearmente indipendenti, non è singolare ma essendo
quadrata è invertibile.
As1  As  x s  As1  AG  xG  As1  b
x s  As1  AG  xG  As1  b
ponendo  xG  0
x s  As1  b
Infine una soluzione di base è ammissibile quando soddisfa i vincoli.
Esempio 1
 2 x1  2 x 2  x3  x 4  10
2 x  x  x  2 x  x  12
 1
2
3
4
5

4
x

x

2
x

3
x
1
2
3
4 8


x1 , x 2 , x3 , x 4 , x5  0
- Si definisce di seguito la matrice A 3 5 :
1
2
3
4
5
 2 2 1 1 0
A  2 1 1 2 1
4 1 2 3 0
-
n!
1 2  3  4  5

 10 soluzioni base
m!n  m ! 1  2  32
- Il vettore dei termini noti:
10
b  12
 8 
Consideriamo a caso un insieme a caso di indici di base:
 2 1 0
s  2,3,5  As  1 1 1 , dato che risulta il det As  3  0 allora si può dire che le tre
1 2 0
colonne sono linearmente indipendenti e quindi a queste ultime è associata una
soluzione di base.
- La soluzione di base è fatta nel seguente modo:
0
x 
 2
s  x 2 , x3 , x5   2,3,5  x s   x3 
 
0
 x5 
 x1  0
 x4  0
Si pone: 
Allora il sistema diventa il seguente:
 2 x 2  x3  10
 x2  4


 x 2  x3  x5  12   x3  2
 x  2x  8
x  6
3
 5
 2
Infine il vettore delle soluzione è di seguito riportato:
0 
4
 
x  2
 
0 
6
E’ una soluzione ammissibile perché verifica i vincoli e le condizioni. Questa
rappresenta una delle 10 soluzioni che siamo in grado di calcolare.
Esempio 2
Ad esempio se:
 0 
 0 


s  3,4,5  x   22 


 12
 14 
Rappresenta una soluzione di base non ammissibile a causa del valore negativo.
Una volta che si sono calcolate tutte le 10 soluzioni di base il problema si risolve
con la ricerca della soluzione ottima che è quella che minimizza la funzione
obiettivo. ( Tutto ciò può essere calcolato automaticamente con un programma di
calcolo che utilizza l’algoritmo del simplesso?).
Interpretazione geometrica della Programmazione Lineare
 Definizione di Combinazione convessa:
1
2 
k 
x , x , x  con : x
0    1,    1
i 
 Rn
k
i
i
i
x  1  x 1  2  x 2     k  x k   vettore  risul tan te
x  Rn
sono vettori
x
i
x spazio Euclideo di n dimensione
Se tutte le combinazioni sono verificate il vettore risultante è definito
combinazione commessa.
 Definizione di Insieme convesso:
  R n convesso 
x 1 , x 2  ,, x k   
k
0  xi  1,  i  1
i
x  1 x
1
 2 x 2     k x k   
E’ combinazione convessa
 Definizione di Insieme delle soluzioni ammissibili

 x  R

 i  x  R n : ai x  bi sistema di vincoli che devono soddisfare le variabili
j
n

: xj  0
  i   j insieme di soluzioni ammissibili
 Punto Estremo:
x 
 x 1 , x 2  ,, x k   
0  i  1,
k

i
1
i
x  1 x 1    k x k   
Esempio
Quali sono le fasi che ci permettono di trovare la soluzione ottima?
1. Individuare  ;
2. Verificare che   0 e cioè che non sia un insieme vuoto;
3. Individuare i punti estremi di 
4. Ricavare la soluzione ottima
 min z  x 
 z x   x  2 x
1
2


S .V .

 x1  2 x 2  10
 x  x 1
2
 1
x2  4


 x1 , x 2  0
Ad ognuno dei tre vincoli posso associare una retta:
I Vincolo: x1  2x2  10
r1 : x1  2x2  10
II Vincolo: x1  x2  1
r2 : x1  x2  1
III Vincolo: x2  4
r3 : x2  4
X2
Insieme 
5
4
E
D
r3
r1
A
C
1
X1
r1
1
10
B
Il problema illustrato è un problema di minimo.
A, B, C, D, E rappresentano i punti estremi di  .
A  0,1;
B  1,0;
C  10,0;
E  0,4
D invece si deve calcolare, considerandolo come intersezione di r1 e r3 .
x  2
D 1
 x2  4
zx  x1  2x2
Avremo che:
zA  2
zB  1
z C  10
z D  10
zE  8
Siccome in questo caso stiamo studiando un problema di minimo, B è la nostra
soluzione ottima.
Questo concetto può essere dimostrato per via grafica se si tiene presente c i
coefficienti che compaiono nella funzione obiettivo zx  x1  2x2  ;
1 
c 
 2
c è un vettore gradiente e se rappresentato nel piano risulta facile intuire la
soluzione
x2
2
x1
1
Se il problema fosse stato di massimizzazione il verso del gradiente sarebbe stato
l’opposto e avrebbe dato infinite soluzioni ottime:
C  z c  10
D  z D  10
Questo perché le rette perpendicolari al vettore gradiente, risultano essere parallele a
r1, perciò risulta che tutti i punti su r1 sono soluzioni ottime.