Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
Soluzioni degli esercizi di riepilogo
d
d
QGianni
Q Emilia
Q
0
d
4,
il
4,
di
se P €4
se P €4
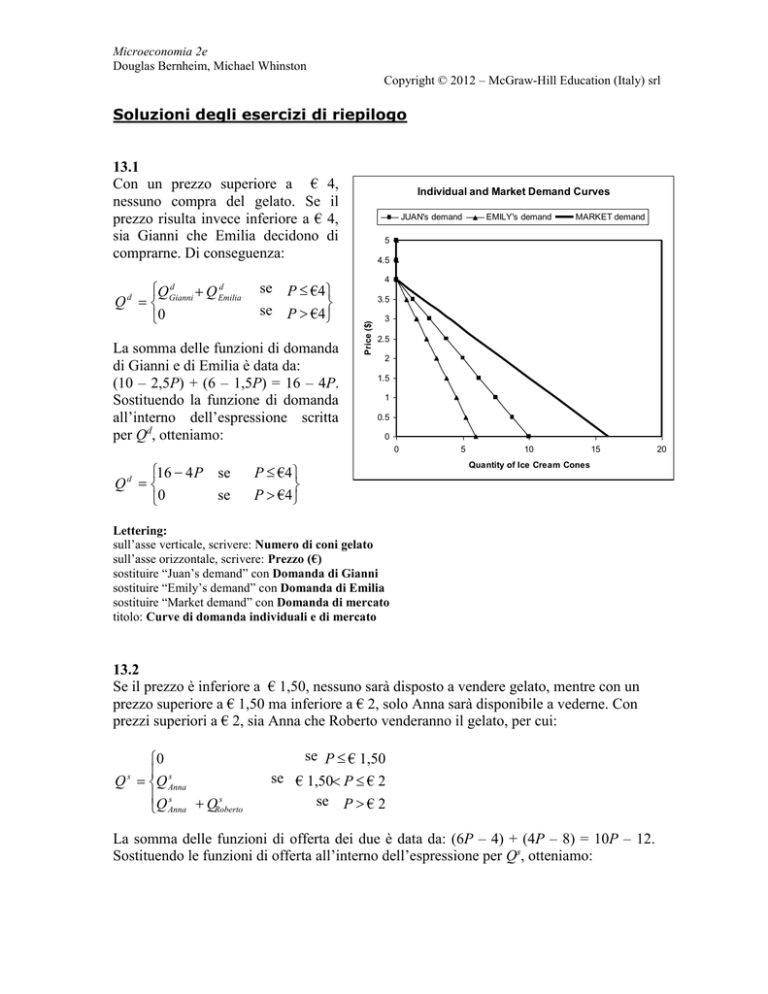
La somma delle funzioni di domanda
di Gianni e di Emilia è data da:
(10 – 2,5P) + (6 – 1,5P) = 16 – 4P.
Sostituendo la funzione di domanda
all’interno dell’espressione scritta
per Qd, otteniamo:
Individual and Market Demand Curves
JUAN's demand
MARKET demand
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
0
16 4 P se
Qd
se
0
EMILY's demand
5
Price ($)
13.1
Con un prezzo superiore a €
nessuno compra del gelato. Se
prezzo risulta invece inferiore a €
sia Gianni che Emilia decidono
comprarne. Di conseguenza:
P €4
P €4
5
10
15
Quantity of Ice Cream Cones
Lettering:
sull’asse verticale, scrivere: Numero di coni gelato
sull’asse orizzontale, scrivere: Prezzo (€)
sostituire “Juan’s demand” con Domanda di Gianni
sostituire “Emily’s demand” con Domanda di Emilia
sostituire “Market demand” con Domanda di mercato
titolo: Curve di domanda individuali e di mercato
13.2
Se il prezzo è inferiore a € 1,50, nessuno sarà disposto a vendere gelato, mentre con un
prezzo superiore a € 1,50 ma inferiore a € 2, solo Anna sarà disponibile a vederne. Con
prezzi superiori a € 2, sia Anna che Roberto venderanno il gelato, per cui:
0
s
s
Q Q Anna
s
Q s
Anna QRoberto
se P € 1,50
se € 1,50 P € 2
se P € 2
La somma delle funzioni di offerta dei due è data da: (6P – 4) + (4P – 8) = 10P – 12.
Sostituendo le funzioni di offerta all’interno dell’espressione per Qs, otteniamo:
20
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
0
s
Q 6 P 4
10 P 12
P €1,50
se €1,50 P €2
se P €2
se
Nel disegnare il grafico di tali funzioni, occorre prestare attenzione soprattutto alla curva
di offerta di Anna: tale curva non deve toccare l’asse in cui sono riportati i prezzi, dato
che Anna produce 5 unità quando il prezzo è di € 1,50 e non produce nulla se il prezzo è
sotto tale soglia.
Individual and Market Supply Curves for Ice
Cream
ANITRA's Supply Curve
ROBERT's Supply Curve
MARKET Supply Curve
3
2.5
Price ($)
2
1.5
1
0.5
0
0
5
10
15
20
Quantity of Ice Cream Cones
Lettering:
sull’asse verticale, scrivere: Numero di coni gelato
sull’asse orizzontale, scrivere: Prezzo (€)
sostituire “Anitra’s supply curve” con Curva di offerta di Anna
sostituire “Robert’s supply curve” con Curva di offerta di Roberto
sostituire “Market supply curve” con Curva di offerta di mercato
titolo: Curve di offerta individuali e di mercato
13.3
Cerchiamo innanzitutto di individuare il punto di minimo della funzione dei costi medi
(data dal costo totale C(Q) diviso per la quantità Q): AC = 4 + Q/40. Si vede chiaramente
come il valore minimo di tale funzione sia 4. Per ottimizzare la scelta di produzione,
imponiamo P = MC. Sostituendo all’interno dell’espressione data nel problema per il
costo marginale MC, otteniamo P = 4 + (Q/20). La curva di offerta è quindi:
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
20 P 80 se
Qs
se
0
P €4
P €4
Se vi sono 10 imprese operanti su questo mercato, l’offerta aggregata risulterà:
10 20 P 80 200 P 800 se
Qs
se
10 0 0
P €4
P €4
Se ve ne fossero 20, la curva di offerta risulterebbe invece:
20 20 P 80 400 P 1,600 se
Qs
se
20 0 0
P €4
P €4
Sotto l’ipotesi di libero ingrasso sul mercato, ogni impresa deve produrre secondo la scala
di produzione efficiente. Sotto tale ipotesi, pertanto, l’offerta di mercato sarà
rappresentata da una retta perfettamente orizzontale in corrispondenza di P = € 4.
13.4
I panifici con bassi costi di produzione decideranno di essere attivi sul mercato in
corrispondenza di ogni livello di prezzo superiore a quello che rende Qs uguale a zero,
che corrisponde ad un prezzo di € 0,50. I panifici con elevati costi di produzione
decideranno invece di essere operativi solo a fronte di prezzi € 1,00. Se il prezzo fosse
quindi di € 0,75, solo i panifici con costi di produzione più bassi risulterebbero attivi.
Sappiamo che, a questo livello di prezzo, ognuno di questi panifici produrrà 200(0,75) –
100 = 50 pagnotte. Dal momento che questi panifici sono 9, l’offerta complessiva
ammonterà a 500 pagnotte.
Se il prezzo del pane salisse a € 1,25, tutti i panifici diventerebbero operativi e l’offerta
di mercato sarebbe data dalla somma della quantità prodotta dai panifici con bassi costi di
produzione e da quella prodotta dai panifici con elevati costi di produzione:
[200(1,25) – 100] + [200(1,25) – 200] = 150 + 50 = 200.
La curva di offerta di mercato di breve periodo risulta pertanto:
se P € 0,50
0
s
Q Qbassicos ti
se € 0,50 P € 1
s
Q s
se P € 1
bassicos ti Qalticos ti
s
La somma delle funzioni di offerta delle due tipologie di panifici è data da : (200P – 100)
+ (200P – 200) = 400P – 300.
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
Short-Run and Long-Run Market Supply
se P € 0,50
0
s
Q 200 P 100 se € 0,50 P € 1
400 P 300
se P € 1
SHORT RUN
LONG RUN
2
1.75
1.5
1.25
Price ($)
Non vi sono informazioni sufficienti per
discutere quanto possa avvenire nel lungo
periodo, a meno che non si assuma che il
prezzo originario di € 0,75 rappresenti il
prezzo di equilibrio di lungo periodo. In tal
caso, nel lungo periodo ci aspettiamo che il
prezzo torni a questo livello, facendo sì che la
curva di offerta di mercato torni ad essere una
curva
perfettamente
orizzontale
in
corrispondenza di P = € 0,75.
1
0.75
0.5
0.25
0
0
100
200
300
400
Quantity Supplied
Lettering:
sull’asse verticale, scrivere: Quantità offerta
sull’asse orizzontale, scrivere: Prezzo (€)
sostituire “Short run” con Breve periodo
sostituire “Long run” con Lungo periodo
Titolo: Offerta di mercato di breve e lungo periodo
13.5
La curva di offerta di lungo periodo (ipotizzando piena libertà di entrata sul mercato) è
data da una linea orizzontale in corrispondenza del minimo del costo medio, che può
essere individuato imponendo l’uguaglianza fra costi medi e costi marginali. Per prima
cosa ricaviamo AC, che è dato da C(Q) diviso per Q (comprendendo nel costo totale
anche i costi fissi).
AC = 4 + Q/40 + 10/Q.
MC = AC
Q
Q 10
4
4
20
40 Q
Q 10
40 Q
Q2 = 400
Q = 20
Il valore di minimo di AC viene raggiunto quando Q = 20. Sostituendo tale valore
all’interno della funzione AC (o MC), scopriamo come il valore di minimo sia pari a € 5.
500
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
L’offerta di mercato di lungo periodo è quindi rappresentata da una linea orizzontale in
corrispondenza di P = € 5.
13.6
Dall’Esercizio 13.1, sappiamo che la domanda di mercato è data da:
16 4 P se
Qd
se
0
P€ 4
P€ 4
Dall’Esercizio 13.2, sappiamo invece che l’offerta di mercato è data da:
0
s
Q 6 P 4
10 P 12
se P € 1,50
se €1,50 P € 2
se P € 2
Uguagliamo la quantità offerta con quella domandata, assumendo che il prezzo sia
sufficientemente alto per cui entrambi i produttori sono attivi sul mercato, ma allo stesso
sufficientemente contenuto per far sì che entrambi i consumatori vogliano acquistare:
Qd = Qs
16 – 4P = 10P – 12
28 = 14P
P=€2
Tale soluzione è accettabile visto che € 2 è un prezzo sufficientemente basso da indurre
entrambi i consumatori a domandare del gelato ma anche sufficientemente alto per
indurre entrambi i produttori a operare sul mercato. Inserendo un prezzo di € 2 nella
funzione di domanda (o di offerta), troviamo che la quantità di equilibrio è pari a:
16 – 4(2) = 10(2) – 12 = 8.
In equilibrio, il prezzo è di € 2 e la quantità scambiata corrisponde a 8 coni gelato.
13.7
Il costo medio è la somma del costo fisso e del costo variabile, il tutto diviso per Q:
CF CV
Q
50 Q
AC =
Q 2
AC =
Nell’equilibrio di breve periodo, sappiamo che MC = AC, e da questa condizione si
deriva la scala di produzione efficiente per ciascuna impresa:
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
MC = AC
50 Q
Q
Q 2
Q 50
2 Q
Q2 = 100
Q = 10
Sostituendo tale quantità all’interna della funzione per AC o MC, individuiamo il valore
di minimo del costo medio, che corrisponde a € 10. Questo è dunque il prezzo di
equilibrio nel breve periodo; a tale prezzo, ogni impresa produce 10 pizze. Per calcolare il
numero totale di pizze vendute e consumate, utilizziamo la funzione di domanda: Qd =
750 – 25(10) = 500. Siccome ciascuna impresa produce 10 pizze, vi saranno 50 imprese
operanti sul mercato per soddisfare la domanda complessiva.
Se i costi marginali MC dovessero crescere nel breve periodo, diventando MC = Q +6,
per soddisfare la condizione P = MC, le imprese dovrebbero modificare la loro offerta:
P = MC
P=Q+6
Q=P–6
Questa è la curva di offerta di breve periodo per ogni impresa presente sul mercato, dopo
la variazione dei costi marginali.
Nel breve periodo, i prezzi devono essere maggiori del valore di minimo del costo medio
variabile. Se il costo marginale aumenta di € 6, il costo variabile aumenta di 6Q; la nuova
funzione dei costi variabili è ora: Q2/2 + 6Q.
Ne deriva che il costo variabile medio è ora: Q/2 + 6.
Il minimo di tale funzione è, ovviamente, rappresentato da 6 (valore raggiunto quando Q
=0); la curva di offerta sopra descritta è valida solo per prezzi superiori a € 6. Siccome vi
sono 50 imprese, identiche fra loro, operanti sul mercato, l’offerta di mercato risulta
allora:
50 P 6 50P 300 se P € 6
Qs
se P € 6
50 0 0
Uguagliamo offerta e domanda di breve periodo:
Qd = Qs
750 – 25P = 50P – 300
1050 = 75P
P = € 14
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
Il prezzo di equilibrio per la pizza è di € 14 ed è quindi superiore a € 6, come richiesto
per evitare la chiusura della produzione. Il fatto che, in corrispondenza di tale prezzo,
l’impresa stia facendo profitti o meno, dipende esclusivamente dal minimo dei costi
medi. La nuova funzione del costo medio risulta: AC = Q/2 + 6 + 50/Q.
MC = AC
50 Q
Q6
6
Q 2
Q 50
2 Q
Q2 = 100
Q = 10
Il costo medio minimo corrisponde a € 16 (valutiamo AC o MC quando Q = 10), quindi le
imprese stanno perdendo denaro nel breve periodo, praticando un prezzo pari a € 14.
Ad un prezzo di € 14, Qd è data da 750 – 25(14) = 400. Siccome vi sono 50 imprese,
ognuna produrrà 8 pizze; nel breve periodo, quindi, le 50 imprese producono ciascuna 8
pizze, vendendo ognuna di esse a € 14.
A causa delle perdite registrate, le imprese decideranno di uscire dal mercato nel lungo
periodo: con la riduzione dell’offerta, il prezzo dovrà aumentare, fino a raggiungere i €
16 che corrispondono al costo medio minimo. Ad un prezzo pari a € 16, Qd sarà pari a
750 – 25(16) = 350. Siccome ogni impresa produrrà 10 pizze, rimarranno allora 35
imprese operanti sul mercato nel lungo periodo.
13.8
Nell’esercizio 13.7, le 15 imprese che lasciavano il mercato nel lungo periodo hanno ora
l’opportunità di chiudere già nel breve periodo. Esse continueranno a produrre nel breve
periodo, anche se in perdita, dal momento che tali imprese perdono meno quando
producono, piuttosto che quando arrestano la produzione. Se, tuttavia, l’affermazione
secondo cui “le imprese attive possono chiudere nel breve periodo” significa che tali
imprese possono recuperare i loro costi fissi già nel breve (in altre parole, vuol dire che
non vi sono costi sommersi), allora tutte e 15 le imprese decideranno di abbandonare
immediatamente il mercato, facendo salire il prezzo a € 16 e creando quindi in anticipo le
condizioni tipiche di una situazione di lungo periodo.
13.9
Affermare che un’innovazione ha incrementato le economie di scala significa affermare
che l’innovazione ha accresciuto il livello di produzione oltre il quale il costo medio
inizia a decrescere. Se il costo medio inizia a ridursi in corrispondenza di una quantità di
output maggiore, anche il valore di minimo della funzione del costo medio sarà raggiunto
in corrispondenza di un livello di produzione maggiore. Sapendo che, nel lungo periodo,
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
il prezzo coincide con il minimo del costo medio, possiamo allora concludere che lo
spostamento versa destra della funzione del costo medio comporta necessariamente un
aumento della scala di produzione efficiente per l’impresa. Ogni impresa produrrà
dunque di più nel lungo periodo, espandendo la dimensione dell’operatore medio sul
mercato di riferimento.
13.10
Se il costo totale si riduce di un euro per ogni livello dell’output, qualsiasi sia tale livello,
tale variazione equivale a una riduzione di € 1 nei costi fissi. Dato che i costi fissi non
sono considerati nel breve periodo (siccome non influenzano i costi marginali), non
dovremmo osservare alcun cambiamento né al prezzo di equilibrio, né all’output di
equilibrio per l’impresa nel breve periodo. L’unica variazione osservabile sarebbe
relativa ai profitti, che aumenterebbero di € 1.
Nel lungo periodo, questi profitti attireranno nuove imprese, desiderose di entrare
anch’esse sul mercato. Con il loro ingresso, il prezzo si ridurrà fino a diventare € 1/Q di
meno di quello che era precedentemente. Ci saranno più imprese, ognuna della quali
produrrà poco meno rispetto al livello di produzione del periodo precedente: l’output
complessivo risulterà però maggiore di prima e il prezzo scenderà inevitabilmente.
13.11
Il primo passo consiste nell’uguagliare offerta e domanda per poi risolvere per il prezzo
di equilibrio:
Qs = Qd
5P – 6 = 21 – 4P
9P = 27
P = € 3,00
Ad un prezzo di € 3, sia la domanda che l’offerta ammontano a 9 miliardi di bushel
l’anno. Consideriamo ora il più alto prezzo per il quale l’offerta risulta nulla e il più
basso prezzo per il quale la domanda risulta nulla. Possiamo determinare questi due
livelli di prezzo imponendo pari a zero sia Qd che Qs e risolvendo per il prezzo:
Qd = 21 – 4P
0 = 21 – 4P
4P = 21
P = € 5,25
Qs = 5P – 6
0 = 5P – 6
6 = 5P
P = € 1,20
Possiamo ora calcolare l’area dei due triangoli:
SC= ½(Q)(€ 5,25 – P)
SC = ½(9)(€ 5,25 – € 3)
SC = € 10,125
SP = ½(Q)(P – € 1,20)
SP = ½(9)(€ 3,00 – € 1,20)
SP = € 8,10
Microeconomia 2e
Douglas Bernheim, Michael Whinston
Copyright © 2012 – McGraw-Hill Education (Italy) srl
Il surplus aggregato è la somma del surplus del consumatore e di quello del produttore:
STOT = SC + SP
STOT = € 10,125 + € 8,10
STOT = € 18,225












