Caratteristica_diodo_studio a casa

Caratteristica voltamperometrica di un diodo – studio a casa
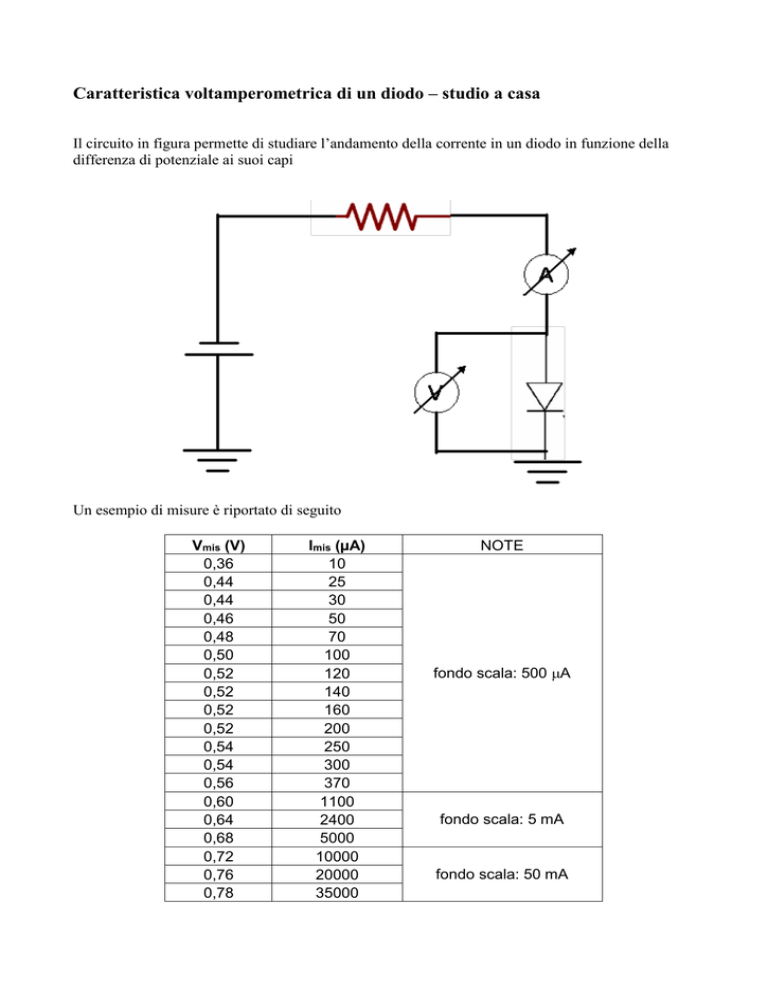
Il circuito in figura permette di studiare l’andamento della corrente in un diodo in funzione della
differenza di potenziale ai suoi capi
Un esempio di misure è riportato di seguito
Vmis (V)
0,36
0,44
0,44
0,46
0,48
0,50
0,52
0,52
0,52
0,52
0,54
0,54
0,56
0,60
0,64
0,68
0,72
0,76
0,78
Imis (µA)
10
25
30
50
70
100
120
140
160
200
250
300
370
1100
2400
5000
10000
20000
35000
NOTE
fondo scala: 500 A
fondo scala: 5 mA
fondo scala: 50 mA
La corrente nel diodo non è quella misurata all’amperometro in quanto il voltmetro presenta una
resistenza interna. In particolare il fondo scala del voltmetro era fissato sui 2V per cui la resistenza
interna del voltmetro era rv   20* fs  k   40 k . Poiché la resistenza dinamica del diodo è molto
alta prima della fase di conduzione, ci aspettiamo che le correzioni maggiori siano per piccoli valori
V
V
di corrente misurata. Poiché si ha I mis  I v  I d  mis  I d  I d  I mis  mis . Con questa correzione
rv
rv
si ha la seguente tabella di valori:
Vmis (V)
0,36
0,44
0,44
0,46
0,48
0,50
0,52
0,52
0,52
0,52
0,54
0,54
0,56
0,60
0,64
0,68
0,72
0,76
0,78
Imis (µA)
10
25
30
50
70
100
120
140
160
200
250
300
370
1100
2400
5000
10000
20000
35000
Iv (µA)
9
11
11
12
12
13
13
13
13
13
14
14
14
15
16
17
18
19
20
Id (µA)
1
14
19
39
58
88
107
127
147
187
237
287
356
1085
2384
4983
9982
19981
34981
È possibile adesso graficare i valori di Id in funzione di Vmis.
Caratteristica voltamperometrica di un diodo al silicio
40000
35000
Id (  A)
30000
25000
20000
15000
10000
5000
0
0,25
0,35
0,45
0,55
Vm is (V)
0,65
0,75
0,85
Dal grafico si evince che la corrente nel diodo è molto piccola per valori della d.d.p. ai suoi capi
minori di circa 0.6V, mentre cresce rapidamente per valori maggiori. Il valore 0.6 è detto appunto
“ginocchio” o “soglia” di potenziale del diodo. Con il software Logger Pro è possibile approssimare
i dati con una funzione del tipo I V   A  e BV  1 . Il parametro A rappresenta la corrente di
1
. La costante  vale circa 2
VT
kT
T
per il silicio mentre VT è detto equivalente in Volt della temperatura e vale VT 
. Con

q 11600
le misure in esame si ha: A   0,002  0,001  A e B   21, 4  0,9 V 1 . Il valore della corrente di
saturazione inversa è compatibile con zero contro il valore atteso di qualche centinaio di nA. Il
risultato è compatibile con il fatto che tale valore atteso è confrontabile con la sensibilità dello
strumento a disposizione per cui non è possibile una stima accurata di questo parametro. Per quel
che riguarda l’equivalente in volt della temperatura dalle misure si ottiene
1
VT mis   0, 023 V
2B
contro il valore atteso 0,025 V alla temperatura di 293 °K. Tale
B
 VT mis  VT mis
 0, 001 V
B
risultato è compatibile con il valore atteso e può considerarsi una buona stima del parametro. Una
stima migliore poteva essere ottenuta effettuando la misura della caratteristica del diodo utilizzando
anche la configurazione con l’amperometro a valle del voltmetro. In questo caso andava tenuto
conto della resistenza interna dell’amperometro che con fondo scala a 50mA diventava
confrontabile con la resistenza differenziale del diodo per quell’intervallo di corrente (circa 6 ).
Una stima della resistenza differenziale del diodo può essere ottenuta ricordando che:
saturazione inversa del diodo, mentre il parametro B è tale che: B 
V
VT
I  I0
dI I 0 e


. Nella regione di misura risulta sempre I I 0 da cui segue
dV
VT
VT
V
1
rd  T 
. Per correnti dell’ordine di I  10  A (ben al di sotto della tensione di soglia) si ha
I
BI
r  47k il che conferma che la resistenza del voltmetro era dell’ordine di grandezza di quella del
diodo per cui il suo effetto in questa configurazione non era affatto trascurabile. Per correnti
dell’ordine di I  10 mA (al di sopra della tensione di soglia) si ottiene r  5  il che conferma che
la resistenza dell’amperometro è dell’ordine di grandezza di quella del diodo per cui il suo effetto
nella configurazione (qui non indagata) “amperometro a valle” non sarà trascurabile.
Un altro modo per determinare la resistenza del diodo è quello dell’approssimazione lineare. In
Vmis  0, 6 V
particolare si può suddividere l’intervallo di misura in due parti:
e approssimare a
V mis  0, 6 V
rette gli andamenti sperimentali. Per valori di V minori della tensione di soglia si ottiene
Semplificando
si
ha:
I d  aVmis  b; a  14  3 102 V 1 A; b   6  1 102  A .
rd 1  g d 
a  14  3 10-4 1; b   6  1 10-1mA Segue subito che la resistenza diretta R f (cioè ottenuta
mediante approssimazione lineare a tratti della caratteristica) per piccoli valori di corrente vale
R f   7  2  102  . Naturalmente questo valore non può essere confrontato con quello ottenuto
precedente della resistenza dinamica in quanto trattasi di una approssimazione molto poco accurata.
Per
valori
di
V
maggiori
della
tensione
di
soglia
si
ottiene
5 1
4
Semplificando
si
ha:
I d  cVmis  d ; c  1, 4  0,3 10 V  A; d   8  2 10  A .
c  1, 4  0,3 101 1; d   8  2 10 mA da cui segue che R f   7  1  , valore di resistenza
per un diodo in conduzione accettabile. Dalle stime dei parametri c e d è possibile infine
determinare la tensione di soglia del diodo. In particolare basterà trovare il valore di Vmis , che
d
chiameremo V tale che I d  0 . Segue subito che tale valore è cV  d  0  V   . Si ottiene
c
subito V   0.6  0.1 V che è compatibile con il valore atteso di 0,65 V . Da notare che per la
determinazione dell’errore su Voccorrerebbe tenere conto della covarianza dei due parametri c e d.
Il riepilogo dei fit effettuati è riportato nella figura seguente
Un altro metodo per determinare la tensione di soglia e la resistenza diretta è quello di sfruttare la
definizione di resistenza dinamica. In particolare, si tratta di determinare la retta tangente alla curva
di fit dei dati sperimentali in un punto opportuno Vx in modo tale che la sua intersezione con l’asse
del potenziale sia proprio la tensione di soglia. Conoscendo la caratteristica voltamperometrica
ideale del diodo, è possibile determinare teoricamente il punto Vx e quindi la retta tangente ed
ottenere una stima sperimentale della tensione di soglia e della resistenza diretta. Abbiamo visto che
 VV

la caratteristica voltamperometrica attesa per un diodo al silicio è I V   I 0  e T  1 , e la tensione




Vx
VT
I 0e
V q
VT
dove q va calcolato imponendo la condizione di appartenenza del punto di tangenza alla curva data.
di soglia è V  0.65 V . La retta tangente a I V  nel punto Vx ha equazione y V  
Vx
 Vx

 Vx 
I eVT
V  
Vx  q  I 0  eVT  1 da cui segue q  I 0  eVT 1  x   1 . Il valore
Si ha quindi y Vx   0



VT
 VT  



Vx deve essere determinato imponendo che la retta tangente intersechi l’asse del potenziale nel
 VVx

Vx
Vx  
e T
VT 
V  e 1 
punto V  0.65 V . Quindi si deve avere y V   0  I 0 
  1  0 che

V

V
T
T

 



Vx
 

restituisce l’equazione implicita V  Vx  VT  e VT  1 . L’equazione potrebbe essere risolta




numericamente o per via grafica; scegliamo di risolverla tenendo conto che Vx deve essere un
valore vicino a V (ad esempio circa 1V) per cui, tenendo conto che   2 e VT  0.025 V

1
2*0.025
103

50
l’esponenziale vale circa e
e
 e20 1 per cui la condizione implicita può essere
riscritta come V  Vx  VT  Vx  V  VT . Con questa approssimazione la retta tangente alla
caratteristica voltamperometrica del diodo nel punto Vx così calcolato si potrà scrivere come
 V VT V  V  
y V   I 0  e VT
 1 . Questa retta intersecherà l’asse del potenziale nel punto V * tale


VT


V VT
V
*


1
V  V  

VT
VT
*
 1  0 cioè V  V   VT e
che  e
. V * differirà da V di un valore


VT


VT

V
1

V
VT
V
e
 13 , l’errore percentuale che si
. Ora poiché
V
V
VT
VT
commette sostituendo al valore esatto quello approssimato di Vx è dell’ordine di 10-7, perfettamente
accettabile per le stime in gioco. Quindi, per il seguito si determinerà la retta tangente alla curva di
fit I V   A  e BV  1 nel punto Vx  0.7 V . Tale retta, in termini dei parametri del fit sarà scritta
percentuale pari a
e
VT
 e 1
come y  A  Be0.7 BV  e0.7 B 1  0.7 B   1 . Essa intersecherà l’asse del potenziale nel punto
e0.7 B 1
e 0.7 B
 . Ora, il termine
è molto minore degli altri due e può essere trascurato
B
B
B
1
per cui la stima della tensione di soglia è V *  0.7   0.65 V con errore tale che
B

B
V *  V *
 0.03V . La stima ottenuto dipende solo dal parametro B ed è una stima migliore di
B
quella ottenuta in precedenza. Si può fare anche un discorso analogo per stimare in maniera più
V *  0.7 
accurata dai dati sperimentali la resistenza dinamica del diodo. In generale, la resistenza dinamica
V
I eVT
sarà data dall’inverso della pendenza della retta tangente, cioè 0
VT
od anche, utilizzando i
parametri del fit, ABe BV . Per stimarne un valore approssimato quando il diodo è conduzione, è
1
possibile valutare tale pendenza quando V  Vx  0.7V . Si avrà quindi R f 
. Con le stime
ABe0.7 B
di A e B si ha R f   7.3  0.3  dove anche in questo caso si è trascurata la covarianza dei due
fattori. Per stimarne un valore approssimato quando il diodo è in interdizione è possibile valutare
tale pendenza quando V  V , ad esempio quando V  0.3 V che ci assicura di essere ben lontani
dal valore di soglia, quindi in un intervallo in cui la corrente attraverso il diodo varia poco qualsiasi
sia la tensione applicata. In questo caso, con le stime di A e B si ha R f   38  2 k , valore simile
a quello stimato più sopra.