Lavoro e Potenza, Unità di misura
Com’è noto, la Potenza è definita come Lavoro (= Forza · spostamento)
nell’unità di tempo.
L’unità SI della potenza è dunque:
1 Watt = 1 N · m /sec
Nelle unità MKS, la potenza (la cui unità non ha un nome) è invece:
1 unità di Potenza = 1 kgf · m /sec
Nella pratica sono ancora largamente diffuse le unità Cavallo Vapore
(CV) in Europa ed Horse Power (HP) nei paesi anglosassoni.
Si ha, per definizione:
1CV = 75 kgf m / sec
1 HP = 33000 lbf· ft / min
Da cui:
1 CV = 75 · 9.81 Newton m /sec =735.75 Joule /sec [Watt]
1 kW = 1.36 CV
Allo stesso modo, convertendo opportunamente le unità inglesi, si ha:
1 HP = 745.7 Watt
1 kW = 1.34 HP
Lavoro nell’unità di tempo fornito da un uomo = 30 60 W 0.05 0.1 CV
Lavoro nell’unità di tempo fornito da un cavallo = 300 450 W 0.4 0.6 CV
Lavoro nell’unità di tempo fornito da un bue = 1000 1500 W 1.5 2 CV
Lavoro nell’unità di tempo fornito da ruota ad acqua = 1.5 3.8 kW 2 5 CV
Lavoro nell’unità di tempo fornito da mulino olandese =1.5 10.5 kW 2 15 CV
La prima metà del XVIII secolo segna il vero inizio della
Termodinamica, intesa come la scienza della trasformazione continuativa
(cioè mediante una macchina) del calore in lavoro meccanico.
Nel campo della Termodinamica la macchina di Watt riveste
un’importanza fondamentale, essendo la prima macchina in cui il fluido di
lavoro evolve in un circuito sigillato.
L’interesse degli studiosi di Termodinamica si appuntò quindi sul ciclo di
trasformazioni seguito dal fluido di lavoro; è evidente infatti che un
aumento del rendimento di conversione, inteso come rapporto tra il calore
fornito alla macchina ed il lavoro meccanico da essa prodotto, può essere
conseguito non solo attraverso una migliore lavorazione degli organi
meccanici (miglioramento delle tenute, degli isolamenti, diminuzione degli
attriti) ma soprattutto attraverso l’individuazione del ciclo di
trasformazioni più conveniente da fare eseguire al fluido all’interno della
macchina.
Pertanto, mentre il raggiungimento del primo obiettivo è limitato
esclusivamente dalle tecnologie di lavorazione disponibili, il secondo
necessita della definizione delle leggi fondamentali che regolano la
trasformazione continuativa di quella particolare forma di energia, che è
appunto il calore, in lavoro meccanico.
Lo studio delle trasformazioni subite dal fluido durante il ciclo di lavoro
necessita però degli strumenti necessari per definirne univocamente le
condizioni all’interno dei diversi organi che compongono la macchina.
Stato di un fluido
La definizione dello “stato” di un fluido necessita della conoscenza di
alcuni “parametri di stato” che devono essere in numero necessario e
sufficiente per consentire all’osservatore di accertare se in due punti
qualsiasi della macchina il sistema fluido si trovi o no nelle stesse
condizioni.
Il numero di questi parametri di stato dipende evidentemente dalla
complessità del sistema o meglio dalla complessità del modello che si
vuole utilizzare per rappresentare il sistema stesso.
Partendo da queste ipotesi sono possibili due diversi approcci alla
definizione dello stato del sistema:
Approccio microscopico: considera il sistema formato da numerose
particelle in condizioni di equilibrio ed applica i metodi statistici
propri della teoria cinetica dei gas. E’ in grado di spiegare il perché
di alcuni fenomeni, ma necessita della conoscenza approfondita del
comportamento della particella-tipo a cui applicare i metodi statistici.
Approccio macroscopico: considera il sistema come un fluido
continuo e ne valuta lo stato in relazione alle azioni che il sistema nel
suo complesso esercita verso l’esterno. Fa uso di un numero
estremamente ridotto di “indicatori globali” o “parametri
macroscopici di stato” ma non è in grado di spiegare il meccanismo
di alcuni fenomeni.
In questo corso verrà utilizzato l’approccio macroscopico o della
“Termodinamica Classica”, anche se spesso si farà ricorso ai metodi
della Termodinamica microscopica per una migliore comprensione dei
fenomeni in studio.
Come si è detto, l’approccio macroscopico allo studio della
Termodinamica dei sistemi in equilibrio prende in considerazione le
interazioni tra il sistema nel suo complesso e l’ambiente esterno.
Considerando il sistema composto da un fluido omogeneo chimicamente
definito (p.es. un gas), contenuto in un recipiente che lo separa
dall’esterno, i parametri misurabili che caratterizzano il sistema possono
facilmente ridursi a:
-
la massa del sistema, facilmente determinabile mediante pesatura;
-
il volume del sistema, facilmente determinabile mediante misure di
lunghezza;
-
la forza esercitata dal sistema sulle pareti del recipiente, facilmente
determinabile mediante misure di forze.
Queste grandezze sono di per sé grandezze estensive in quanto dipendono
dalla quantità di materia che costituisce il sistema. E’ facile ridurre queste
ultime a grandezze intensive:
-
la densità, definita come la massa dell’unità di volume;
-
il volume specifico, definito come il volume dell’unità di massa;
-
la pressione, definita come la forza che il sistema esercita sull’unità
di superficie del recipiente.
E’ facile rendersi conto che, oltre queste, non ci sono altre grandezze
macroscopiche misurabili direttamente.
Si ricordi che, data l’ipotesi di equilibrio interno del sistema, le suddette
grandezze intensive devono avere lo stesso valore in qualunque punto del
sistema esse vengano misurate.
1
Concetto di Pressione : Approccio microscopico
Un contenitore di forma sferica (1) contiene N molecole di massa m.
Ipotesi:
1) le dimensioni delle particelle sono piccolissime in confronto alla distanza
media tra le particelle => particelle puntiformi.
2) la probabilità che le particelle urtino tra loro è trascurabile => le particelle
urtano solo con le pareti del contenitore.
3) gli urti sono perfettamente elastici.
r
i
vi
Mediante il teorema dell’impulso è possibile calcolare la forza Fi esercitata in
direzione radiale dalla i-esima particella sul contenitore:
Fi
mi vi cosi mi vi cosi
i
essendo 1/i la frequenza degli urti.
La forza esercitata dalle particelle sulla superficie interna del contenitore sarà allora:
N 2 mi v i cos i
Ftot
i 1
i
e la pressione P:
P
1
N 2m v cos
i i
i
4 r 2 i 1
i
e poiché la distanza tra due collisioni successive può scriversi: l i 2r cos i
l
i i
vi
2r cos i
vi
pertanto la pressione può scriversi:
1
E’ possibile dimostrare che le relazioni qui esposte sono valide per un contenitore di forma qualsiasi
P
N mv2
i i
1
4 r 2 i 1
r
1
N
mi vi
2
4 r 3 i 1
ed essendo V = 4/3 r3 il volume interno della sfera,
1 N
PV mi vi 2
3 i 1
2 N1
2
mi vi
3 i 1 2
2
N Ecin
3
La pressione P è legata al valore dell’Energia Cinetica media nel volume V.
Fatta la seguente posizione:
2
N Ecin Cost T
3
e quindi
PV Cost T
viene definita la caratteristica macroscopica intensiva Temperatura.
La Temperatura viene definita come un indice dello stato di agitazione delle
molecole.
Si vuole sottolineare la dizione “caratteristica macroscopica” in quanto la
grandezza temperatura di un sistema (come la Pressione) ha senso soltanto se viene
intesa come il valore medio dell’energia cinetica calcolato per un sistema composto
da un numero molto grande di particelle.
Lo stato di un sistema costituito da N molecole, per cui siano valide le ipotesi sopra
indicate, può essere definito mediante le caratteristiche macroscopiche [Pressione,
Volume e Temperatura] legate tra loro dalla relazione di stato : PV = Cost T.
Il valore della Costante dipende dalle caratteristiche fisiche delle molecole che
compongono il sistema (nonché dal sistema di riferimento).
Non è possibile misurare direttamente la Temperatura
L’affermazione precedente è giustificata dal fatto che una misura diretta della
temperatura necessiterebbe della conoscenza dei 6N parametri che definiscono lo
stato del sistema dal punto di vista meccanico.
La Temperatura di un sistema [P,V,T] di cui sia nota l’equazione di stato f(P,V,T)=0
può essere calcolata (in una scala arbitraria) attraverso i valori fisicamente misurabili
dei parametri macroscopici Pressione e del Volume del sistema.
E’ necessario conoscere l’equazione di stato di ogni sistema (equazione
che può essere anche assai complessa) per calcolarne la Temperatura ?
“Legge Zero” della Termodinamica
Siano A e B due sistemi (P,V,T) in equilibrio termico interno.
Sia nota la relazione f (P,V,T) = 0 di ciascuno dei due sistemi.
A
T1 =f (P1,V1)
B
T2 =f (P2,V2)
Siano T1 e T2 le temperature di
A e di B (in una scala qualsiasi)
ottenute in base alla relazione di
stato propria di ciascuno dei due
sistemi.
Si supponga T1 T2
Si osserva che, mettendo a contatto i due sistemi attraverso una parete
termicamente non isolante, le variabili di stato P e V di ciascun sistema si
modificano (per quanto i vincoli lo permettono) fino a che ognuno dei due
sistemi raggiunge un nuovo stato di equilibrio.
A
T= f (P’1,V’1)
B
T= f (P’2,V’2)
In questo stato di equilibrio le temperature
dei due sistemi sono eguali.
(Verifica sperimentale)
La “LEGGE ZERO” stabilisce che : se due sistemi sono in equilibrio
termico con un terzo sistema, sono anche in equilibrio termico tra loro.
A
(PA,VA)
B
(PB,VB)
C
(PC,VC)
L’importanza della Legge “Zero” consiste nel fatto che è possibile stabilire se due
sistemi sono in equilibrio termico tra loro senza metterli direttamente a contatto,
ma utilizzando un terzo sistema (che potremo chiamare termometro).
Effettuata la scelta del termometro (sistema, grandezza termometrica, funzione
termometrica), la temperatura di qualunque corpo o sistema sarà definita attraverso le
condizioni in cui si verrà a trovare il termometro posto in equilibrio termico con esso.
La “Legge Zero” è la base del concetto di misura della temperatura
Si osservi che l’uso del termometro è in qualche modo “distruttivo” della grandezza
che si vuole misurare. Infatti la temperatura di un sistema misurata dal termometro
non è più quella originale del sistema ma quella (eguale) che il sistema ed il
termometro possiedono quando insieme raggiungono le condizioni di equilibrio.
f(P,V,T)=0
A
f (T) = ??
B
f (T)=??
Un’altra conseguenza notevole è che non è più necessario conoscere le relazioni di
stato dei sistemi A e B, ma solo quella del termometro.
Supponiamo di possedere un sistema S il cui stato è definito dai parametri intensivi P,
v e T, e supponiamo ancora di conoscere la relazione T = f(P,v) del sistema.
Possiamo utilizzare questo sistema come “Termometro” .
Le cose si semplificano se manteniamo costante uno dei parametri.
Posto il Termometro in equilibrio termico con ciascuno dei due sistemi di riferimento
V = cost
T = f(P)solo
P = cost
T = f(V)solo
Trif 2
P(P
Trif 2
S
Trif 1
Trif 1
S
Rif.1
Rif.2
è possibile segnare sulla scala graduata due valori numerici arbitrari.
Se i due sistemi di riferimento contenessero acqua in due diverse condizioni fisiche
Rif. 1 = ghiaccio fondente alla pressione ambiente (1 atm)
Rif. 2 = acqua bollente alla pressione ambiente (1 atm)
potremmo attribuire il valore numerico 0 a Trif1 ed il valore numerico 100 a Trif2.
Suddividendo – sempre arbitrariamente - la scala in 100 parti, in maniera lineare,
otterremo la cosiddetta scala Centigrada (o scala Celsius).
Usando sistemi di riferimento diversi o adottando valori numerici diversi potremo
ottenere altre scale termometriche.
P.es. un termometro basato sulla scala Fahrenheit, definita su punti di riferimento
diversi, segnerebbe un valore numerico di 32°F sul punto di riferimento a 0°C e
segnerebbe 212°F sul punto di riferimento a 100°C.
Si ricordi che suddividere la scala in maniera lineare non implica che il
comportamento del sistema termometrico nei riguardi della temperatura sia
anch’esso lineare.
Di conseguenza i valori segnati dai due termometri(a P e a V costante) devono
coincidere ai punti di riferimento, ma possono essere diversi nei punti intermedi.
(Un sistema con una temperatura a metà tra Rif.1 e Rif.2 potrebbe essere indicato
con 49°C da un termometro e con 51°C dall’altro.)
Sistema Termodinamico
Sistema
L
L
Gu
Q
Sistema Chiuso
Gi
Q
Sistema Aperto
Sistema Isolato
- - - - - - - - - - - Contorno del sistema : definisce il “volume di controllo”
Un sistema Chiuso ed un sistema Isolato sono a Massa Costante.
Un sistema Aperto non è (in generale) a Massa Costante.
Caso particolare : un Sistema Aperto con flusso a regime (Gi = Gu) è a Massa costante
Trasformazioni quasi-statiche
dx
dm
P-dp
v+dv
P, v
Consentono di passare, mediante squilibri infinitesimi, da uno stato iniziale di
equilibrio (1) ad uno stato finale di equilibrio (2) attraverso una serie (infinita) di stati
di equilibrio
P
P
1
1
2
v
Trasformazioni aperte
2
v
Trasformazioni chiuse (cicli)
ENERGIA INTERNA DI UN SISTEMA CHIUSO
L’Energia Interna E di un sistema chiuso è data dalla somma di tutte le possibili forme di Energia
possedute dal sistema stesso.
Se il sistema di massa m
- è in moto con velocità u, possiede l’Energia Cinetica Ecin
1
mu 2
2
- è posto alla quota z rispetto alla quota di riferimento, possiede l’Energia Potenziale
E pot m g z
- può essere soggetto a reazioni chimiche, possiede l’Energia Chimica Echimica
- può essere soggetto a reazioni nucleari, possiede l’Energia Nucleare Enucleare
Tutte queste forme di energia sono possedute dal sistema nel suo complesso
Tuttavia il sistema possiede ancora dell’altra energia interna che viene generalmente indicata con la
lettera U.
L’energia interna U è l’energia posseduta dai costituenti elementari del sistema.
Per esempio, nel caso di un gas, la U (la cui natura meccanica è evidente) include:
-
l’energia cinetica dei moti traslazionali, rotazionali e vibrazionali delle molecole,
l’energia potenziale che deriva dalle mutue forze attrattive tra le molecole.
Pertanto l’Energia Interna totale di un sistema può scriversi:
E = U + Ecin + Epot + Echimica + Enucleare
Poiché nel nostro corso (se non esplicitamente dichiarato) tratteremo di sistemi termodinamici non
in movimento, posti al livello di riferimento, chimicamente non reagenti né soggetti a reazioni
nucleari, parlando di Energia Interna, faremo riferimento alla sola U.
Per calcolare il valore dell’Energia Interna U di un sistema è necessario – come è stato già detto conoscere, istante per istante, la posizione e la velocità di ciascuno dei componenti elementari del
sistema stesso e quindi il suo stato microscopico, mentre i valori numerici delle energie cinetica e
potenziale dipendono dal sistema di riferimento arbitrariamente scelto.
E’ evidente allora che: 1) L’Energia Interna U è una funzione dello stato del sistema;
2) L’Energia Interna è nota a meno di una costante;
3) E’ impossibile definire direttamente il valore dell’Energia Interna.
L’ultima affermazione ricorda quella fatta precedentemente riguardo lo stato microscopico del
sistema.
Riprendendo in esame il caso semplice di un gas, ossia di un generico sistema (P,V,T) è facile
intuire che l’energia interna U è univocamente determinata (costante arbitraria a parte) dai valori
della Pressione, della Temperatura e del Volume del sistema.
U = U(P,V,T)
Dalla prima affermazione ricaviamo anche :
Il differenziale di U, fatto rispetto ad una qualsiasi coppia di variabili di stato è un differenziale
esatto e gode quindi di tutte le proprietà matematiche possedute dai differenziali esatti o totali
2
dU U 2 U1
dU 0
1
Ciò significa che, andando da uno stato di equilibrio ad un altro (cioè da un punto nello spazio PVT
ad un altro), la variazione di Energia Interna è indipendente dal cammino seguito.
LAVORO IN UN SISTEMA CHIUSO
A differenza dell’Energia Interna, che è una proprietà del sistema, ed è posseduta dal sistema,
Il Lavoro è Energia in transito attraverso i contorni del sistema.
Ciò significa che il lavoro esiste solo mentre viene scambiato dal sistema; una volta che l’Energia
meccanica è stata ricevuta o ceduta dal sistema essa si è trasformata in una variazione di Energia
Interna del sistema stesso.
Ci sono molti modi di scambiare lavoro con un sistema: si può, per far qualche esempio,
comprimere un gas, magnetizzare un pezzo di ferro, caricare una batteria, stirare un filo o piegarlo,
agitare un recipiente contenente un liquido.
In ognuno di questi esempi si può riconoscere il prodotto di una forza F generalizzata per uno
spostamento generalizzato:
2
L1, 2 F( x ) dx
1
Nel caso di un sistema (P,V,T) contenuto in un cilindro munito di pistone, che costituisce il
contorno (mobile) del sistema, si avrà:
P
F
1
P1
P
A
L ( P A ) dl P dV
2
L1,2 P dV
P2
P
2
1
V1
dV
V2
V = Al
E’ facile rendersi conto che il Lavoro non è una funzione
P
degli stati iniziale e finale della trasformazione, non è una
proprietà del sistema ovvero non è una funzione di stato.
1
P1
Infatti il lavoro, essendo rappresentato dall’area sottesa
dalla curva che rappresenta la trasformazione, dipende dal
cammino seguito.
P2
2
L trasf L
1
2
V1
V2
Per indicare una quantità infinitesima di Lavoro useremo il simbolo L e non dL, proprio per
ricordare che non stiamo parlando di un differenziale esatto, calcolato rispetto ad una qualsiasi
coppia di variabili di stato ma soltanto di una quantità infinitesima.
E’ ovvio che l’espressione L = PdV è valida in generale,
dn
qualunque sia la forma del recipiente in cui il sistema (chiuso) è
d
contenuto.
P
B
A
Si consideri infatti un sistema avente pressione uniforme P
contenuto in un recipiente A di forma qualsiasi.
Si consideri poi una trasformazione infinitesima del sistema
durante la quale le pareti del recipiente si portino dalla posizione iniziale A ad una posizione finale
B lasciando così espandere il sistema in esso contenuto.
Sia d un elemento infinitesimo di superficie del recipiente e sia dn lo spostamento di questo
elemento nella direzione normale alla superficie del recipiente.
Il lavoro fatto sull’elemento di superficie d dalla pressione P durante lo spostamento dei contorni
dalla posizione A alla posizione B è ovviamente P ·d ·dn (d ·dn è un volumetto infinitesimo).
Il lavoro totale fatto durante la trasformazione infinitesima si ottiene integrando l’espressione
precedente su tutta la superficie del recipiente; poiché P è una costante si ottiene:
L P d dn
Ora è evidente dalla figura che la variazione dV di volume del recipiente è data dall’integrale di
superficie
dV d dn
V
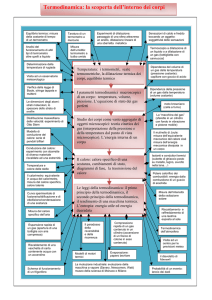
“ Il lavoro è energia in transito attraverso i confini del sistema, che può essere
ridotta al solo ed unico effetto di variare il livello di un peso”
La definizione sottolinea il fatto che tutte le forme di lavoro sono equivalenti e pertanto una forma
di energia è riconoscibile come lavoro quando è riconducibile tutta e soltanto ad una delle più
evidenti forme di lavoro meccanico: quello da spendere per innalzare la quota di un grave.
----------- Contorni del sistema
Nella figura la batteria di accumulatori rappresenta il sistema chiuso dal quale preleviamo Energia.
La corrente che scorre nel circuito provoca il riscaldamento della resistenza; l’Energia ceduta dalla
batteria si è convertita tutta in calore sulla resistenza; oltre a questa cessione di Energia, la batteria
non ha subito alcuna altra modifica.
Si noti che il sistema è chiuso in quanto gli elettroni che hanno attraversato la resistenza sono
tornati tutti nella batteria. (Il sistema è pertanto a massa costante).
Ci chiediamo: l’Energia che ha attraversato i contorni del sistema è Calore o Lavoro?
Utilizzando un motore elettrico ideale (privo di attriti meccanici e di resistenza elettrica) è possibile
convertire la stessa quantità di Energia che abbiamo usato per riscaldare la resistenza, in Energia
potenziale del grave mentre il motore elettrico non subisce alcuna modifica
Pertanto la stessa quantità di Energia che aveva attraversato i contorni del sistema nel primo caso è
diventata ora tutta Energia Potenziale (meccanica) senza avere prodotto altri effetti o modifiche né
all’esterno né all’interno del sistema.
Pertanto : l’Energia che ha attraversato i contorni del sistema è Lavoro.
Per ciò che riguarda il segno convenzionale da attribuire all’Energia che viene scambiata da un
sistema con l’esterno sotto forma di Lavoro, è evidente che lo studioso di Termodinamica è più
interessato a ciò che succede dentro il sistema quando l’esterno compie lavoro su di esso e ritiene
più logico considerare positivo il lavoro fatto sul sistema dall’esterno.
Un Ingegnere invece preferisce chiedersi quanto lavoro può aspettarsi di ricavare da un sistema e
pertanto considera positivo il lavoro fornito dal sistema all’esterno.
In questo corso viene adottato il secondo punto di vista, quindi per convenzione stabiliamo che:
L è positivo se è fatto dal sistema (lavoro uscente dal sistema = positivo)
L è negativo se è fatto sul sistema (lavoro entrante nel sistema = negativo)
-
Questa convenzione sembra peraltro più naturale quando si consideri il lavoro scambiato da un gas
che viene fatto espandere all’interno di un cilindro munito di pistone.
Con una variazione positiva (aumento) del volume il sistema fornisce lavoro (positivo) all’esterno.
L PdV 0 con dV 0
P
2
L1, 2 P dV
P1 1
(espansione ) 0
1
1
L 2,1 P dV
+
P2
2
L tot P dV
2
V1
(compress ione ) 0
V2
(Area del Ciclo ) 0
V
La convenzione adottata in questo corso è quella adottata dai testi di Termodinamica
prodotti in Europa. I testi anglosassoni usano la convenzione opposta.
Calore
A differenza dell’Energia Interna, che è una proprietà del sistema, ed è posseduta dal
sistema,
il Calore è Energia in transito attraverso i contorni del sistema
(a causa di una differenza di temperatura).
Ciò significa che il calore esiste solo mentre viene scambiato dal sistema; una volta
che il Calore è stata ricevuto o ceduto dal sistema, esso è divenuto una variazione di
Energia Interna del sistema stesso.
Come vedremo in dettaglio nel seguito, le modalità di trasmissione del calore sono:
- Conduzione (nei mezzi solidi)
- Convezione (negli aeriformi)
- Irraggiamento (nel vuoto o in un mezzo non assorbente)
Come il Lavoro, anche il Calore non è una funzione degli stati iniziale e finale
della trasformazione, dipende dal cammino seguito, non è una proprietà del sistema
2
Q trasf Q
1
quindi non è una funzione di stato.
Per indicare una quantità infinitesima di Calore useremo il simbolo Q e non dQ,
proprio per ricordare che non stiamo parlando di un differenziale esatto, calcolato
rispetto ad una qualsiasi coppia di variabili di stato ma soltanto di una quantità
infinitesima.
Per convenzione si stabilisce che:
- Q è positivo se è ricevuto dal sistema (calore entrante nel sistema =
positivo)
- Q è negativo se è ceduto dal sistema (calore uscente dal sistema =
negativo)
La convenzione adottata in questo corso è quella adottata da tutti i testi di
Termodinamica prodotti nel mondo.
In questo corso definiremo “adiatermico” un processo che si svolge senza scambio
di calore tra il sistema e l’esterno e definiremo “adiabatico” un processo che si
svolge senza scambio di calore tra il sistema che si mantiene sempre in condizioni
di equilibrio termico interno e l’esterno.
I testi anglosassoni definiscono invece “adiabatic” qualunque processo che si svolga
senza scambio di calore tra il sistema e l’esterno.
L
Ritornando alla regola suggerita da J.H. Keenan per la individuazione della
forma di energia scambiata da un sistema, osserviamo che, durante una
espansione isoterma di un gas perfetto (come sarà chiarito nel seguito) si
ha una conversione totale dell’Energia che ha attraversato - sotto forma di
Calore - i contorni del sistema, in Lavoro meccanico.
Si ha infatti, con riferimento al sistema:
Qassorbito = Lprodotto
Anche qui, come nell’esempio dell’accumulatore, una forma di Energia è
stata trasformata tutta in energia potenziale meccanica (innalzamento del
peso).
Q
La differenza evidente è che, mentre nel caso precedente il motore elettrico
ideale alla fine del processo non aveva subito alcuna modifica,
(cosicché nessuno, guardando soltanto il motore, avrebbe potuto
affermare che esso era stato utilizzato e quanto lavoro avesse prodotto),
ora il gas si è espanso, quindi sistema si è modificato.
Termostato T
Ciò dimostra che l’Energia che ha attraversato i contorni del sistema non era Lavoro.
La conversione totale di Calore in Lavoro è possibile (come vedremo essa è insita
nel I° Principio della Termodinamica) ma non può essere realizzata come solo ed
unico effetto.
Nel seguito ci occuperemo della trasformazione continuativa di Calore in Lavoro.
Come vedremo ciò è possibile solo attraverso l’uso di una macchina che opera facendo eseguire ad
un fluido di lavoro un ciclo chiuso di trasformazioni.
Per determinare le leggi generali che regolano la trasformazione di calore in lavoro utilizzeremo
come fluido di lavoro per le nostre macchine, un fluido la cui equazione di stato è particolarmente
semplice e facile da determinare: il gas perfetto.
Leggi dei Gas Perfetti
Termostato
T
Nel 1662, Boyle, lavorando con diversi gas a temperatura costante (misurata in una scala arbitraria),
trovò che la Pressione ed il Volume possono considerarsi tra loro inversamente proporzionali ed il
loro prodotto pari ad un coefficiente che può dipendere solo dalla temperatura e dalla natura del gas.
Supponendo che questo comportamento sia valido per qualunque valore di P e di V, si avrebbe per
tutti gas:
PV = (t)
(t = costante)
Nel 1787, Charles, lavorando con diversi gas a pressione costante, trovò che il Volume del gas può
essere considerato direttamente proporzionale alla sua temperatura (misurata in una scala arbitraria)
secondo un coefficiente che può dipendere solo dalla pressione e dalla natura del gas. Si avrebbe
allora per tutti i gas:
V = (P)t
(P = costante)
Dalle due relazioni si può ricavare facilmente:
P V ( t )
V / t ( p)
e quindi
1
(t ) P (P) (sempre con P e t qualsiasi ) C
t
Sarà pertanto
Boyle)
Charles)
PV = C t
V = Ct / P
(t = costante)
(P = costante)
Per un dato gas, la costante C ha lo stesso valore nei processi a t o a P costante
Nel 1802, Gay-Lussac, lavorando con diversi gas a volume costante, trovò una relazione simile a
quella di Charles ed osservò che le relazioni tra la Pressione del gas e la sua temperatura (misurata
in una scala arbitraria) possono essere considerate lineari.
Si potrà scrivere allora, per tutti i gas:
P(t) = P0(1 + t)
(V = costante)
Supponendo di usare la scala centigrada per le misure di temperatura, P 0 rappresenta il valore
(diverso per ogni gas) della Pressione misurata a 0 °C su ciascuna isocora.
Usando gas diversi, Gay-Lussac osservò che, estrapolando gli andamenti delle diverse isocore, tutte
le linee tendono a riunirsi in un punto posto 273,15 °C al di sotto dello zero della scala centigrada.
Poiché questo comportamento è comune a tutti gas, questa temperatura è la più bassa alla quale
possono essere portati tutti i gas che obbediscono alle leggi sopra indicate.
Infatti un valore di temperatura ancora più basso comporterebbe pressioni negative che sono
fisicamente impossibili.
Pertanto i gas che obbediscono alle leggi sopra indicate per qualsiasi terna di valori (P,V,t)
(gas perfetti), posseggono uno zero fisico di temperatura posto a -273.15 gradi della scala
centigrada.
Detto T0 questo zero fisico, si ha che in T0 è anche P = 0 e pertanto:
0 = P0 (1 + t)
ed essendo P0 0 deve essere :
(1 + t) = 0
;
= - 1/t = - 1/(-273,15) = 0.00366100 [°C-1]
La relazione di Gay-Lussac può scriversi:
t
T
t 273,15
P( t ) P0 1
P0
P0
273,15
T0
273,15
indicando con T = t + 273,15 la “Temperatura del gas perfetto”
Scala del Gas Perfetto:
-
Sostanza termometrica : gas perfetto
Zero fisico a -273,15 °C
Grandezza caratteristica P (a V = costante) o V (a P = costante)
Relazione termometrica : PV = CT (a P o a V costante)
Ampiezza del grado = 1°Celsius (per convenzione)
E’ importante sottolineare che le relazioni P(T)V=cost e V(T)P=cost sono lineari, pertanto due
termometri a gas perfetto (qualsiasi gas perfetto) tarati sugli stessi due punti (qualsiasi) della scala
termometrica (p.es. a 0 °C ed a 100 °C) forniscono misure identiche anche su tutti gli altri punti
della scala.
Equazione del Gas Perfetto
Poiché per un sistema (P,V,T) ciascuna delle variabili di stato può essere scritta in funzione delle
altre due, p.es V = V(P,T)solo , il differenziale di V fatto rispetto a P e T, sarà un differenziale esatto
o totale.
V
V
dV
dP
dT
P T
T P
Le derivate parziali esprimono rispettivamente la legge di Boyle e quella di Charles:
V
V
P
P T
Boyle ) PV CT
Charles ) V
dV
ln V ln P ln T Cost
V
V
dP dT
P
T
V
V
T P T
CT
P
;
dV
dP dT
V
P
T
passando ai numeri si ha : P
V
C' che può scriversi
T
P
V
GR '
T
“mettendo in evidenza” il peso (o la massa ) G del gas e chiamando R’ la costante che raccoglie le
particolari proprietà del gas.
La relazione di stato f(P,V,T)=0 del gas perfetto può essere scritta:
-
PV = R’GT
PV = n R’ Mol T
Pv = R’ T
essendo G = n° di Moli · Peso molecolare (espresso in kg)
utilizzando il volume specifico v = V/G
Se prendiamo in considerazione n = 1 Mole di un gas perfetto (p.es. Aria, Mol = 28,9 kg;
Carbonio12, Mol = 12,00 kg [esatti per definizione]), il volume V sarà il volume occupato da 1
Mole, ossia il suo volume molare. Per due gas perfetti diversi si avrà:
Per il gas a)
PaVmola = Ra’ Mola Ta
Per il gas b)
PbVmolb = Rb’ Molb Tb
Ponendoci nelle stesse (qualsiasi) condizioni di temperatura e pressione, secondo la legge di
Avogadro anche i volume molari dei due gas sono eguali, pertanto:
Ra’ Mola = Rb’ Molb = R (costante dei gas)
La relazione di stato f(P,V,T) = 0 del gas perfetto può essere quindi scritta:
-
PV = n R T
Pv = T R/Mol
utilizzando il volume specifico
Resta infine da calcolare il valore numerico della costante dei gas R
Poiché è noto che, nelle Condizioni Normali (C.N.)
T0 = 0 °C 273,15 (gradi della scala del g.p.)
P0 = 1 Atmf 10330 kg/m2 101325 Newton/m2 (Pascal)
-
e che il volume occupato da 1 Mole di qualsiasi gas è pari a Vmol0 = 22,414 m3,
essendo R = P0Vmol0 / T0 si ha:
-
R = 8314,4
R = 1,98
R = 848
Joules/K (1 Mole)
kcal/°C (1 Mole)
kgm/°C (1 Mole)
Superficie di stato di un gas perfetto
(nel sistema SI)
Coefficienti elastici
Isobara
Superficie di stato
P,V,T
di un Gas perfetto
Isocora
Isoterma
La figura mostra una sezione della superficie di stato di un generico Gas Perfetto; intersecando la
superficie con un piano a temperatura costante si ottengono le linee isoterme che sono iperboli
(equilatere se gli assi P e V hanno la stessa scala) in conformità con l’equazione di Boyle, mentre
le tracce di intersezione dei piani a T costante e P costante sono linee rette come richiesto dalle
equazioni di Charles e di Gay-Lussac.
’
’
A
’
Scelto un punto qualsiasi A, è facile vedere che le tangenti degli angoli ’ e ’ formati dalle
isobare e dalle isocore con la linea parallela all’asse delle temperature esprimono rispettivamente :
P
tan '
T V
V
tan '
T P
= la variazione di pressione per variazione unitaria di temperatura a V costante
= la variazione di volume per variazione unitaria di temperatura a P costante
Infine, tracciata la tangente in A alla generica isoterma e detto ’ l’angolo formato con l’asse della
Pressione, si ottiene:
V
tan ' = la variazione di volume per variazione unitaria di pressione a T costante.
P T
Il segno – è dovuto al fatto che un sistema meccanicamente stabile (come si vedrà meglio in
seguito) non può espandersi quando è soggetto a compressione isoterma.
Per rendere indipendenti dalle dimensioni del sistema i valori delle derivate parziali, esse si
dividono per il volume che il sistema ha in A, mentre la terza derivata viene divisa per la pressione;
si ha pertanto:
1 V
= Coefficiente di comprimibilità isotermo
V P T
1 P
V = Coefficiente di tensione isometrico
P T V
1 V
p
= Coefficiente di espansione isobaro
V T P
t
E’ evidente che, per i gas perfetti, i coefficienti elastici possono essere calcolati facilmente
attraverso le derivate parziali, ottenendo:
V = 1/T
p = 1/T
T = 1/P
Per i gas reali, che non seguono l’equazione del gas perfetto, la determinazione
sperimentale dei coefficienti elastici fornisce un legame tra le variabili di stato che
può sostituire (nell’ambito dei valori P,V,T sperimentati) quello (del tutto generale)
che è fornito dall’equazione di stato.
Alcuni dei coefficienti elastici possono però risultare difficili da misurare in
determinate condizioni sperimentali, per questo è necessario ricavare le relazioni
mutue tra i coefficienti elastici.
Relazioni tra i coefficienti elastici
Come si è detto, per un sistema (P,V,T) può essere scritto il differenziale esatto di ciascuna delle
variabili di stato in funzione delle altre due:
V
V
dV
dP
dT
P T
T P
P
P
dP
dV dT
V T
T V
Che può scriversi
V
V
dV
dP
dT 0
P T
T P
P
dV
V T
P
dP dT 0
T V
Poiché le due equazioni, pur essendo formalmente diverse, esprimono la stessa relazione P,V,T esse
sono identiche ed i coefficienti omologhi devono essere eguali o proporzionali.
Non essendo evidentemente eguali, dovrà sussistere le seguenti proporzionalità:
P
V T
1
1
V
P T
P
T V
V
T P
Da cui possono trarsi alcune interessanti conseguenze:
a)
P
V T
b)
P
V T
c)
P V T
1
T V P T V P
1
V
P T
P T
T V V P
(Teorema di reciprocità)
Queste relazioni (e tutte le altre che si possono ottenere permutando opportunamente le tre variabili
di stato), consentono di calcolare i coefficienti elastici che sono più difficili da valutare
sperimentalmente, come per esempio quelli a Volume costante.
L’ultima relazione mostra infatti come ciascun coefficiente può essere ottenuto dagli altri due:
P V T = p