APPUNTI SECONDA LEZIONE DELLA PROFESSORESSA

APPUNTI SECONDA LEZIONE DELLA PROFESSORESSA MONTAGNA
definizione “semplice” (linguaggio comune):
R = legame, rapporto tra 2 gruppi A e B di oggetti.
RELAZIONE
definizione rigorosa: R = (A, B, G)
dove G = qualunque sottoinsieme del prod. cart. A x B
Prodotto cartesiano: definizione e diversi modi per rappresentarlo.
Coppia ordinata: ci affidiamo alla familiarità dell’espressione. Interessante
comunque analizzare la definizione di Wiener-Kuratowski.
Sottoinsieme: definizione.
Qualche difficoltà quando si considerano sottoinsiemi di un prodotto cartesiano.
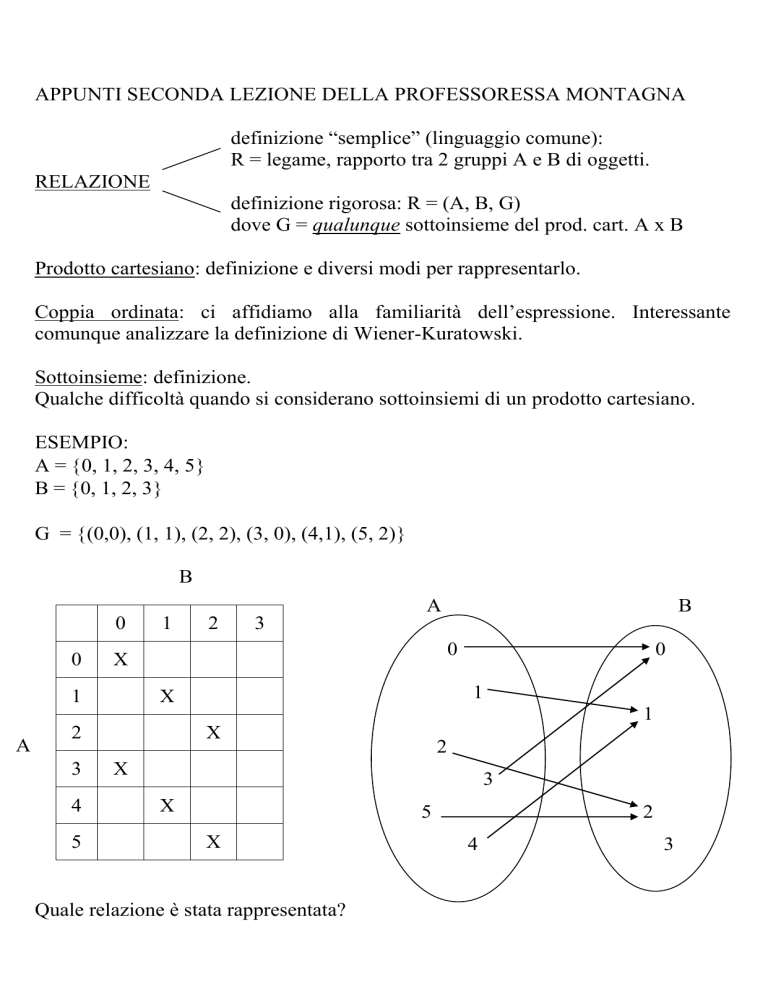
ESEMPIO:
A = 0, 1, 2, 3, 4, 5
B = 0, 1, 2, 3
G = (0,0), (1, 1), (2, 2), (3, 0), (4,1), (5, 2)
B
A
0
0
1
2
3
0
X
1
B
0
1
X
1
A
2
3
4
5
X
2
X
3
X
5
X
Quale relazione è stata rappresentata?
2
4
3
PROPRIETA’ DELLE RELAZIONI
Lavoriamo con relazioni in insiemi numerici (N, Z, Q).
- Riconoscere/scoprire più relazioni tra i numeri di un certo insieme
“arricchisce” l’insieme stesso.
- Le relazioni possono avere o non avere certe proprietà: la verifica della
validità di tali proprietà le rende più interessanti  classificazione (relaz. di
equivalenza, di ordine, …)
FUNZIONE = particolare tipo di relazione f : A  B
Ogni elemento di A è in relazione con uno ed un solo elemento di B.
(Può essere A ≠ B oppure A = B)
 Come si riconosce che una relazione è una funzione (prendendo in esame le varie
rappresentazioni di una relazione)?
ESEMPIO: dati due insiemi A e B determinare diverse funzioni f: A  B
A = 1, 2, 3
B = 1, 2, 3, 4, 6
A B
n  2n
nn+1
n  1 (funzione costante)
n  n (funzione identica)
n6:n
n4–n
…
Trovare esempi di relazioni tra gli stessi insiemi A e B che non risultano essere
funzioni (perché no?)
ESEMPI DI FUNZIONI UNARIE
La relazione del primo esempio proposto è una funzione?
Funzione successivo (considerando N N e Z  Z)
- Concetto primitivo per Peano
- Definizione (dopo aver dato la definizione di insieme totalmente ordinato)
Funzione opposto ( Z  Z)
Funzioni BINARIE: N x N  N
(a, b)  c
ESEMPI: addizione, moltiplicazione, …
La sottrazione è una funzione N x N  N ?
(in realtà non è definita per ogni coppia ordinata (a, b) di N x N… )
E le operazioni di MCD, mcm, elevamento a potenza?
(definizioni, problemi, convenzioni, …)
Tra quali insiemi si possono considerare funzioni?
PROPRIETA’ DELLE FUNZIONI: iniettività, suriettività, biiettività.
- Definizioni
- Come si riconoscono?
- Le funzioni degli esempi visti in precedenza hanno queste proprietà?
RELAZIONI IN UN INSIEME:
A A
Proprietà riflessiva:
- definizione ed osservazioni (uso della scrittura simbolica? Notare il “per
ogni…”)
- come si riconosce questa proprietà nelle diverse rappresentazioni della
relazione?
Analoghe considerazioni per proprietà ariflessiva, antiriflessiva; simmetrica,
antisimmetrica; transitiva; tricotomia.
RELAZIONI DI EQUIVALENZA
ESEMPI
Le seguenti relazioni nell’insieme A quali proprietà hanno?
A
1
2
A
1
3
4
2
A
3
1
2
6
3
Di quali relazioni si tratta?
IL PROBLEMA DELL’AGENTE SEGRETO
Un agente segreto deve introdursi come spia in una base nemica.
Da alcuni informatori ha saputo che all’ingresso gli verrà rivolto un quesito: solo se
saprà rispondere correttamente potrà entrare. Non sapendo quale domanda sarà
posta, la spia decide di piazzare dei microfoni per registrare alcune risposte e
cercare di capire come comportarsi quando si presenterà all’entrata della base.
Arriva il primo personaggio, a cui viene chiesto: “Cosa rispondi se ti dico 12?”
Senza esitazione quello risponde “6” e viene lasciato passare.
Al secondo personaggio che si presenta viene chiesto: “Cosa rispondi se ti dico
10?”
La risposta è “5” e anche costui entra senza problemi.
Per la terza persona la domanda è: “Cosa rispondi se ti dico 8?”
Lei risponde “4” ed entra subito.
Al personaggio successivo viene chiesto: “Cosa rispondi se ti dico 6?”
Alla risposta “3” la porta si apre.
A questo punto l’agente segreto ritiene di aver sentito abbastanza e si presenta
all’ingresso.
Anche per lui la domanda è simile a quella che è stata rivolta agli altri che lo hanno
preceduto: “Cosa rispondi se ti dico 4?”
Senza esitazione risponde…
… “2” e, con sua grande sorpresa, in men che non si dica si ritrova accerchiato e
fatto prigioniero!
… “7” e finalmente può entrare, portando a termine con successo la sua missione.
COME HA RICAVATO LA RISPOSTA CORRETTA?