IL PIANO INCLINATO E L’ATTRITO
Antonio Scafuro – Liceo Scientifico “Rescigno” – Roccapiemonte – Salerno
Roberto Chiumiento – ICT – Università di Salerno
Nello sforzo che facciamo di rappresentare il mondo che ci circonda siamo come quel bambino
che curioso vuol capire come funziona l’orologio appeso alla parete … (Einstein)
Abstract: L’attrito ha aspetti particolarmente importanti e sfuggenti che
cerchiamo di rendere evidenti. Un corpo che striscia su un piano inclinato è
soggetto ad una forza di attrito che in salita ha un verso e in discesa un altro. E
se in salita l’attrito può essere più forte della componente del peso parallela al
piano, non può esserlo in discesa.
Il piano inclinato e l’attrito
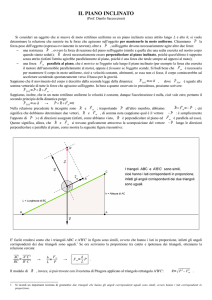
Il moto di un oggetto, A, lungo un piano inclinato, Q, è determinato dalla
componente Px del peso, P, di A parallela a Q e dalla forza di attrito tra Q ed A.
Nel caso in cui il piano sia liscio la risultante delle forze agenti su A è Px,
Figura 1. Px è la risultante se il piano è liscio
Il moto di A è regolato, sia in salita che in discesa, dall’accelerazione costante
a g sen( ) , dove g è l’accelerazione di gravità ed è l’angolo che Q forma
con l’orizzonte. Nel modello che proponiamo, costruito con Cabri Plus, è
possibile fissare i valori di: , g , l , vo ed m e partendo da questi è possibile
calcolare il peso, le sue componenti Px e Py , rispettivamente parallela e
perpendicolare a Q, l’accelerazione e la posizione, x, di A su Q in funzione del
tempo. Supponendo di lanciare A su Q verso l’alto, calcoliamo la velocità
iniziale massima voMax conferibile ad A perché non fuoriesca dal piano. In tal
modo siamo sicuri del ritorno di A. Associato il valore del tempo con la
posizione di un punto t su un vettore T definito ad hoc, servendoci della legge
1
del moto x v0 t a t 2 , leghiamo la posizione di A a quella di t, in modo che
2
animando t vedremo scorrere A su Q, sia in salita che in discesa
Figura 2. Animando t su T vedremo scorrere A su Q
Questo moto di A è un perfetto moto uniformemente accelerato. Se lo
rappresentassimo in un piano XOT vedremmo una parabola caratterizzata
completamente dai parametri del moto. È possibile variare questi e vedere
come cambia la parabola rappresentativa del moto. Ma soprattutto è possibile,
rianimando t, vedere come cambiano il tempo di salita, che comunque è uguale
al tempo di discesa, la distanza percorsa lungo il piano. È possibile notare la
dipendenza dei tempi e delle distanze dai valori di , di vo e di g . È anche
possibile evidenziare l’indipendenza del moto dalla massa di A.
Figura 3. Il moto lungo un piano inclinato liscio è uniformemente accelerato
Se il piano è scabro ed indichiamo con il coefficiente di attrito tra A e Q allora
la situazione diventa alquanto più interessante. Detta Fa la forza di attrito, risulta
Fa Py m g cos( ) e la risultante delle forze agenti su A è: Rs Px Fa
se A sale,
Figura 4 . In salita l'attrito è concorde con Px
Se A scende lungo il piano Rd Px Fa
Figura 5. In discesa Fa e Px sono discordi
Avendo due risultanti diverse, avremo due accelerazioni diverse, quindi due
moti non simmetrici uno dell’altro rispetto al tempo di arresto di A. Infatti, mentre
in salita il moto è regolato dall’accelerazione as g sin cos , in
discesa risulta ad g sin cos
Figura 6. Il grafico del moto di A si compone di due archi di parabole diverse
Variando i parametri che caratterizzano il moto, cioè l’angolo, il coefficiente di
attrito, la velocità iniziale, la lunghezza del piano, la massa di A e perfino il
valore del campo gravitazionale, è possibile osservare come ciascuno di essi
influenzi il fenomeno oggetto di osservazione. In particolare, agendo su o su
è possibile fare in modo che A, arrestatosi dopo la salita, non ritorni giù.
Questo capita quando il modulo di Fa in salita è maggiore o uguale al modulo di
Px. In tal caso, in discesa sarà Fa Px con conseguente risultante nulla ed il
corpo fermo resterà fermo, dovunque esso si trovi
Figura 7. In particolari condizioni A si ferma e non torna giù
www.antonioscafuro.it