Compito del 12 giu 2006

Facoltà di Ingegneria
Prova scritta di Fisica I – 12. 06. 2006
Esercizio n. 1 (Facoltativo per tutti – obbligatorio per Anno di Preparazione. Difficoltà 1)
Un corpo viene lanciato da terra verso l’alto con un angolo =50° rispetto all’orizzontale e con una velocità iniziale di
m
modulo v 0  40 . Trascurando l’attrito dell’aria, calcolare la gittata ed il tempo di volo.
s
1. Il tempo di volo risulta:
y
A. 2.31 s
B. 6.24 s (*)
C. 10.03 s
D. 15.38 s
2.

v0
La gittata risulta:
A. 90 m
B. 120 m
C. 160 m (*)
D. 190 m
=50°
x
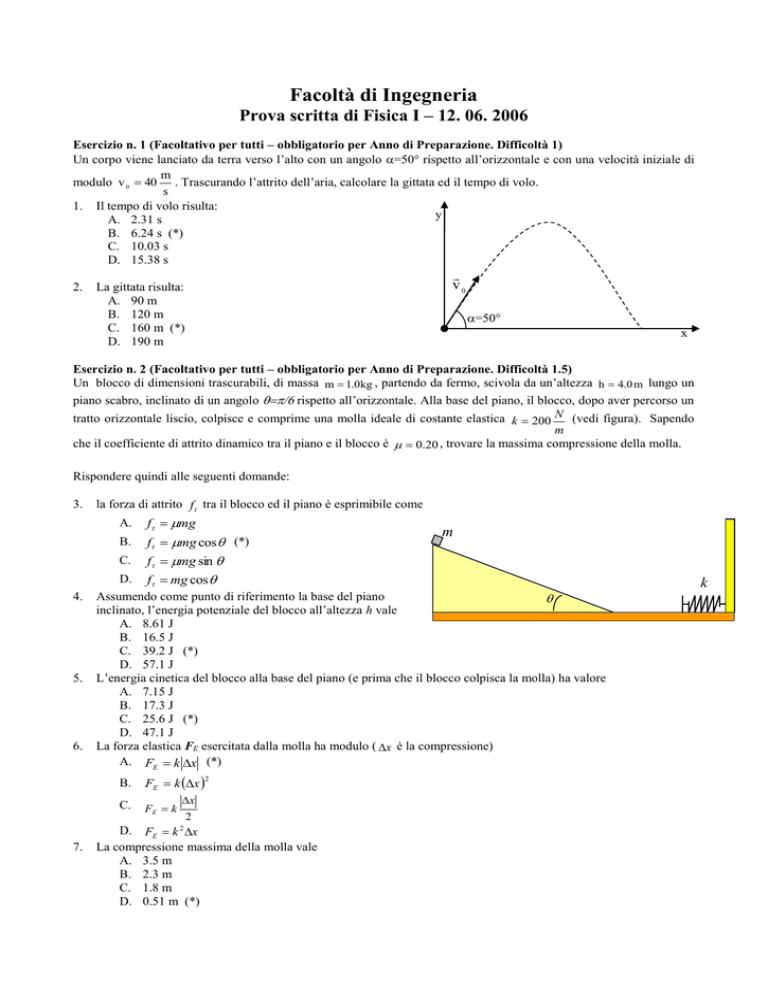
Esercizio n. 2 (Facoltativo per tutti – obbligatorio per Anno di Preparazione. Difficoltà 1.5)
Un blocco di dimensioni trascurabili, di massa m  1.0kg , partendo da fermo, scivola da un’altezza h  4.0 m lungo un
piano scabro, inclinato di un angolo  rispetto all’orizzontale. Alla base del piano, il blocco, dopo aver percorso un
tratto orizzontale liscio, colpisce e comprime una molla ideale di costante elastica k  200 N (vedi figura). Sapendo
m
che il coefficiente di attrito dinamico tra il piano e il blocco è   0.20 , trovare la massima compressione della molla.
Rispondere quindi alle seguenti domande:
3.
4.
5.
6.
7.
la forza di attrito f t tra il blocco ed il piano è esprimibile come
A.
f t  mg
B.
C.
f t  mg cos  (*)
f t  mg sin 
D.
f t  mg cos 
m
Assumendo come punto di riferimento la base del piano

inclinato, l’energia potenziale del blocco all’altezza h vale
A. 8.61 J
B. 16.5 J
C. 39.2 J (*)
D. 57.1 J
L’energia cinetica del blocco alla base del piano (e prima che il blocco colpisca la molla) ha valore
A. 7.15 J
B. 17.3 J
C. 25.6 J (*)
D. 47.1 J
La forza elastica FE esercitata dalla molla ha modulo ( x è la compressione)
A. FE  k x (*)
B.
FE  k x 
C.
FE  k
2
x
2
D. FE  k 2 x
La compressione massima della molla vale
A. 3.5 m
B. 2.3 m
C. 1.8 m
D. 0.51 m (*)
k
Esercizio n. 3 (Facoltativo per tutti. Difficoltà 2)
Un blocco di massa M viene posto su di un piano orizzontale
scabro. Quando al blocco viene collegato, tramite un filo
inestensibile e di massa trascurabile, un pesetto di massa m0, in
modo simile a quanto mostrato nella figura, dove si nota che il
filo viene fatto scorrere su di una carrucola ideale C, il sistema
blocco + pesetto si muove di moto uniforme.
Calcolare il coefficiente di attrito dinamico  tra il blocco e il
piano orizzontale
Successivamente, un pesetto di massa m>m0 viene connesso al
filo e posto, in luogo di quello di massa m0, ad altezza h rispetto
al suolo, così come mostrato nella figura. Il pesetto di massa m
viene lasciato andare con velocità iniziale nulla.
Avendo calcolato il coefficiente di attrito  , determinare
l’accelerazione del pesetto di massa m, il tempo di caduta e la
velocità con cui il pesetto stesso arriva al suolo.
Si considerino il blocco e il pesetto come punti materiali.
Sia M  3.0kg , m  2.0kg , m0  1.0kg , h  0.98m .
Piano orizzontale
scabro
M
C
m(m0)
m
h
Rispondere quindi alle seguenti domande:
8.
il modulo della forza d’attrito agente sul blocco è esprimibile come segue:
A. f t  m0 g
B.
f t  Mg (*)
C.
f t  gh
Mg
ft 
2
D.
9.
il coefficiente di attrito dinamico, ottenuto analizzando il sistema in condizioni di equilibrio, così come spiegato nel
testo, vale
A.   2 g
2
3
1
C.  
(*)
3
g
D.  
3
B.

10. l’accelerazione a del pesetto, ottenuta quando la sua massa è m, vale
A. a  m  M g
mM 3
B. a  m g
mM 3
C. a  m g
mM
m
D. a   M g (*)
mM
11. il tempo di caduta del pesetto vale
A. 1.0 s (*)
B. 2.5 s
C. 25 s
D. 32 s
12. la velocità con la quale il pesetto di massa m arriva al suolo vale
A. 1.96 m/s (*)
B. 17.3 m/s
C. 39.2 m/s
D. 52.4 m/s
Esercizio n. 4 (Facoltativo per tutti. Difficoltà 2.5)
Si consideri il sistema, riportato in figura, costituito da tre corpi di masse mR,
mC e mB. Il corpo di massa mR è un rocchetto cilindrico (cilindro pieno) di
raggio R ed è inizialmente posto nel punto medio di un piano, inclinato di un
angolo  rispetto all’orizzontale e lungo L. Il corpo di massa mC è una carrucola
cilindrica di raggio r libera di ruotare, senza attrito, attorno al proprio asse. Il
corpo di massa mB , infine, funge da contrappeso per il rocchetto ed è collegato a
quest’ultimo mediante un filo inestensibile e di massa trascurabile, che può
avvolgersi sul rocchetto stesso.
Il sistema, lasciato da fermo, evolve in maniera da far scendere il rocchetto sul
piano inclinato con un moto di puro rotolamento.
Calcolare l’accelerazione a di mB e successivamente rispondere alle seguenti
domande.
Sia mR  4.0kg , mC  1.0kg , mB  0.50kg , L  2.0m , r  0.20m ,
R  0.30m ,  
C
mR
mB

 .
6
13. la velocita’ angolare C della carrucola è esprimibile, in termini della velocità V di mB, come:
A.  2  2V
C
r
B. C2  V
r
C.   2V
C
r
D.  C  V (*)
r
14. l’accelerazione a di mB vale:
mR  mB
g
m R  m B  mC
m R sin 
 mB
2
B. a 
g (*)
3
1
m R  m B  mC
8
2
m

m
R
B
C. a 
g
3
1
m R  m B  mC
4
2
m R sin   m B
D. a 
g
m R  m B  mC
A.
mC
a
15. la velocità Vf del contrappeso di massa mB quando il rocchetto è alla base del piano inclinato vale
A. V f  3 gL
8
3g
B. V f 
5L
C. V f  2 gL (*)
5
3
D. V f  gL
4
16. la velocità Vcm del centro di massa del rocchetto quando esso è alla base del piano inclinato vale:
m
A. Vcm  0.312
s
m
B. Vcm  1.40
(*)
s
C. Vcm  2.33 m
s
D. Vcm  3.15 m
s
17. la velocità angolare della carrucola quando il rocchetto è alla base del piano inclinato vale:
A.  C  1.13 rad
s
rad
B.  C  3.31
s
rad
C.  C  14.0
(*)
s
D.  C  19.3 rad
s
Esercizio n. 5
(Facoltativo per tutti, ma fortemente consigliato per Ing. Edile-Architettura. Difficoltà 3)
Per il sistema in figura, in cui le carrucole girano senza attrito (e la molla non è presente), calcolare l’accelerazione a del
corpo 1
Successivamente il corpo 1 viene collegato al pavimento mediante una molla di Hooke (punteggiata in figura) di
rigidezza K. Tenendo presente il risultato precedente scrivere la pulsazione del sistema, dettagliando i passaggi.
18. l’accelerazione a del corpo 1 vale
4M1  4M 2  8M 4 sin 
g (*)
4M1  3M 2  4M 3  12M 4
M  M 2  2M 4 sin 
B. a  1
g
M1  M 2  M 3  M 4
M 1  4M 2  8M 4
C. a 
g
4M 1  3M 2  4M 3  3M 4
A. a 
M3, R3
M4, R4
M2, R2
D. risposta corretta non presente
M1
19. la pulsazione del sistema vale
A.  
2K  M 4  M 1
4M 1  3M 2  4M 3  12M 4
B.

K
M1  M 2  M 3  1M 4
C.

2K
(*)
4M 1  3M 2  4M 3  12M 4
K

D. risposta corretta non presente
Altre domande (facoltativo per tutti)
20. Un blocco scivola su un piano scabro. La forza di attrito compie
A. un lavoro nullo, se il piano è orizzontale
B. un lavoro positivo se il piano è inclinato e il blocco si muove verso il basso
C. un lavoro positivo se il piano è inclinato e il blocco si muove verso l’alto
D. un lavoro negativo, in tutti i casi (*)
21. Una ruota omogenea ha massa M, raggio R e momento d’inerzia I rispetto all’asse passante per il suo CM. Se
la ruota compie un moto di puro rotolamento, con il CM che si sposta con velocità di modulo v CM , l’energia
cinetica della ruota risulta
1
2
Mv CM
2
1
1 I 2
2
Mv CM

v CM (*)
B.
2
2 R2
1 I 2
v CM
C.
2 R2
A.
D.
1
1 2
2
Mv CM
 Iv CM
2
2
22. Il periodo di oscillazione di un pendolo semplice non dipende
A. dall’ampiezza dell’oscillazione (*)
B. dalla lunghezza del filo
C. dalla lunghezza del filo
D. dall’accelerazione di gravità
23. Un moto rettilineo (posizione x, velocità v, accelerazione a) è armonico quando l’accelerazione è
A. a  costante
B. a   kx con k=costante (*)
C. a  kx 2 con k=costante
D. a   kv con k=costante


24. Un punto materiale di massa m ha posizione r rispetto ad un polo O e velocità v . Su di esso agisce una forza

F . Il suo momento angolare rispetto ad O è


A. r  mv (*)
 
B. r  mv
 
C. r  F
 
D. r  F
25. Il teorema di Koenig dell’energia cinetica dice che
A. L’energia cinetica di un sistema di particelle è sempre nulla
B. L’energia cinetica di un sistema di particelle è uguale all’energia cinetica del CM del sistema
C. L’energia cinetica di un sistema di particelle è uguale all’energia cinetica del sistema rispetto al
sistema del centro di massa
D. L’energia cinetica di un sistema di particelle è uguale all’energia cinetica del CM del sistema più
l’energia cinetica del sistema rispetto al sistema del centro di massa (*)
26. Un punto materiale descrive una traiettoria circolare con velocità angolare costante  . Sul punto agisce una
forza
A. nulla perché  è costante
B. proporzionale ad 
C. inversamente proporzionale ad 
27.
28.
29.
30.
31.
D. proporzionale ad  2 (*)
In un urto anelastico si conserva:
A. La quantità di moto (*)
B. L’energia cinetica
C. L’energia meccanica
D. Nessuna grandezza fisica
Un blocchetto viene calato in un pozzo di 10 m di profondità. La forza di gravità compie un lavoro
complessivo
A. Nullo
B. Positivo (*)
C. Negativo
D. Di segno dipendente dal cammino seguito
Un sasso viene lanciato orizzontalmente da una torre. Il suo moto è
A. uniforme in direzione orizzontale ed uniformemente accelerato in direzione verticale (*)
B. uniformemente accelerato in direzione orizzontale ed uniforme in direzione verticale
C. uniformemente accelerato sia in direzione orizzontale che verticale
D. uniforme sia in direzione orizzontale che verticale
Un punto materiale che si muove descrivendo una traiettoria circolare può avere
A. accelerazione normale nulla ed accelerazione tangenziale diversa da zero (*)
B. accelerazione normale diversa da zero ed accelerazione tangenziale nulla
C. accelerazione normale ed accelerazione tangenziale nulle
D. accelerazione normale ed accelerazione tangenziale parallele tra loro
Un punto materiale si muove lungo l’asse x (moto rettilineo) con velocità v  0 ed accelerazione costante
a  0 . Il modulo della velocità
A. rimane costante nel tempo
B. aumenta al passare del tempo (moto accelerato) (*)
C. diminuisce al passare del tempo (moto decelerato)
D. prima aumenta poi diminuisce
m
m
con k  2 2 . Al tempo
s
s
t=0 si trova nella posizione x o  xt  0  10 m . Al tempo t=2s si trova nella posizione
A. x  8m
B. x  10 m
C. x  12m
D. x  14m (*)
33. Nel moto parabolico di un proiettile lanciato verso l’alto ad un angolo di 45°, nel punto di altezza massima, la
velocità ha
A. componente orizzontale nulla e componente verticale diversa da zero
B. componente orizzontale diversa da zero e componente verticale nulla (*)
C. entrambe le componenti nulle
D. entrambe le componenti diverse da zero
 
34. Siano a e b due vettori e sia  l’angolo tra di essi. Il modulo della somma vale
32. Un punto materiale si muove di moto rettilineo lungo l’asse x con velocità v  kt
A.
a 2  b 2  2ab cos 
B.
a 2  b 2  2ab cos  (*)
a 2  b2
C.
D. a  b
35. La quantità di moto totale di un sistema si conserva quando
A. la risultante delle forze interne è nulla
B. la risultante delle forze esterne è nulla (*)
C. la risultante delle forze interne è uguale alla risultante delle forze esterne
D. la risultante delle forze interne è uguale ed opposta alla risultante delle forze esterne
Domande di Acustica per Ing. Edile-Architettura
36. Quale e’ sbagliato ?
A. L w = 10 Log( W/ Wo )
B. L I = 10 Log( I / Io )
C. L p = 10 Log( P / Po ) (*)
D. nessuno
37. Ricordando che i valori di riferimento sono: p0 = 20 µPa = 2 × 10-5 Pa, I0 = 10-12 W/m2 , quanto vale il livello
di intensita’ sonora corrispondente ad una intensita’ di 1 W/m2 ?.
A. 10 dB
B. 100 dB
C. 120 dB (*)
D. 12 dB
38. L’intensita’ sonora e’ proporzionale a:
A. pressione
B. quadrato della pressione (*)
C. campo elettrostatico
D. cubo della potenza
39. Al fattore di direttivita’ Q=8 corrisponde una emissione in:
A. un semispazio
B. un quadrante
C. un sestante
D. un ottante (*)
40. Il tempo di riverbero, secondo Sabine, e’ pari a:
A. T=0.16 Vol / Assorb (*)
B. T=0.16 Assorb / Vol
C. T=0.16 Vol^2 / Riflessione
D. nessuna delle precedenti
Q
4

) e’ valida:
41. La formula L p  L W  10 Log (
2
RL
4πr
A.
B.
C.
D.
in ambiente esterno
in ambiente anecoico
in ambiente interno (*)
e’ sbagliata.
42. La formula L p  L W  10 Log(Q)  20 Log(r) 11 dB e’ valida:
A. in ambiente esterno (*)
B. in ambiente anecoico
C. in ambiente interno
D. e’ sbagliata
43. Le curve isofoniche evidenziano una maggiore sensibilita’ dell’orecchio umano nell’intervallo:
A. 2-20 Hz
B. 100-500 Hz
C. 2- 5 KHz (*)
D. 15- 20 KHz
44. Nell’acustica architettonica si usa prevelentemente la curva di ponderazione:
A. A (*)
B. B
C. C
D. D
45. Per la presenza di componenti tonali in una emissione sonora la normativa prevede una penalizzazione del
livello di pressione di:
A. - 3 dBC
B. +3 dBA (*)
C. +5 dB
D. 0 dBA
Soluzione
Esercizio n. 2
La forza di attrito f t tra il blocco e il piano è esprimibile come segue
f t  mg cos   1.697 N .
Rispetto alla base del piano inclinato, l’energia potenziale del blocco vale
U  A  mgh  39.2J .
L’energia cinetica KB del blocco alla base del piano (e prima che il blocco colpisca la molla) si trova scrivendo
K B  U  A   f t L .
Pertanto si ha
K B  U  A  f t L  25.6J .
La forza elastica FE esercitata dalla molla ha modulo pari a
FE  k x .
Alla base della guida, il blocco possiede un’energia cinetica pari a KB. Mentre il blocco comprime la molla, questa
energia cinetica si trasforma in energia potenziale elastica della molla e la trasformazione è completa quando la molla è
compressa al massimo. Quindi:
KB 
2K B
1
kx 2  x 
 0.51m
2
k
dove x qui rappresenta la compressione massima della molla.
Esercizio n.3
La forza di attrito sul blocco si esprime come segue
f t  Mg .
Quando il sistema è all’equilibrio si ha
T  f t  m0 g ;
pertanto, ponendo f t  Mg , otteniamo
m0 1 .

M 3

L’accelerazione del pesetto si trova scrivendo le equazioni del moto seguenti:
T  f t  Ma

 N  Mg  0
(blocco)
mg  T  ma
(pesetto).
Aggiungendo alle equazioni di sopra la legge fenomenologia f t  N  Mg e risolvendo per a, si ottiene
a
g
m  M
g .
mM
5
Per ottenere la velocità con la quale il pesetto di massa m arriva al suolo si pone
2 gh
m
 1.96
5
s
V f2  2ah  V f 
Infine, il tempo di caduta del pesetto si ottiene scrivendo
tf 
Vf
a
 1.0s .
Esercizio n. 4
La velocita’ angolare C della carrucola è esprimibile, in termini della velocità V di mB, come segue
V
  .
C
r
Si può calcolare l’accelerazione a di mB scrivendo, per la conservazione dell’energia meccanica
K f  U i   U  f  
13
11
1
 m sin 

2 2
2 2
2
 mB  gy
 mR R R   mC r C  mBV   R
22
22
2
2




ove y è la quota alla quale sale il blocco di massa mB rispetto alla sua posizione iniziale e R è la velocità angolare del
rocchetto. Imponendo adesso il vincolo cinematico
V  2R R  C r
si ottiene, risolvendo per V2,
 mR sin 
 mB

2
V 2  2
 3 mR  1 mC  mB
2
 8
In questo modo, scriviamo:

 .
g y


mR sin 
 mB
2 .
2
a
g g
3
1
5
mR  mC  mB
8
2
Pertanto, si ha
2  L
V f2  2 g   V f 
5  2
2
gL .
5
la velocità Vcm del centro di massa del rocchetto quando esso è alla base del piano inclinato vale
Vf
m
V 
 1.40 .
cm
2
s
la velocità angolare della carrucola quando il rocchetto è alla base del piano inclinato vale
C 
Vf
r
 14.0
rad .
s