4. DISPOSITIVI A SEMICONDUTTORE
Sui materiali semiconduttori è basata la maggior parte dei dispositivi attivi di uso elettronico. I
materiali semiconduttori più noti sono il Germanio (Ge), il (Si) e l’Arseniuro di Gallio (GaAs). Non
considerando dispositivi particolari, il Germanio è stato il primo materiale usato in modo organico
per la costruzione di dispositivi elettronici. Oggi la maggior parte dei dispositivi elettronici impiega
il Silicio. L’Arseniuro di Gallio è il capostipite di una classe di semiconduttori, detti III - V dalla
colonna di appartenenza alla tabella periodica degli elementi dei singoli elementi costituenti. Sui
semiconduttori III - V si basano dispositivi ultraveloci e tutti quei dispositivi destinati agli impieghi
di tipo ottico-elettronico, come i Led, o i laser a semiconduttori impiegati per la trasmissione dei
segnali in fibra ottica. I semiconduttori sono comunque una categoria molto vasta di materiali,
alcuni noti e sporadicamente usati in elettronica prima o indipendentemente dallo sviluppo dei
transistori (esempio fotoresistenze al Solfuro di Cadmio, termistori ecc.), alcuni di sviluppo molto
recente, come ad es. i semiconduttori II - VI usati fra l’altro per la rivelazione di radiazione
infrarossa.
In generale i dispositivi a semiconduttore usati in elettronica (almeno quelli di cui ci occuperemo)
sono ottenuti da materiali con struttura monocristallina. Per il loro studio è quindi essenziale partire
dai fenomeni che si verificano nella materia in una struttura monocristallina.
4.1. METALLI ISOLANTI SEMICONDUTTORI
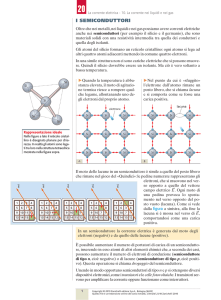
Gli elettroni in un atomo occupano ben determinati livelli discreti di energia. Prendiamo in
considerazione gli elettroni di valenza, ai quali si devono i fenomeni di conduzione, e supponiamo,
come accade nel Germanio e nel Silicio, che ognuno dei quattro elettroni di valenza possa occupare
due livelli di energia, che corrispondono alla situazione di elettrone vincolato nel legame oppure
libero. In un cristallo, a causa dell’interazione tra atomi vicini, entra in gioco il principio di
esclusione di Pauli: gli elettroni dei vari atomi non possono più stare sugli stessi livelli e si
distribuiscono quindi ognuno su un livello distinto. Si può pensare che, man mano che la distanza
interatomica si riduce a quella propria del reticolo cristallino, i livelli elettronici dell’atomo isolato
formino, a causa del grande numero di elettroni nel cristallo, delle bande continue di energia
permessa. Queste bande possono rimanere distinte, separate da una banda vietata, che quindi non
contiene livelli permessi, oppure possono risultare parzialmente sovrapposte. Quando i livelli
corrispondenti a elettroni vincolati e elettroni liberi degenerano in bande danno luogo a due bande
permesse. Nella banda inferiore, detta di valenza, tutti i livelli disponibili risultano occupati da
elettroni; questi risultano quindi vincolati, non possono contribuire alla conducibilità elettrica del
materiale. Nella banda superiore che si dice di conduzione, i livelli permessi sono liberi e possono
venire occupati da elettroni in grado di trasportare una corrente elettrica. Un elettrone, per potersi
muovere e quindi contribuire al trasporto di corrente, deve quindi prima passare dalla banda di
energia
livelli originari
atomo singolo
distanza interatomica
livelli degenerati
in bande in un
cristallo
Fig.1: Degenerazione al
ridursi della distanza
interatomica dei livelli di
energia che l’elettrone
può occupare in un atomo
isolato.
valenza, dove è vincolato, a quella di conduzione. A questo punto si possono distinguere tre
situazioni (fig.2), che danno origine a tre categorie di materiali.
La banda di conduzione e quella di valenza sono separate da un intervallo di energia EG- energia
della banda vietata o “gap”- di parecchi elettronvolt. Il materiale in questione è allora un isolante,
perché in condizione normali di temperatura e a meno di forti sollecitazioni elettriche gli elettroni
non possono passare in banda di conduzione e quindi il materiale non conduce la corrente elettrica.
E’ questo il caso ad esempio dei più comuni materiali isolanti usati nella microelettronica, come il
biossido di silicio (SiO2) in cui la banda vietata è di circa 8 ev o il nitruro di silicio (Si3N4) con un
gap di circa 4 ev.
banda di conduzione
banda di
conduzione
elettroni liberi
EG 6 ev
banda proibita
EG 1 ev
lacune
banda di valenza
banda di
valenza
Fig.2: Modello di banda di isolanti, semiconduttori, metalli.
La banda di conduzione e quella di valenza sono parzialmente sovrapposte. In questo caso basta
un piccolo campo elettrico applicato perché gli elettroni acquisiscano un’energia addizionale
sufficiente a “liberarli” portandoli nella banda di conduzione. Un tale materiale è un conduttore.
Questa è la situazione tipica nei metalli.
La banda di conduzione e quella di valenza sono separate da un intervallo di energia piccolo,
dell’ordine di 1 ev. In questo caso il materiale è un semiconduttore. Ad esempio a 0 K nel Ge la
banda proibita è di 0,785 ev e di 1,12 ev nel Si.
4.2. IL FENOMENO DELLA CONDUZIONE NEI SEMICONDUTTORI
Fig.3: Struttura cristallina del Silicio.
A basse temperature i semiconduttori si comportano da isolanti, perché gli elettroni degli atomi
sono vincolati nei legami chimici con gli atomi vicini, almeno per campi elettrici applicati che non
siano in grado di portare gli elettroni dalla banda di valenza a quella di conduzione. Tuttavia
all’aumentare della temperatura si riduce la stabilità dei legami e quindi una certa quantità di
elettroni acquista energia sufficiente per passare nella banda di conduzione.
Il semiconduttore più usato è il Silicio, un elemento appartenente alla quarta colonna della tabella
periodica. La fig.3 rappresenta la sua struttura cristallina. Si tratta di una struttura a diamante, con
cella elementare cubica a facce centrate. Ogni atomo di Silicio scambia ognuno dei quattro elettroni
dell’orbita esterna con gli atomi vicini, formando quattro legami covalenti. La simmetria della
struttura cristallina spiega l’isotropia delle caratteristiche chimico-fisiche di questo materiale, che
così possono essere rappresentate con grandezze scalari.
4.2.1. Elettroni e lacune
Gli elettroni che sono passati nella banda di conduzione lasciano poi dei livelli liberi nella banda di
valenza. La mancanza di elettroni nella banda di valenza si dice lacuna. Sia gli elettroni nella banda
di conduzione che le lacune nella banda di valenza possono contribuire alla conduzione di corrente
elettrica. Un semiconduttore in cui le lacune nella banda di valenza sono in numero uguale agli
elettroni in banda di conduzione si dice intrinseco. Esistono dei metodi (drogaggio), per far sì che
la conducibilità di un semiconduttore sia dovuta prevalentemente a portatori di carica di un solo
tipo.
La lacuna si comporta a tutti gli effetti come una particella di carica positiva, che si muove in verso
opposto a quello degli elettroni. Un semiconduttore in cui la conduzione è dovuta prevalentemente a
lacune si dice di tipo p; uno in cui la conduzione è dovuta prevalentemente a elettroni si dice di tipo
n.
Semiconduttori di questo genere si dicono estrinseci. Poiché l’energia della banda proibita in un
cristallo è funzione della distanza interatomica, EG dipende dalla temperatura. Ad esempio nel
Silicio a 300 K EG si riduce a 1,1 ev.
4.2.2. Livello di Fermi
La distribuzione degli elettroni nei livelli permessi si ricava dalla statistica quantistica ed è descritta
dalla funzione di Fermi - Dirac che definisce la probabilità P(E) di occupazione da parte di un
elettrone del livello di energia di valore E.
1
P( E )
EE F
1
e
kT
dove k è la costante di Boltzmann uguale a 0,86 10-4 ev/grado Kelvin, T la temperatura assoluta in
gradi K e EF è un livello di energia detto livello di Fermi.
Da un’analisi della P(E) risulta che a 0 K tutti i livelli di energia superiori a EF sono liberi e tutti i
livelli inferiori sono occupati. Si dice che il livello di Fermi rappresenta la massima energia che un
elettrone può avere allo zero assoluto.
I livelli permessi inferiori a EF costituiscono la banda di valenza, quelli superiori la banda di
conduzione. Negli isolanti e nei semiconduttori EF cade entro una banda vietata, nei metalli taglia
invece una banda permessa. Si capisce ora, sempre dall’esame della P(E) (fig.4), che nel caso dei
semi-conduttori, a causa del valore non elevato del gap, anche a temperatura non molto elevata, es.
alla temperatura ambiente, esiste una probabilità non nulla di trovare elettroni in banda di
conduzione (e lacune in banda di valenza).
Si dimostra che nei semiconduttori intrinseci il livello di Fermi cade all’incirca a metà della banda
vietata.
E
banda permessa
T=300 K
EC
banda vietata
T=0K
EF
EV
banda permessa
0
0,5
1
P(E)
Fig.4: Andamento della probabilità di occupazione allo zero assoluto e a
temperatura ambiente.
4.2.3. Drogaggio
Come già accennato la conducibilità di un semiconduttore può venire modificata. A questo scopo si
aggiungono al semiconduttore opportuni materiali, detti droganti, i cui atomi si comportano da
impurità sostituzionali, cioè prendono il posto di un atomo del materiale base nel reticolo cristallino
di questo. Nel caso del Germanio e del Silicio, che sono tetravalenti, l’aggiunta di materiali
pentavalenti, detti donatori, come Fosforo (P), Arsenico (AS), Antimonio (Sb), rende disponibile,
per ogni atomo di drogante, un elettrone quasi libero, dal momento che, dei cinque elettroni
periferici del drogante, solo quattro possono venire legati con gli atomi circostanti. Si dice in questo
caso che si è effettuato un drogaggio di tipo n. All’elettrone libero resta associato uno ione positivo,
che costituisce una carica fissa. Analogamente, se si aggiungono al semiconduttore dei materiali
trivalenti detti accettori, come Boro (B), Indio (In), Alluminio (Al), l’impurità che si inserisce nel
reticolo cristallino tende a catturare un elettrone agli atomi circostanti, diventando uno ione carico
negativamente e mettendo in circolazione una lacuna. Un semiconduttore drogato in questo modo si
dice drogato p. I livelli di drogaggio, cioè il numero di impurità aggiunto, sono molto piccoli.
Nel seguito faremo riferimento quasi esclusivamente al Silicio. Mentre il Silicio contiene 1022
atomi/cm3, il numero di droganti varia generalmente tra 1014 e 1019. I livelli energetici introdotti dai
droganti nel modello di banda non subiscono gli effetti del principio di esclusione. Nel Silicio n si
ha quindi l’introduzione di un livello in più nella banda vietata, prossimo al limite inferiore della
banda di conduzione (basta infatti un’energia molto piccola per es. quella fornita alle particelle a
temperatura ambiente, perché l’elettrone, poco legato, passi in banda di conduzione) e nel
semiconduttore p si ha l’introduzione di un livello nella banda vietata, prossimo al limite superiore
della banda di valenza. Il livello di Fermi per la sua stessa definizione, si sposta verso l’alto nei
semiconduttori drogati n e verso il basso nei semiconduttori drogati p. Infatti a parità di temperatura
il drogaggio n rende molto più grande la probabilità di presenza di elettroni nei livelli superiori a
quello di Fermi. Si dimostra che lo spostamento è dato, nell’ipotesi generalmente accettabile di
completa ionizzazione del drogante, cioè che ogni atomo drogante fornisca un elettrone o una
lacuna, da
EF = EF - EFi = kTln(N/ni),
n
p
EC
EF
EF
EFi
EF
EV
EF
Fig.5: Spostamento del livello di Fermi nel semiconduttore drogato
dove EFi è il livello di Fermi nell’intrinseco, N la concentrazione netta di donatori o accettori, cioè
la differenza tra il numero di donatori e quello di accettori inseriti nel materiale, presa comunque
con il segno positivo, ni il numero di elettroni nel Silicio intrinseco, che vale a 300 K, 1,45 1010
cm-3. La fig.5 mostra lo spostamento del livello di Fermi nel semiconduttore drogato.
Sempre nell’ipotesi di completa ionizzazione del drogante la concentrazione n di elettroni nel
semiconduttore drogato n coincide con il numero netto dei donatori, mentre la concentrazione p nei
semiconduttori drogati p coincide con il numero netto degli accettori. Le concentrazioni n degli
elettroni e p delle lacune in un semiconduttore estrinseco in equilibrio termico (per equilibrio
termico si intende l’assenza di ogni sollecitazione imposta dall’esterno sulle popolazioni dei
portatori di carica) sono legate allo spostamento del livello di Fermi dalle relazioni
n ni
E F
e kT
p ni
E F
e kT
In situazioni di equilibrio vale dunque la legge
np = ni2
La formula precedente mostra come al crescere di n diminuisce p e viceversa. Nel semiconduttore n
si dice che gli elettroni sono i portatori di maggioranza, mentre le lacune sono i portatori di
maggioranza nel semiconduttore drogato p.
Se il drogaggio è molto elevato, 1019 o più, il semiconduttore diviene degenere, cioè praticamente
un conduttore, e il livello di Fermi taglia una delle bande permesse. In questo caso l’ipotesi di
completa ionizzazione del drogante può non essere più accettabile.
4.2.4. Correnti di conduzione e di diffusione
La corrente totale che percorre un semiconduttore è dovuta sia al movimento degli elettroni che
delle lacune. Ognuno dei due tipi di portatori subisce sia un movimento di tipo conduttivo, dovuto
alla presenza di campi elettrici, sia uno di tipo diffusivo dovuto al gradiente di concentrazione. In
generale la densità di corrente J in un semiconduttore si può esprimere come
J q( n n p p ) E q( Dn
n
p
Dp
)
x
x
q è la carica dell’elettrone, n e p le mobilità degli elettroni e delle lacune, Dn e Dp le costanti di
diffusione, sempre di elettroni e lacune, E il campo elettrico.
Il primo membro rappresenta la corrente di conduzione, come somma delle due componenti, di
elettroni e lacune, il secondo membro è la corrente di diffusione. La diffusione avviene in senso
opposto al gradiente di concentrazione, cioè dalla concentrazione maggiore verso la concentrazione
minore. Questo spiega i segni che compaiono nell’espressione della corrente. La mobilità, in
generale diversa per gli elettroni e le lacune è definita come il rapporto tra velocità assunta dalle
particelle e campo elettrico. La mobilità decresce all’aumentare della temperatura e del drogaggio.
Mobilità e costante di diffusione sono legate dalle relazione di Einstein
D
kT
q
In assenza di campi elettrici la corrente si riduce alla sola componente diffusiva, in assenza di
gradienti di concentrazione alla sola componente conduttiva. Nel caso in cui il semiconduttore sia
di tipo p o di tipo n la corrente di conduzione si riduce praticamente a quella dei soli portatori di
maggioranza.
Dall’espressione della corrente di conduzione,
J q( n n p p ) E E
si definisce la conducibilità del materiale.
Il drogaggio altera la conducibilità di un semiconduttore, che, note le mobilità, può essere calcolata
dalle espressioni delle concentrazioni dei portatori. Il modo più pratico per ottenere la conducibilità
di un semiconduttore drogato è tuttavia quello di ricorrere alle curve di Irvin, riportate in fig 6, che
forniscono in forma grafica la conducibilità del semiconduttore in funzione del drogaggio per
semiconduttori di tipo p o di tipo n.
Viene anche riportata una tabella con le più importanti caratteristiche chimico fisiche dei principali
materiali usati nell’elettronica dello stato solido.
Notiamo infine come il valore della mobilità sia molto diverso nei diversi semiconduttori usati in
elettronica. In particolare l’altissima mobilità degli elettroni nell’Arseniuro di Gallio giustifica
l’impiego di questo materiale per la costruzione di dispositivi ultraveloci.
Fig.6: Curve di Irvin, che forniscono la resistività di Silicio drogato p o n in funzione del drogaggio.
4.3. EFFETTO HALL
Questo effetto dimostra l’esistenza nei semiconduttori di una conducibilità di tipo p e di tipo n,
consente di misurare la conducibilità e la mobilità dei portatori e costituisce il fenomeno su cui si
base il funzionamento delle magnetoresistenze e dei generatori di Hall, componenti impiegati
rispettivamente come sensori e per la misura di campi magnetici.
Consideriamo una lastrina di materiale semiconduttore, fig.7, percorsa da una corrente I e sottoposta
_
a un campo magnetico B . I portatori di carica che si muovono entro il materiale con velocità
_
v subiscono la forza di Lorentz data da
_
_
_
F q v B
(1)
_
dove q è la carica (con segno) della particella. Per effetto della forza F sia le particelle positive
(lacune), che quelle negative (elettroni) si addensano dallo stesso lato della piastrina. Infatti se la
corrente è dovuta a lacune, la (1) si scrive:
_
_
_
F q v B
dove q e v sono prese con il segno positivo. Se la corrente è dovuta a elettroni la (1) diventa, poiché
la velocità delle particelle in questo caso ha verso opposto a quello della corrente I
_
_
_
F q( v ) B
B
F
cioè la forza che agisce sia sugli elettroni che sulle lacune ha la
stessa direzione, quindi spinge le particelle dei due tipi dallo stesso
lato della piastrina. Quindi se la conduzione è dovuta a elettroni
d
I
un lato della piastrina si carica negativamente, mentre se è dovuta
w
a lacune lo stesso lato si carica positivamente. A un certo punto si
Fig.7: Piastrina di semicon- arriva a una situazione di equilibrio in cui la tensione Vh prodotta
duttore sottoposta a campo impedisce l’accumulo di ulteriori cariche. In questa situazione il
campo elettrico prodotto dalle cariche accumulate esercita una
magnetico
forza che bilancia la forza di Lorentz:
V
Eq h q qvB
d
(2)
La velocità dei portatori è legata alla densità di corrente J da:
J
I
nqv v
wd
(3)
dove con si indica la densità di carica e n è il numero di portatori per unità di volume.
Ricavando v dalla (3) e sostituendola nella (2) si ha
Vh
IB
vB
d
wd
e quindi
Vh
BI
w
Dal segno di Vh si ricava il tipo di semiconduttore. Dal suo valore, noti B, I, w si ricava e dalla
nq la densità dei portatori di carica. Inoltre, misurando con altri metodi la conducibilità =,
si ottiene la mobilità .
4.4. LA GIUNZIONE P-N
Se una zona di semiconduttore drogato n viene posta a contatto con una zona drogata p (in realtà il
contatto è a livello atomico e le due zone sono prodotte insieme in un unico monocristallo), si
produce una struttura elementare detta giunzione p-n. Le lacune dalla zona p diffondono nella zona
n, gli elettroni dalla zona n in quella p. Si ha quindi una ricombinaziome di cariche mobili, che
lascia scoperta una zona di cariche fisse, detta zona di svuotamento, ai due lati della giunzione
(fig.8). Le cariche fisse, non compensate dalla carica mobile, costituiscono una carica localizzata
nello spazio (carica spaziale), che produce un campo elettrico. Questo campo elettrico esercita una
forza sulle cariche mobili, impedendo l’ulteriore diffusione delle cariche di maggioranza. Al campo
elettrico è associata una differenza di potenziale, che viene detta potenziale di contatto. Si dice che
questa differenza di potenziale costituisce una barriera di potenziale, appunto in quanto si oppone
all’ulteriore diffusione. Il campo elettrico e il potenziale di contatto possono venire calcolati
conoscendo il drogaggio, e quindi la densità della carica fissa.
Viceversa la barriera di potenziale non si oppone al passaggio delle cariche minoritarie, che
p
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
-+
n
-
-
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
+
+
+
+
+
+
-
+
+
+
+
+
+
-
+
ione donatore
-
ione accettore
+
cariche fisse
cariche mobili
xJ
zona di svuotamento
Fig.8: Zona di svuotamento in una giunzione p-n.
circolano liberamente, abbassando la barriera e quindi permettendo un’ulteriore diffusione di
cariche maggioritarie: si ha quindi un equilibrio dinamico tra corrente di diffusione dei portatori
maggioritari e corrente di conduzione, sollecitata dal campo elettrico, dei portatori minoritari.
Questa situazione risulta bene descritta se si ricorre al modello di banda (fig.9). Ponendo a contatto
la parte p e la parte n il livello di Fermi si porta allo stesso livello (in caso contrario si avrebbe un
passaggio di elettroni dalla zona in cui il livello fosse più alto a quella in cui fosse più basso).
Quindi si modificano le bande come mostrato in figura: si vede che gli elettroni della zona n per
poter passare attraverso la giunzione dovrebbero superare una barriera di energia potenziale,
analogamente le lacune dovrebbero scendere una collina di potenziale. Si potrebbe dimostrare che il
potenziale di contatto risulta, nel caso di drogaggi uniformi:
N N
Vo VT ln A 2 D
ni
p
n
EC
EC
EF
EF
EF
EV
EV
zone p, n unite
zone p,n separate
Fig.9: Formazione della barriera di potenziale tra zona p e n.
KT
dove VT
26 mV a temperatura ambiente.
q
4.4.1. Polarizzazione diretta e inversa
Se si chiude il circuito tramite un collegamento esterno tra zona p e zona n, ovviamente non circola
corrente. Se ora si applica alla giunzione una tensione, possono darsi due situazioni, illustrate in
fig.10, dette di polarizzazione diretta e di polarizzazione inversa:
V0
V0
p
p
n
n
+ -
- +
polarizzazione diretta
polarizzazione inversa
Fig.10: Polarizzazione di una giunzione p-n
Nella polarizzazione inversa si alza la barriera, si estende la larghezza della zona di svuotamento.
Le cariche di maggioranza rimangono bloccate, mentre quelle di minoranza passano indisturbate,
dando luogo a una corrente detta di saturazione inversa (saturazione perché passano tutti i portatori
di minoranza disponibili).
Nella polarizzazione diretta la zona di svuotamento si restringe, si abbassa la barriera di potenziale
consentendo il flusso delle cariche di maggioranza.
4.4.2. Correnti nella giunzione p-n. Il diodo
La giunzione p-n costituisce un diodo. Le premesse poste ci consentono di calcolare l’espressione
della corrente della giunzione. Per il principio di continuità la corrente resta costante nelle varie
sezioni della giunzione, tuttavia, a seconda delle sezioni, assume espressioni diverse, potendo essere
prevalentemente di conduzione o di diffusione, dovuta a portatori n o a portatori p.
La fig.11 rappresenta l’andamento delle densità di corrente nella giunzione.
p
n
Jtot
Jpp
Jnn
lacune diffuse
elettroni diffusi
Jpn
Jnp
lp
ln
Fig.11: Densità di corrente in una giunzione p-n
Jnn è una corrente di elettroni in zona n. Analogo il significato degli altri simboli. Il calcolo della
corrente dovuta ai portatori di maggioranza è difficoltoso, perché costituita parte da corrente di
conduzione, parte da corrente di diffusione con una distribuzione fra i due tipi dipendente dalla
sezione che si considera. Osserviamo però che la corrente delle lacune in zona p diventa corrente
esclusivamente di diffusione (portatori di minoranza) quando le lacune passano in zona n, dal
momento che una corrente di conduzione di portatori di minoranza è trascurabile. Considerazioni
analoghe valgono per la corrente di elettroni in zona p. Supponiamo allora, per il calcolo della
corrente, di considerare una sezione posta al limite della zona di svuotamento, nella zona n (si
assume x = ln). La corrente risulta allora data dalla somma di due termini,
J pn x l n e J nn x l n .
Il secondo è di difficile calcolo, ma se la ricombinazione nella zona di svuotamento è trascurabile,
J nn x l n J np x l p .
Si riduce quindi il calcolo della corrente alla somma dei due soli termini di diffusione dei portatori
di minoranza. Ricordando l’espressione della corrente in un semiconduttore, la corrente di
diffusione è data da termini del tipo
n
p
e
.
J n qDn
J p qD p
x
x
E’ sufficiente quindi conoscere le concentrazioni n(x) e p(x) di elettroni e lacune che diffondono e i
loro valori np e pn, ai limiti della zona di svuotamento.
Si può dimostrare, risolvendo l’equazione di diffusione, che queste concentrazioni sono:
V
VT
n p n po ( e
1)
e
V
VT
pn pno ( e
1) ,
dove n po e
pno sono le concentrazioni di equilibrio, V la tensione applicata alla giunzione.
Si vede allora come anche la corrente di diffusione sarà esprimibile con un’espressione che dipende
dall’esponenziale
V
( e VT 1) .
Si trova :
I Is
V
VT
(e
1) .
I s si dice corrente di saturazione inversa e rappresenta praticamente il valore a cui si stabilizza la
corrente per V 0.
L’andamento della corrente è dato dal grafico di fig.12. In esso si distingue una zona di
polarizzazione inversa e una di polarizzazione diretta, in cui la corrente segue un andamento di tipo
esponenziale. In realtà a denominatore dell’esponente è necessario introdurre un termine di
correzione, detto , che varia tra 1 e 2. Per forti tensioni negative si ha la zona di scarica.
Si vede come il diodo sia un elemento dalla caratteristica non lineare, che conduce o non conduce
corrente, a seconda del segno della tensione.
La successiva fig.13 mostra una caratteristica più realistica: il grafico della corrente è ottenuto con
“Matlab”, assumendo per Is il valore di 1 A.
I
polarizzazione diretta
I
VB
-
V
Is
+
V
polarizzazione inversa
Fig.12: Caratteristica corrente tensione e simbolo del diodo. La parte di caratteristica
in polarizzazione inversa è stata disegnata con una scala diversa, per permettere di
apprezzare sul grafico la corrente di saturazione inversa
t=-2:0.01:0.8;
Is=10^(-6);
I=Is*(exp(t./0.05)-1);
plot(t,I);
title(' caratteristica diodo');
xlabel('V - (volt)');
ylabel('ID - (amp.)')
Fig.13:
Caratteristica
corrente tensione di un
diodo calcolata a partire
dall’espressione analitica.
4.4.3. Effetti reattivi della giunzione
Alla giunzione è associato anche un comportamento di tipo capacitivo, dovuto alla variazione
dell’estensione della zona di svuotamento con la tensione applicata e alla corrispondente variazione
di carica fissa nelle zone lasciate scoperte dalla carica mobile. Questo comportamento capacitivo è
rappresentato da una capacità
dQ
, detta capacità di transizione, più sensibile in polarizzazione inversa.
C
dV
In polarizzazione diretta sulla capacità di transizione prevale un altro effetto capacitivo, detto
capacità di diffusione, dovuto alla variazione della carica immagazzinata nelle cosiddette falde di
diffusione, cioè della carica costituita dai portatori di minoranza che diffondono nella zona di
polarità opposta. Si dice che in polarizzazione inversa la capacità della giunzione è prevalentemente
di transizione, in polarizzazione diretta è prevalentemente di diffusione.