Equilibrio per traslazioni
Condizione di equilibrio
In questa sezione vogliamo cominciare a studiare la statica, ossia quella parte della meccanica che si occupa
dell'equilibrio dei corpi. Partiremo con lo studio dell'equilibrio dei corpi per traslazioni. Un corpo subisce una traslazione
quando ogni suo punto si sposta della stessa quantità nella stessa direzione e nello stesso verso, in altre parole quando
ogni suo punto è sottoposto allo stesso vettore spostamento.
In fisica giocano un ruolo importante i cosiddetti corpi rigidi. Un corpo rigido è un corpo che non si può deformare, ossia
un corpo in cui ogni punto mantiene nel tempo la stessa distanza da ogni altro punto del corpo. In generale studiare il
moto o l'equilibrio di un corpo rigido può non essere banale se il corpo rigido non ha forma regolare. Se però il corpo
rigido ha forma regolare (ad esempio sferica) si può immaginare tutta la massa del corpo concentrata in un punto che è il
centro di simmetria del corpo (nell'esempio della sfera, il suo centro). Questo centro di simmetria va anche sotto il nome
di baricentro.
Lo studio del moto oppure dell'equilibrio del corpo rigido viene in questo modo ridotto allo studio del moto oppure
dell'equilibrio di un particolare punto dotato di massa, ossia di un particolare punto materiale. In queste lezioni useremo
sempre per semplicità questo modello del punto materiale, ossia immagineremo tutta la massa M del corpo rigido
concentrata nel baricentro che pertanto risulterà sottoposto a una forza-peso totale pari a M · g, dove g = 9.8 N / kg. Più
in generale, si può utilizzare il modello del punto materiale quando il corpo è molto più piccolo delle dimensioni fisiche
che caratterizzano il problema e quando le direzioni di tutte le forze agenti sul corpo si incontrano in un unico punto.
Anche nel linguaggio di tutti i giorni diciamo che un corpo è in equilibrio quando non si muove. Cerchiamo ora di tradurre
questa definizione a parole di equilibrio in formule matematiche, limitandoci per il momento alle traslazioni. Abbiamo
visto che le forze hanno effetti dinamici, ossia sono in grado di mettere in movimento i corpi ai quali sono applicate. Per
avere equilibrio per traslazioni è perciò necessario che la somma vettoriale di tutte le forze applicate al corpo in esame
sia uguale a 0:
Ad esempio consideriamo due squadre che giocano a tiro alla fune: se una squadra applica una forza diretta
orizzontalmente da destra a sinistra di intensità F e la squadra avversaria applica una forza di ugual intensità F, ma
diretta orizzontalmente da sinistra a destra, avremo che la somma dei due vettori forza, uguali ed opposti, è uguale a
zero e la fune risulta perciò in equilibrio.
Se ragioniamo in termini di componenti dei vettori avremo che, per avere equilibrio, la somma di tutte le componenti
orizzontali dei vettori forza deve essere uguale a zero, così come deve essere uguale a zero la somma di tutte le
componenti verticali dei vettori forza. Vedremo nelle prossime sezioni varie applicazioni di questo concetto.
Forza equilibrante, reazione vincolare
Abbiamo visto nella sezione precedente che la condizione di equilibrio per traslazioni è l'annullamento della forza totale
(detta anche risultante) applicata al corpo. Vediamo quali conseguenze ha questa condizione di equilibrio. Supponiamo
che ci sia una forza che agisce su un corpo. Evidentemente il corpo non è in equilibrio. Come facciamo a ripristinare la
condizione di equilibrio? Possiamo aggiungere una seconda forza uguale ed opposta alla prima, ossia una forza con
ugual direzione, uguale intensità ma verso opposto. Una forza con queste caratteristiche è detta forza equilibrante.
Un esempio in cui entra in gioco la forza equilibrante è quello di un corpo posto su un tavolo. Sappiamo che ogni corpo
dotato di massa è soggetto a una forza-peso. Perché allora il corpo risulta essere in equilibrio? Evidentemente perché
esiste una forza in grado di equilibrare la forza-peso del corpo: il tavolo, con la sua presenza, esercita una forza sul
corpo uguale ed opposta alla forza-peso. Questa particolare forza equilibrante prende il nome di reazione vincolare del
piano:
Ovviamente la forza peso di un corpo può essere equilibrata anche per mezzo di più forze, come nel caso dell'insegna in
figura tenuta in equilibrio grazie alla tensione esercitata da due fili:
1
Usando la regola del parallelogramma è facile verificare graficamente che la somma vettoriale delle due tensioni
esercitate dai fili obliqui è esattamente uguale alla forza-peso dell'insegna. In questo modo la risultante di tutte le forze è
uguale a zero e l'insegna risulta in equilibrio.
Piano inclinato
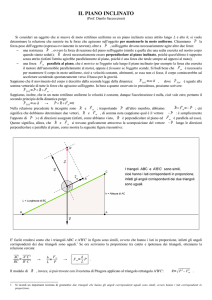
Consideriamo un piano inclinato di altezza AC = h e lunghezza AB = l, come nella seguente figura dove, per semplicità,
un carrello di massa m è rappresentato da un quadrato.
Quando l'attrito è assente, la forza totale che agisce sul carrello è data dalla componente parallela della forza-peso LM
= m · g, dove g = 9.8 N / kg. La componente perpendicolare al piano della forza-peso è infatti compensata dalla reazione
vincolare del piano inclinato. È facile rendersi conto che i triangoli ABC ed LMN sono simili, pertanto hanno i lati in
proporzione, in particolare AB : LM = AC : LN da cui l : mg = h : LN. La componente parallela della forza-peso, che
provoca lo scivolamento del corpo lungo il piano, viene pertanto ad essere uguale a LN = mgh / l.
È interessante considerare due casi limite.
1.
2.
Piano orizzontale: in questo caso l'altezza del piano è uguale a 0, ossia h = 0, da cui la componente parallela
della forza-peso LN = 0. Rimane solo la componente perpendicolare della forza-peso che è interamente
compensata dalla reazione vincolare del piano. Di conseguenza la forza totale applicata al corpo è zero e il
corpo rimane in equilibrio.
Piano verticale: in questo caso h ≈ l e la componente parallela della forza-peso viene a coincidere con la forzapeso mg. Il corpo non risente di alcuna reazione vincolare da parte del piano e cade liberamente.
Un piano inclinato (ad esempio una strada in salita o in discesa) può essere caratterizzato dalla sua pendenza
percentuale, definita come il rapporto tra i due cateti del triangolo ABC, moltiplicato per 100: pendenza percentuale =
AC / BC · 100.
La forza equilibrante nel caso di un piano inclinato sarà una forza diretta lungo il piano inclinato, avente la stessa
intensità della componente parallela della forza-peso LN e verso opposto. Nella prossima sezione allestiremo un
esperimento che ci consentirà di equilibrare con un dinamometro la componente parallela della forza-peso. In questo
modo andremo anche a misurare in maniera indiretta l'intensità della componente parallela della forza-peso.
Esercizi
1.
Quesito: Per tenere in equilibrio un corpo posto su un piano inclinato di altezza h = 40 cm e lunghezza l = 60
cm è necessario applicare una forza pari a 40 N. Si calcoli la massa del corpo posto sul piano inclinato.
Risposta: Siccome la componente perpendicolare della forza-peso è equilibrata dalla reazione vincolare del
piano, rimane attiva la componente parallela della forza-peso. Tale componente è uguale a 40 N. Pertanto
sappiamo che 40 = m · g · h / l da cui possiamo ricavarci il valore della massa posta sul piano: m = 40 · l / (g ·
h) = 40 · 0.6 / (9.8 · 0.4) kg = 6.12 kg.
2
2.
Quesito: Il blocco in figura è in un equilibrio, pur essendo soggetto all'azione di tre forze. Sapendo che F 1 =
7.05 N e F2 = 10 N, si determini il valore dell'intensità della forza F 3.
Risposta: Per risolvere questo esercizio dobbiamo procedere alla scomposizione delle forze 1 e 2. La forza 1 è
inclinata di 45° rispetto all'orizzontale. Pertanto le sue componenti lungo x e y saranno uguali tra loro: F1x = F1y
= 7.05 / 1.41 N = 5 N. Più complicata è invece la scomposizione della forza 2. Siccome l'angolo è di 30°, il
triangolo in figura risulta essere la metà di un triangolo equilatero di lato 10 N. Pertanto la componente verticale
della forza 2 è la metà del lato, mentre quella orizzontale è uguale all'altezza del triangolo equilatero. Il risultato
della scomposizione è F2x = 0.866 · 10 N = 8.66 N mentre F2y = 10 / 2 N = 5 N. Notiamo che F1y = F2y. Dal
momento che queste due componenti sono uguali come intensità ma opposte come verso, il corpo non trasla
lungo l'asse verticale. Affinché il corpo non trasli neanche lungo l'asse orizzontale è necessario che l'intensità di
F3 uguagli la somma delle componenti orizzontali delle altre due forze, ossia F 3 = F1x + F2x = (5 + 8.66) = 13.66
N.
3.
Quesito: Con un dinamometro scopriamo che la componente parallela della forza-peso agente su un corpo
posto su un piano inclinato vale 5 N. Quanto vale la forza-peso del corpo sapendo che il piano inclinato ha
altezza h = 30 cm e lunghezza l = 70 cm?
Risposta: Si tratta ancora una volta di invertire la formula che ci dà la componente parallela della forza-peso
per trovare il peso P = m · g dell'oggetto. Avremo 5 N = P · h / l da cui otteniamo 5 = P · 30 / 70. Si tratta di
un'equazione di primo grado in P che può essere risolta moltiplicando per 70 e dividendo per 30 entrambi i
membri dell'uguaglianza: P = 70 · 5 N / 30 = 11.67 N.
Equilibrio per rotazioni
Momento di una forza
Per introdurre il concetto di momento di una forza partiamo dalla seguente domanda: perché nelle porte le maniglie
sono sempre dalla parte opposta rispetto ai cardini? Supponiamo di voler aprire un vecchio portone poco oliato. Dalla
nostra esperienza sappiamo che si fa meno fatica (in altre parole, è sufficiente applicare una forza minore) spingendo il
portone dalla parte opposta rispetto ai cardini. Altro esempio che ci può aiutare è quello della chiave inglese e del
bullone. Anche in questo caso è molto più facile ruotare il bullone applicando la forza all'estremità del manico della
chiave inglese, ossia nel punto più lontano rispetto al punto attorno al quale avviene la rotazione. Da tutti questi esempi
ricaviamo che, in presenza di un corpo che può ruotare, gli effetti di una forza applicata al corpo dipendono da tre fattori:
1.
2.
3.
l'intensità della forza: se applichiamo una forza maggiore, la rotazione del bullone o del portone risulta essere
agevolata;
il punto di applicazione della forza: a parità di intensità la rotazione è notevolmente agevolata se applichiamo
la forza nel punto più lontano dal centro di rotazione;
la direzione della forza: se applichiamo una forza diretta lungo il manico della chiave inglese non si verifica
alcuna rotazione.
Nella figura riportata sopra O è il punto attorno al quale avviene la rotazione (ad esempio il centro del bullone), b è la
distanza tra la retta d'azione della forza e il punto attorno al quale avviene la rotazione. Questa distanza prende anche il
nome di braccio della forza. Il momento di una forza M si definisce come il prodotto dell'intensità F della forza per la
lunghezza b del braccio: M = F · b. Dal momento che nel Sistema Internazionale la forza si misura in newton e il braccio
in metri l'unità di misura del momento della forza è il newton per metro (N · m). Ad esempio, se l'intensità della forza è F
= 5 N e il braccio misura b = 6 cm avremo un momento della forza pari a M = 5 N · 0.06 m = 0.3 N · m. Come casi
particolari, se la retta d'azione della forza passa per il centro di rotazione O abbiamo che b = 0. In questo caso il
momento della forza si annulla e non si verifica alcuna rotazione.
Il momento di una forza è la grandezza che regola i movimenti di rotazione. A questo punto è chiaro che possiamo
aumentare il momento M sia aumentando l'intensità della forza F sia aumentando il braccio b: questo è il motivo per cui il
3
portone si apre più facilmente se lo spingiamo dalla parte opposta rispetto ai cardini o per cui il bullone si allenta più
facilmente spingendo una chiave inglese all'estremità del manico. Per convenzione si associa un segno alle rotazioni: il
momento di una forza è un numero positivo se le rotazioni che esso provoca sono antiorarie, è invece un numero
negativo se le rotazioni che esso induce sono orarie. Questa convenzione sarà di fondamentale importanza nella
prossima sezione, dove andremo a stabilire quali sono le condizioni di equilibrio di un corpo che può ruotare.
Condizione di equilibrio
Abbiamo visto che, nel caso dei moti di traslazione, la condizione di equilibrio è data dall'annullarsi della risultante delle
forze applicate al corpo. Vogliamo ora chiarire qual è la condizione di equilibrio per un corpo che è libero di ruotare.
Abbiamo visto nella precedente sezione che il momento di una forza assume segni positivi o negativi a seconda del
senso in cui avviene la rotazione. La condizione di equilibrio per rotazioni è data dall'annullarsi della somma di tutti i
momenti che vengono applicati al corpo, ossia: Mtot = M1 + M2 + M3 + ... = 0. Se prescindiamo dai segni, possiamo anche
dire che un corpo non ruota quando la somma di tutti i momenti orari applicati al corpo è uguale alla somma di tutti i
momenti antiorari. Questa è la condizione di equilibrio per rotazioni.
Come esempio di equilibrio per rotazioni consideriamo una bilancia a bracci diseguali, come nella seguente figura:
Il peso P1 induce una rotazione antioraria di momento M1 = P1 · b1, il peso P2 induce invece una rotazione oraria di
momento M2 = - P2 · b2. La bilancia sarà in equilibrio non quando i due pesi sono uguali ma quando si annulla il
momento totale: Mtot = M1 + M2 = 0, ossia quando il momento antiorario P1 · b1 è uguale al momento orario P2 · b2.
Quesito: Si consideri l'asta in figura: la stessa forza-peso di intensità P = 30 N viene applicata in due punti posti
rispettivamente a b1 = 40 cm a sinistra e a b2 = 20 cm a destra del punto attorno al quale l'asta può ruotare. Si stabilisca
dove deve essere posto un ulteriore peso di intensità P3 = 15 N per fare in modo che l'asta rimanga in equilibrio.
Risposta: Tenendo conto che a rotazioni orarie (antiorarie) corrispondono momenti negativi (positivi) avremo che il
momento antiorario è M1 = P · b1 = 30 N · 0.40 m = 12 N · m. Il momento orario è invece dato da M 2 = - P · b2 = - 30 N ·
0.20 m = - 6 N · m. Il momento totale diventa: M = (12 - 6) N · m = 6 N · m. Questo vuol dire che, se non aggiungiamo
contrappesi, l'asta tende a ruotare in senso antiorario. Pertanto il peso di P = 15 N dovrà essere posto alla destra del
punto di rotazione in modo tale da produrre un momento orario M = - 6 N · m. Se indichiamo con b la distanza cercata,
dovremo risolvere la seguente equazione di 1° grado: - 6 N · m = - (15 N) · b da cui b = 6 / 15 m = 0.4 m = 40 cm.
Applicazioni
Coppia di forze. Supponete di voler mettere in rotazione la gomma posta sul vostro banco senza nel contempo farla
traslare. Una possibilità è quella di applicare alle due estremità della gomma due forze aventi la stessa direzione, la
stessa intensità e verso opposto, come nella figura sottostante. Due forze con queste caratteristiche prendono il nome di
coppia di forze.
4
Il fatto che le due forze abbiano uguale intensità garantisce che non ci sia alcun moto di traslazione. Viceversa le due
forze generano entrambe una rotazione in senso antiorario. Per esercizio potete provare che il momento totale della
coppia è dato da M = F · l dove F è l'intensità delle due forze mentre l è la lunghezza della gomma. Due coppie di forze
si dicono equivalenti quando hanno lo stesso momento.
Molte macchine di uso comune si basano sui principi fisici che abbiamo descritto nelle ultime sezioni. Due esempi sono
costituiti dalla carrucola e dal verricello illustrati nella seguente figura:
Partiamo dall'analisi della figura di sinistra: una carrucola. In questo caso le forze in gioco sono due: la forza motrice Fm
che tende a generare una rotazione antioraria di momento Fm · 2r e la forza-peso Fp che tende a generare una rotazione
oraria di momento - Fp · r. Se vogliamo sollevare il peso, il momento della forza motrice deve avere intensità maggiore
del momento dovuto alla forza-peso, ossia: Fm · 2r > Fp · r. Dividendo la precedente relazione per r otteniamo che F m >
Fp / 2, in altre parole è sufficiente applicare una forza motrice pari alla metà della forza-peso per riuscire a sollevare il
carico.
Un discorso analogo vale nel caso del verricello, riportato nella figura di destra. Il centro di rotazione in questo caso
coincide con l'asse del cilindro. La forza-peso genera una rotazione antioraria di momento F p · r, dove r è il raggio del
cilindro. La forza motrice invece genera una rotazione in senso orario di momento - Fm · l, dove l è la lunghezza dell'asta
del verricello. Per sollevare il carico, il momento della forza motrice deve avere un'intensità maggiore di quello della
forza-peso, ossia Fm · l > Fp · r da cui Fm > Fp · r / l. Per minimizzare la fatica (ossia la forza motrice da applicare)
andremo a costruire verricelli con piccoli valori del raggio r e grandi valori della lunghezza dell'asta l. Ad esempio se r =
10 cm e l = 100 cm, sarà sufficiente una forza motrice pari a 1/10 della forza peso per sollevare il carico.
Per concludere questa sezione, vogliamo ricordare come un esempio di verricello presente nella nostra vita di tutti i
giorni è costituito dai pedali e dalla ruota dentata della nostra bicicletta: i pedali giocano il ruolo della manovella del
verricello, mentre la ruota dentata gioca il ruolo del cilindro del verricello. Per ridurre la fatica e rendere più leggera l a
pedalata è necessario ridurre il raggio r della ruota dentata.
Baricentro ed equilibrio
Esistono tre possibili posizioni di equilibrio di un corpo: equilibrio stabile, equilibrio instabile ed equilibrio indifferente.
Vogliamo illustrarle partendo dall'esempio in figura:
La sfera A occupa una posizione di equilibrio stabile: se spostiamo la sfera dalla posizione di equilibrio, lei tende a
tornare nella posizione di partenza. La sfera B occupa invece una posizione di equilibrio instabile: se la allontaniamo
dalla posizione di equilibrio, la sfera si allontana sempre più dalla posizione di partenza. La sfera C invece occupa una
posizione di equilibrio indifferente: se la allontaniamo dalla posizione di partenza lei si sposta per assumere una nuova
posizione di equilibrio. Su un piano orizzontale ogni punto corrisponde a una posizione di equilibrio.
5
In alcune situazioni la posizione del baricentro (ossia il punto in cui possiamo pensare concentrata tutta la massa di un
corpo) gioca un ruolo importante nella classificazione delle posizioni di equilibrio. Supponiamo di avere un'asta
omogenea. La possiamo appendere ad un punto posto sopra il baricentro, ad un punto posto sotto il baricentro o ad un
punto coincidente con il baricentro, come nella figura sottostante:
Nella figura di sinistra il baricentro sta al di sotto del punto di rotazione. La posizione verticale dell'asta è una posizione di
equilibrio stabile: infatti se spostiamo l'asta dalla posizione verticale si genera un momento orario che tende a riportare
l'asta nella sua posizione di partenza. Nella figura centrale invece il baricentro sta al di sopra del punto di rotazione.
L'equilibrio è instabile: infatti se spostiamo l'asta dalla posizione di equilibrio il momento orario tende ad allontanare
l'asta dalla posizione di partenza e a rovesciarla. Nella figura a destra invece il baricentro coincide con il punto attorno al
quale avviene la rotazione. In questo caso l'equilibrio è indifferente e l'asta tende a rimanere nella nuova posizione in
cui è stata portata. Infatti, poiché la retta d'azione della forza-peso passa per il centro di rotazione, abbiamo che il
momento della forza-peso è nullo e non si genera alcuna rotazione.
Nella valutazione dell'equilibrio di un corpo assume la sua importanza anche la posizione relativa del baricentro e della
superficie d'appoggio. Per avere equilibrio è fondamentale che la verticale passante per il baricentro di un corpo cada
all'interno della superficie d'appoggio del corpo stesso. Se invece tale verticale interseca il perimetro della superficie
d'appoggio allora l'equilibrio diventa instabile. Se infine la verticale per il baricentro cade fuori dalla superficie d'appoggio
del corpo in esame allora la situazione non è più di equilibrio perchè si genera un momento in grado di far ruotare il
corpo.
6