Formule

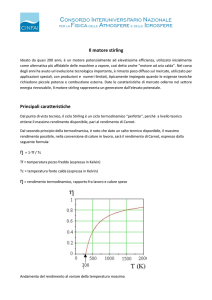
Formule
A volte si vuole costruiore uno stirling senza partire da un progetto già esistente.
In questi casi è importante avere a disposizione un formulario in grado di indicare le proporzioni e le forze che
agiscono nel motore.
Ecco una pagina che contiente le formule necessarie per capire e progettare Stirling di tipo alfa, beta e gamma.
Per comprenderla è fondamentale avere conoscenze matematiche.
Attenzione! Il testo qui riprodotto è stato tradotto automaticamente, potrebbe contenere errori.
1. INTRODUZIONE
La teoria Schmidt è uno dei metodi di calcolo per la isoterma di Stirling motori. E 'il metodo più semplice e
molto
utile
durante
lo
sviluppo
del
motore
di
Stirling.
Questa teoria si basa sul isoterma di compressione e di espansione di un gas ideale.
2. ASSUNZIONE DI SCHMIDT TEORIA
Le prestazioni del motore può essere calcolato un diagramma PV. Il volume nel motore è facilmente calcolato
utilizzando la geometria interna. Quando il volume, la massa del gas di lavoro e la temperatura è deciso, la
pressione è calcolato utilizzando un metodo ideale di gas, come indicato nella equazione (1).
(1)
Il
motore
può
essere
calcolata
in
applicazione
dei
seguenti
presupposti:
(a) Non vi è alcuna perdita di pressione in scambiatori di calore e non ci sono differenze di pressione interna.
(b)
(c)
Il
processo
Condizioni
(d)
di
di
espansione
lavoro
Non
vi
e
il
del
processo
gas
è
è
di
compressione
cambiato
una
isotermo
come
un
modifiche.
gas
perfetta
ideale.
rigenerazione.
(e) L'espansione dello spazio morto mantiene la temperatura del gas di espansione - TE, la compressione dello
spazio
morto
mantiene
la
temperatura
del
gas
di
compressione
-
TC
durante
il
ciclo.
(f) La temperatura del gas rigeneratore è una media della temperatura del gas di espansione - TE e la
compressione
di
gas
temperatura
(g) L'espansione dello spazio - VE e la compressione spazio - VC cambia in base sine curve.
La tabella 1 mostra i simboli utilizzati Schmidt Teoria.
Tabella 1 Simboli
-
TC.
3. ALPHA-TIPO MOTORE DI STIRLING
La Figura 1 mostra il modello di calcolo di tipo alfa-motore di Stirling.
2
Fig.
Alpha-1
tipo
di
motore
di
Stirling
I volumi di espansione e compressione cilindro in un determinato angolo di manovella sono determinati in un
primo momento. Il momental volumi è descritta con un angolo di manovella - x. Questo angolo di manovella è
definito come x = 0, quando l'espansione del pistone si trova la posizione più in alto (punto morto superiore).
L'espansione del volume momental - VE è descritto in equazione (2) con una cilindrata di espansione del pistone
- VSE, un volume morto di espansione - VDE, a condizione di assunzione (g).
(2)
La compressione del volume momental - VC si trova in equazione (3) con una cilindrata di compressione a
pistoni - VSC, un volume morto di compressione - VDC e di un angolo di fase - dx.
(3)
Il volume totale momental è calcolato in equazione (4).
(4)
Con le ipotesi (a), (b) e (c), la massa totale del motore - m è calcolata utilizzando il motore di pressione - P,
ogni temperatura - T, ogni volume - V e il gas costante - R.
(5)
La temperatura rapporto - t, una cilindrata rapporto - v volume morto e di altri rapporti sono trovato con le
seguenti equazioni.
(6)
(7)
(8)
(9)
3
(10)
La temperatura rigeneratore - TR è calcolato in equazione (11), mediante l'assunzione (f).
(11)
Quando l'equazione (5) è stato modificato utilizzando la formula (6) - (10), la massa totale del gas - m è
descritto nel prossimo equazione.
(12)
Equazione (12) è cambiato in equazione (13), utilizzando la formula (2) e (3).
(13)
Ora;
(14)
(15)
(16)
Il motore di pressione - P è definita come una prossima equazione, utilizzando l'equazione (13).
(17)
La media della pressione - Pmean può essere calcolato come segue:
(18)
c è definito nei prossimi equazione.
(19)
4
Come risultato, il motore di pressione - P, in base alla media pressione motore - Pmean è calcolato in equazione
(20).
(20)
D'altro canto, in caso di equazione (17), quando cos (xa) =- 1, il motore di pressione - P è la pressione minima Pmin, la prossima equazione è introdotto.
(21)
Pertanto, il motore di pressione - P, in base alla pressione minima - Pmin è descritto in equazione (22).
(22)
Allo stesso modo, quando cos (xa) = 1, il motore di pressione - P è la pressione massima - Pmax. La seguente
equazione è introdotto.
(23)
Il diagramma PV di Alpha-tipo di motore di Stirling può essere fatta con le equazioni di cui sopra.
4. BETA-TIPO MOTORE DI STIRLING
Allo stesso modo, le equazioni di tipo beta-motore Stirling sono dichiarate. La Figura 2 mostra un modello di
calcolo di un beta-tipo di motore di Stirling.
Fig. Beta-2 tipo di motore di Stirling
L'espansione del volume momental - VE e la compressione momental volume - VC sono descritte nei seguenti
equazioni, con una cilindrata di un pistone displacer - VSE, una cilindrata di potenza pistone - VSC e un angolo
di fase-dx tra il displacer pistone e la potenza del pistone.
5
(24)
(25)
Nel caso del beta-tipo di Stirling motore, il pistone e displacer la potenza del pistone si trovano nello stesso
cilindro. Quando entrambi i pistoni si sovrappone ictus, un effettivo spazio di lavoro è stato creato. La
sovrapposizione di volume - VB in equazione (25) può essere calcolato nei prossimi equazione.
(26)
Poi il volume totale momental - V si trova nella equazione (27).
(27)
Il motore di pressione - P basa la media pressione - Pmean, la pressione minima - Pmin e la pressione massima Pmax sono descritte nei seguenti equazioni come l'alfa-tipo di motore di Stirling.
(28)
Diversi rapporti e coefficienti sono definiti come segue.
(29)
(30)
(31)
(32)
(33)
6
(34)
(35)
(36)
(37)
(38)
Il fotovoltaico schema di Beta-tipo di motore di Stirling può essere fatta con le equazioni di cui sopra.
5.
GAMMA-TIPO
MOTORE
DI
STIRLING
La figura 3 mostra un modello di calcolo di un gamma-tipo di motore di Stirling.
Fig. 3 Gamma-tipo di motore di Stirling
Analoghe le equazioni di calcolo sono fatti come l'alfa e beta-tipo di motore. L'espansione del volume momental
- VE e la compressione momental volume - VC sono descritte nei seguenti equazioni con una cilindrata di un
pistone displacer - VSE, una cilindrata di potenza pistone - VSC e un angolo di fase - dx tra il pistone e displacer
la potenza del pistone.
(39)
(40)
Il volume totale momental - V è descritta una prossima equazione.
7
(41)
Il motore di pressione - P basa la media pressione - Pmean, la pressione minima - Pmin e la pressione massima Pmax si trovano nelle seguenti equazioni.
(42)?
Adesso,
(43)
(44)
(45)
(46)
(47)
(48)
(49)
(50)
(51)
Il fotovoltaico schema-tipo di Gamma Stirling motore può essere fatto con le equazioni di cui sopra.
6. INDICATO ENERGIA, POTENZA ED EFFICIENZA
8
I energia (area del diagramma PV) per l'espansione e la compressione dello spazio può essere calcolato come
uno soluzioni analitiche con l'uso dei suddetti coefficienti. I energia in espansione dello spazio (indicato
espansione di energia) - WE (J), sulla base della media pressione - Pmean, la pressione minima - Pmin e la
pressione massima - Pmax sono descritte nei seguenti equazioni.
(52)
L'energia indicato nella compressione dello spazio (indicato compressione energia) - WC (J) sono descritte nella
prossima equazioni.
(53)
I energia per un ciclo di questo motore - Wi-(J), è richiesto nei prossimi equazioni.
(54)
Le relazioni tra Pmean, Pmin Pmax e sono determinati nei seguenti equazioni.
(55)
(56)
La potenza indicata espansione - LE (W), il potere di compressione - LC (W) e la potenza indicata di questo
motore - Li (W), sono definiti nei seguenti equazioni, utilizzando il motore per un secondo, n (RPS, Hz).
(57)
(58)
(59)
L'espansione di energia - abbiamo trovato l'equazione (52), un ingresso di calore da una sorgente di calore per il
motore. La compressione di energia - Wc calcolato equazione (53) si intende un respingere il calore del motore
di raffreddamento ad acqua o aria. Poi il rendimento termico del motore - e si calcola nel prossimo equazione.
(60)
Questa efficienza è pari a quella di un ciclo di Cornot che è la più massima efficienza in ogni motore termico.
9
questa pagina è tratta da questo sito
10