Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
A.A. 2005
Appunti su data base
di:
Anna Maria Carminelli Gregori
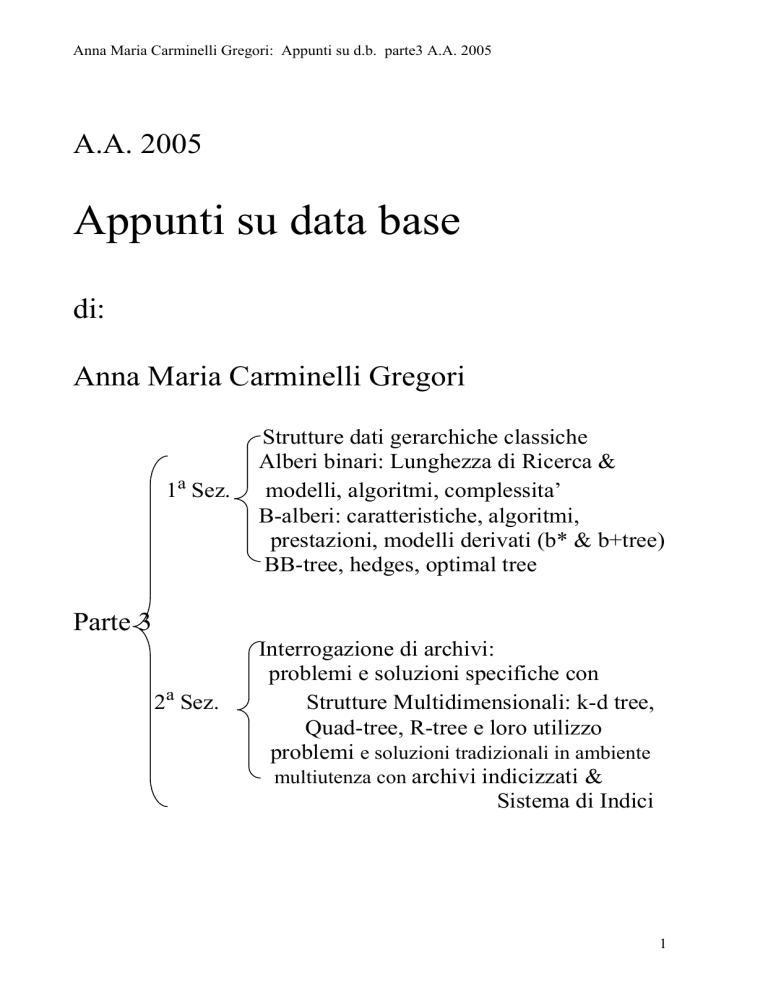
1a Sez.
Strutture dati gerarchiche classiche
Alberi binari: Lunghezza di Ricerca &
modelli, algoritmi, complessita’
B-alberi: caratteristiche, algoritmi,
prestazioni, modelli derivati (b* & b+tree)
BB-tree, hedges, optimal tree
Parte 3
2a Sez.
Interrogazione di archivi:
problemi e soluzioni specifiche con
Strutture Multidimensionali: k-d tree,
Quad-tree, R-tree e loro utilizzo
problemi e soluzioni tradizionali in ambiente
multiutenza con archivi indicizzati &
Sistema di Indici
1
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Nella Parte 2 si e’ visto come le varie componenti dei
DBMS, qualunque sia il loro modello, utilizzino al
loro interno alberi e strutture gerarchiche.
Come introduzione e aggancio con le parti precedenti,
si ricordi che nell’ ambito della progettazione fisica
del d.b. la scelta dei parametri che il DBMS richiede
all’ utente riguarda anche le strutture fisiche usate e
le
loro
caratteristiche
come
dimensioni,
configurazione, modalita’ d’ uso. Ogni DBMS ha
pochi ma importanti tipi di strutture per memorizzare i
dati ed accedervi, per esempio tramite indici.
Nei DBMS l’ accesso ai dati si puo’ riassumere nel
modo seguente:
il gestore dei metodi di accesso usa le richieste
prodotte dall’ ottimizzatore per scegliere e attivare il
metodo di accesso disponibile che il buffer manager
trasforma nelle primitive di accesso ai blocchi
componenti le strutture dati.
Le strutture dati piu’ usate negli RDBMS sono
quelle di tipo gerarchico che saranno trattate in
questa ultima parte.
L’ uso di alberi binari e’ gia’ stato mostrato nel
problema del Sort (parte 1) e solo accennato in parte 2
parlando dell’ ottimizzatore che, per scegliere una sua
strategia, usa strutture dati come alberi binari di
decisione o alberi a +rami per le alternative, come
descritto in Atzeni &… 1999, cap.9.
2
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Un albero binario di decisione detto anche di
confronto o di ricerca si puo’ ottenere dall’ algoritmo
di ricerca binaria estraendo l’ azione dell’ algoritmo e
rappresentando ogni confronto con un nodo dell’
albero. … ma prima di usare la terminologia tipica
occorre definire tutto !
GRAFI, ALBERI, definizioni classica e ricorsiva,
terminologia, caratteristiche …
Grafo: … rappresentazione di una Relazione Binaria tra
elementi di insiemi come in ES.1 di Grafo “bipartito”
ES.1
nodi
a1
a2
archi
b1
b2
Rappresentazione diagrammatica della relazione “ai e’
costruito da bj” o “bj costruisce ai” mentre la relazione
omogenea
“a
i e’ cuoco di aj” e’ rappresentata con un
grafo orientato dove in uno stesso insieme i nodi sono
tra loro (auto)-collegati (da archi con frecce) anche in
maniera
ciclica.
Implementazione? Strutture dati Statiche (matrice
delle adiacenze) e/o Dinamiche come Alberi.
3
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
ALBERO: definizione classica grafo connesso
privo di circuiti chiusi;
struttura vuota;
definizione ricorsiva
un nodo concatenato con M
alberi disgiunti (sottoalberi)
Rappresentazione di
un albero di 10 nodi e 9 rami
F
D
liv. 1 (radice)
A
D
B F
E
liv. 2 (figli)
B
E
A C
H I G
liv. 3
C
H
L
liv. 4
I
G Altra Rappresentazione di alberi:
L
Insiemi Nidificati
Definizioni di:
Grado di un nodo # sotto-alberi del nodo;
“ dell’ Albero = d max. grado dei suoi nodi;
Lunghezza lx di un nodo X # nodi da
attraversare (confrontare con X) per trovarlo
entrando dalla radice e … senza tornare indietro:
lx é pari al livello del nodo se la radice e’ a liv.1
o al livello +1 se la radice e’ a liv.0
4
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Albero orientato caso generale; Albero ordinato
significativo l’ ordine di disposizione dei nodi, per es.
B
B
A
C
C
A
Ordinati sono gli alberi binari di ricerca (def. tra 2
luc.)
Lunghezza interna Li di un albero di n nodi
somma delle lunghezze dei singoli nodi
n
h
Li = li = i ni
i=1
dove risulta:
i=1
ni = # nodi a livello i;
h = altezza dell’ albero con radice a livello 1 e quindi
(considerando fisso il grado)
Li = f(h) con f da determinare.
Lunghezza interna media di un albero di n nodi
P i = Li /n
Significato numero medio di confronti per trovare
un nodo presente nell’ albero entrando dalla radice.
Li e P i si contrappongono a Le = lunghezza esterna: P e
= lunghezza esterna media dell’ albero di n nodi:
modello Albero esteso in cui nodo ha grado =
grado d dell’ Albero se il nodo X ha n figli con n
< d si aggiungono figli fittizi (nodi esterni) e rami a
tali figli.
Esempio di Albero binario esteso:
si tratta di un Albero di ricerca Esteso col significato
seguente:
5
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
In un Albero normale si memorizza un
5
campione C ed i nodi normali
sono gli elementi di C, mentre
7
l’ Universo restante U-C non
1
e’ rappresentato;
i nodi esterni dell’ Albero
…
3
key <1
.
Esteso sintetizzano U-C;
1< key <3
3<key<5
N.o nodi esterni m
n*d+1=n+m
9
…
.
9 < key
… perche’ ? Si uguaglia il N.o dei rami (compreso
quello alla radice) calcolato in 2 modi:
a sinistra del simbolo = col grado dell’ Albero
a destra col N.o totale dei nodi.
Se d=2 m = n+1
Si noti:
il modello Albero Esteso si puo’ “applicare” ad Alberi
di qualsiasi grado d;
si arriva ad un nodo esterno con un numero di
confronti pari al livello del nodo esterno –1… Ricerca
senza successo ! cfr. +oltre.
ALBERO BINARIO: albero di grado 2;
struttura dati ricorsiva;
# nodi a livello 1: 21 nodi al piu’; (Radice);
a livello 2: 21 nodi al piu’;
a livello 3: 4=22 nodi al piu’;
a livello 4: 8=23 nodi al piu’;
6
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
# nodi a livello h: 2h-1 nodi al piu’…
MAX. N.o nodi ammessi in un Albero Binario di
altezza h e’:
N2(h) = 1+2 + 2 2 + 2 3 + … + 2 h-1 = 2 h –1
Quindi risulta:
N2(h) +1 = 2h
log2 (N2(h) +1) = h.
L’ Albero Binario di N2(h) nodi si dice completo sino
all’ ultimo livello MAX. Densita’ delle
informazioni.
ALBERO BINARIO di ricerca = albero binario
ordinato dove dato l’ albero:
nodo
/
\
sotto_alb.
sotto_alb.
sinistro
destro
risulta:
key(sotto_alb. sinistro)< key(nodo)< key(sotto_alb. destro)
Lunghezza interna media di un ALBERO e’ definita
come:
h
Pi
= Li /n = 1/n i n i = 1/n f(h)
i=1
fornisce una misura della
lunghezza media di ricerca di un nodo definita come il
numero medio di confronti per trovare un nodo
presente nell’ albero entrando dalla radice.
e
7
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Ricerca con successo in un ALBERO BINARIO
N.o di confronti medio Cmedio per la ricerca di un nodo
di data chiave presente in un albero binario di n nodi
ed altezza h:
_ se il livello della radice e’ 1 ed il nodo e’ a livello i
Ci = i ;
_ se il livello della radice e’ 1 e a livello i ci sono ni
nodi Cni = i ni
n
h
i=1
i=1
N. totale di confronti Ctot = Li = (Ci) = (Cni)
o
N.o di confronti medio Cmedio = Li /n =
Altra espressione: Cmedio =
Pi
=
n
Pi
(h’(i)/n)
(*)
i=1
dove: h’(i) = lunghezza nodo i = livellonodo i se livello radice = 1
h’(i) = lunghezza nodo i = livellonodo i +1 se livello radice = 0.
L’ espressione (*) appare come la somma delle
lunghezze dei nodi pesate con le probabilita’ di
accesso ai nodi in condizioni di equiprobabilita’;
se i nodi NON sono equiprobabili allora si ha:
n
Cmedio =
Pi
= (h’(i) pi) con
i=1
n
(pi) =1
i=1
espressione che si ritroverà negli alberi ottimi.
8
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
In un ALBERO BINARIO anche incompleto sull’
ultimo livello per il quale quindi risulti:
h-1
h
2 n < 2 -1
si ha:
Cmedio = O(log2 n)
Si dimostrera’ quindi che in condizioni di
equiprobabilità:
P i = O (h) = O (log2 (n))
sia per alberi binari completi fino a livello h (altezza
dell’ albero),
sia per alberi binari completi fino a livello h-1, ma
incompleti a livello h.
Ricerca senza successo in un
ALBERO BINARIO:
per P e espressioni analoghe definite su alberi estesi. In effetti: la
Ricerca senza successo in un ALBERO BINARIO
termina in un nodo esterno !
C’medio= N.o di confronti medio in ricerca senza successo.
Se il nodo esterno e’ a livello i risulta: C’i = i -1;
C’ =
h+1
i=1
n’i C’i =
h+1
n’i (i –1) =
i=1
h+1
i=1
n’i i -
h+1
n i’=
i=1
= Le– m
essendo m il N.o totale dei nodi esterni ed n’i il N.o dei nodi esterni
a livello i.
C’medio= C’/m = Le/m – 1 =
Pe–
1
9
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Cmedio e C’medio sono linearmente dipendenti
noto uno …
Cmedio= (1 +1/n) C’medio –1
Dimostrazione ?! …
Conclusione:
se P e = minima anche P i = minima e naturalmente
anche se Le = minima anche Li= minima albero
bilanciato !
Per convincersene basta considerare un Albero Binario di
altezza h=3 e con # nodi normali N= 7 ed esterni m=8
se l’Albero Binario e’ completo fin l’ultimo livello i
nodi esterni sono tutti a livello 4 e quindi Le= 8*4 = 32.
Qualsiasi altra forma dell’ Albero Bin. (da quello
incompleto sugli ultimi 3 livelli alla lista lineare) hanno Le
maggiore
la lista lineare ha Le= 8*2+7+6+5+4+3+2 = 43;
quello incompleto sugli ultimi 3 livelli ha
Le=5*2+4*5+3*1=33
come appare dall’ esempio che
segue.
10
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Lunghezza interna media di un ALBERO di n nodi:
P i=
Li /n = 1/n
h
i n i = 1/n f(h)
i=1
In un albero binario completo di altezza h ossia
con n = 2 h –1
Li = 1 + 2*2 + 4*3 + 8*4 +…+ 2
h-1
*h =
h
2
i-1
*i
i=1
Si dimostra che:
P i= Li /n = O(h) = O(log2 n)
La dimostrazione si basa su un’ espressione di Li piu’
compatta che e’:
Li = 1 + 2 h (h-1)
P i= Li /n = Li /(2 h –1) = O(h) = O(log2 n)
e quest’ ultima espressione vale anche se l’ ultimo livello
dell’ A.B. non e’ completo.
La dimostrazione procede da A.B. completo partendo da:
Li = 1 + 2*2 + 4*3 + 8*4 +…+ 2
h-1
*h =
h
2
i-1
*i
i=1
e ponendo per prima cosa:
Li - 1 = 2*2 + 4*3 + 8*4 +…+ 2 h-1 *h =
= 2*2 + 2 2 *3 + 2 3 *4 +…+ 2 h-1 *h
=
h
2
i-1
=
livelli
*i
i=2
11
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Si ricorda la progressione geometrica di ragione 2*x data
da (Esp.1):
S(x) = 1 + 2*x + (2 *x) 2 + (2 *x) 3 +…+ (2 *x) h-1
(S(x) – 1) = 2*x + (2 *x) + (2 *x) +…+ (2 *x)
2
3
h-1
h-1
= (2 x)
e moltiplicando per x si ha
i=1
(S(x) – 1) *x = 2*x + 2 *x + 2 *x +…+ 2
2
2
3
i
3
4
h-1
h-1 i
*x = 2 x
h
i+1
i=1
La derivata rispetto a x della precedente espressione e’:
/x ((S(x) – 1) *x)=2*2*x + 3*22 *x2 +4*23 *x 3 +…+ h*2 h-1 *x h-1
h-1
= (i+1)*2 x
Posto x=1 risulta:
i
i
i=1
h-1
[/x ((S(x) – 1) *x)]x=1 = (i+1)*2 =
i
h
2
i-1
*i
[S’x *x + (S(x) – 1)]x=1= Li – 1 Li=1+la derivata x=1!
i=1
i=2
Ricordando la somma della prog. Geometrica Esp.1
S(x) = ((2 *x) h – 1) / (2*x– 1)
e calcolatane la derivata per x=1(*) si ottiene
Li = 1 + 2 h (h –1) e (asintoticamente come indicato di seguito)
= Li/n = Li /(2 h –1) = O(h) = O(log2 n)
________________________________________________
Pi
(*) S’x = ( (2h *h*xh-1)*(2*x – 1) – 2*((2 *x)h – 1) ) / (2*x– 1) 2
[S’x]x=1 = 2h* h – 2*(2h– 1)
[S’x *x + (S(x) – 1)]x=1=2h *h– 2*(2h– 1) + 2h – 1 – 1= 2h*(h– 1)
12
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ ultima espressione di Li per A.B. completo fino al livello
h, che e’:
Li = 1 + 2 h (h –1) si puo’ porre anche in funzione del
numero di nodi n= 2 h –1 (o: n+1 = 2 h): si ottiene
Pi
= Li/n = (1 + 2 h (h –1))/n= (1 + (n+1)(h –1))/n=
=((n+1)*h – n)/n = (1+1/n)*h – 1
Pi
e quindi
= (1+1/n)* log2( n+1) –1
lim
n
Pi
= log2( n) ossia
= O(log2 n).
Pi
Per ottenere l’ espressione analoga per A.B. incompleto a
livello h, ma completo fino a livello h-1 si considerano
alcune disuguaglianze. In questo caso: n+1 2 h e quindi:
2 h-1 n 2 h –1
h–1 log2n
log2( n+1) < h
e quindi anche:
h–1 log2n < h
h 1+ log2n
Definita Linc la lunghezza di ricerca per A.B. incompleto di
n nodi si ha:
Linc = Li – h*nh dove: nh = # nodi mancanti a livello h e
nh < 2 h-1 altrimenti il liv. h sarebbe
e anzi risulta:
nh = (2 h –1) – n
essendo 2 h –1 il numero di nodi dell’ A.B.completo.
13
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Si capisce subito che nh è trascurabile quando n ,
comunque si può dimostrare nel modo seguente:
Linc = Li – h*(2 h –1 – n) =1 + 2h (h –1) –h*2h + h + h*n
Linc = 1– 2 h + h*(1+n)
Da questa espressione ricordando che:
n (2 h –1) ossia (n + 1) 2 h o anche: –(n + 1) > –2 h
segue:
L inc = 1– 2 h + h*(1+n) 1 –(n + 1) + h*(1+n)
Linc 1 + (1+n)*(h-1)
P inc
= Linc/n
lim
P inc
n
lim ( 1/ n + ((1+n)*(h-1))/n )=lim (h*(1+n)/n –1)=
n
n
= O(log2n) avendo sostituito h con 1+ log2n,
dato che: h 1+ log2n
In conclusione si e’ giunti al risultato che:
P i = O (h) = O (log2 (n))
per alberi binari completi e incompleti sull’ultimo livello e
quindi
Cmedio = O(log2 n)
partendo dall’ ipotesi della completezza dell’ A.B. e poi
estendendola ad A.B. con l’ultimo livello incompleto ...
14
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Bisogna quindi vincolare gli A.B. ad essere
il piu’ possibile completi.
1) ALBERO BINARIO Perfettamante
BILANCIATO:
per ogni nodo vale: n(ss) = n(sd) +1
(n = N.o di nodi)
2) ALBERO BINARIO BILANCIATO secondo il criterio AVL
(Adelson-Velskii & Landis)
per ogni nodo vale: h(ss) = h(sd) +1
(h = altezza dell’ albero che puo’ essere incompleto sugli ultimi
livelli come accade per gli alberi di Fibonacci cfr. piu’ oltre)
ALBERO BINARIO E RIPRISTINO
BILANCIAMENTO:
pesante per il perfetto bilanciamento 1): dipende da n,
semplice per il bilanciamento tipo AVL 2): dipende da h.
Costruzione di un ALBERO BINARIO perfettamante
BILANCIATO: function tree (n) cfr. Wirth pag. 196
Costruzione di un ALBERO BINARIO AVL BILANCIATO:
procedure search (x, VAR p, VAR h) cfr. Wirth pag. 220-221 e
+oltre;
PERCHE’ il BILANCIAMENTO ? Occorre PREMUNIRSI
contro la degenerazione in lista lineare ove P = O(n) e
tendere a P = O(log2n)
15
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
REALIZZAZIONE:
IN GENERALE la Costruzione di una struttura DINAMICA implica la
definizione completa di ogni nodo con le operazioni di:
_ prelevare dalla memoria libera 1 nodo;
_ definirne tutti i campi;
_ concatenarlo tramite la definizione del puntatore di
collegamento generalmente passato per indirizzo.
ALBERO BINARIO DI RICERCA: tipica struttura dinamica
USO: efficienti operazioni di ricerca, Ordinamento …
Chiave(albero sin.) < Chiave (nodo) < Chiave(albero ds.)
d
/
\
b
/
a
f
\
/
c e
\
g
puntatori vuoti
a<b<c<d<e<f<g
REALIZZAZIONE ALBERO BINARIO DI RICERCA:
concatenazione espressa a mezzo di due puntatori: left, right
Chiave, informaz.
left
right
Nell’ implementazione che viene descritta qui di seguito sono
importanti soprattutto lo scheletro della funzione e le note.
16
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Implementazione in C:
typedef struct tnodo *ref; /* definizione di un tipo puntatore a tnodo */
typedef struct tnodo { /*definizione di un tipo di struttura tnodo */
int chiave,cont; /* qui cont sintetizza le informazioni e conta la
molteplicita’ della chiave inserita */
ref left,right;
};
Essendo definito un tipo puntatore a tnodo, l’ accesso alle variabili strutturate di tipo
tnodo avverra’ tramite puntatori di tipo *ref e quindi per accedere ai componenti
interni la struttura si usera’ l’ operatore freccia a destra ->; se invece un tipo puntatore
alla struttura non e’ definito, l’ accesso a variabili strutturate avviene tramite il loro
nome e si usa l’operatore punto tra il nome della struttura ed ogni componente interno
alla struttura.
Esempio: Albero Binario di ricerca & funzione Search_Insert di tipo ref:
6
/
4
\
8
/ \
/ \
2
5 7
9
struct tnodo *Search_Insert (int c, struct tnodo *p)
/* effettua la ricerca di c nell' albero puntato da p */
{
if (p == NULL) /* costruzione di un nuovo nodo */
{
p = (struct tnodo *) malloc(sizeof(struct tnodo)); /* N.B.
funziona anche senza il cast ma per pulizia concettuale e' bene metterlo! */
p -> chiave = c; p -> cont =1;
p -> left = p -> right = NULL; /*definizione completa */
}
else /* se c < nodo corrente, inserimento a sinistra, se no inserimento a destra */
if (c < p -> chiave) p -> left = Search_Insert( c, p->left);
else
if (c > p ->chiave)p -> right=Search_Insert(c, p->right);
else
p ->cont ++; /*chiave trovata: incremento del suo contat. */
return p; /*restituisce il puntatore al nodo inserito o trovato */
}/* fine Search_Insert*/
17
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
/* Si noti che la Search_Insert inserisce ogni nuovo nodo come foglia
l’ A.B. di ricerca cresce dalle foglie ! La Complessita’ della
Search_Insert e’ O(h) con h = altezza dell’ albero ed anche = numero di
attivazioni della Search_Insert stessa la funzione Search_Insert e’
attivata ricorsivamente con un SOLO richiamo per ogni attivazione. L’
innesco al processo ricorsivo e’ l’ attivazione del main: */
main() /* un esempio …*/
{
struct tnodo *root; /* puntatore al nodo
radice dell' albero */
int x;
/* chiave corrente */
printf("\n INIZIO CREAZIONE .... albero\n");
root = NULL;
do {
printf("\n Inserire la chiave =");
scanf ("%d",&x);
if (x != EOF) root= Search_Insert(x,root);
} while (x != EOF);
………/* continua */
/* Si noti il puntatore root usato 2 volte: la funzione
Search_Insert (int c, struct tnodo *p) usa p per scendere nell’ albero
dalla radice, ma se non trova la chiave cercata inserisce un nuovo nodo e
ne pone il puntatore in p restituendolo al programma chiamante (qui al
main) NON con p (che non e’ passato per indirizzo !), ma tramite il
nome della funzione stessa che lo assegna al puntatore da definire (qui
root).
Una volta costruito l’ albero si puo’ visualizzare con un’ altra procedura
ricorsiva: la visualizzazione comporta la visita dell’ albero che significa
accesso una ed una sola volta ad ogni nodo dell’ albero… QUINDI la
complessita’ e’ O( …) ?? */
………/* continua */
Print_tree(root,0);
printf("\n HO FINITO");
attendi();
} /* fine main */
18
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
void Print_tree(struct tnodo *p,int h)
/* Visualizza RICORSIVAMENTE le chiavi dell'
albero: ogni chiave e' spostata di h spazi dal
margine sinistro. SOLO per facilitare la visione
ruotata dell' albero di ricerca, qui per prima e'
chiamata
la
visualizzazione
destra.
Quale
complessita’ ?? */
{
int i;
if (p != NULL)
|
{
|
9
Print_tree (p -> right,h+1); |
8
for (i = 0; i<=h ; i++)
|
7
printf(" ");
|6
printf("%d\n", p -> chiave); |
5
Print_tree (p -> left,h+1);
|
4
}
|
2
}/* fine Print_tree */
|
STRATEGIE DI VISITA e Complessita’:
Visita INORDER:
Sin, Rad, Des; (ordine simmetrico)
“
POSTORDER: Sin, Des, R;
(postordine)
“
PREORDER: R, Sin, Des.
(preordine)
Come esempio: stampa ordinata: visita in ordine simmetrico
procedure stampa(a: pointer_alberobin); {Pascal}
begin
if a<>nil then
begin
stampa(a^sin);
write(a^.elem);
stampa(a^.des)
end
end;
Complessita’: per ogni attivazione 2 richiami: quindi ?
19
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Problema dei limiti di Complessita’:
vincolo sulla ristrutturazione dell’ A.B. di ricerca e
valutazione di:
an = lunghezza di ricerca in albero binario di ricerca
con n nodi equiprobabili,
mediata sulle n! forme possibili dell’ albero.
Risulta:
O (log2 (n)) an O (n)
Occorre definire limiti piu stretti.
Si ottiene:
lim an = 1.386 P i (n)
Significato: in media con n nodi equiprobabili la
lunghezza di ricerca media di un albero casuale supera del
39% quella del corrispondente Albero Binario
Perfettamante Bilanciato.
Conseguenza logica:
la Complessita’dell’algoritmo ristrutturante di un
albero casuale di n nodi
deve risultare < 0.39 P i (n)
Per valutare an si possono seguire 2 metodi:
definizione classica di albero e analisi matematicoprobabilistica che produce l’ espressione ‘classica’
an = 2 (n+1)/n Hn – 3
con Hn numero armonico di ordine n (cfr.appunti 1 pag. da Kruse);
definizioni ricorsive di albero, lunghezza-ricerca ..
e utilizzo di matematica elementare che produce
una espressione ricorsiva soddisfatta da quella
‘classica’.
Il risultato comunque si ottiene col
passaggio al limite dell’ espressione ‘classica’. …
20
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
21
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Valutazione di an = lunghezza di ricerca media di un Albero
Binario di n nodi di forma casuale.
Ipotesi:
n chiavi da inserire nell‘ albero binario di ricerca
numerate da 1 a n;
equiprobabili ossia: prob.(i=radice) = 1/n;
Procedimento per il calcolo di an ed il suo confronto con
P i (n):
1) Albero Binario di ricerca di radice i
ai
i-1
n-i
2) Valutazione di an(i) (ipotesi numerazione progressiva)
3) “
“ an
(epressione ricorsiva di tipo indiretto)
4) Formalizzazione di an = g (an-1)
5) Verifica che an cosi’ ottenuta e’ soddisfatta dalla forma
non ricorsiva che fa uso dei numeri armonici:
an = 2 Hn (n+1)/n – 3
con Hn=1+1/2+1/3+…+1/n =
= + loge n + 1/(2n) –1/(12n2) + ...
con: = 0.577216 (costante di Eulero) e
quindi: lim an ->loge n;
n->infinito
6) Passaggio al limite con il seguente risultato:
lim
an /
P i (n)
= 2 loge 2 (log2 n/ log2 n)= 1.38
n->infinito
22
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
1) Albero Binario di ricerca di radice i &
2) Valutazione di an(i) con l’ ipotesi della numerazione
progressiva delle chiavi
i
n
n
Ricordare: P i = (h’(i) pi) con
i=1
(pi) =1
i=1
i-1
prob.=(i-1)/n
n-i
prob.=(n-i)/n
ai-1 = lunghezza sotto_alb. sinistro
an-i = lunghezza sotto_alb. destro
an(i) = (ai-1 +1) (i-1)/n + 1/n + (an-i +1) (n-i)/n
Lungh. Ric. Media
sotto_alb. sinistro
Lungh. Ric. Media
sotto_alb. destro
1/n & (i-1)/n & (n-i)/n sono le probabilita’ della radice e
dei sotto_alb. = pesi
3) Valutazione di an (epressione ricorsiva di tipo indiretto)
ai-1 & an-i sono ottenute con lo stesso procedimento seguito
per valutare an ossia sommando le lunghezze degli alberi di
radice i moltiplicate per la probabilita’ che la radice sia i:
n
(*) an= an(i) (1/n)
i=1
an=(1/n)
n
{(ai-1 +1) (i-1)/n + 1/n + (an-i +1) (n-i)/n}
i=1
Si ottiene un’ espressione ricorsiva della lunghezza di
ricerca mediata sulle n! forme possibili dell’ albero con
prodotto fattoriale implicito che diventa esplicito dando alle
ai-1 & an-i le loro espressioni, per es. qui si e’sostituita ai-1 e supposto
a0=0:
n
i-1
an=(1/n) {([1/(i-1) ai-1(j)] +1)(i-1)/n
i=1
+ 1/n + (an-i +1)(n-i)/n}
j=1
23
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
n
La (*) an= an(i) (1/n)
i=1
appare come un’ espressione ricorsiva di tipo indiretto
an= f (an(i))
an(i) = F (ai-1, i, an-i)
con
quindi:
an = f ( F (ai-1, i, an-i))
4) Formalizzazione di an = g (an-1) ricorsione diretta !
Risulta:
n
an= (1/n) an(i) (1/n)
i=1
an(i) = (ai-1 +1)(i-1)/n + 1/n + (an-i +1)(n-i)/n =
= (1/n)[(i-1) ai-1 + (n-i) an-i + 1+ i - 1+ n - i] =
= (1/n)[(i-1) ai-1 + (n-i) an-i ] + 1
n
an= (1/n) {1+ (1/n) [(i-1) ai-1 + (n-i) an-i ]}=
i=1
n
=1+ (1/n ) [(i-1) ai-1 + (n-i) an-i ]
2
i=1
ma (i-1) ai-1 & (n-i) an-i danno lo stesso contributo
n
an= 1+ (2/n ) (i-1) ai-1= 1+ (2/n )
2
i=1
2
n-1
i ai
i=1
24
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
an= 1+ (2/n )
2
n-1
i ai = f (a1, a2,… an-1)
i=1
…ma come si arriva an= g (an-1) ? Si procede cosi’:
dalla an=1+ (2/n )
2
n-1
i ai
i=1
si estrae l’ ultimo addendo
an=1+ (2/n ) an-1(n-1) + (2/n )
2
2
n-2
i ai
i=1
parte A
parte B
e nella parte A si esprime an-1 tramite la f (a1, a2,… an-2)
an-1=1+ (2/(n-1) )
2
n-2
i ai
i=1
ottenendo:
(an-1-1) (n-1) = 2
2
n-2
i ai
i=1
Diviso tutto per n2 si riottiene a destra di = la parte B:
(1/n ) (an-1-1) (n-1) = (2/n )
2
2
2
n-2
i ai
i=1
an=1+ (2/n2) an-1(n-1) + (1/n2) (an-1-1) (n-1)2
parte A
nuova parte B
an=(1/n2)(n2 + 2n an-1 -2an-1+ n2an-1+ an-1 - 2n an-1 - n2-1+ 2n)=
= (1/n2){ an-1(n2-1) + 2n –1} = g(an-1)
25
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
5) Verifica che an= g (an-1) e’ soddisfatta dalla forma
non ricorsiva che fa uso dei numeri armonici:
an = 2 Hn (n+1)/n – 3
con Hn = 1+ 1/2 + 1/3 +……+1/n
Risulta:
an-1 = 2 Hn-1 (n/(n-1)) – 3 con Hn-1=1+ 1/2 + 1/3+..+1/(n-1)
an-1 =2 (Hn-1/n) (n/(n-1)) – 3 = 2 Hn (n/(n-1)) – 2/(n-1) – 3
Questa espressione di an-1si sostituisce nella g (an-1)
an= (1/n2){an-1 (n2-1) + 2n –1} si ottiene:
an= (1/n2){[2 Hn (n/(n-1)) – 2/(n-1) – 3] (n2-1) + 2n –1} =
= (1/n2){[2 Hn (n/(n-1)) – 2/(n-1) – 3] (n-1)(n+1)+ 2n–1} =
= (2/n)Hn(n+1) – (2/n2)(n+1) – 3(n2-1)/n2 + 2n /n2– 1/n2 =
=(2/n)Hn(n+1) +(1/n2)(-2n –2 - 3n2 +3 + 2n –1) =
=(2/n)Hn(n+1) –3 = 2((n+1)/n)Hn(n+1) –3
e si riottiene l’espressione classica !
6) Col passaggio al limite dell’espressione classica si
ottiene il risultato:
lim
an / P i (n) = 2 loge 2 (log2 n/ log2 n)= 1.38
n->infinito
26
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
CONCLUSIONI
Prima considerazione:
Complessita’ = funzione (Operazione Dominante)
In Alb. Bin. Operazione Dominante = Confronto
Lunghezza Ricerca Media = LRM =
= N.o di confronti medio = Cmedio (= funz(h) in A.B.Bilanciato)
Seconda considerazione:
log2 (n+1) LRM (n+1)/2
Alb. Bin. Perf. Bil.
Lista Lin.Ordinata
best_case LRM(h) worst_case
e… average_case ? Alb. Bin. a forma casuale = an
Si e’ dimostrato che:
lim
an = 1.386… log2 (n+1)
n
Deduzione logica: si deve ottenere che sia
Ripristino bilanciamento < 39% (log2 (n+1))
Ossia il Ripristino bilanciamento deve avere una
dipendenza da n di tipo logaritmico e NON lineare !
Quindi partendo da h=0 il Ripristino bilanciamento al
crescere di n deve seguire le variazioni di h NON di
n.
Gli Alb. Bin. AVL Bil. seguono questo comportamento e la
loro ristrutturazione e’ vicina al limite richiesto proprio in
base al teorema di Adelson-Velskii & Landis che fissa i
limiti dell’ altezza di un Alb. Bin. AVL Bil. di n nodi e ne
stabilisce il tipo di dipendenza da n (logaritmico).
27
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Teorema di Adelson-Velskii & Landis
log2 (n+1) hAVL(n) 1.4404 log2 (n+2) –0.328
h(Alb. Bin. Perf. Bil.)
max.h(Alb. Bin. AVL Bil.) (N.B.nel worst
case la costante moltiplicativa e' vicina a quella del limite superiore di complessita'
per l' algoritmo ristrutturante !)
best_case hAVL (n) worst_case
e… average_case ? hAVL (n) medio ?
Un problema ancora insoluto e’ proprio la valutazione
dell’ altezza attesa di un Alb. Bin. AVL Bil. di n nodi se
tutte le n! permutazioni delle chiavi da inserire nell’ albero
capitano con uguale probabilita’.
La risposta empirica ottenuta dall’ analisi di migliaia di
risultati e’:
hAVL(n) = log2 (n) + 0.25
Altro problema ancora insoluto e’:
con quale frequenza sono necessari i ribilanciamenti ?
La risposta empirica e’: in media 1 ribilanciamento capita
ogni 2 inserzioni ed ogni 5 cancellazioni nei rispettivi
algoritmi di Search_Insert e Delete. Dall’ analisi di
questi 2 algoritmi si vedra’ che: il modello AVL e’
valido soprattutto per ricerche. Quindi si deve
utilizzare se la frequenza di queste supera quella delle
inserzioni-cancellazioni … CASO PIU’ COMUNE.
28
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Alberi binari AVL bilanciati di n nodi: per ogni nodo
R risulta:
R
a
h(S)
h(D)
|bal| = |h(D) - h(S)| 1 bal = -1…+1
Situazioni ammissibili per ogni nodo:
a
a
a
a
a
a
a
a
a
a
Teorema di Adelson-Velskii & Landis
log2 (n+1) hAVL(n) 1.4404 log2 (n+2) –0.328
h(Alb. Bin. Perf. Bil.)
max.h(Alb. Bin. AVL Bil.)
a
Caso ottimo
Caso pessimo
Alb. Bin. Perf. Bil.
Alb. Bin. NON degenere
con altezza > 44% di quella
dell’Alb. Bin. Perf. Bil.
Si puo’ ottenere se:
Si puo’ ottenere se:
n e’ in {Ni} = insieme
di interi ottenuti dalla
sequenza di Fibonacci;
max. concentraz. nodi; min. concentraz. nodi;
min. altezza;
max. altezza.
n = 2h-1;
29
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Alberi binari AVL bilanciati pessimi: Alberi di
Fibonacci.
La forma: per una data altezza h, hanno il minimo
numero di nodi consentito per essere AVL bilanciati.
h
Tree #nodi normali
0
T0
0
1
T1
1
2
T2
2
3
T3
4 (3 produrrebbero: A.B.Perfett. Bilanc. o Lista Lineare)
4
T4
x (SS di h=3;Radice; SD di h=2)
quanto vale x ?
5
3
6
Si noti: ogni sotto-albero
2 4 7
e’ un alb. di Fibonacci !
1
Regola di produzione: Th = < Th-1 , R, Th-2 >
Nh = Nh-1 + Nh-2 + 1
E’ simile al principio di composizione di Fibonacci:
Fib(n) = Fib(n-1) + Fib(n-2) che
per n = 0,1,2,3,4,5,6, 7, 8, 9 ….
produce Fib(n) = 0,1,1,2,3,5,8,13,21,34….
La regola: Nh = Nh-1 + Nh-2 + 1 produce:
x=#nodi = 0,1,2,4,7,12…={Ni}, poco informativo, ma
confrontato questo insieme con quello di Fibonacci si
puo’ porre:
Nh = Fib(h+2) –1 espressione che produce lo stesso
insieme {Ni}: se e solo se n e’ in {Ni} l’ albero di n
nodi e’ di Fibonacci.
30
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Progettazione di un albero binario di x nodi:
1) Utilizzo del teorema AVL: metodo a)
2) “
della sequenza di Fibonacci: metodo b)
Avendo x nodi da porre in un albero binario si deve
considerare la hWorst: come valutarla?
1) metodo a):
si calcola:
hBest = log2 (x+1)
hWorst = 1.45 hBest
2) metodo b):
si ricorda che Nh= Fib(h +2) –1 ma la h ottenuta e’
la peggiore ossia: NhWorst = Fib(hWorst +2) –1
Posto: i = hWorst +2
risulta: NhWorst = Fib(i) –1
ossia: quando x = Fib(i) –1 hWorst = i-2
Generalmente accade che:
N(h1) < x < N(h2) ossia x sia compeso tra 2 valori
della sequenza di Fibonacci. In tal caso risulta:
h1 < hx < h2 (= hWorst)
i = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …
Fib(i) = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
Fib(i-2) produce una sequenza spostata a sinistra di 2
posti cosi’ per esempio a 10 corrisponde 144
Invece se x =130 risulta: 9 < hx < 10
31
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Alberi binari AVL bilanciati di n nodi: per ogni nodo
R risulta:
R
h(S)
a
h(D)
|bal| = |h(D) - h(S)| 1 bal = -1…+1
Alla creazione di ogni nodo bal = 0;
+1
in seguito alla creazione di figli bal={
-1
“ “
“ “
“ nipoti bal esce dal range.
Se nell’ albero AVL di radice R, prima di un’
inserzione a sinistra risultava:
caso1) hs < hd balR= +1 dopo hs = hd; balR=0 +okey
caso2) hs = hd balR = 0 dopo hs > hd; balR=-1 okey
caso3) hs > hd balR = -1 dopo hs>> hd; not okey e
RISTRUTTURAZIONE dell’ alb. considerando:
sottocaso 1
sottocaso 2
R (balR= -2)
R (balR= -2)
B (balB= -1)
A
(balA= 1)
A
B
LL rotation
LR rotation
Risultato
B
A
R
Discriminante tra i 2 sottocasi e’ il bal del figlio sinistro di
R che vale o –1 o 1.
Inserzioni a destra simmetriche: rotazioni RR, RL. Seguono esempi di LL
32
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Alberi binari AVL bilanciati di n nodi: ristrutturazioni
Importanti 2 aspetti:
a) la ristrutturazione deve conservare la caratteristica di
albero binario di ricerca;
b) salvare prima di tagliareprima di modificare un
puntatore salvarne il valore !
Si considerino le seguenti chiavi in arrivo: 4, 2, 1 che
producono
p
p
p
4
bal4=0
3
.
a
a
bal4=-1
bal2=0 2
4
a
bal4=-2
bal2=-1 2
bal1=0
4
a
1
a
LLrotation
…ma per ottenere l’ Albero AVL bilanciato:
p
2
4
a
1
a
NO:
p = p->left;// RICORDARE aspetto b) !!!
SI: ptemp = p->left;//ptemp ora punta 2. Salvato p->left si
p->left = ptemp->right;//ridefinisce ma punta sempre a chiavi <4
ptemp->right=p;//ptemp->right deve puntare a chiavi>2 aspetto a)
p = ptemp; // Nuova radice
Allo stesso albero si giunge se l’ ordine di arrivo delle
chiavi e’: 4, 1, 2 p
Per ottenere p
occorre
4
2
una RLrotation
a
+complessa
1
della LLrotation
a
e che richiede
2 puntatori di comodo.
1
a
4
a
2
33
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
struct tnodo *Search_Insert_Avl (int c, BOOL *h, p ref)
/* effettua la ricerca di c nell' albero puntato da p con h che diventa
TRUE se l’ altezza e’ cresciuta o comunque il bilanciamento e’ modificato:
scheletro simile alla funzione che non considera il bilanciamento */
{ /* inizio Search_Insert */ ref pcomodo, p2;
if (p == NULL) /* costruzione di un nuovo nodo */
{
p = (struct tnodo *) malloc(sizeof(struct tnodo)); /* N.B.
FUNZIONA anche senza il cast ma la pulizia concettuale lo impone !*/
p -> chiave = c; p -> cont =1; p ->bal=0; *h=TRUE;
p -> left = p -> right = NULL; /*definizione completa */
}
else // se c < nodo corrente, inserim. a sinistra e analisi di h
if (c< p -> chiave) p -> left = Search_Insert( c, h, p->left);
if (*h ==TRUE) // altezza sottoalbero a sinistra cresciuta ?
switch(p ->bal) { // inizio analisi dei casi con switch
case 1 : p ->bal =0; // bilanciamento migliorato
*h =FALSE; break;
case 0 : p ->bal = -1; //bilanciamento peggiorato *h resta True
break;
case –1: pcomodo = p->left; /* sbilanciamento: occorre
distinguere i sottocasi 1 e 2 con rotazioni LL e LR, ma
l’uso di almeno 1 puntatore di comodo e’ comune a entrambe le
rotazioni*/
if (pcomodo->bal ==-1)
{/*sottocaso 1: rotazione LL*/ p->left = pcomodo->right;
pcomodo->right = p;
p = pcomodo; }
else
{/* sottocaso 2: rotazione LR */ p2= pcomodo->right;
//…etc. etc. …fine rotazione LR }
p->bal = 0; *h = FALSE; break;
} // fine analisi casi con switch (continua a pag. seg.)
34
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
else // se c > nodo corrente, inserim. a destra e analisi di h
if (c>p ->chiave)p -> right=Search_Insert(c, h, p->right);
if (*h ==TRUE) /* altezza sottoalbero a destra cresciuta ?
situazione simmetrica a destra e rotazioni RR e RL
…*/
else
{ p ->cont ++; /*chiave trovata: incremento del suo contatore. */
*h = FALSE;}
return p; /*restituisce il puntatore al nodo inserito o trovato */
}/* fine Search_Insert */
Per la procedura Search_Insert in Pascal, completa di
entrambe le situazioni destra e sinistra: cfr. Wirth.
Il Numero di operazioni e’ poco superiore a quello
della procedura Search_Insert che non considera il
problema del bilanciamento
per le rotazioni LR o RL (caso peggiore) sono
necessarie 2 analisi e 8 assegnazioni in piu’.
35
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
La procedura di cancellazione di un nodo in alberi binari
di ricerca e’ un po’ piu’ pesante sia che consideri o no il
problema del bilanciamento.
A cancellazione avvenuta, l’ albero risultante deve essere
ancora un A.B. di ricerca. Per fissare le idee si consideri la
cancellazione nell’ A.B. di ricerca schematizzato:
LUIGI
BICE
D1
ADRIA
EVA
ADA
ALICE
JOB
ALBA
S1
NANDO
MARIA
PAOLO
MARA
NED REX
Sia p il puntatore al nodo da cancellare: si possono
verificare i seguenti casi.
Il nodo da cancellare:
1. e’ una foglia (per es. NED) p=NULL e il nodo
da cancellare si restituisce alla mem. libera. (Si
noti che nel caso di NED p era il left di PAOLO.)
#operaz. fatte =2;
2. ha un solo figlio (per es. MARIA) il figlio
sostituisce il nodo pcomodo =p; p=p->left e il
nodo puntato da pcomodo si restituisce alla mem.
libera.
#operaz. fatte =3;
3. ha per figli 2 sottoalberi sinistro S1 e destro D1
con:
Key(S1) < Key(nodo da cancellare) < Key(D1)
36
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
il nodo da cancellare si puo’ sostituire con quello
avente Key +grande tra tutte le Key minori (ossia
S1). Se per esempio si deve cancellare BICE si
puo’ sostituire con quello +a destra del sottoalbero
sinistro di BICE ossia con
ALICE = Key > {ADRIA…ALBA} && Key < {EVA…JOB}
#operaz. fatte = O(h(S1))
Per l’ implementazione descritta di seguito vale quanto
detto per la Search_Insert.
La Procedure Delete per A.B. qualunque e’nel Wirth in
Pascal (pag.211), quella per A.B. AVL bilanciati e’
analoga alla precedente, ma in piu’ utilizza le
rotazioni LL e RL per i ribilanciamenti. Questi
sono effettuati in 2 procedure separate; una per
ribilanciare il sottoalbero destro a causa di una
cancellazione nel sottoalbero sinistro, l’ altra per
ribilanciare il sottoalbero sinistro a causa di una
cancellazione nel sottoalbero destro: qui segue lo
schema della Delete in C per A.B. AVL bilanciati.
int rimuovi (struct tnodo **p,int chiave)
/* la function rimuovi cancella un nodo e restituisce il
parametro h (posto inizialmente False) che diventa True
quando l’ altezza cambia. NOTA: p passato per indirizzo*/
{ struct tnodo *q;
int h = 0; /*h diventera’ True quando l’ altezza
diminuisce*/
if((*p)==NULL )
{/* key not in tree*/
37
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
h = 0;
printf("\nLa chiave non c'e' albero vuoto? %d"\n, chiave);
return h; /*se era stato il main ad aver attivato la function*/
}
/* con: h=rimuovi(&root, key); avra’ di ritorno h=False */
else
{ if (chiave < (*p)->chiave)
{
if (rimuovi (&((*p)->left),chiave))
h = bilancia_des (&(*p));/*le rot. RR e RL */
}/*possono porre h=False */
else
if (chiave > (*p)->chiave)
{ if (rimuovi (&((*p)->right),chiave))
h = bilancia_sin (&(*p));/*le rot. RR e RL */
}/*possono porre h=False */
else
/*cancella(*p) */
{ q = (*p);
if ((q->right)== NULL)
{
(*p)= q->left;
h =1; /* e’ in atto una */
} /*cancellazione con possibile diminuzione dell’ altezza*/
else if ((q -> left)== NULL)
{
(*p)=(*p)-> right; h=1;/*e’ in atto … idem */
}
else {del(q->left,&h); /*la proc. del ritorna *h=True */
if (h) h = bilancia_des (&(*p)); } /* le rotaz. LL e LR*/
}
/*
possono porre h=False */
}return h ; /* rimuovi ritorna il valore calcolato di h */
}
int bilancia_des (struct tnodo **p)
/*ribilancia' il sottoalb. destro e restitusce il valore di h
(posto inizialmente 0)*/ return h;}
38
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
int bilancia_sin (struct tnodo **p)
/* ribilancia il sottoalb. sinistro e restitusce h */{ int
h=0; /* ……………*/ return h;}
void del (struct tnodo *q, int *h)
/* simile alla del (Wirth pag.211) senza ribilanciamento
con in piu’ *h=1 attivata solo nel caso 3 (il nodo da
cancellare ha come figli 2 sottoalberi S1, D1) */
{… *h=1; …
}
Riflessioni:
sulle motivazioni delle strutture dinamiche ?!
…ormai assodate! sulla convenienza dell’ uso
di Alb. Bin. di ricerca rispetto alle liste lineari ?
appaiono dall’ organizzazione dell’ Alb. Bin. di
ricerca derivata dal procedimento dicotomico di
Newton-Rapson per la ricerca delle radici di equazioni
quadratiche in un dato intervallo x
2 suddivisioni ricorsive che producono un tempo di
ricerca = O(log2x);
sulla possibilita’ dell’ uso di Alb. Bin. di
ricerca AVL Bilanciati per
memorizzare
informazioni su memorie secondarie (disco) …
Memorie secondarie: tempo di accesso 5 ordini di
grandezza maggiore di quello per la C.M.
necessita’ di altri modelli che si introducono nel modo
seguente.
39
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Dal procedimento dicotomico si passa al
procedimento kappa-tomico che consiste nel
considerare k classi di ripartizione dell’ intervallo x e
considerarle non sequenzialmente, ma con un’
organizzazione che emuli una elaborazione
parallela in modo da ottenere il termine cercato con
un tempo di ricerca = O(logkx).
Le K suddivisioni non devono porsi sequenzialmente
ossia NO:
-> |_____| -> |_____| -> |_|_|_|_|_| -> |_____| -> |_____| ->
ma:
|_____________|
|______| |______| |_|_|_|_|_|_|_| |______|
…
|______| |______| |______| |______| |______| |______|
Teoricamente il modello Alb. Bin. AVL-bilanciato si
puo’ usare per memorizzare un file su disco; in pratica
no.
Motivazione: parlando di file si cambia dimensione
non+ decine di record (un migliaio al +), ma migliaia
o milioni di record.
Si pongono 2 problemi:
1. (principale) tempo di risposta nella ricerca di 1
record di data chiave. Per gli Alb. Bin. AVL
risulta:
hAVL(n) < 1.44 (log2(n+2)-0.328
se n = 1 000 000 allora log2(n) = 20
40
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
20 hAVL(n) 29
P = CMedio= O(h) ossia “mediamente” con 29
accessi all’ Alb. Bin. AVL-bilanciato di
1 000 000 di nodi si ottiene il record cercato
ragionevole in C.M.
t = F( P ) {
esagerato in memoria di massa
L’ utilizzo di memoria di massa richiede una
riduzione di h !!
Albero a molti rami che pero’ sia bilanciato
ossia non degeneri in lista lineare.
Es. 1 000 000 di termini puo’ stare in 10 000
nodi con 100 termini/nodo: se si usa solo
1ramo/nodo allora h=10 000; ma se si usano
100rami/nodo allora h = 3 = log100(1003).
2. Sfruttamento del disco organizzato a blocchi o
pagine 1 blocco (>> cella di C.M.) = quantita’
di informazioni accessibile con una sola operazione
di I/O.
41
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Albero ottonario con Alb.Bin.perf.bil. come sotto-struttura appunti da
precedenti dispense: 1pagina.
42
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
43
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Introduzione ai b-alberi o alberi b dove b sta per balanced:
modello di Bayer-McCreigth 1970
Esempio:
b-albero paginato di ordine k=2 e altezza h=3
n.ro pagine = 11 (alcuni termini inutilizzati sono omessi)
grado di riempimento 27/44 = 60%
N
DHK
ABC
EFG
I J
Q SW
LM
OP
R R1
T UV
XY Z
Visita: inorder ordinamento ascendente delle chiavi
Ricerca: con 3 accessi al b-albero si puo’ rispondere se la
chiave e’ presente
Caratteristiche: lucido seg. ma gia’ da qui si vede che l’
organizzazione e’ simile a quella degli Alb. Bin. di
ricerca.
44
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Definizione di b-tree di ordine k ed altezza h con:
k 1 e h 0.
Dati h e k un albero T e’ un b-albero (b=bilanciato) se
e’ vuoto o gode delle seguenti proprieta’;
1. ogni nodo (=pagina) che non sia foglia (terminal
node) ne’ radice ha almeno k+1 figli e k termini;
2. ogni pagina che non sia foglia ha al piu’ 2k+1 figli e
2k termini;
Da 1. e 2. k+1 n. ro figli/pagina 2k+1
k n.ro termini/pagina 2k
3. la radice, se non e’ foglia ha almeno 2 figli ed 1
termine;
4. tutte le foglie sono allo stesso livello e non hanno
figli;
5. qualunque pagina non foglia con m termini ha m+1
figli.
Es. di b-albero di ordine k=2 e altezza h=3 dove per la
radice 2 n.ro figli 5
per le altre pagine 3 n.ro figli/pagina 5
25
30 40
10 20
5 7 8 9 13 15
21 24
27 28
32 38
41 50
45
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
REALIZZAZIONE di b-albero di ordine k (con 2*k
+1 "RAMI" al piu’) e denotazioni in PASCAL e in C
dove le indicazioni in corsivo sono in piu’ e il b-tree e’
di ordine 2:
const k =...;
#define PAG_ELEM 4 /*2k*/
type elem = record
#define MIN_ELEM 2 /*k*/
chiave : integer;
#define MAX_PAGINE 50 /*buffer!*/
p :^page;
typedef struct page *tpage;
{ altri campi, per es. info: integer }
struct elem /* = record */
end;
{ int chiave, info; tpage p ;};
page = record
struct page
p0:^page;
{ int cont; tpage p0;
e : array[1..2*k] of elem;
struct elem e[PAG_ELEM] ;
end;
} * pagina [MAX_PAGINE] ;
#define DIM_PAGINA (sizeof(struct page))
Un termine ti (di tipo elem) e’ una terna:
{ chiavei ,infoi ,pi }
con i = 1… 2*k e infoi = informazione associata alla
chiavei;
pi = puntatore associato alla chiavei e Struttura della
pagina (page) di 2*k termini:
p0 t1 t2 ……… t2*k
Eventuali
contatore punt.padre
Considerazioni:
la struttura ordinata di pagina dipende dal fatto
sostanziale che ogni insieme di termini in una
pagina e’ un sottoalbero dell’ albero binario di
ricerca che e’ la struttura di base del b-albero;
46
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
una volta letta la pagina in memoria, l’ ordinamento
dei termini al suo interno facilita il metodo di ricerca
di una chiave: (tabelle ordinate ricerca binaria.)
Legge tra chiavi e puntatori:
in page puntata da p0 devono trovarsi le keyj < key1
in page punt. da p1 sono le key y con: key1< y< key2
in “
“
“ p2 “
“ “ z “ key2< z< key3
……..
in page punt. da pm sono le key w con: keym < w
Questa legge condiziona l’ algoritmo di ricerca di un
dato termine.
Algoritmi di search, insert per b-alberi: appunti 2 pag.
da dispense precedenti e…
47
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
48
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
…e da Acta Informatica.
49
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Insert per b-albero di ordine 2: operazione split
addr.=700
10
101
20
102
12 4 9
5
30
103
11 12 13
23 26 28
25
104
31 32 35
25 viene inserito nella pagina 103 senza problemi, che ci sono
invece per l’ inserimanto di 5 nella page con
1 2 4 5 9. Sono troppi 5 termini quindi SPLIT di pagina:
si alloca una nuova pagina (di addr.=105) e vi si spostano
i 2 termini oltre il mediano ossia quelli con chiave 5 e 9;
il mediano si sposta nella pagina padre: si ottiene
4 10 20 30
101
12
105
5 9
102
11 12 13
103
23 25 26 28
104
31 32 35
. .. ma dovendo inserire anche
21
21 23 25 26 28 provocano un altro split che puo’
propagarsi fino alla radice. Come prima:
si alloca una nuova pagina e vi si spostano i 2 termini
oltre il mediano ossia 26 28;
il mediano 25 si sposta nella pagina padre che pero’ ora
e’ gia’ piena. Quindi si considerano i 5 termini:
4 10 20 25 30, si alloca una nuova pagina ove si spostano
i 2 termini oltre il mediano ossia 25 30; allocata una
nuova pagina radice vi si sposta il mediano 20 con un
puntatore p0 alla vecchia radice (contenente ora 4 e 10)
ed un puntatore p1 alla pagina appena allocata con 25 e
30.
50
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
N.B. Lo split ed il merge si propagano dalle foglie alla radice. I
b-tree crescono dalla radice e dalla radice anche decrescono per
effetto di cancelleazioni successive.
Algoritmo
di
delete:
Informatica.
da
Acta
51
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Comunicazione! A BREVE uscirà un BANDO relativo ad
una
BORSA DI STUDIO E PREMIO DI
LAUREA
per lo
SVILUPPO DELL’EDILIZIA
CIMITERIALE A TRIESTE
promosso da
Il Comune di Trieste, con il contributo della
Fondazione CR Trieste
….
Con riferimento al settore informatico viene istituito
un progetto di ricerca finalizzato alla redazione di
una tesi di laurea sulla realizzazione di:
“Strumenti multimediali rivolti all’ analisi
del territorio e della storia degli
insediamenti cimiteriali esistenti a Trieste”
REGOLAMENTO
1.Possono partecipare al concorso gli studenti che siano
iscritti ad un corso di Laurea dell’ Università degli
Studi di Trieste e che siano in predicato di sostenere la
propria tesi di Laurea in Ingegneria Elettronica o
Informatica. Il progetto di ricerca relativo alla stesura
di quest’ ultima, deve essere sviluppato dallo studente
in accordo con il docente relatore della tesi stessa.
…..
52
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
TENERSI INFORMATI !!!
La cancellazione di un termine su una pagina non foglia
(per es. 20) comporta le 2 alternative seguenti:
100 200
alternativa 1
20 50 70
alternativa 2
5
13
.1.2.3.4. .7.9. .14.15.17.
25
37
.22.23.24. .30.32. .39.40.
e produce (con alternativa 1) il risultato seguente:
100 200
17 50 70
5 13
.1.2.3.4. .7.9. .14.15.
25
37
.22.23.24. .30.32. .39.40.
In fase di cancellazione (o anche meglio prima) si puo’ far
scattare un algoritmo di catenazione (tra 3 pag.) per
compattare termini e cercare di evitare eventuali merging
che si propagano. La catenazione puo’ essere attivata anche
in fase di inserzione per evitare lo splitting ed il suo
propagarsi. Catenazione & merging sono 2 procedure che
53
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
scattano in tempi diversi, ma entrambe producono la
fusione di pagine.
Delete per b-albero di ordine 2: operazione di merging
1 5
8 11
9 10
13 15
Cancellando 5 la pagina piu’ a
utilizzata: non puo’ stare in tale
merging con la pagina “sorella” ed
si hanno 4 chiavi: 1 8 9 10
pagina ottenendo:
sinistra diventa sottosituazione. Occorre un
il termine “padre”. Qui
possono stare tutte in 1
11
1 8 9 10
13 15
Poiche’ 8 e’ scesa di 1 livello sono scesi anche l’ info e il
puntatore associati (questo viene ridefinito a 0) e
1 8 9 10 viene puntata dal vecchio p0 .
Se a questo punto si cancellano 1 8 e 13 le quattro
chiavi restanti con un merging si pongono tutte in radice
che diventa:
9 10 11 15 ed e’ radice e foglia insieme !
Il modello b-tree presentato segue la definizione di Wirth,
esiste però un altro modello di Knuth presentato nel luc.
seguente (1 pagina del Knuth).
Proprio lui 1972 fissava il range dei valori di k tra 64 e 128
per avere un numero limitato di accessi al disco con file
aventi 200 M di termini come e’ detto nel lucido
54
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
seguente (vedere Caratteristiche riassuntive dei b-tree
3.+ 4. )
55
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Caratteristiche riassuntive dei b-tree:
56
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
1.
possono degenerare in lista lineare ? NO! Un b-tree di ordine
k alla peggio diventa un albero a k+1 rami che se k=1 e’ un b-tree di
ordine 1 (cfr. lucidi 63 - 67…).
2.
e’ possibile la scansione sequenziale-selettiva dei
termini? SI! Scansione sequenziale: visita del b-tree in modo
simmetrico; scansione sequenziale-selettiva: utilizzo degli indirizzi di
pagina, dell’ ordinamento dei termini nella pagina … ed anche utile il
puntatore al padre!
3.
l’ algoritmo di search ha 2 ordini di grandezza search
di pagina e search di chiave, che pero’ e’ realizzato in C.M. ed e’
trascurabile rispetto al precedente importante e’ ridurre il numero
di accessi al disco ossia l’ altezza del b-tree occorre aumentare il
#termini/page ?! vedere considerazioni 3+4 !
4. nell’ algoritmo di insert lo split e’ propagato verso l’ alto
fino alla radice;
5. nell’ algoritmo di delete il merge e’ propagato verso l’
alto (anche fino alla radice) come appare dall’ esempio di
b-tree con k=2 e h=3:
9 20
3 6
13 16
23 35
1 2 4 5 7 8 …
…
Cancellazione del termine di chiave 1 sottoutilizzo della
page che aveva 1 2 merging con il termine “padre” 3 e
la page sorella con 4 5 2 3 4 5 in una sola page, ma
sottoutilizzo della page che aveva 3 6 merging con il
termine “padre” 9 e la page sorella con 13 16 …
3.+ 4. negli algoritmi di insert (e di delete ?), in C.M.
sono necessari h+1 buffer (ciascuno di dimensione pari alla
page) per lo split (e il merge ?) tanti quanto e’ lungo un
percorso di ricerca +1 per l’ eventuale inserzione di una nuova
radice PESANTE ! e condizionante la dimensione della page !
(Ricordare limiti per k di Knuth !)
57
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Attenzione ! Necessaria ridristribuzione a scadenze &
conoscenza del legame tra h e k. La ridristribuzione dei termini
all’interno di un b-tree di ordine k e’ realizzata col seguente processo di
catenazione:
siano 2 pagine adiacenti P(pi-1) e P(pi) contenenti meno
di 2k termini per effetto di cancellazioni senza il merging
successivo;
sia Q la pagina padre con almeno k+1 entry tra cui:
... (key i-1, pi-1) (key i, pi) (key i+1, pi+1) …
In queste condizioni i termini delle 2 pagine P(pi-1) e P(pi)
col termine “padre” Q si possono porre nella sola pagina
puntata da pi-1 mentre pi puo’ venire ridefinito.
La catenazione si puo’ usare a scopo di ridristribuzione
dei termini anche in condizioni non di sottoutilizzo, ma di
un certo “sbilanciamento” dei termini (indicato dai
contatori di pagina, per esempio utilita’ dei contatori!!)
con accumulo dei termini in un sotto_b-tree dove per es.
ogni contatore fosse =2*k ed invece in un adiacente
sotto_b-tree si avessero condizioni di minimalita’ (ogni
contatore =k). In questa situazione la ridristribuzione puo’
evitare casi di sottoutilizzo (underflow di pagina) e
soprautilizzo (overflow di pagina) NON si propaga !
Nell’esempio precedente prima di possibili cancellazioni una
ridistribuzione dei termini di chiave da 1 a 9 poteva dare il b-tree:
20
5
13
16
1 2 3 4 6 7 8 9 …
23 35
… …
lasciando in radice un solo termine e ponendo quello di chiave
mediana 5 nella pagina padre delle due foglie piene: cosi’ la
cancellazione del termine di chiave 1 non avrebbe prodotto altri
effetti… ridistribuzione “su misura”!
58
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
B-tree di ordine k e altezza h: legame tra h e k dedotto da
kmin= #min. di termini ad ogni livello
kmax= #max. di termini ad ogni livello
Livello #min. page
Kmin
#max. page
1
1
1
1
2
2
2k
2k+1
3
2(k+1)
2(k+1) k
(2k+1)2
4
2(k+1)2 2(k+1)2 k
(2k+1)3
…
i
2(k+1)i-2 2(k+1)i-2 k
(2k+1)i-1
…
h
2(k+1)h-2 2(k+1)h-2 k
(2k+1)h-1
kmin Tot = 1 + 2 k (
h-2
kmax
2k
2k (2k+1)
2k (2k+1)2
2k (2k+1)3
2k (2k+1)i-1
2k (2k+1)h-1
(k+1)i ) =
i=0
= 1+ 2k ( (k+1) h-1 -1)/(k+1-1) = 2(k+1) h-1 –1
(kmin Tot +1)/2 = (k+1) h-1 logk+1((kmin Tot +1)/2) = h-1
kmax Tot = 2 k (
h-1
(2k+1)i ) =
i=0
= 2k ( (2k+1) h -1)/(2k+1-1) = (2k+1) h -1
kmax Tot +1 =(2k+1) h log2k+1(kmax Tot +1) = h
Posta n la cardinalita’ dell’ archivio da inserire nel b-tree
kmax Tot = kmin Tot = n
log2k+1(n+1) h logk+1((n+1)/2) +1
59
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Progetto con valutazione delle prestazioni dei b-tree.
Data la legge:
log2k+1(n+1) h logk+1((n+1)/2) +1 che fornisce il
legame tra h e k, per definirne i parametri occorre
stabilire le priorita’ su cio’ che interessa di +.
1. +importante sia limitare il numero di accessi al
disco per es. porlo 3
h logk+1((n+1)/2) +1 3
logk+1((n+1)/2) 2
(n+1)/2) (k+1)2
(n+1)/2) (k+1)
e quindi dedurre il valore di k (se per es. si ha
n = 2*104 k = 99)
2. +importante sia limitare l’ uso della C.M.
imponendo per es.
max.dimensione/page = 2k = 60KB
h log31((n+1)/2) +1
e quindi dedurre il valore di h: se per es. si ha
n = 31249 log31(15625) = 2.8 h 4
e il totale della C.M. necessaria vale:
2k(h+1) 300KB
La dimensione della page dipende da:
60
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
n. ro page da porre contemporaneamente in C.M. e
per questo valgono le considerazioni fatte al punto
3.+4. del lucido 48;
dimensione del termine che e’ fondamentale.
Dimensione page - dimensione termine:
schematizzando il termine con la chiave si assume
implicitamente che il termine sia di dimensioni limitate,
altrimenti la dimensione del termine puo’ porre un altro
limite al valore di k che deve essere ridotto.
Sorge l’ obiezione: riducendo k si avra’ un aumento di h e
del numero di accessi al b-tree ossia al disco …
La giusta obiezione fornisce l’ innesco al processo di
modifica del modello originale che produce altri modelli
analoghi, ma piu’ “snelli”.
Il b-tree e’ un modello di struttura che si presta a
memorizzare archivi con record brevi, ma il record +breve
e’ quello formato dalla sola chiave che lo identifica
se si sceglie di memorizzare i record completi solo
nelle pagine foglie e nelle altre solo le chiavi con i
puntatori associati, si avranno 2 formati diversi per le
pagine foglie e per quelle intermedie.
Si ottiene un modello derivato dal b-tree che puo’ essere
un B*tree o un B+tree, 2 varianti del b-tree nei quali le page
non foglie contengono i “riferimenti” ai record. Questa
funzione di riferimento e’ quella svolta da un indice =
=f(A, B) che associa 2 entita’ A e B che possono essere la
chiave del record (A) ed il suo indirizzo (B).
Si deduce che i B*tree ed i B+tree sono adatti a
memorizzare file con indice o file indexati.
Il modello file con indice e’ ben posto da Wirth come indicato di seguito.
61
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Modello teorico di file indexato di Wirth
(da N. Wirth
“Algorithm + Data Structure =Programs”, pag.39-40: Index File in Pascal.)
type unitrecord = record …. end;
T0 = file of unitrecord;
T1 = file of T0;
T2 = file of Ti;
….
Ti = file of Ti-1;
…
struct unitrecord {…};
typedef FILE *T0;
typedef FILE **T1; ?!
T0 realizzabile fisicamente tramite un buffer di tipo
unitrecord (in C unitrecord sara’ una struct)
T1 come si puo’ implementare ? bufferT1 di quale tipo
e’? di tipo T0 ? ma il tipo T0 e’ un file sequenziale
quindi con cardinalita’ indefinita, variabile …
Modello di implementazione:
una variabile di tipo T0 e’ dinamica e quindi trattabile
come le variabile dinamiche tramite il meccanismo dei
puntatori ossia con indirizzamento indiretto anche a piu’ livelli;
la cardinalita’ di un file varia nel tempo: al tempo
t=t1 una variabile S di tipo T0 (il tipo Pascal si indica con :)
avra’ una cardinalita’ definita, VALUTABILE. La
variabile S viene detta Segmento, IndSeg e’ il suo
puntatore ossia:
var IndSeg = ^ T0; {^ indica il puntatore in Pascal};
una variabile X di tipo T1 si puo’ allora rappresentare
al tempo t=t1 come una sequenza di puntatori a var. S: T0
X ={ IndSeg1, IndSeg2, … IndSegi}
Ossia X e’ un file indexato ad un solo livello con
modifiche effettuabili nella sequenza di indirizzi e nelle
variabili di tipo T0: ripetendo il ragionamento per Y di
tipo T2 si otterra’ un file indexato a due sottolivelli … e
cosi’ di seguito.
62
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ oggetto X avra’ la forma seguente:
|IndSeg1| IndSeg2| …. |IndSegi|
|____| |____|
|____| |____|
|____| …
…
|____| |____| |____|
|____| |____| |____|
|____| |____| |____|
|____| …
|____|
|____|
… .
Le frecce verticali ed orizzontali indicano possibilita’ di
incremento e decremento dei file S : T0 e della sequenza
di puntatori si ricordi che si tratta di file non di
tabelle !!
(Si notino 2 tipi di elementi: i puntatori ed i file !)
L’ oggetto X di tipo T1 sara’ il primo componente di Y di
tipo T2 file indexato a 2 sottolivelli … e cosi’ di seguito.
Modello b*tree
variante del modello b-tree con 2 formati per le pagine a
secondo che si tratti di pagine foglie e non foglie.
Max. formato di pagina NON foglia di un b*tree di
ordine k:
p0 key1 p1 key2 p2 ……… key2*k p2*k
dove p0 punta ad un sotto-b*tree con keyj < key1
p1 punta ad un sotto-b*tree con key1 keyj < key2
p2 punta ad un sotto-b*tree con key2 keyj < key3
…
p2*k punta ad un sotto-b*tree con key2*k keyj
Si notino le ripetizioni di chiave (sotto-alberi p1^, p2^,…) dovute
alle disuguaglianze deboli che nel b*tree sostituiscono a sinistra le
disuguaglianze forti del b-tree.
63
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Max. formato di pagina foglia di un b*tree di ordine k:
(key1 inf1) (key2 inf2) ………(key2*k inf2*k) ?punt.sorella
dove il puntatore alla pagina foglia adiacente (sorella) e’
opzionale.
Esempio:
non foglia
17 50 70
foglie
5 inf5 13 inf13
inf17inf17 inf17
inf13
Modello
b+tree
17 inf17 23 inf23 39 inf39
inf23 inf23 inf23
iinf23inf23inf39
25 37
altra variante del modello
b-tree con struttura della
pagina foglia uguale a quella dei b*tree: le foglie
possono essere collegate tra loro in lista lineare
doppia.
Struttura della pagina non foglia puntatore p0
eliminato e ogni altro pi e’ associato alla chiave “sua” keyi ,
nel senso che ogni chiave keyi e’ la +grande tra quelle
contenute nel sotto-b+tree puntato dal puntatore pi;
la radice contiene almeno 2 chiavi.
L’ esempio mostra le pagine del precedente b*tree collegate
in un b+tree
non foglia 17 50 70
foglie
23 inf23 39 inf39 50 inf 50
inf50
Il b+tree rispetto al b*tree ha
analoghe. Rispetto al b25 prestazioni
37
tree l’ elaborazione sequenziale-selettiva e’ migliore per i
collegamenti delle foglie, peggiore e’ la ricerca del singolo record.
5 inf5 13 inf13 17inf 17
64
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Un indice (breve con meno di 1000 voci) si puo’ realizzare
in C.M. con un albero binario AVL bilanciato o con un btree di ordine k=1 (binary b-tree: bb-tree).
SI TRATTA DI B-TREE e quindi vale:
log2k+1 (n+1) hbb 1+ logk+1 ((n+1)/2)
log3 (n+1) hbb 1+ log2 ((n+1)/2)
log3 (n+1) hbb 1+ log2 (n+1) - log2 2
log3 (n+1) hbb log2 (n+1)
Confronto immediato con modello albero binario AVL bilanciato
log2 (n+1) hAVL 1.4404 log2 (n+2) –0.328
Essendo:
log3 (x) < log2 (x) & log2 (n+1) < 1.4404 log2 (n+2)
risulta: il range di variabilita’ per l’ altezza dei bb-tree e’
+piccolo, spostato verso il basso con limite superiore
+piccolo hbb< hAVL
Pero’ per la lunghezza di ricerca media risulta:
Lmedia-AVL < Max. Lbb
Perche’? Dipende dalla struttura della pagina (nodo) del bbtree contenente 2 termini: per trovare la pagina ed il
termine cercato occorre fare 2 confronti per ogni pagina.
Essendo tutta la struttura in C.M. non ci sono diversi ordini
di grandezza per la ricerca di pagina e la ricerca del termine.
Quindi la lunghezza di ricerca Massima nei bb-tree e’
proporzionale a 2*hbb mentre le lunghezze di ricerca medie
risultano:
Lmedia-AVL = Lmedia-bb= O(h) = O(log2 (n))
65
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
almeno 1 termine e 2 puntat.
Page(b-tree di k=1)
{
fino a 2 termini e 3 puntatat.
In C.M. non e’ ammissibile la perdita del 50% quindi
per la page non va bene una tabella, ma una lista di 1 o
al piu’ 2 termini.
tabella
“
Primo modello: lista a destra
termine = {key, info,left, h, right }
1 se puntatore right orizzontale
con h = {
0 “ “
100 -----------> 200
h=1
h=0
a
a
“ verticale
a
lista
100
key<100 100<key<200
200<key
Risulta: asimmetria di trattamento nelle inserzioni a
destra e a sinistra
66
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Siano da inserire:
a destra A e B:
a sinistra B e A:
A
B
B
A
a destra B puo’ diventare fratello destro di A salendo a
livello superiore, ma a sinistra A non puo’ diventare
fratello sinistro di B ...
ASIMMETRIA di trattamento
Altro Modello.
Si noti come lo split e la catenazione tra pagine sorelle
dei b-tree si ripropongono nei bb-tree in forma
particolare.
67
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Secondo modello:
SBB-tree: Symmetric Binary B-tree (Bayer ’72):
entrambi i puntatori possono essere orizzontali o
verticali
termine = {key, info, lh, left, rh, right }
lh, rh: 2 variabili booleane con significato:
TRUE il termine ha un fratello
FALSE “ “
non ha “
Situazione di split: 3 fratelli sullo stesso livello
ossia 2 puntatori orizzontali (a sinitra e/o a
destra).
SBB-tree = hedges (siepi) nome che deriva dalla loro
crescita come appare dalla fig. 4.53 di Wirth.
Alla classe degli hedges appartengono gli AVL_tree e
vale:
Lmedia-AVL < Lmedia-hedges
Pero’ le ristrutturazioni sono meno frequenti negli
hedges: quindi questi sono preferiti specie per ricerche
come avviene negli indici brevi realizzati in C.M.
Esempi di Inserzioni negli hedges: 1 pagina dal
Wirth con la fig. 4.53.
68
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
69
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Modello Alberi Binari Ottimi
Tornando a parlare di strutture in C.M. occorre
considerare anche questo modello utile nel caso in cui
l’ ordinamento delle chiavi non e’ di tipo alfabetico
ne’ numerico crescente o decrescente.
Si introduce con la seguente analisi semplificata
L’ algoritmo di costruzione di Alb. Bin. di Ricerca
di n nodi inserisce il nuovo nodo come foglia si
hanno inserimenti a livello 1 (radice) 2, 3 … h
Prima di ogni inserimento e’ necessaria la ricerca
il nodo e’ gia’ presente nell’ Albero ? e si
ottiene: P i = O(h) = O(log2 n) se h = log2 n.
Un’ alternativa costruire una tabella di n
elementi disordinati e poi ordinarla con un
algoritmo di sort interno efficiente Complessita’
= O(nlog2 n).
Fin qui: n.ro operazioni necessarie nei 2 casi ~
uguale.
Se pero’ occorrono altri inserimenti (per es. altri m
inserimenti) si ha:
nell’ Albero:
n. ro operazioni m log2 (m+n)
nella Tabella, inserendo in fondo e poi ordinando:
n. ro operazioni (m+n) log2 (m+n)
70
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Si giunge alla solita conclusione qui ribadita in
modo +elementare: se la struttura non e’ soggetta a
modifiche frequenti assomigliando ad una struttura
statica
e’ valido il tipo Tabella; altrimenti
e’ valido e +conveniente il tipo Ab. Bin. di
Ricerca, ma con h = log2 n.
Dall’ analisi semplificata si deduce che la tabella
delle chiavi ordinate, diventa un modello alternativo
all’ albero binario di ricerca se e solo se il numero
di cancellazioni ed inserzioni e’ vicino a 0; va
anche bene se le inserzioni sono poco frequenti con
intervalli lunghi (annuali) tra una e l’ altra.
Questo e’ il caso delle parole chiave di un
compilatore.
Gli aggiornamenti su queste sono poco frequenti o
nulli per lunghi periodi
per le parole chiave di un compilatore va bene un
modello statico tipo la tabella ordinata;
la funzione d’ ordine pero’ deve essere scelta sulle
frequenze di accesso a tali parole.
Cio’ si ottiene col modello albero binario ottimo.
Si tratta di un modello alternativo all’albero binario
di ricerca valido come lo e’ la tabella ordinata quando
cancellazioni ed inserzioni tendono a 0 “nel tempo” o
anche la loro frequenza tende a 0.
71
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Caso tipico di questa situazione si ha con le parole
riservate di un linguaggio artificiale aggiornamenti
su esse 0
Un modello statico sembra +adatto per memorizzarle.
Quale ? NO tabella ordinata in ordine alfabetico
Es. avendo 3 parole riservate del C come:
function, goto, if
se si inseriscono in ordine alfabetico in una tabella o
in A.B. di ricerca risulta:
root
goto
function
if
Il privilegio della radice e’ per goto che non dovrebbe
essere mai usato … SI tabella o A.B. ma la
funzione d’ ordine deve usare la frequenza di
accessoAlbero Ottimo
Altro esempio: 1 pag. da Knuth con es. per parole
inglesi.
72
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
73
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Alberi Binari Ottimi o Ottimali nel senso della ricerca.
“Alberi” binari di ricerca la cui forma dipende dalla
frequenza d’ accesso delle chiavi poste nei nodi
dell’ “albero” non e’ detto che si ottengono alberi
bilanciati!
la forma e’ scelta in base alle frequenze d’ accesso
ai nodi che devono essere note (in generale non lo
sono !)
intuitivamente il criterio di costruzione e’ il
seguente:
la chiave +spesso interrogata va in radice; nei nodi
interni vanno le chiavi con frequenza intermedia;
le chiavi –spesso interrogate vanno nelle foglie;
Però il modello usato nella costruzione è l’ “albero”
binario esteso in quanto occorre considerare anche
le ricerche che portano a nodi esterni (identificatori
non chiavi) ricerche di chiave con e senza
successo;
Motivazioni:
Le chiavi e le loro frequenze d’ accesso sono note in
partenza: non aumentano ne’ diminuiscono, la loro
cardinalità è fissa.
Occorre ottimizzare le interrogazioni che sono
frequenti: il modello tabella ordinata con
algoritmo di ricerca binaria non utilizza la frequenza
di accesso; “albero” e’ un albero binario
implementato con una struttura tabellare statica (non
di tipo dinamico).
74
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Lunghezza media dell’ albero P strumento usato
per poter scegliere in base alle frequenze d’ accesso
la forma dell’ albero che minimizza P (ricordarne le
espressioni: lucidi 7 e seg.).
Costruzione dell’ albero ottimo la cui forma produca il
minimo costo di ricerca fra tutti gli alberi binari di ricerca
contenenti le stesse chiavi.
IPOTESI
Le n chiavi da porre nell’ albero sono tutte presenti,
ordinate in senso crescente e contrassegnate da indici
numerati da 1 a n (k1,k2,… kn con k1=array, k2=begin
…in Pascal o k1 =auto, k2=break … in C);
Sono note le probabilita’ che risulti x = ki ossia
Pr{ x= ki } = pi per i =1, 2,…n e con x=argomento
di ricerca;
Sono note le probabilita’ che risulti x ki ossia
Pr{ki < x < ki+1 } = qi per i =1, 2,…n-1 ed inoltre
Pr{ x < k1} = q0;
Pr{ x > kn} = qn con il vincolo
che:
n (pi) + n (qj) =1.
Si definisce costo dell’ albero
la sua lunghezza media pesata con le probabilita’ pi di
accesso ai nodi normali e qi di accesso ai nodi esterni ossia:
i=1
j=0
Pmedia = pihi + qjhj’ = Pi media + Pe media
i=1
j=0
dove hi e hj’ sono le lunghezze dei
nodi normali ed esterni date dai livelli, (cfr. espr. pag.8).
n
n
In pratica invece delle probabilita’ si usano contatori
di frequenza (ai per pi e bj per qj) arrivando all’
espressione della lunghezza cumulata pesata data da:
75
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
P = aihi + bjhj’
i=1
j=0
e quindi Pmedia = P/W con il peso dell’
n
n
n
n
albero definito da W = ai + bj
i=1
j=0
Esempi del Criterio di Scelta della forma con la
lunghezza di ricerca cumulata:
a3 =6
Albero ottimale di 3 nodi normali e 4
esterni con Key1=3, Key2=5, Key3=9;
a1=1, a2 =2, a3 =6; b0=b1=b2=b3=1;
Ci sono 5 forme ammissibili: una
key <3
La sua
9
9 < key
3
5
3< key <5
P= i ai hi + i bi h’i=6+2+6+
+2+3+4+4=27
5<key<9
Un’ altra forma e la relativa P seguono:
P= i ai hi + i bi h’i=2+2+12+3+3+3+3=28
5
3
key <3
9
3<key <5
9<key
5<key <9
La terza forma e la relativa
P sono:
P= i ai hi + i bi h’i=6+4+3+2+3+4+4=26
9
9<key
L’albero ottimo e’ in questo caso
la lista lineare !
L’albero ottimo di 3 nodi
key <3
normali e 4 nodi esterni e’
indicato con T03
5
5< key <9
3
3<key <5
76
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’albero ottimo di 4 nodi normali
e 5 nodi esterni e’ T03 + nuovo nodo normale in
posizione ottimale !
Da quest’ ultima considerazione si puo’ partire per
qualche cenno sull’ algoritmo di costruzione di T0n
che:
si basa sulla proprieta’ fondamentale degli alberi
ottimi che dice: “Tutti i sottoalberi di un albero
ottimo sono ottimi” (pag. 228-229 Wirth fornite
nel luc. 71) ossia
P = Pleft + W + Pright
e quindi se P e’ ottima lo sono pure Pleft e Pright
si basa sul formalismo proprio della struttura
che indica in Ti,j l’ albero ottimo formato da j-i
nodi normali (con le chiavi ki+1, ki+2,… ki+j e
contatori di frequenza ai+1, ai+2, … ai+j) e da ji+1 nodi esterni (con contatori di frequenza bi,
bi+1, bi+2, … bi+j (Si noti come questo
formalismo a 2 indici introduca la forma
matriciale per implementare rispettivamente i
parametri peso Wi,j e lunghezza Pi,j dell’ albero
Ti,j.)
L’ algoritmo inizia col costruire gli alberi Ti,i di
0 nodi normali ed 1 nodo esterno;
Poi quelli Ti,i+1 di 1 nodo normale e 2 nodi
esterni;
77
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Poi quelli Ti,j = Ti,i+2 di 2 nodi normali e 3 nodi
esterni scegliendo quello con la forma che
produce la minima Pi,j = Pleft + Wi,j + Pright …
aggiungendo un nodo normale alla volta viene
costruito l’ albero ottimo T0,n di n nodi normali.
Ma la complessita’ ? Dovendo cercare
l’elemento ottimo di una matrice (n*n) da
scandire riga per riga sembrerebbe O(n3)…
Invece analizzando e sfruttando “al meglio” le
proprieta’ degli alberi ottimi si arriva a
Complessita’ O(n2).
Per più dettagli: Wirth pag.230-240 col programma
optimal_tree dove il numero di parole riservate (di
un linguaggio Pascal-like) =31: in generale se ne
avranno al piu’ 100 dimensione corretta di un
Albero Ottimo ... e di un albero binario in generale!
78
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
79
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
2a Sez.
Interrogazione di archivi:
problemi e soluzioni specifiche con
Strutture Multidimensionali: k-d tree,
Quad-tree, R-tree e loro utilizzo
problemi e soluzioni tradizionali in ambiente
multiutenza con archivi indicizzati &
Sistema di Indici
80
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Interrogazione di archivi:
_ chiave primaria (e alternative);
_ chiavi secondarie.
Problema organizzazione degli archivi
si articola in sottoproblemi:
_ velocita’ di risposta &
_ precisione di risposta anche con attivita’ di accessi
simultanei per ogni tipo di interrogazione.
Soluzioni possibili:
1. Soluzioni di tipo specifico alberi a piu’ dimensioni
considerazioni successive con pag. di es. da articoli,
2. di tipo tradizionale archivi indicizzati (file
indexati): applicazioni del Modello teorico di file
indexato di Wirth (lucido 60) e Sistema di Indici, con
pag. di esempio da dispense: +oltre
81
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
1. Soluzioni di tipo specifico: alberi a piu’ dimensioni
Problema: estrazioni di dati soddisfacenti condizioni su
un numero prestabilito di attributi (= chiavi secondarie).
Soluzione: strutture multidimensionali cosi’ chiamate
perche’ ogni record puo’ essere interpretato come un
punto nello spazio a k-dimensioni essendo k il numero
delle chiavi secondarie che lo identificano.
I record sono quelli di un archivio in cui ogni record
contiene k chiavi a1, a2, … ak ordinate ed altri campi
(trascurati per sinteticita’). Ogni interrogazione puo’
essere:
specificata esattamente: a1 = x, a2 = y, … ak = z
con risultato = 1 record (o anche 0 record) con
possibilita’ di inferenza statistica da un’
interrogazione apparentemente innocua si
possono estrarre informazioni riservate come per
es. la targa dell’ automobile di un utente
privilegiato (polizia, servizi segreti …)
specificata parzialmente: a1 = x, a2 = r, e
nessuna condizione sulle altre chiavi con
risultato = un insieme di record (o anche 0)
specificata su un intervallo: x1 a1 x2 … z1
ak z2 con risultato = un insieme di record (o
anche 0 record)
specificata su un intervallo parzialmente
specificato (solo sulle prime r chiavi con r < k)
con risultato = un insieme di record (o anche 0
record)
Finora tutte queste interrogazioni sono di tipo
intersezione.
82
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Ci sono poi le interrogazioni
di cardinalita’ con risultato = # di record
di vicinanza con risultato = 0, 1, +record
vicini ad un record specificato
Si noti: il concetto di vicinanza implica aver
definito una metrica … (Where wheat is grown ?
Spatial indexing !!)
Dovendo stabilire una metrica sui dati da
rappresentare, questi vengono indicati come “dati
spaziali” ed in Atzeni & … sono introdotti molto
brevemente
nel
capitolo
dedicato
alle
O.O.D.B.M.S. definendoli nel contesto dei Sistemi
Informativi Geografici…(ma la Geografia e’
intesa in senso lato ossia puo’ “spaziare” in svariati
campi, non solo relativi alla superficie terrestre e
non solo a 2 dimensioni !!) Nella Grafica ci sono le
applicazioni più interessanti, per es. del tipo trovare
tutte le immagini che contengono una data
caratteristica e/o tutti i punti collegati da un
percorso=strada …ma esistono tante altre possibili
applicazioni e aspetti.
Nel testo “Principles of Data Mining” di Hand,
Mannila, Smyth, 2001 The MIT Press, sono
introdotti i modelli ad albero nel contesto della
classificazione dei dati per la previsione di
variabili: tra le k chiavi e’ scelto un discriminante,
di cui si parla nel seguito, in modo da ottimizzare
una funzione obiettivo.
83
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
(Per esempio nel campo diagnostico tale funzione
puo’ essere lo scarto quadratico medio tra i valori
dati e quelli attesi o un test statistico: in generale si
tratta di una funzione statistica dei dati.)
Cosa si intende per Data Mining e’ gia' stato
indicato in d.b.2005p2. ( = Processo di esplorazione teso a scoprire
interrelazioni (anche le – evidenti) tra dati della stessa natura, ma di varia
Ricordando gli
esempi di problemi classici risolti dal Data Mining
usando regole di probabili associazioni, sembra
corretto integrare quanto detto relativamente alle
regole di associazioni basate su A.I. (Artificial
Intelligence). Come già indicato, queste sono
“dedotte” dalle tuple delle relation presenti prese in
esame per evidenziare i probabili elementi di una
regola associativa contenuti in esse“tra le righe!”
provenienza per indagare le loro analogie o differenze.
(Un loro tipico esempio era: sci bastoncini).
Un approccio analogo è seguito anche nel Datalog
che è un linguaggio di interrogazione di Basi di
Dati
basato
sul
ProLog
(acronimo
di
Programmation Logique). ProLog permette di
specificare un problema espresso con enunciati
logici (predicati) in formalismi logici. Un problema
viene posto in forma di verità (predicati
dichiarativi) da dimostrare da parte del motore
inferenziale (alla base di ProLog) con
l’applicazione delle regole di inferenza ai fatti
enunciati (dati).
84
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Esempio: date le 2 regole
nonno(x,z) IF padre(x,y), padre(y,z)
nonno(x,z) IF padre(x,y), madre(y,z)
ed i fatti seguenti:
padre(Enzo,Pino);
padre(Andrea, Sara);
madre(Sara,Lea);
madre(Livia, Enzo);
bionda(Lea); ….
… (prima di pensare alle possibili interrogazioni,
una riflessione. I fatti sopra considerati non
assomigliano alla relation Genitori di un d.b. ?)
le interrogazioni da dimostrare possono essere:
?bionda(x),nonno(Andrea,x)
?nonno(x,y,bionda(y))
Il motore inferenziale prende in esame i fatti,
applica le regole di inferenza, trasforma i fatti in
altri fatti finchè tra questi trova la tesi.
Uguale comportamento si ha per il Datalog: una
semplice interrogazione del tipo ‘trova tutti i
fornitori in London’ in Datalog è formulata con:
?Fornitore(S# : s, Sname : n, Status : t, City : London)
(ossia trova tutti gli s di S#, gli n di Sname, i t di Status dove
ed ha in risposta la
‘selection on City =London’ della tabella Fornitore.
City=London),
85
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Un’ altra interrogazione del tipo ‘trova tutte le parti
fornite in quantità < 9’ ha in risposta la vista
PocheParti e viene formulata con una regola
associativa del tipo seguente:
PocheParti (P# : p, Pname : n) Parte(P# : m , Pname : e,
Colore : c, Peso : w), Parte_fornita(P# : m, S# : s , Qty : q), q<9
Si noti come il Join tra Parte e Parte_fornita è
indicato dalla variabile m comune alle 2 relation.
Si noti anche che l’ ultima regola associativa segue la
forma: testa corpo
La testa della regola associativa è un predicato
intensionale (per es. una vista o una virtual relation)
ed il corpo della regola è una lista di condizioni
sulle relation del d.b. costruita nello stile del calcolo
dei predicati.
Tornando al problema delle chiavi secondarie, esiste
una classe di strutture dati di tipo gerarchico, basate
sul principio della decomposizione ricorsiva dei
dati che comprende strutture multidimensionali per
estrarre quei dati soddisfacenti le interrogazioni
indicate ossia di tipo intersezione, di cardinalita’ e
di vicinanza: i k-d alberi (k-d tree), i 2d -tree e gli
R-tree appartengono a questa classe.
Il k-d tree (struttura k-dimensionale) e’ un’
estensione dell’ albero binario di ricerca nello
spazio delle k chiavi secondarie: puo’ risiedere in
C.M. o su disco in dipendenza dal valore di k.
86
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ analogia con l’ albero binario di ricerca e’ che si
sceglie una chiave (tra le k) come discriminante; la
differenza e’ che la scelta cambia ad ogni livello
dell’ albero.
Per la radice si usa a1;
a livello 2 si usa a2; …
a livello k si usa ak;
esaurite tutte le k chiavi si torna a considerare la
prima:
a livello k+1 si usa di nuovo a1;
a livello k+2 si usa di nuovo a2 e cosi’ via.
Ogni confronto produce 2 insiemi dall’ insieme di
partenza 2 sottoalberi
Record con chiave ai sottoalbero sinistro
“
“ “
> ai sottoalbero destro
difficile il bilanciamento !!
La suddivisione prosegue finchè il sottinsieme
ottenuto può stare in una pagina del k-d albero.
Se il k-d albero risiede in C.M. la rappresentazione
delle pagine e’ omogenea. In C.M. ogni pagina
contiene un record completo, l’ indice della chiave
discriminante i 2 puntatori sinistro e destro. Se il
k-d albero risiede su disco la struttura delle sue
pagine puo’ assumere 2 formati diversi
(analogamente a quella dei b*tree). In questo caso
nelle pagine non foglie, radice compresa, si trova
solo la chiave discriminante, il suo indice e i 2
puntatori sinistro e destro, nelle foglie i record completi.
87
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Nel contesto del Data Mining,
per la
classificazione e previsione di variabili dipendenti
dai dati, la funzione obiettivo deve migliorare ad
ogni confronto (passo di suddivisione); se peggiora
o l’ insieme non si suddivide … o si esclude il
sottoinsieme che produce il peggioramento.
Nell’ Esempio successivo se lo scopo della ricerca
è scegliere un nuovo modello di automobile simile
alle macchine anni ’70-’80 (Giulietta, Maggiolino,
…), si definirà una funzione obiettivo data dalla
differenza tra le caratteristiche del nuovo modello e
quelle dei modelli degli anni ’70-’80 e per ogni k
chiave si valuterà quale sottoinsieme ottimizza la
funzione obiettivo.
Il problema del bilanciamento si puo’ tentare di
risolvere:
individuando quei discriminanti che permettono
una ripartizione bilanciata delle chiavi, ma … non
e’ facile; oppure con un altro tipo di struttura: il 2dtree (dove d e’ la dimensione
se d=2 si ha il quad-tree
se d =3 si ha l’ oct-tree
…
)
e la sua “linearizzazione” che permette di
implementarla come b*tree.
Prima di introdurre i 2d-tree si considera il k-d tree
costruito per l’ esempio relativo alle automobili.
88
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Suddivisione di Spazio a k dim. in k insiemi=iperrettangoli
Esempio: Automobili costruite dopo il 1983 con
DISCRIMINANTE 1 = colore,
DISCRIMINANTE 2 = MARCA,
DISCRIMINANTE 3 = modello (Base, Diesel,
Wagon …)
(Si considera questo sottoinsieme per escluderlo
subito.)
MARCA
modello
VW
TALBOT
RENAULT
PORSCHE
IBIZA
FIAT
ALFA
azzurro bianco blu GIALLO grigio nero rosso verde colore
L’ Esempio si riferisce alla situazione mostrata nel
lucido successivo; un altro esempio nel lucido
ancora successivo.
89
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
90
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
91
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Quad-tree & Oct-tree (Finkel & Bentley 1974)
Paradigma di base: divide et impera;
Definizione di 2d tree il numero d di
dimensioni diventa esponente di 2 anche a
significare che le dimensioni in questo modello
sono usate simultaneamente ...
Nel seguito si considerano principalmente i Quadtree e precisamente i Region-Quad-tree anche se il
prefisso Region e’ spesso omesso. Il motivo della
sua introduzione e’ che esistono 2 tipi di Quad-tree:
i Point-Quad-tree ed i Region-Quad-tree.
La distinzione tra i Region-Quad-tree ed i PointQuad-tree e’ di Hanan Samet in “The Design
Analysis of Spatial Data Structure”, Addison
Wesley, 1989. Samet definisce Region-Quad-tree
quella struttura in cui “le regioni risultanti dal
processo di suddivisione hanno uguali dimensioni”
cosa che non avviene per i Point-Quad-tree. Per
questi (come per i k-d tree che talvolta ne possono
rappresentare un miglioramento) i punti che
individuano i dati diventano i punti di suddivisione,
dando luogo a regioni di dimensioni diverse.
Esistono vari metodi per adattare i Region-Quadtree a rappresentare i Point-Quad-tree: un modello
usato per associare i punti dati alle regioni
(quadranti) di suddivisione e’il PR Quad-tree dove
P indica Point ed R Region ed e’ sostanzialmente
quello descritto nel seguito.
92
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Quad-tree & Oct-tree Si considera un insieme S
di n punti in uno spazio d-dimensionale: S = {P1,
P2,… Pn} essendo ogni punto Pi = (pi1,pi2,…pid)
espresso da una d-upla di coordinate.
Un 2d tree per S si ottiene considerando un punto Pi
di S come radice dell’ albero e confrontandolo con
un qualsiasi altro punto Pj di S: si ottengono 2d
possibili alternative. Quindi Pi divide S in 2d
sottoinsiemi che diventano i figli di Pi nell’ albero
(vedere disegni e appunti nel lucido seguente). Il
procedimento e’ iterato ricorsivamente per ogni
sottoinsieme (nodo dell’ albero) con piu’ di un
punto.
Nel piano (S bidimensionale) un quad-tree e’ un 22
tree in cui ogni nodo o e’ foglia o ha 4 figli che
rappresentano i 4 quadranti in cui viene suddiviso il
piano da un suo punto. Il piano e’ visto come un
quadrato universale che corrisponde al nodo
radice dell’ albero: la suddivisione e’ iterata
ricorsivamente fino a incastonare tutti i punti in
quadranti sempre piu’ piccoli. Tali quadranti, per i
quali non sono necessarie ulteriori suddivisioni,
corrispondono alle foglie dell’ albero. Si noti che
nei 2-d tree per discriminare i punti del piano prima
si usava una retta parallela all’ asse Y, poi una
parallela all’ asse X e cosi’ via; nei 22 tree le rette
(virtuali) funzionano simultaneamente.
93
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Nello spazio 3-D un oct-tree si ottiene
considerando che un punto P suddivide lo spazio
(cubo universale) in 8 parti (cubetti) che
diventano i suoi figli in un 23 tree ossia in un
albero di grado 8. Esempi & algoritmo di
costruzione di un quad-tree in Algol da Acta
Informatica nei lucidi ancora successivi. Loro
maggior uso: GRAFICA !!
94
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
95
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
96
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Linearizzazione dei Quad-tree
L’ idea di base e’ passare da una struttura a d
dimensioni, come e’ l’ albero 2d, ad una struttura
lineare che lasci consecutivi tutti i punti
appartenenti allo stesso insieme (“quadrato”) ddimensionale.
Per la linearizzazione esistono varie possibilita’ con
uso di codici diversi e che producono varianti del
modello linearizzato.
Una possibilita’ per i quad-alberi e’ usare la
Chiave di Peano dedotta dalla Curva di Peano: un
frattale che passa per tutti i punti del piano e
mantiene la sua struttura e complessita’ ad ogni
livello di scala.
Il metodo e’ stato introdotto da R. Laurini (Univ.
Lione) e indipendentemente da Dalla Libera,
Gosen, Quartieri (Univ. PD) negli anni 1980-90.
Sinteticamente:
_ ad ogni punto del piano corrisponde un valore
della curva di Peano: si assume come chiave del
punto;
_ l’ ordinamento della chiave lascia consecutivi i
punti appartenenti ad uno stesso quadrato del quadalbero a qualsiasi livello di suddivisione.
97
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Deduzione logica:
Ottenuta la linearizzazione il quad-tree puo’ essere
“visto” come un archivio inverso (cfr. +avanti, ma
in sintesi interpretabile come un indice) ed
implementato con un b*tree (o un b+tree) ordinato
sulla Chiave di Peano risolvendo i problemi di
bilanciamento.
Per la Curva e chiave di Peano cfr. appunti nel
lucido successivo dal “Formulario matematico”
1908 in “Opere Scelte” , Vol. 1 a cura di U.M.I. e
C.N.R., ed. Cremonese, Roma 1957.
98
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
N
Segue Chiave di Peano a
da Laurini (Univ. Lione, Atti del
Congresso EUROGRAPHICS’85)
99
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
100
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Per costruire la chiave di Peano a N (in cui il generatore
appare come una N -appunti nel lucido precedente tratti da Laurini
‘85-) da una coppia di coordinate intere X e Y (quali sono
quelle di uno schermo) basta “interallacciare” le r+1
cifre (i bit) di X,Y ottenendo da:
X = xr, xr-1, … x1, x0
Y = yr, yr-1, … y1, y0
KeyPeano = (2xi + yi) 4 i Regola di composizione!
r
i=0
Notare:
con 1 bit per X e Y la Key = (00,01,10,11) ossia è di 2 bit e individua 4 punti;
1
2
con 2 bit per X e Y la Key = (0000,0001,0010,…1111) è di 4 bit e individua
2
16 punti ossia 2
2
4;
con r bit per X e Y la Keyr ha un numero di bit pari a 2 elevato alla r
ed individua un numero di punti = 2r.
Se per esempio X e Y sono espressi con 2 bit con:
X= 0110 (0 in posizione 1 ed 1 in posizione 0)
Y= 1110 (1 “ “
“ “ 1 “ “
“)
si
ottiene:
KeyPeano = 1 (2xi + yi) 4 i = ((2+1) 40 +(1) 41))10 =(10+1+100)2 =
i=0
=0 1 1 12=710
con il primo 0 in posizione 3 (da X), il primo 1in posizione
2 (da Y), il secondo 1 in posiz. 1 (da X), il terzo 1 in posiz.
0 da (da Y). Risulta:
KeyPeano= (y0+2x0) 4 0 + (y1+2x1) 41 =
= (y0+2x0) 2 0 + (y1+2x1) 2 2
101
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Quindi con X,Y espressi in base 2 con r bit e tali che:
0 X 2 r –1; 0 Y 2 r –1; si ha: 0 KeyPeano 4 r–1= 2 2r –1
che fornisce la chiave corrispondente alla “curva
ricorsiva” di Peano a N. (Si noti nell’ es. del luc. precedente:
0 X, Y 22-1; 0 KeyPeano 24 -1) .
Si nota che il numero di bit necessari per la
rappresentazione di KeyPeano e’ doppio di quello
necessario per X o Y. Quindi (almeno fin qui) non
c’e’ risparmio di memoria, ma allora perche’
linearizzare ? In generale: individuare i punti di un
insieme (archivio) con un codice unico permette di
effettuare un’ inversione sull’ archivio costruendo un
indice da implementare con un b*tree. Inoltre l’
obiettivo della linearizzazione non era risparmiare
memoria, ma riuscire a implementare un quad-albero
come un b*-tree o una struttura simile ordinata su un
codice (Chiave di Peano) risolvendo i problemi di
bilanciamento; se poi si riesce anche a risparmiare
memoria … meglio !! Seguono alcuni esempi di
procedimenti.
Si pensi per semplicita’ all’ archivio dei punti del
piano +tipicamente usato in informatica il video
display composto da alcuni pixel, per es. da
1024*1024 PIXEL. Individuare i pixel con un codice
univoco da’ la possibilita’ di effettuare un’ inversione
su tale archivio costruendo un indice sui pixel.
102
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Nel contesto del d.b. si puo’ considerare una relation
definita per ogni pixel di cui si vuole evidenziare il
colore il cui schema e’ il seguente:
Griglia (X,Y, colore).
L’ indice su X,Y si puo’ esprimere con:
Ind_gri (X,Y, code)
dove code e’ il codice univoco che individua i punti di
coordinate X,Y. Si noti che si possono costruire
diversi codici, usando anche altre curve che passano
per tutti i punti del piano come quella di Hilbert, ma
quello +semplice e ottimale e’ la chiave di Peano a N.
L’ indice spaziale Ind_gri permette:
di indirizzare i pixel del video display usando per
esempio Griglia1(code,colore) che sostituisce
Griglia
e di individuare i punti di un’ immagine del piano.
Si noti per prima cosa che si ottiene un
ordinamento dei punti del piano che non e’ l’
ordine “lexicografico” (usato per es. in topografia)
che ordina i punti del piano P(X,Y) prima sui valori
di X e poi su quelli di Y, ma e’ stato dimostrato che
la distanza media tra punti nell’ ordinamento “di
Peano” e’ minore di quella calcolata con l’
ordinamento lexicografico … +accuratezza !
Il problema di individuare i punti di un’ immagine
rientra nella classe dei “problemi geografici” del tipo
seguente
103
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
“Problemi geografici” Determinare i punti del
piano cartesiano appartenenti ad un dato poligono.
(Il poligono puo’ individuare una zona petrolifera,
l’insieme dei ricoverati in via di guarigione, …) La
soluzione di questo tipo di problemi si ottiene
confrontando i punti del piano con quelli appartenenti
al poligono. Questi si possono individuare con un
Quad-tree contenente il poligono e posizionato con il
vertice piu’ in basso a sinistra nell’ origine del piano. I
quadrati del quadtree - ottenuti per suddivisioni
ricorsive di un array iniziale di 2r*2r elementi (pixel)
in regioni (quadrati) del piano sempre piu’ piccole
fino al pixel - si possono individuare usando la
chiave di Peano a N. Il Quad-tree e’ allora detto
Peano-based.
In un quadtree Peano-based ogni quadrato e’
localizzato tramite la chiave di Peano a N che
compete al suo vertice in basso a sinistra. L’
ordinamento ricorsivo permette teoricamente la
fusione dei quadrati del quadtree dai piu’ piccoli
(pixel) ai piu’ grandi fino all’ intera griglia che li
contiene tutti. Per convincersene basta ragionare
sulla figura 2b della fotocopia tratta da Laurini ‘85
(fornita nel lucido seg.). Appare che la KeyPeano (a
N) relativa all' origine del piano cartesiano puo’
individuare sia il quadratino di un pixel, sia quello
di 4 pixel, sia l’ intera griglia… basta aumentare il
numero delle cifre componenti la chiave di Peano stessa.
104
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Perché P 26? Si ha: 0 x,y 7= 23-1 (con 3 bit si rappresentano valori fino a 7). La P necessita del doppio di bit
105
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
La codifica della KeyPeano dei primi 4 pixel (visti
come 4 quadratini di lato 1), richiede 1 cifra in base
4 (ossia 04, 14, 24, 34, ossia 2 bit): insieme essi
forniscono un quadratino di lato 2 individuato dalla
KeyPeano=0.
I primi 4 quadratini di lato 2 sono individuati
ciascuno dalle KeyPeano 010, 410, 810, 1210 che sono
multiple di 4 e richiedono 2 cifre in base 4 (04, 104,
204, 304) ossia 4 bit …
La codifica della KeyPeano di tutta l’ array
richiede r cifre in base 4 ossia 2r bit.
Questo ordinamento ricorsivo dei quadrati uno
interno all’ altro e tutti contenuti nell’ array iniziale,
permette la fusione dei quadrati dai +piccoli ai
+grandi purche’ le KeyPeano che li identificano
siano multiple di 4.
Esempi di utilizzo di tale ordinamento ricorsivo
1. la ricostruzione di un’ immagine di colore per
es. nero su fondo bianco (algoritmo elementare
qui sotto schematizzato);
2. trovare i punti interni ad un poligono contenuto
nell’ array iniziale (algoritmo di Dalla Libera,
Gosen, Quartieri, Atti Aica 1982);
_…
L’ algoritmo relativo al primo problema scandisce
l’ array iniziale 2 r*2 r contenente l’ immagine
incastonata in un Quad-tree (vedere fotocopia
Laurini ’85 Fig.3a-c), pixel per pixel.
106
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Sono considerati per primi i pixel a partire da quello
con KeyPeano=0.
Quando l’ algoritmo trova 4 pixel consecutivi dello
stesso colore, se il primo ha KeyPeano multipla di 41
o 0 li fonde in un unico quadratino di lato 2 che
viene inserito (sostituendoli) nella relation che in
figura 3d della fotoc. Laurini ’85 rappresenta il
quadtree, ossia:
Quad(KeyPeano, nomequadratino,latoquadratino,colorquadratino)
Se invece i pixel sono di colore diverso vengono
inseriti tutti singolarmente nella relation Quad.
La fusione utile anche a risparmiare memoria si
ripete per i quadratini di lato 2 a partire da quello
con KeyPeano=0. Quando l’ algoritmo trova 4
quadratini di lato 2 consecutivi dello stesso colore,
ed il primo con KeyPeano multipla di 42 o 0, li fonde
in un unico quadratino di lato doppio (ossia di lato
4) che viene inserito (in loro sostituzione) nella
relation Quad.
In generale la fusione e’ applicata ai quadrati
(inclusi nell’ array) di lato i, per ogni i 2r-1,
purche’ le KeyPeano che li identificano siano
multiple di 4i se i quadrati sono dello stesso
colore, sono fusi in un quadrato di lato 2i che viene
inserito (in loro sostituzione) nella relation Quad.
Pero’ e di nuovo per ogni i < 2 r, (e positivo) se i
quadrati sono di colore diverso vengono inseriti
tutti singolarmente nella relation Quad.
107
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
La relation Quad che rappresenta il quad-albero
e’ ordinata sulla KeyPeano e potra’ essere
implementata come un B*tree o altra struttura
bilanciata.
Relativamente al problema 2 ossia
trovare i punti interni ad un poligono contenuto
nell’ array iniziale,
un algoritmo risolutivo può essere inserito nel
programma che elabora i punti del piano nel modo
seguente.
In input viene fornita la coordinata Max dei punti
del piano che si vogliono considerare ed il loro
numero MN, ed anche il numero di vertici N del
poligono detto poligono di query;
per ciascuno degli MN punti:
sono calcolate le coordinate (x,y) (per es. in una
simulazione tramite un generatore pseudocasuale) nell’ intervallo 0 – Max,
viene costruita Key = Peano (y,x),
e la Key viene inserita in un b*tree;
Viene costruito il poligono di query di N vertici
tramite la procedura crea_polig(N) che, lette le
coordinate di un vertice, controlla che il vertice sia
interno al quadrato universale di lato Max (se in un
caso reale lo superasse occorrerebbe aggiornare
Max o il vertice), e che il poligono in costruzione
risulti convesso.
108
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Per l’ interrogazione:
viene costruito il quadrato limite che contiene al
suo interno il poligono di query (senza sprechi)
e dal suo lato è dedotto l’ esponente Z di 2 che
lo maggiora al minimo. Si possono verificare 4
casi di cui più interessante è il primo ossia:
(xx,yy)
In questa situazione in cui risulta il lato=2Z verrà
attivata una procedura ricorsiva di ricerca dei punti
appartenenti al poligono iniziando dai 4
sottoquadrati di lato=2Z-1, con attivazioni del tipo:
search(xx,yy,Z-1)
search(xx,yy+2Z-1,Z-1)
search(xx+2Z-1,yy,Z-1)
search(xx+2Z-1,yy+2Z-1,Z-1)
La search visita i nodi del quad-tree scartando quelli
che non contengono punti interni al poligono di
query; in caso contrario, in ogni nodo scende nel
quad-tree con con altre 4 attivazioni della procedura
search dove l’ esponente diventa Z-2 ed i punti
iniziali cambiano opportunamente. La procedura
search opera in questo modo ricorsivamente a meno
che il numero atteso di punti sia abbastanza basso da
permettere una loro scansione sequenziale (come nel caso considerato
avverrà per il sottoquadrato individuato da search(xx,yy,Z-2) .
109
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ ultima struttura gerarchica presentata di seguito è
l’ albero R che viene utilizzato per implementare
indici spaziali in Oracle. Nella guida di Oracle è
indicata l’ applicazione Spatial Index Advisor che
“facilita l’ analisi e la regolazione degli indici
spaziali Oracle da parte degli amministratori al
fine di ottenere buone prestazioni per le query
spaziali … su dati che rappresentano oggetti quali
rettangoli, cerchi, poligoni e archi…”
Ai dati spaziali può essere associato un indice
spaziale che contiene una ‘copertura’ della zona
interessata fatta da ‘tasselli’. Le nozioni ed i dettagli
sulle
tecniche
fondamentali
relative
all’
implementazione realizzata in Oracle sono nel
manuale “Oracle Spatial User’s guide and
reference”, ma la pagina Spaziale delle proprietà
indice presenta le possibili strutture utilizzabili per
creare un indice spaziale. Tali strutture nelle
versioni 8i ed anche 9i sono: R-tree e Quad-tree.
Inoltre la struttura R-tree è la preferita perchè
sembra consentire prestazioni migliori con un
lavoro semplificato per la sua creazione e
amministrazione.
R-tree: si tratta di una struttura gerarchica derivata
dal B+tree che viene usata (con modelli derivati
detti R+ tree o R*tree) per creare indici “spaziali”
in vari DBMS (come in Oracle8i-9i dove sono usati per
default
su
colonne
di
dati
spaziali).
110
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Scopo degli R-tree e’ rappresentare dati ossia oggetti jdimensionali che si ipotizzano racchiusi in rettangoli (a j
dimensioni. Valgono “regole” simili a quelle dei B+tree
con k (ordine) = #min. e 2*k=#max. termini e figli nei
nodi non radice dove puo’ stare anche solo un termine.
Ogni nodo non foglia di un R-tree corrisponde al piu’
piccolo rettangolo j-dimensionale che contiene i suoi figli;
il suo termine generico e’ una coppia data da (R, P) dove R
e’ un rettangolo (j-dimensionale) contenitore di altri rettangoli
che si assegnano al suo nodo figlio puntato da P.
Tutti i nodi foglia di un R-tree sono allo stesso livello ed
ogni nodo foglia contiene m coppie delle forma (R,O) dove
R e’ il piu’ piccolo rettangolo j-dimensionale che
spazialmente contiene l’ oggetto O con k m 2*k
(k=ordine albero)…
Piu’ in generale O può essere un puntatore ad oggetti
(tabelle) di un d.b.
Es. per semplicita’nel piano: insieme di oggetti = rettangoli a 2-dimensioni
(0,40)
R1
R3
7
A
R2
I
R5
B
J
Z
I
C
R6
F
E
(0,0)
R4
T
(40,40)
Oggetti a 2-dim. sono
i rettangoli A, B, C,
E, F, I, J, T, Z.
I rettangoli box
(contenitori) hanno
perimetri tratteggiati.
7 e’ il nome di un box
di cui si parla +oltre
Rombo = una finestra di query
(40,0) FIG.1
Il corrispondente R-tree di ordine k=2 appare in FIG.2:
111
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
R1 R2
R3 R4
A I
R5 R6
E T
B C
Z F J
FIG.2
Si noti: qui gli oggetti O sintetizzano oggetti e
rettangoli contenitori. Inoltre R-tree non e’ unico:
per es. l’ oggetto J potrebbe essere contenuto anche
in R1.
La struttura di R-tree dipende pesantemente dall’
ordine in cui gli oggetti dell’ insieme ed i box che
li contengono sono inseriti in (ed eventualmente
cancellati da) R-tree. Come i B+tree gli R-tree
crescono dalle foglie ed e’ anche previsto un
algoritmo di split se i termini inseriti in un nodo
superano 2*k.
Nel valutare la lunghezza di ricerca di un R-tree e’
importante considerare i concetti di copertura e di
overlap = sovrapposizione.
La copertura di un livello di un R-tree e’definita
come l’ area totale di tutti i box relativi ai nodi di
quel livello. L’ overlap e’ definito come l’area
totale contenuta in piu’ nodi.
112
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ efficienza della ricerca richiede che entrambi
copertura ed overlap siano minimi.
Copertura minima riduce la quantita’ di spazio
“morto” coperto dai nodi. L’ overlap e’ anche piu’
importante
Si consideri una finestra di ricerca o
“rettangolo” di query, (nel caso della FIG.1 e’ il
rombo ), che si trovi in un’ area comprendente n
box ossia nodi di R-tree a livello x;
nel caso peggiore occorre eseguire n cammini alle
foglie ossia uno per ogni nodo che si sovrappone
con (h-x+1)*n accessi ai nodi invece di (h-x+1). (In
FIG.1 il rombo e’ dentro il box R1 e R3 ed anche
fa parte di R2 ed R6: quindi deve essere eseguita
una ricerca sia nel sotto-R-tree con padre R1, sia in
quello con padre R2 e solo questo restituira’ i
punti dell’ oggetto J che è tutto contenuto in R2, e
solo parzialmente in R3.) Senza un appropriato
controllo dell’ overlap (per es. in operazioni di
insert) la lunghezza di ricerca puo’ degenerare da
logaritmica a lineare.
Il controllo dell’ overlap non e’ semplice
specialmente durante lo split dinamico dei nodi
nelle inserzioni.
Per superare l’ ostacolo e’ stato introdotto una
variante del modello ossia gli R+tree, come
riportato da Sellis, Roussopoulos, Faloustos dell’
Universita’ del Maryland (1988).
113
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ idea alla base degli R+tree e’ permettere che un
oggetto (nell’ esempio di FIG.1 un rettangolo che lo
rappresenta) possa appartenere a 2 o piu’ box
contenitori che non devono sovrapporsi. Negli
R+tree i box contenitori devono raggrupparsi in
modo da non sovrapporsi. (In FIG.1 i box R3 ed
R2 devono essere ridotti di una parte in modo da
non sovrapporsi: in R1 é introdotto un nuovo box
7 che può contenere il rettangolo I per circa 1/3,
mentre gli altri 2/3 di I restano nel box R3. Il
corrispondente R+tree appare nel lucido seguente
FIG.3).
Si noti che evitare l’ overlap produce un aumento di
termini nei nodi di R+tree che puo’ portare ad un
incremento dell’ altezza: si tratta pero’ di un
incremento logaritmico distribuito su tutto l’
albero. Inoltre l’ incremento dell’ altezza e’
compensato dal beneficio di evitare molteplici
cammini di ricerca usando finestre di query. (Nell’
esempio di FIG.1 per individuare il rettangolo I
avendo gia’ effettuato una ricerca dal padre R1 e
figlio R3-ridotto fino alla foglia con I2/3, bastera’
una ricerca in piu’ nel sotto-R+tree
con
“radice” (R3-ridotto, R4 e 7) fino alla foglia con
I1/3. Si noti ancora che in 7 e’ anche contenuta
tutta la finestra di query e tutto l’ oggetto J.)
Segue la FIG.3
114
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
R1 (R2 -7)
(R3-7) R4 7
A I2/3
ET
R5 R6
I1/3 J
B C
D F
FIG.3
Specifiche +approfondite sugli R+tree e relativi
algoritmi sono lasciati all’ interesse degli studenti.
115
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Nelle considerazioni fatte finora non si è trattato il
problema degli accessi concorrenti, nel senso che l’ accento
si è posto su nuove strutture che danno luogo ad archivi ed
indici da interrogare … con query che possono essere anche
simultanee. Quindi occorre considerare anche il Problema
organizzazione degli archivi in ambiente multiutenza, e
per questo si possono utilizzare:
2. Soluzioni di tipo tradizionale ossia archivi indicizzati
(file indexati)
applicazioni del Modello teorico di file indexato di
Wirth (lucido 60) e Sistema di Indici.
Per rientrare nel contesto tradizionale si riparte dalle
considerazioni fatte in Parte1 (luc. 106) sull’
organizzazione degli archivi estendendole:
Archivio insieme di record contraddistinti da una
chiave (primaria) e tanti campi (attributi) tra cui possono
esserci chiavi secondarie. Ogni attributo puo’ essere una
chiave secondaria che generalmente identifica
non un solo record, ma un gruppo di record per es.
“Professione” per un archivio di Cittadini con chiave
primaria “Codice_Fiscale”.
Archivio
Archivio Inverso insieme
di attributi indicizzati
y = f(x)
x = f -1( y)
libro=Archivio(informazione)
informazione=Archivio-1 (libro)
Indice
Indice completo = Archivio completamente invertito
116
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
File invertito scambio di ruolo tra record e attributi, da
usare insieme all’ originale per non avere
troppe difficolta’ nella gestione
mentre nell’ archivio la chiave primaria
identificava un gruppo di campi ( al record), nell’
archivio invertito un campo (chiave secondaria)
identifica un gruppo di record ossia di chiavi primarie.
Evoluzione Archivi:
sequenziali: ordinati per chiave primaria; per
usare una delle chiavi secondarie occorre
uno specifico ordinamento per la chiave
secondaria scelta, con conseguente lentezza
d’ uso;
ad accesso diretto: costruiti in funzione della
chiave primaria
hashing: veloce reperimento record,
ma solo accesso selettivo,
NO sequenziale
funzione Indice: si puo’ costruire su ogni
Attributo (Archivio
completamente invertito)
Esigenza: Sistema di indici snello
117
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
118
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
119
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Considerazioni su archivi & indici in ambiente a
multiutenza accessi concorrenti di processi ad una
struttura a b*tree di ordine k che implementa l’ indice.
lettura
Processi{
modifica
Problema:
permettere a +processi di accedere simultaneamente all’
indice salvaguardandone l’ integrita’.
Soluzioni:
1. +semplice: serializzare in modo stretto tutti i Processi
di modifica imponendo un lucchetto sull’ intero
b*tree. Ogni modificatore (anche di solo 1 termine)
deve ottenere il controllo sull’ intero b*tree una
volta ottenutolo inibisce l’ accesso ad ogni altro
modificatore fino alla fine del suo lavoro; l’ accesso
simultaneo e’ consentito solo a Processi di lettura
SOLUZIONE SODDISFACENTE SOLO SE il
#accessi concorrenti e’ basso rispetto ad attivita’
globale.
2. –semplici: attivare un lucchetto sulla singola pagina
del b*tree inibendone l’ accesso finche’ non e’
accertata la condizione di
integrita’ {
a cancellazione avvenuta deve risultare m k (*)
” inserzione
“
“
“
m 2k (*)
I lucchetti sono
posti da uno Schedulatore delle richieste secondo un ordine
FIFO consultazioni +rapide, ma ATTENZIONE ai
DEAD-LOCK !!
(*) m = #termini presenti nella pagina
120
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Problema accessi concorrenti & Soluzioni tratte da Bayer
& Schkolnick (Acta Informatica 1977) illustrate con i
successivi esempi dove per fissare le idee si considera il
seguente b*tree (con k=2 e h=3 e nelle foglie chiavi tra
parentesi che sintetizzano anche le info.)
10000
20
40
10020
8
11110
14
20
27
40 60 80 90
10050
(8) (9) (11) (12)
(8) (9) (11) (12)
(1) (3) (4)
(14) (17)
11120
(32) (34) (36) (38)
(40) (48)
Integrita’ 8)della pagina in inserzione: m 2*k; in
cancellazione: m k
Attivazione lucchetti di protezione, anche inibitori di altri
processi per raggiungere l’ OBIETTIVO dell’ alta concorrenza.
lettura
Esistono 2 tipi di lucchetti di protezione
scrittura
compatibile con altri (condiviso)
incompatibile “ “
(esclusivo)
“
“ “
“
Es. Si consideri l’ inserimento nel b*tree di (49)
finche’ non e’ raggiunta la pagina 11120 non si puo’ dire
se la pagina 11110 sara’ integra occorre un lucchetto
su 11110 fino a che non e’ stato verificato che la
modifica su 11120 non propaghera’ split ossia che nella
pagina 11120 risulti m 2*k.
…ma e’ obbligatorio o basta ?
121
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Attenzione ai deadlock !!
Considerata la porzione di b*tree
40 60 80 90
qui a fianco, si considerino 2
processi u1 con lucchetti 1 e 1
(32) (34) (36) (38)
e u2 con lucchetti 2 e 2 .
Il processo u1 vuole inserire l’ informazione di chiave 39
ossia(39).
Per farlo il codice potrebbe essere cosi’ fatto:
…. Attiva 1 su pagina(_padre)
Leggi pagina(_padre)
Attiva 1 su pagina(_figlio)
Leggi pagina(_figlio)
If (not integrita’ pagina(_figlio))
then disattiva 1 & attiva 1 su pagina(_padre)...
Se durante l’ analisi di integrita’_figlio subentra il processo u2 che
vuole leggere pagina(_figlio), u2 pone 2 su pagina(_padre) e cosi’
inibisce l’ attivazione di 1 da parte di u1… e cosi’ u1 aspetta u2 che
aspetta u1…
Schema libero da deadlock valido per ogni pagina:
…. Attiva 1 su pagina
Leggi pagina
Attiva 1 su figlio
Leggi figlio
If (integrita’ figlio) then disattiva 1 da pagina
& attiva 1 su “
A questo punto (1 e’ disattivato) il processo u2 puo’ porre 2
(compatibile con 1) sulla pagina padre e partire .………….
ma l’ iniziale 1 non e’ troppo restrittivo? … e allora soluzioni
con +tipi di e di ma con complessita’ maggiore!!
Quelli presentati sono semplici esempi di metodi di protezione
attuati su b*tree valevoli anche per i b+tree. … ma come sono
realizzati nei DBMS i metodi di protezione?
122
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Per rispondere occorre considerare il Collegamento con i
DBMS ed il File System in modo da poter ritrovare applicati
tanti meccanismi e metodi presentati con le strutture dati.
Nei DBMS e’ il Gestore o controllore della
concorrenza ad attuare i metodi di protezione: come
indicato nella parte 2 si tratta di un modulo del DBMS
(detto anche genericamente Scheduler) che stabilisce se
le richieste di lettura/scrittura sul d.b. sono ammissibili o
no. Prima di parlare dello Scheduler, si comincia con la
descrizione del comportamento del DBMS rispetto alle
strutture dati viste, in modo che questa parte sia di
collegamento con le precedenti. E’ gia’ stato indicato che
le strutture dati piu’ interessanti negli RDBMS sono
quelle di tipo gerarchico che permettono operazioni di
ricerca e modifica in modo efficiente. Un indice definito
dall’ utente su un attributo o piu’ attributi di una tabella
viene implementato con un struttura di tipo b*tree (o
b+tree). Nei DBMS esistono comunque anche strutture
sequenziali e calcolate con “hashing” di chiave.
Si e’ gia’ detto poi che le operazioni di I/O su disco in
ambiente NON distribuito possono anche essere
effettuate tramite il File System (F.S.) dal DBMS col
Buffer Manager che lo integra. Il DBMS “attiva” il
Buffer Manager che si occupa di caricare/scaricare le
pagine in/da C.M. Per caricare/scaricare le pagine in/da
C.M. il DBMS utilizza una zona di C.M. di grosse
dimensioni, un buffer, organizzato in pagine, ciascuna
con dimensione pari ad un multiplo della pagina (o
blocco) di disco, preallocato dal DBMS e condiviso tra
le varie transazioni. Le richieste di lettura e scrittura
fisica sulla memoria secondaria sono però realizzate dal
Gestore della stessa con le primitive opportune.
123
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
“Correlazioni” tra F.S. e Buffer Manager:
le primitive di F.S. relativamente ad un file sono:
create, delete, open, close, read, read-seq, write, write-seq,
con read e write che si riferiscono a 1 blocco = pagina di
memoria di massa.
Nei DBMS il Buffer Manager (con il Controllore dell’
affidabilità che deve garantire Atomicità e Durability
delle delle transazioni) puo’ usare queste funzioni, ma
anche altre. Per es. quando la transazione in esecuzione
richiede un’ informazione su una pagina di un file, il
Buffer Manager puo’ usare la primitiva fix che effettua la
ricerca della pagina nel buffer di C.M. Spesso la trova
(per il principio di localita’ usato nei Sistemi Operativi
per l’uso della Memoria Virtuale: “i dati referenziati di recente
hanno alta probabilità di essere riutilizzati”) e la riserva
per la transazione, ma in caso di insuccesso “tenta” di
leggere un’ altra pagina dalla memoria secondaria.
Tenta perche’ prima occorre far posto nel buffer il
Buffer Manager deve scaricare (per es. con la primitiva
flush) dal buffer una pagina “vittima” scelta tra quelle
gia’ rilasciate da un’ altra transazione.
Tenta perche’ prima occorre stabilire che le operazioni
di lettura e scaricamento non siano in conflitto con altre
operazioni … funzione dello Scheduler …
Altre primitive dei DBMS sono: unfix per rilasciare una
pagina; use per confermare la pagina “fixata” come
pagina valida per la transazione attiva; force e flush per
trasferire pagine in memoria di massa.
Queste primitive sono innescate dal metodo di accesso (
modulo di ®DBMS detto Gestore dei metodi di accesso)
specifico dell’ organizzazione fisica dei dati.
124
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
L’ architettura di ®DBMS descritta da Atzeni & …ed.1999 e’
rappresentata nelle fig. 9_11, 9_15 e successive fuse e
schematizzate in Appendice della parte 2 e riportato qui di
seguito. Vi si notano alcuni metodi di accesso tra cui per es. il
B+tree manager.
Appendice parte 2
A
L
T
R
I
M
O
D
U
L
I (*)
Gestore Metodi
di Accesso
Sc
an
Ma
na
ger
B+
Tree
Man
ager
Buffer
Manager
Scheduler
Primitive
del File_
System e/o
del
D.B.M.S.
d.b.
DBS
Tab.dei
lock
LOG
Schema di architettura dei DBS relativa all’ accesso al d.b. estendibile
anche al contesto client-sever (da Atzeni &… Fig. 9.1 - 10.1 ed. 1999)
preferibile al tipo adottato nel 2003 per la sua completezza nella
schematicità.
Comunque qui di seguito c’è anche la sintesi degli Schemi di Atzeni
&… dell’ ultima edizione.
( * ) Tra gli ALTRI MODULI ci sono l’ Ottimizzatore (a monte del
Gestore dei Metodi di accesso) ed il Controllore dell’ affidabilita’ con
procedure di ripristino in caso di malfunzionamento (a valle). Il gestore
della Memoria secondaria è schematizzato nel blocco a destra.
125
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Gestore Query e aggiornamenti -- Gestore delle transazioni
|
|
Gestore dei Metodi di accesso——Scheduler--Gestore affid.
|_______________________|
|
Gestore del Buffer
|
Gestore memoria secondaria
|
B.D.
Log
Sintesi delle componenti di un DBMS coinvolti nella gestione di
interrogazioni e transazioni da Atzeni & … ed. 2003
126
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Organizzazione delle pagine, Gestore dei metodi di
accesso & Scheduler
Molto sinteticamente: i metodi di accesso (che
aggiornano/leggono informazioni) sono in grado di
conoscere la disposizione e l’organizzazione delle tuple
nelle pagine (= blocchi di disco).
Ogni pagina oltre alle informazioni (dati, tuple per
RDBMS) utili per l’utente contiene informazioni di
controllo sia per il F.S. (o per il Buffer Manager) sia per
il metodo di accesso. Queste sono: la parte iniziale e
finale (block-header & block-trailer, page-header &
page-trailer con informazioni rispettivamente per il
Buffer Manager e per il Metodo di accesso). Dentro la
pagina le informazioni, i dati utili all’ utente sono
organizzati nel modo previsto dalla struttura di
appartenenza ossia b(*/+)-tree (di cui si e’ gia’ parlato) o
strutture sequenziali o calcolate. Comunque ogni pagina
generalmente contiene un dizionario di pagina con
puntatori ai dati, (per es. alle tuple cfr. fig.9.16 di Atzeni
& …ed. 1999 fig.1.2 vol.2 ed. 2003 ed anche schema del
lucido 117 di questa parte) e poi eventuali puntatori ad
altre pagine (precedenti o successive nella struttura dati
utilizzata), contatori, controlli di parita’… Scopo ovvio
di tali indicatori e’ il recupero rapido e corretto di
qualunque informazione utile per l’utente (per es. un
attributo in una tupla).
La lettura/scrittura di ogni pagina prima di essere attuata
deve passare dal filtro dello Scheduler (o Gestore della
concorrenza di cui si e’ gia’ accennato in Parte 2 e
relativamente all’ integrita’ dei b*tree) che stabilisce se
l’ operazione e’ in conflitto con altre operazioni.
127
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
(E con architetture distribuite cresce la complessita’ dello
Scheduler….)
In Atzeni & … la teoria del controllo di concorrenza e’
trattata in ambienti non distribuiti e distribuiti nei
capitoli 9 e 10 ed. 1999 cap. 1, 2, 3 vol.2 ed. 2003, ossia
in dettaglio. Qui si evidenzia l’ essenzialità.
Tra i metodi illustrati per il controllo della concorrenza,
quello piu’ usato in pratica (e per tale motivo anche
descritto con esempi relativi ai b*tree) e’ il locking
la gestione dei lock e’ effettuata dal Lock Manager,
parte fondamentale dello Scheduler. L’ idea su cui si
basa e’ che ogni operazione di lettura/scrittura deve
essere protetta da primitive di tipo r-lock per la lettura e
w-lock per la scrittura. Queste devono precedere ogni
operazione di lettura/scrittura che deve essere seguita da
una primitiva un-lock.
Il lock (come gia’ noto dagli esempi sui b*tree) puo’
essere esclusivo (non puo’ coesistere con altri lock) o
condiviso e le relative richieste devono essere
automaticamente fatte dal processo che genera la
lettura/scrittura tipicamente dal metodo di accesso.
Il Lock Manager concede i lock sulle pagine (in
generale sulle risorse) in base:
al loro stato di cui tiene conto in una tabella di lock
riportata di seguito da Atzeni & …;
ed al contatore cont dei lock di ogni risorsa che e’
incrementato ad ogni concessione di r_lock sulla
risorsa e decrementato ad ogni relativo unlock.
128
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Stato delle Risorse
r_locked
w_locked
Richieste
Libero
OK / r_locked OK / r_locked
r_lock
w_lock
unlock
OK/ w_locked NO/ r_locked
Error
NO/ w_locked
NO/ w_locked
OK / libero o OK / libero
r_locked se cont >0
tabella dei lock
Dalla tabella dei lock si nota che, come gia’ indicato, c’e
compatibilita’ solo tra i lock di lettura
si possono sommare e quando ne e’ rilasciato 1, la
risorsa puo’ essere libera o ancora bloccata se il suo
contatore resta > 0.
Il Lock Manager deve anche assicurarsi che le
operazioni di lettura/scrittura seguano un ordine
temporale in modo che la loro sequenza sia logicamente
serializzabile ( NO aggiornamento di una pagina
prima della sua lettura, per esempio !)
Gli eventi temporali possono essere ordinati con
indicatori i timestamp (gia’ nominati nelle parti
precedenti) che sono indicatori associati alle transazioni e
memorizzano gli istanti iniziali delle transazioni permettendone
un ordinamento e controllo temporale. Un metodo che usa i
timestamp e’ il controllo della concorrenza mediante
timestamp (T.S.) anche se facile da realizzare (specie
in sistemi centralizzati tramite l’ orologio del sistema),
produce molti abort di transazioni, superabili solo
replicando i dati da aggiornare.
129
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
In generale il metodo +diffuso e’ quello che usa il
protocollo di locking a 2 fasi che sembra sufficiente a
garantire la sequenza logicamente serializzabile di
ogni transazione.
La regola relativa e’:
ogni transazione dopo aver rilasciato un lock non ne
puo’ aquisire altri
Con questo tipo di controllo sui lock si evidenziano
due fasi nell’ esecuzione della transazione: quella in
cui si richiedono e (se il Lock Manager li concede)
acquisiscono i lock sulle risorse necessarie all’
esecuzione della transazione, e quella successiva in cui
si rilasciano i lock posti
Con transazioni che seguono questi criteri (e si dicono
“benformate rispetto ai lock”) e le relative restrizioni si
realizzano sistemi transazionali.
Il protocollo di locking a 2 fasi specifica che i lock
acquisiti all’ inizio di ogni transazione sono rilasciati
solo al termine della transazione dopo che ogni dato e’
stato portato al suo stato finale.
Si puo’ comunque arrivare al blocco critico che si
verifica quando 2 transazioni non possono procedere
perche’ le richieste dei lock da loro effettuate bloccano
reciprocamente le risorse che le 2 transazioni vorrebbero
usare. Una “soluzione” al blocco critico e’ il time-out
dopo un tempo prefissato una delle 2 transazioni
e’ abortita.
130
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Ogni problema diventa comunque +complesso quando si
passa all’ ambiente distribuito
In questo caso una transazione puo’
coinvolgere +Server facendo uso delle risorse
relative a ciascuno di loro.
Atzeni & … fanno un esempio relativo ad un sistema
bancario dove la relation
ContoCorrente(CC#, Nome, Saldo)
si ipotizza frammentata tra 2 nodi della rete (le prime
10000 tuple su uno, le successive su un altro). Quindi la
transazione che segue si riferisce a 2 Server:
begin transaction;
w_lock1(ContoCorrente1)
w_lock2(ContoCorrente2)
update ContoCorrente1
set saldo = saldo -1000 where CC# = 1111;
update ContoCorrente2
set saldo = saldo +1000 where CC# = 19814
commit work;
unlock1(ContoCorrente1)
unlock2(ContoCorrente2)
end transaction;
e DEVE essere “COMPIUTA” interamente! !!
Perché ? per l’ Atomicità delle transazioni, proprietà che
deve essere garantita anche in ambiente distribuito. Per
garantire l’ Atomicità si fa uso del protocollo di commit
a 2 fasi che permette il “compimento” o l’ abort di ogni
transazione ed in ambiente distribuito funziona nel modo
seguente.
131
Anna Maria Carminelli Gregori: Appunti su d.b. parte3 A.A. 2005
Il controllo delle risorse di ogni Server spetta ad un
Processo tipico di ogni Server: il Resource Manager
(R.M.) che con il protocollo di commit a 2 fasi, nella
prima fase, contrassegna con r-lock o w-lock le risorse
richieste dalla transazione.
Pero’ la prenotazione e’ resa effettiva da un altro
Processo, il Transaction Manager (T.M.) del DBMS
che coordina le transazioni concorrenti. Questo puo’
essere il DBMS del Client che fa la richiesta o del
Server al quale il Client invia la richiesta e che come
“Coordinatore” smista la relativa transazione ad altri
Server “Partecipanti”.
T.M. scambia messaggi con gli R.M. di tutti i Server
coinvolti: solo se tutte le risposte indicano che le risorse
sono in stato di pronto (ready) la transazione puo’
iniziare, altrimenti e’ abortita.
In questa fase l’ abort puo’ essere provocato anche da
assenza di messaggi tra R.M. e T.M. e/o da guasti.
Nella seconda fase (finale) la transazione puo’ essere
completata solo se tutti gli R.M. coinvolti comunicano
esito positivo
il T.M. risponde con l’ esito finale della transazione.
SE mancano alcuni messaggi degli R.M. si ha la
ripetizione delle trasmissioni da parte del T.M.
SE si verifica un guasto nel T.M. le risorse bloccate
dagli R.M. restano bloccate … fino ad un global abort.
Tutte queste considerazioni e analisi sono solo una breve
sintesi delle Soluzioni al Problema organizzativo di archivi
in ambiente multiutenza.
Fine
132

![Via Eugenio Barsanti, 24 - 00146 Roma Telefono [Fax] 06](http://s1.studylibit.com/store/data/004164020_1-c5a7c8484d07a6b1f1c9ad8187f8cd02-300x300.png)








