Progetto di un filtro FIR

Caratteristiche di un filtro ideale
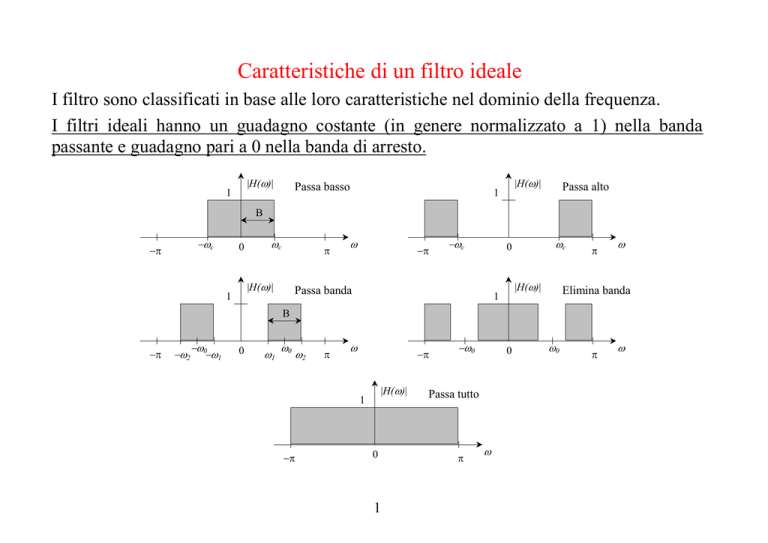
I filtro sono classificati in base alle loro caratteristiche nel dominio della frequenza.
I filtri ideali hanno un guadagno costante (in genere normalizzato a 1) nella banda
passante e guadagno pari a 0 nella banda di arresto.
|H()|
1
Passa basso
|H()|
1
Passa alto
B
c

0
c

|H()|
1


c
c
0
Passa banda
|H()|
1


Elimina banda
B

2
0
1
0
1
0
2



|H()|
1

0
1
0
0
Passa tutto


0


Un filtro ideale ha risposta in fase lineare.
Esempio: si assuma che un segnale con componenti in frequenza contenute
nell’intervallo (1,2) sia inviato in ingresso a un filtro con risposta in frequenza:
1     2
Ce  jn0
H ( )  
0
altrove
con C e n0 costanti. Il segnale in uscita è:
Y ( )  X ( ) H ( )  CX ( )e  jn0
1     2
Nel dominio del tempo, l’uscita assume la forma: y(n) = C x(n - n0)
E’ ritardata rispetto all’ingresso (a parte il fattore di scala determinato dalla costante C).
In genere un ritardo è tollerato nella maggior parte delle applicazioni e non comporta
distorsione sul segnale.
Un filtro ideale ha una fase lineare nella sua banda passante:
() = - n0
d( )

(

)


La derivata della fase rispetto ad  ha le dimensioni di un ritardo g
d
Se g() = n0 = costante, tutte le componenti in frequenza acquisiscono il medesimo
ritardo passando attraverso il filtro.
2
Progetto di filtri digitali
▪ Definizione delle specifiche nel dominio della frequenza: ampiezza e fase richieste.
▪ Calcolo dei coefficienti di un sistema FIR o IIR che approssimi con la precisione
desiderata la risposta in frequenza desiderata
I filtri FIR sono utilizzati quando si abbia la necessità di avere un sistema con fase lineare
nella banda passante. Un filtro IIR infatti può solo approssimare una fase lineare.
Un filtro IIR, a parità di ordine, è più selettivo di un filtro FIR.
Esistono ausili software che a partire dalla maschera del filtro, permettono di ottenere
l’ordine necessario ed il set di coefficienti che devono essere utilizzati.
▪ Analisi degli effetti della quantizzazione (# finito di bit).
Effetti sulla funzione di trasferimento implementata, instabilità o cicli limite negli IIR
▪ Scelta dell’architettura (potenza, velocità, effetti della quantizzazione)
▪ Ottimizzazione della realizzazione hardware.
Scelta di sommatori, moltiplicatori, applicazione tecniche pipelining o parallelismo
▪ Attenzione nella fase di layout.
3
Caratterizzazione di un filtro reale
Il principio di causalità vieta che la caratteristica H() di un filtro possa essere
identicamente nulla, se non su un numero finito di punti e che la pendenza della
transizione tra banda passante e banda di arresto sia infinita.
Nelle realizzazioni pratiche, un filtro ideale non è necessario, basta approssimarlo:
si tollera
|H()|
▪ un ripple in banda passante
1+1
▪ una transizione di pendenza finita tra
1-1
la banda passante e la banda di arresto
▪ un valore diverso da zero nella banda
banda di
di arresto.
transizione
2
0
p
banda passante
4
s
banda di arresto


Progetto di un filtro FIR
 un filtro FIR può essere descritto da una equazione alle differenze:
M
y(n)  b0 x(n)  b1 x(n-1 )    bM-1 x(n-M  1 )   bk x(n  k )
k 0
 tramite la convoluzione della risposta impulsiva del sistema con l’ingresso:
M
y(n)   h(k ) x(n  k )
k 0
 mediante la funzione (polinomio di grado M nella variabile z-1)
M
H ( z )   h( k ) z  k
k 0
Un filtro FIR ha fase lineare se è simmetrico o antisimmetrico:
h(n)=  h(M-n),
per n = 0, 1, . . . , M
dalla condizione di simmetria o antisimmetria si ricava:
z-M H(z-1)=  H(z)
5
z-MH(z-1)=  H(z),
le radici del polinomio H(z) sono identiche alle radici del polinomio H(z-1), quindi le
radici compaiono in coppie reciproche (se zi è una radice, anche 1/zi lo è).
h(n)  le radici complesse compaiono in coppie complesse coniugate, quindi se zi è una
radice di valore complesso, anche zi* è una radice (e quindi anche 1/zi*)
La risposta in frequenza H() di un filtro FIR a fase lineare è ottenuta valutando H(z) sul
cerchio di raggio unitario.
piano z
cerchio di raggio
unitario
1/z*3
z3
1/z*2
z2
z1
1/z1
z*2
z*3
1/z2
1/z3
6
Progetto di un filtro FIR a fase lineare mediante il metodo “a finestra”
Si suppone di conoscere la risposta desiderata per il filtro Hd(). Si ricava hd(n):
1
hd (n) 
2
Data una Hd(


H d ( ) e jn d

hd(n) ha durata infinita, e non può essere implementata con un FIR.
E’ allora necessario troncare hd(n) ad una certa lunghezza M.
Il troncamento equivale a moltiplicare hd(n) per una finestra rettangolare:
n  0, 1,  M
altrove
1
w(n)  
0
La funzione h(n) risultante è:
hd (n)
h(n)  hd (n)w(n)  
0
n  0, 1,  M
altrove
A causa del troncamento, H() sarà differente da Hd(
7
Moltiplicare hd(n) w(n) equivale, in frequenza, alla convoluzione Hd(
1
H ( ) 
2


M
W ( )   w(n) e  jn  e  jM / 2
H d (v)W (  v)dv
n 0

W()
sin( M / 2)
sin( M / 2)
|W()
|
0 dB
M=21
M=41
-50 dB
0
H(
H(
0.1f
0.5f
M, l’effetto viene ridotto)
a delle oscillazioni (ringing).
Finestre alternative (Bartlett, Blackman, Hamming, Hanning, etc).
Svantaggio: posizione delle frequenze p e s difficile da controllare
8
Progetto di un filtro FIR a fase lineare equiripple ottimizzato
“ottimo” perché l’errore commesso approssimando la funzione di trasferimento voluta
viene (in modo pesato) equamente diviso tra banda di transizione e banda oscura.
Per un sistema simmetrico o antisimmetrico di ordine M:
H ( )  H r ( )e  jM / 2
H ( )  H r ( )e j[ M / 2 / 2]
Le funzioni Hr() sono a valori reali (differenti se è simmetrico, antisimmetrico, con M
pari o dispari: 4 casi).
E’ possibile generalizzare:
P( ) 
H r ( )  Q( ) P( )
L
 (k ) cosk
k 0
Gli (k) sono i parametri del filtro, legati linearmente alla risposta h(n) del filtro.
La funzione Q() ed il limite di somma L dipendono dalla simmetria e dall’ordine (pari
o dispari) del filtro, ma sono indipendenti dalla sua risposta impulsiva.
La soluzione del problema (trovare i coefficienti (k)) consiste nel minimizzare l’errore:
E() = W() [Hdr() - Hr()] = W()[Hdr()-Q()P()]
9
E() = W() [Hdr() - Hr()] = W()[Hdr()-Q()P()]
Hdr() è la funzione target (ideale: 1 nella banda passante e 0 nella banda di arresto)
W() è una funzione che rappresenta il peso dell’errore tollerato nelle due bande.
Per un filtro passa basso:
1-1  Hr()  1+1
-2  Hr()  2
in banda passante
in banda oscura
W() è definita per comodità come “peso normalizzato”:
W() = 2/1
in banda passante
W() = 
in banda oscura
Problemi:
▪ esistenza della soluzione (“approssimazione di Chebyshev”: identifica le condizioni
necessarie e sufficienti che garantiscono che il problema di minimizzazione presenti
un’unica soluzione)
▪ come calcolarla (sistema non lineare che viene risolto mediante l’algoritmo di Remez)
▪ come calcolare M (problema aperto)
10
Progetto di un IIR tempo discreto a partire da un filtro tempo continuo
E’ uno dei metodi possibili. Perché?
 la progettazione di filtri analogici è una tecnica consolidata da decenni
 esistono metodologie e tools di progettazione che risolvono il problema
conviene quindi progettare nel dominio analogico, e poi passare al dominio campionato.
Modi per descrivere un filtro analogico lineare tempo invariante:
M
B( s )
H a ( s) 

A( s)
 s
k
 s
k
k 0
N
k 0
k

H a ( s)   h(t )e st dt
k

d k y (t ) M
d k y (t )
k
  k

k
dt
dt k
k 0
k 0
N
Dai differenti modi di rappresentare un filtro analogico derivano differenti metodi per
convertire il filtro analogico in un filtro a valori discreti nel tempo
Differenti metodi = differenti relazioni tra s e z.
Requisiti della trasformazione s -> z ?
11
Requisiti della trasformazione s -> z
Un filtro analogico tempo invariante è stabile se tutti i poli della funzione di
trasferimento Ha(s) che lo caratterizza sono situati nel semipiano sinistro del piano s.
Si vuole allora che la conversione analogico-digitale rispetti le seguenti regole:
1. stabilisca una corrispondenza tra l’asse j del piano s e il cerchio |z| = 1 del piano z, in
modo da stabilire una relazione diretta tra le variabili “frequenza” nei due domini;
2. trasformi i punti s > 0 in punti |z| < 1 in modo che un filtro analogico stabile venga
convertito in un filtro digitale stabile.
Attenzione: non è possibile progettare un filtro IIR causale e stabile con fase lineare.
E’ possibile infatti dimostrare che la fase lineare richiede:
H(z) =  z-N H(z-1)
Ma questo sistema ha per ogni polo con |zp| < 1, un polo corrispondente con |zp| > 1
quindi sarebbe un sistema instabile.
E’ per questo che quando in un’applicazione viene richiesta una fase rigorosamente
lineare, il filtro che viene prescelto è un filtro FIR.
12
Primo metodo di progettazione: approssimazione delle derivate
nell’equazione differenziale lineare con un’equazione alle differenze
Sostituzione di derivate con rapporti incrementali all’indietro (backward difference):
dy(t )
y (nT )  y (nT  T ) y (n)  y (n  1)


dt t nT
T
T
dy 2 (t )
d  dy(t ) 
y (n)  2 y (n  1)  y (n  2)


dt 2 t nT dt  dt  t nT
T2
nel tempo
dy(t )
dt
d 2 y (t )
dt 2
d N y (t )
dt N
in s
in z
H a (s)  s
1  z 1
H ( z) 
T
H a ( s)  s 2
 1  z 1 

H ( z )  

 T 
H a ( s)  s N
 1  z 1 

H ( z )  

 T 
13
2
N

1  z 1
s
T
z
1
1  sT

H ( z )  H a ( s) s  1 z 1
T
Proprietà del filtro determinate dalla trasformazione:
sostituendo s = j (= pulsazione angolare nel dominio analogico) si ricava
l’equazione della curva nel piano z che corrisponde all’asse immaginario del piano s:
z
1
1
T


j
1  jT 1   2T 2
1   2T 2
Al variare di da – a +, nel piano z si ha un cerchio di r = 1/2 con centro in (1/2,0)
j
cerchio di raggio
unitario
1/2
piano z

piano s
filtro stabile nel dominio tempo continuo  filtro stabile nel dominio tempo discreto.
I poli del filtro digitale sono in una regione estremamente ridotta: si realizzano filtri
passa basso e filtri passa banda con frequenze di risonanza limitate
14
Secondo metodo di progettazione: trasformazione ad impulso invariante
ha(t): risposta impulsiva del filtro tempo continuo con funzione di trasferimento Ha(s)
si progetta un filtro IIR con risposta impulsiva h(n) che è il campionamento di ha(t)
h(n)  ha (nT) 

|Ha(T)|
 h (t ) t  n
a
n  
1 
   2k 
H ( ) 
Ha

T k   T


MAX
Lo spettro della risposta impulsiva
campionata è la replica della risposta
impulsiva del filtro tempo continuo.
MAX

|H(T)|
MAXT
Se fs = 1/T < 2 fMAX dello spettro della
risposta impulsiva del sistema analogico
di partenza si ha aliasing.
15
MAXT
 T
Come si corrispondono s e z?
da z = esT

2k 

Ha  s  j

 

k  
esprimendo s =  + j e z = r ej si ottiene: r = eT e
H ( z ) z e s
1

T

se  < 0  0 < r < 1,
se  > 0  r > 1
se  = 0 si ha r = 1: l’asse
immaginario del piano s viene
posto in corrispondenza con il
cerchio di raggio unitario nel
piano z
 = T
j
piano z
3j

T
j

T
piano s
cerchio di raggio
unitario

la trasformazione non è
biunivoca: ej = ejT comporta
 = T a meno di uno
sfasamento pari a 2.
16
-j

T
-3j

T
Come si posizionano i poli?
Esprimendo Ha(s) in forma frazionaria, e supponendo, per semplicità, i poli singoli:
H a (s) 
N

k 1
ck
s  pk
N

 ha (t ) 
ck e p k t
per t  0
k 1
Campionando ha(t) in modo periodico, cioè per i tempi t = nT si ha:
h(n)  ha (nT ) 
N

ck e pk nT
per n  0
k 1
H ( z) 


n 0
h( n) z
n
  e
N
 N
pk nT   n
z 
 
ck e
ck

n 0  k 1
k 1



H ( z) 

pk T
z

1 n
n 0
N
 1 e

  pkT 1

e z

 n 0

n



pkT 1 
1 e z 
1
ck
k 1
pk T
z 1
Il filtro digitale ha quindi poli nei punti zk = epkT, per k = 1, 2, . . . , N
Anche questa trasformazione è indicata per il progetto di filtri passa basso e passa banda,
per limitare gli effetti dovuti all’aliasing, T deve essere sufficientemente piccolo,
17
Terzo metodo di progettazione: trasformazione bilineare
Scopo: trasforma in modo biunivoco tutto l’asse j nel cerchio |z| = 1 (annulla aliasing)
j
piano s
j’
j

T

piano s’
piano z
2  1  z 1 

s  
1 
T 1 z 
’
-j

T
cerchio di
raggio unitario

2
r 2 1

s    j z  re :   
2
T  1  r  2r cos  
j

2
2rsin 



2
T  1  r  2r cos  
r < 1   < 0: sistema tempo discreto stabile a partire da un sistema tempo continuo stabile
r 1   0



2  sin   2


  tan
T  1  cos   T
2


2
T
-10?


2

10?
  2 tan 1
T
2
Tutto l’asse  viene posto in corrispondenza
biunivoca con l’intervallo [-, ].
La relazione è non lineare, tranne che WT  1
Le frequenze del sistema analogico vengono
compresse nel passaggio (frequency warping).
18
Progetto “diretto” di filtri IIR
Progetto diretto di filtri IIR nel dominio della frequenza
Si definisce una procedura che ottimizzi i parametri che caratterizzano i filtri.
Funzione di trasferimento del filtro IIR come cascata di celle di ordine 2:
K
1   k1 z 1   k 2 z 2
H ( z)  G
1
2
1


z


z
k 1
k1
k2

il parametro G (guadagno del filtro) e i coefficienti k1, k2, k1, k2, devono essere
determinati durante il processo di ottimizzazione.
Risposta in frequenza del filtro:
1
2
K
1


z


z
k1
k2
H ( )  G A( ) e j( )
A( )  
1
  k 2 z  2 z e j
k 1 1   k 1 z
() è la risposta in fase.
Ritardo di inviluppo g():
 g ( )  
d( )
d
 g ( )   g ( z ) z  e   
j
19
d( z )
dz
dz z  e j d
Si suppongano A() e g()specificati per le pulsazioni 1, 2, . . . L, (0  ||  ).
per la pulsazionel: guadagno desiderato Ad(l), ritardo di inviluppo desiderato g,d(l)
Errori commessi sull’ampiezza e sul ritardo di gruppo
 A (l )  G A(l )  Ad (l )
  (l )   g (l )   g (0 )   g ,d (l )
total weighted least-squares error:
 (coefficienti, G )  (1   ) p Al GA( l )  Ad ( l )    pl  g ( l )   g ( 0 )   g ,d ( l )2
L
L
2
l 1
l 1
 è funzione dei coefficienti (cioè di tutti gli k1, k2, k1, k2) e del guadagno G, che
sono i parametri che dovranno essere fatti variare per rendere minimo l’errore
i pesi , pAl e pl sono definiti dal progettista
L
Il guadagno G che minimizza l’errore è
Gˆ 
p
l 1
L
p
l 1
20
 l ) Ad ( l )
Al A(
Al A
2
( l )
Rimane una funzione non lineare di 4K (K = # celle biquadratiche) parametri:


 (coefficienti, Gˆ )  (1   ) p Al Gˆ A( l )  Ad ( l )    pl  g ( l )   g ( 0 )   g ,d ( l )2
L
L
2
l 1
l 1
Da minimizzare!
La soluzione viene ricercata iterativamente:
a)
si assume un valore iniziale dei coefficienti
b)
si calcola il valore dell’errore
c)
si calcolano le derivate parziali dell’errore nel punto calcolato rispetto a tutti i
coefficienti
d)
si modificano i coefficienti nel senso che permette di diminuire l’errore
e)
si calcola la differenza  tra i due errori calcolati successivamente
f)
si esce (se  è sufficientemente piccolo) o si itera ripartendo dal punto b)
Problema: si può convergere verso un minimo locale!
21
Implementazione di sistemi FIR e IIR
complessità computazionale, quantità di memoria richiesta, effetto della quantizzazione,
inserimento in una struttura parallela, inserimento di una pipeline.
Forma diretta I e II
x(n)
b0
y(n)
z-1
x(n)
b0
z-1
b1
z-1
-a1
z-1
-a1
z-1
b2
z-1
-a2
z-1
-a2
z-1
bM-1
b2
z-1
-aN-1
z-1
b1
-aM
bM
z-1
bM
-aN
z-1
-aN
Difetto: sensibile alla quantizzazione dei parametri
22
y(n)
signal flow graph
grafo che rappresenta il flusso del segnale nella struttura: modo alternativo alla
rappresentazione mediante diagrammi a blocchi
Elementi base: rami e nodi:
segnale in uscita al ramo = segnale di ingresso per il guadagno del ramo o per z-1
segnale in un nodo = somma di tutti i segnali dei rami che entrano nel nodo
punti di diramazione = nodi dai quali partono rami sui quali viene replicato il segnal
x(n)
b0
y(n)
x(n)
b0
z-1
z-1
-a1
-a1
b1
z-1
-a2
b2
-a2
z-1
b2
-aM
z-1
bM
-aN
z-1
-1
z
-aM
b1
bM
z-1
-aN
23
y(n)
Teorema della trasposizione: invertendo la direzione su tutti i rami e scambiando
ingresso ed uscita, la funzione di trasferimento del sistema non cambia.
Struttura (o forma) trasposta:
x(n)
source
node
b0
z-1
-a1
b1
y(n)
y(n)
sink
node
sink
node
b0
z-1
-a1
b1
-a2
z-1
b2
-a2
z-1
b2
-aM
z-1
bM
-aM
z-1
bM
-aN
z-1
-aN
z-1
Forma diretta II
Forma trasposta II
24
x(n)
source
node
Forma diretta II
x(n)
b0
Forma trasposta II
x(n)
y(n)
z-1
z-1
-a1
b1
b1
b2
b2
-a2
z-1
z-1
-aM
-a1
z-1
z-1
-a2
y(n)
b0
bM
bM
-aM
z-1
z-1
-aN
-aN
25
Caso particolare: un filtro FIR
x(n)
z-1
b0
z-1
b1
z-1
z-1
b2
b3
bM
y(n)
forma diretta
x(n)
bM
bM-1
z-1
b2
z-1
b1
z-1
forma trasposta
26
b0
z-1
y(n)
Cascata di celle biquadratiche
M
H ( z) 
b
k 0
N
k
zk
bk 0  bk1 z 1  bk 2 z  2
  H k ( z)  
1
 ak 2 z  2
k 1
k 1 1  a k 1 z
K
1   ak z  k
bk 0  bk1 z 1  bk 2 z  2
H k ( z) 
1  a k 1 z 1  a k 2 z  2
K
k 1
poli e zeri complessi coniugati devono essere associati per ottenere i aki e bki reali
x(n) = x1(n)
H1(z)
y1(n) = x2(n)
x(n) b0
y(n)
z-1
H2(z)
y2(n)
xk(n)
x(n)
b0
z-1
b1
-a1
z-1
-a2
yk(n)
y(n)
xK(n)
x(n)
HK(z)
-a1
b1
z-1
-a1
z-1
b2
27
y(n)
z-1
b1
-a2
y(n)
b0
z-1
z-1
b2
Hk(z)
b2
-a2
Forma parallela
Ad esempio se H(z) ha N  M e poli siano tutti distinti (ipotesi non necessaria) si ha:
N

Ak
H ( z)  C 
1
1

p
z
k 1
k
i coefficienti pk sono i poli della funzione di trasferimento H(z)
i poli complessi coniugati devono essere associati in un’unica struttura a due poli.
x(n)
C
H1(z)
H2(z)
Hl(z)
HL(z)
y(n)
28
Effetti della lunghezza finita delle parole sui filtri digitali
differenze tra sistemi che utilizzano parole di lunghezza idealmente infinita e parole di
lunghezza finita per rappresentare
 i coefficienti
 i segnali
Quantizzazione dei coefficienti: la posizione dei poli e degli zeri del filtro varia
Sensitività della funzione di trasferimento alla quantizzazione dei coefficienti:
il generico filtro IIR caratterizzato dalla funzione di trasferimento
M
H ( z) 
 bk z
M
k
k 0
N
1   ak z  k
diventa
k 1
H ( z) 
k
b
z
 k
k 0
N
1  ak z k
k 1
dove i coefficienti ak e bk sono:
ak = ak + ak k = 1, 2, . . . , N
bk = bk + bk k = 1, 2, . . . , N
ak = errore di quantizzazione su ak
bk = errore di quantizzazione su bk
29
Esaminando i denominatori delle due funzioni di trasferimento:
N
N
k 1
k 1

D ( z )  1   a k z  k   1  p k z 1
pk = pk + pk k = 1, 2, . . . , N
p
pi   i ak
k 1 ak
N
pi

ak

N
N
k 1
k 1

D ( z )  1   a k z  k   1  p k z 1

pk = pk(a1, a2, a3, , ak))
 piN k
N
 ( pi  pl )
l 1
l i
 piN k
N
pi  
k 1
N
(p
i
 pl )
ak
l 1
l i
L’errore introdotto nella posizione dei poli può quindi aumentare, se si ha una coppia di
poli vicini, ben oltre quello che è l’errore di quantizzazione sui coefficienti.
Errore simile sugli zeri
Per minimizzare l’errore: realizzare ciascun polo e ciascuno zero in una sezione a
singolo polo e singolo zero. Problema: coefficienti complessi.
Meglio: celle biquadratiche, associando poli e zeri complessi coniugati (spesso
relativamente lontani nel piano z)
Il filtro rimane, anche se i coefficienti vengono quantizzati, un sistema lineare.
30
Esempio: quantizzazione dei coefficienti in un filtro FIR
FIR di ordine 24 equiripple ottimizzato a fase lineare, quantizzazione su 6 bit.
31
Modulo della funzione di trasferimento nel dominio delle frequenze analogiche,
supponendo una frequenza di ripetizione dei campioni pari a 40 MHz.
32
Quantizzazione e saturazione sui segnali
La quantizzazione trasforma il sistema in un sistema non lineare
x(n)
QLOUT
LIN
x(n)
LOUT
Effetti dell’arrotondamento su segnali non retroazionati
M
H ( z) 
b
k 0
N
k
z k
1   ak z k
K
  H k ( z)
k 1
k 1
x(n)
x(n)
x(n)
H(z)
y(n)
H1(z)
H2(z)
HK(z)
HK(z)
H1(z)
H2(z)
33
y(n)
y(n)
Con la quantizzazione:
x(n)
x(n)
x(n)
H1(z)
HK(z)
y1(n)
yK(n)
Q
Q
H(z)
y1(n)
yK(n)
y(n)
Q
y(n)
H2(z)
HK(z)
H1(z)
H2(z)
yQ1(n)
yQK(n)
Il quantizzatore diminuisce il rapporto segnale/rumore del sistema.
Stesso effetto se si riduce della lunghezza delle parole all’interno di un filtro, su segnali
che non subiscano retroazione.
Caratterizzazione della quantizzazione in termini statistici, in modo da mantenere il
modello del filtro lineare + errore di quantizzazione
34
Esempio: FIR del primo ordine
x(n)
x(n)
z-1
b0
b1
z-1
b0
b1
y(n)
y(n)
y(n) = Q[y(n)] = Q[b0x(n) + b1x(n-1)]
Q
y(n)
Q[.] = quantizzatore
Il sistema diventa non lineare: se il segnale di ingresso varia di una quantità abbastanza
piccola da non riuscire a modificare il bit meno significativo di y(n), o se non varia
affatto, non si ha nessuna differenza nel valore dell’uscita.
I sistemi in cascata si comporteranno di conseguenza.
Verifica: y(n) deve continuare ad es. a rappresentare il rapporto segnale/rumore espresso
da y(n) con una approssimazione sufficientemente alta, o comportare un effetto limitato
sulle prestazioni del sistema complessivo.
35
x(n)
x(n)
z-1
z-1
b0
b0
b1
Q
y(n)
Q
y(n)
b1
Q
y(n)
y(n) = Q[y(n)] = Q[b0x(n)] + Q[b1x(n-1)]
Per x(n) piccoli:
y(n) = Q[y(n)] = Q[b0x(n) + b1x(n-1)]
y(n)  0
Q[b0x(n)] = 0 e Q[b1x(n-1)] = 0
y(n) = 0
Strutture diverse con hardware diverso: da valutare!
Overflow e underflow su segnali non retroazionati
36
Oscillazioni in sistemi ricorsivi – Cicli limite
Spesso, in sistemi ricorsivi, la quantizzazione produce oscillazioni periodiche nell’uscita,
o un valore costante diverso da zero, anche se l’ingresso è a zero.
Esempio: IIR del primo ordine: y(n) = a y(n-1) + x(n) (stabile per |a| < 1)
x(n)
yid(n)
x(n)
rid(n)
yid(n)
rid(n)
z-1
z-1
a
a
H ( z) 
1
1  a z 1
x(n) espresso da parole a 5 bit modulo più segno rappresentazione frazionaria
x(n) = 0.x-1 x-2 x-3 x-4 corrisponde a x(n)10 = +(x-1 2-1 + x-2 2-2 + x-3 2-3 + x-4 2-4)
x(n) = 1.x-1 x-2 x-3 x-4 corrisponde a x(n)10 = - (x-1 2-1 + x-2 2-2 + x-3 2-3 + x-4 2-4)
yid(n) ha bisogno di infinite cifre per essere rappresentato
37
Quantizzazione del segnale di uscita yid(n)
yid(n) quantizzato su 5 cifre (4 modulo + segno), a = 1/2 su 5 cifre (0.1000)
x(n)
yid(n)
x(n)
rid(n)
yid(n)
Q
yid(n)
rid(n)
z-1
z-1
a
a
la parola viene arrotondata
n
x(n)
rid(n)
yid(n)
yid(n)
0
1
2
3
4
5
0.1000 0.0000
0.0000
0.0000
0.0000
0.0000
0.0000 0.01000000 0.00100000 0.00010000 0.00001000 0.00000100
0.1000 0.01000000 0.00100000 0.00010000 0.00001000 0.00000100
0.1000 0.0100
0.0010
0.0001
0.0001
0.0000
1/2
1/4
1/8
1/16
1/16
0
L’uscita nel sistema con quantizzazione va a 0, per il sistema ideale lo 0 è un limite (il
sistema è IIR)!
38
Quantizzazione del segnale di retroazione rid(n)
y(n) = Q[a y(n-1)] + x(n)
rQ(n) espresso su 5 bit
x(n)
y(n)
rQ(n)
z-1
Q
rid(n)
a
Il sistema il cui valore non raggiunge più il valore nullo, ma un valore continuo finito
n
x(n)
rQ(n)
y(n)
0
0.1000
0.0000
0.1000
1/2
1
0.0000
0.0100
0.0100
1/4
2
0.0000
0.0010
0.0010
1/8
39
3
0.0000
0.0001
0.0001
1/16
4
0.0000
0.0001
0.0001
1/16
5
0.0000
0.0001
0.0001
1/16
Caso ideale, a = 1.1000 (-1/2): l’uscita idealmente oscilla con ampiezza che diminuisce
n
x(n)
rid(n)
yid(n)
yid(n)
0
0.1000
0.0000
0.1000
0.1000
1/2
1
0.0000
1.01000000
1.01000000
1.0100
-1/4
2
0.0000
0.00100000
0.00100000
0.0010
1/8
3
0.0000
1.00010000
1.00010000
1.0001
-1/16
4
0.0000
0.00001000
0.00001000
0.0001
1/16
5
0.0000
1.00000100
1.00000100
0.0000
0
Caso con quantizzazione dopo la moltiplicazione, a = 1.1000 (-1/2): l’uscita oscilla
n
x(n)
rQ(n)
y(n)
0
0.1000
0.0000
0.1000
1/2
1
0.0000
1.0100
1.0100
-1/4
2
0.0000
0.0010
0.0010
1/8
3
0.0000
1.0001
1.0001
-1/16
40
4
0.0000
0.0001
0.0001
1/16
5
0.0000
1.0001
1.0001
-1/16
6
0.0000
0.0001
0.0001
+1/16
7
0.0000
1.0001
1.0001
-1/16
L’ampiezza dell’uscita in un ciclo limite (dead band) dipende dalle caratteristiche del
filtro e dal numero di bit con cui vengono arrotondate le operazioni
Quando un filtro a polo singolo si trova in un ciclo limite è di fatto un sistema non
lineare, ma si comporta come un sistema lineare con un polo zp = sign(a). Infatti:
 y (n  1)
Q[a y (n  1)]  
 y (n  1)
a0
a0
Poiché a y(n-1) è arrotondato (in modulo) su bQ bit, l’errore di quantizzazione deve
rispettare la disequazione:
1 b
Q[a y(n  1)]  a y(n  1)  2 Q
2

1 b
y(n  1)  a y(n  1)  2 Q
2
la dead band di un filtro a singolo polo è espressa da:
1 bQ
2
y (n  1)  2
1 a
41
Per un sistema a due poli i cicli limite sono molto più complessi.
Per un sistema identificato dall’equazione alle differenze:
y(n) = a1 y(n-1) + a2 y(n-2) + x(n)
Se i poli sono complessi coniugati l’ampiezza Aosc delle oscillazioni soddisfa:
Aosc
1 bQ
2
 2
1  a2
Il parametro a1 determina la frequenza delle oscillazioni.
E’ possibile anche avere dei cicli limite all’interno dei quali il sistema equivale ad un
sistema lineare con poli in z =  1. In questo caso:
b
Aosc
2 Q

1  a1  a 2
Se invece di arrotondare si tronca la parola in uscita al moltiplicatore molti dei cicli
limite (non tutti) scompaiono. Però è obbligatorio usare la rappresentazione modulo +
segno, per evitare polarizzazione dell’errore di troncamento, poco desiderabile
42
Sistema di ordine elevato parallelo di celle biquadratiche:
i cicli limite in uscita sono la somma di tutti i cicli limite delle singole celle.
Sistema di ordine elevato cascata di celle biquadratiche:
la situazione più complessa da analizzare: un ciclo limite originato da una cella
viene filtrato celle successive: può essere eliminato o enfatizzato (da evitare!)
Altri cicli limite: originati da overflow nella somma. Si può dimostrare che per un
sistema del secondo ordine, non si ha overflow se viene rispettata la condizione
|a1| + |a2| < 1 RESTRITTIVA!!!
Oppure: sommatore con saturazione (se la saturazione si verifica occasionalmente, la
distorsione da essa comportata può essere tollerata)
scaling del segnale di ingresso, in modo che nessun nodo interno saturi
(perdita della precisione con la quale x(n) è espresso, con conseguente
diminuzione del rapporto segnale/rumore in uscita).
43
Multirate Digital Signal Processing
Problema: cambiare la frequenza di elaborazione del segnale (sampling rate conversion)
D/A
Segnale digitale
a frequenza Fx
filtro
A/D
Fx
Segnale digitale
a frequenza Fy
Fy
Convertitore digitale
di frequenza
Segnale digitale
a frequenza Fx
Fx
x(n)
Fx = 1/Tx
Segnale digitale
a frequenza Fy
Fy
Filtro lineare
tempo variante
y(m)
Fy = 1/Ty
Fy
Fx

Tx I

Ty D
Decimazione: si diminuisce la frequenza di c elaborazione di un fattore intero D,
Interpolazione: si aumenta la frequenza di elaborazione di un fattore intero I.
44
Decimazione di un fattore D
x(n) segnale da sottocampionare; spettro X() con componenti nell’intervallo 0  ||  .
Non si può sottocampionare selezionando un campione di x(n) ogni D campioni (spettro
verrebbe replicato attorno alla frequenza Fx/2D)!
 prima si filtra x(n) con un filtro passa basso ideale con risposta in frequenza HD():
1
H D ( )  
0
  /D
altrove
la banda del segnale viene ridotta a MAX = /D (equivalente a FMAX = Fx/2D)
Si può sottocampionare! Nota: la decimazione non è tempo invariante!
x(n)
u(n)
hD(n)
Fx = 1/Tx

u ( n )   hD ( k ) x ( n  k )
k 0

Downsampler
D

y(m)
Fy = Fx/D
y (m)  u (mD)   hD (k ) x(mD  k )
k 0
45
Il sistema è tempo variante: non si possono utilizzare risposta in Z o risposta impulsiva.
Calcolo nel tempo: si definisca la sequenza û(n) = u(n) p(n):
u ( n)
uˆ ( n)  
0
u(n)
p(n)
û(n)
n  0,  D,  2D,
altrove
n
Esempio per D = 4
n
segnale
analogico
n
1 D 1 j 2kn / D
e
Rappresentazione mediante serie di Fourier discreta del segnale p(n): p(n) 
D k 0

Y ( z) 
y(m) = û(mD) = u(mD) p(mD) = u(mD)

 y ( m) z
m  
m


 uˆ (mD) z
m  
m


 uˆ(m) z
m  
(û(m) = 0 eccetto che per i multipli di D)
46
m / D
 1 D 1 j 2km / D   m / D 1 D 1
Y ( z )   u (m)   e
z
 

D k 0
m  
 D k 0


 
 u(m)e j 2k / D z1 / D 

m

m  

 

1 D 1
1 D 1
 j 2k / D 1 / D

Ue
z

H D e  j 2k / D z 1 / D X e  j 2k / D z 1 / D
D k 0
D k 0

( U(z) = Z(u(m)) = HD(z) X(z))
Spettro del segnale di uscita y(m): si valuta Y(z) per |z| = 1 in funzione della variabile y,
espressa in radianti relativamente alla frequenza di campionamento Fy:
y 
2F
 2FTy  2FDTx
Fy

 y  D x
L’intervallo 0  |x|  /D viene quindi a corrispondere con l’intervallo 0  |y|  .
 y   y  1
 y 
1 D1   y  2k    y  2k  1
 X 
  H D   X   
Y ( y )   H D 
X  
D k 0
D  
D  D

D D D D
(HD() è progettato in modo che le componenti che potrebbero dare origine all’aliasing
vengano eliminate, quindi tutti i termini si annullano, a parte il termine per k = 0)
47
x(n)
Fx = 1/Tx
Downsampler
D
u(n)
hD(n)
|X(x)|



x

|HD(x)|

D

x

D
|U(x)|

D

x

D
|Y(y)|



48
y
y(m)
Fy = Fx/D
Interpolazione per un fattore I
Si ”aggiungono” ad x(n) I-1 campioni in modo da mantenere le caratteristiche spettrali di
x(n).
m  0,  I ,  2I ,
altrove
 x(m / I )
u ( m)  
0
Upsampler
I
x(n)
Fx = 1/Tx
u(m)
aggiunti zeri
Fy = I Fx
U ( z) 

 u ( m) z
m  
m


 x ( m) z
 mI
 X (z I )
m  
Lo spettro di U(m) si ottiene calcolando il valore di U(z) sul cerchio di raggio unitario:
U ( y )  X ( y I )
y = 2 F/Fy = x / I (Fy = I Fx)
|X(x)|



Ripetizione di informazioni
Bisogna filtrare!
x
C  y   / I
H I ( y )  
0 altrove
|U(y)|

I
 
I

I

I

I
y = x /I
49
Upsampler
I
x(n)
Fx = 1/Tx
u(m)
hI(m)
Fy = I Fx
y(m)
Fy = I Fx
Lo spettro del segnale di uscita y(m) è quindi:
C X ( y I )
Y ( y )  
0
y   / I
C = fattore di scala in modo che
y(m) = x(m/I) per m = 0, I, 2I etc
altrove
Per m = 0:

 /I
1
C
y(0) 
Y
(

)
d


y
y
2 
2
I X ( y I )
Y ( y )  
0
C 1
X
(

I
)
d


y
y

I 2
 / I

 X ( x )d x 

y   / I
altrove
Come convoluzione:
y ( m) 


 h (m  k ) u(k )   h (m  kI ) x(k )
k  
I
k  
50
I
C
x(0)
I
Conversione della frequenza di campionamento per I/D razionale
Cascata di un interpolatore ed un decimatore
x(n)
Fx
Upsampler
I
hI(l)
I Fx
hD(l)
I Fx
I Fx
Downsampler
D
y(m)
Fy = I Fx/D
i due filtri passa basso operano alla stessa frequenza: possono essere sostituiti con un
unico filtro h(l) caratterizzato dalla risposta in frequenza H(u):
1 u  min(  / D,  / I )
H (u )  
0 altrove
x(n)
Fx
Upsampler
I
v(l)
u = 2F/Fu = 2F/IFx = x / I
u(l)
h(l)
I Fx
I Fx
Lo spettro della sequenza di uscita risulta essere:
 I  y
 X 
Y ( y )   D  D
0






 y  min   ,
altrove
51
D 

I 
Downsampler
D
y(m)
Fy = I Fx/D
Decimazione in più stadi
D
Se D >> 1 può essere fattorizzato nel prodotto di interi positivi:
allora:
x(n)
h1(n)
Fx
 D1
h2(n)
F1 =
Stadio 1
Fx
D1
 D2
Stadio 2
Banda passante del decimatore
Banda di trasizione del decimatore
F1
D2
D
j
j 1
hj(n)
F2 =
J
 Dj
Stadio J
y(m)
Fx
D
0  F  Fpc
Fpc  F  Fsc
(Fsc  Fx/2D)
l’aliasing nella banda 0  F  Fsc viene evitato scegliendo per ciascuno stadio:
Banda passante
Banda di transizione
0  F  Fpc
Fpc  F  Fi - Fsc
Banda di arresto
Fi - Fsc  F  (Fi-1)/2
ripple in banda per ciascuno stadio = ripple dell’intero filtro decimatore / # di stadi
La riduzione graduale della Fi permette di realizzare filtri con specifiche meno stringenti
rispetto al filtro passa basso necessario nel caso di decimazione in un unico stadio.
52
Strutture per il Multirate Digital Signal Processing
Strutture per la decimazione
La realizzazione più semplice: filtro FIR seguito dal decimatore:
x(n)
z-1
z-1
h(0)
h(1)
z-1
z-1
h(2)
z-1
h(M-1)
h(3)
h(M)
u(n)
Downsampler
D
Integrando il decimatore all’interno del filtro:
x(n)
D
h(0)
z-1
z-1
D
h(1)
z-1
D
h(2)
z-1
D
h(3)
z-1
D
h(M-1)
D
h(M)
y(m)
le moltiplicazioni e le somme vengono eseguite alla velocità Fy = Fx/D
53
y(m)
Per FIR a fase lineare simmetrico:
x(n)
z-1
z-1
D
x(n-M)
D
D
z-1
D
D
z-1
D
h(1)
z-1
D
z-1
D
h(0)
z-1
z-1
D
h(2)
z-1
D
h((M+1)/2)
h(3)
y(m)
54
Strutture per l’interpolazione
Un interpolatore inserisce I - 1 zeri tra i campioni del segnale x(n)
x(n)
1
u(n)
2
0
3
z-1
h(0)
z-1
z-1
h(1)
z-1
h(2)
z-1
h(M-1)
h(3)
h(M)
I
Upsampler
I
y(m)
x(n)
Upsampler
I
u(m)
h(M)
Forma trasposta
h(M-1)
h(2)
z-1
z-1
h(M)
h(M-1)
h(1)
z-1
h(0)
y(n)
z-1
x(n)
Inserimento dell’interpolatore
nel filtro
I
I
z-1
55
h(2)
h(1)
I
z-1
h(0)
I
z-1
I
z-1
y(n)
x(n)
z-1
z-1
D
z-1
D
h(0)
D
h(1)
z-1
D
h(2)
z-1
D
D
h(M-1)
h(3)
h(M)
y(m)
x(n)
h(M)
h(M-1)
I
h(2)
I
z-1
h(1)
I
z-1
I
z-1
56
h(0)
I
z-1
y(n)
57