Problemi di massimo e minimo
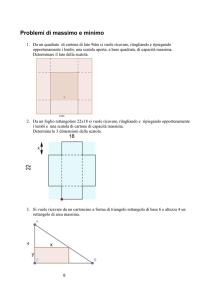
1. Da un quadrato di cartone di lato 9dm si vuole ricavare, ritagliando e ripiegando
opportunamente i lembi, una scatola aperta, a base quadrata, di capacità massima.
Determinare il lato della scatola.
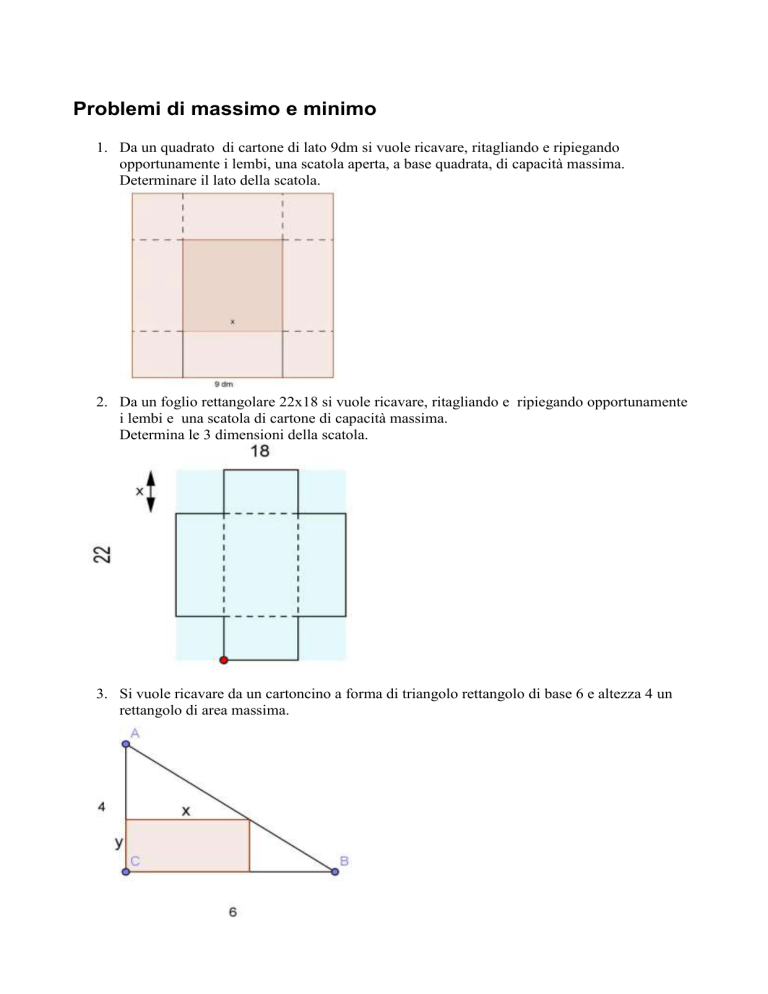
2. Da un foglio rettangolare 22x18 si vuole ricavare, ritagliando e ripiegando opportunamente
i lembi e una scatola di cartone di capacità massima.
Determina le 3 dimensioni della scatola.
3. Si vuole ricavare da un cartoncino a forma di triangolo rettangolo di base 6 e altezza 4 un
rettangolo di area massima.
4. A)Determina tra tutti i triangoli che hanno la somma dei cateti uguale a 6 quello di massima
area.
B)Determina tra tutti i triangoli che hanno la somma dei cateti costante quello di massima
area.
5. Il numero 10 deve essere diviso in 2 termini , in modo tale che la somma tra i loro quadrati
sia minima.
6. Determina tra tutti i rettangoli di area 10 quello di perimetro minimo.
7. Un lato di un campo da rettangolare è limitato da un ruscello; se si devono recintare gli altri
3 lati con una rete metallica lunga 1000m, quali devono essere le dimensioni del recinto
affinchè l'area sia massima.
8. Si deve costruire un campo da gioco avente la forma di un rettangolo più un'area
semicircolare a ciascun estremo. Il perimetro del campo deve essere lungo 400 m. Trovare le
dimensioni del campo se la parte rettangolare deve avere area massima possibile.
9. L'interno di un serbatoio della capacità di 32 litri (1litro =1dm3)senza coperchio e con il
fondo quadrato, deve essere rivestito di piombo con una lamina di dato spessore. Quali
devono essere le dimensioni affinchè la quantità di lamina da utilizare sia minima.
10. Fra tutti i parallelepipedi rettangoli di altezza 2 e superficie totale 24, determina quello di
volume massimo.
11. Un contenitore di liquidi di Volume V (1 dm³) che ha la forma di un parallelepipedo a base
quadrata. Quale deve essere la misura del lato di base e l’altezza del contenitore affinché la
superficie totale sia minima?
Quale deve la misura del raggio di base e l’altezza di un contenitore cilindrico di volume V
(250π cm³) affinché la superficie totale sia minima?
12. Rifai l’esercizio precedente nel caso in cui i contenitori sono aperti in alto.
13. All'interno di un mulino a forma di cono, avente altezza 2,5 m e base 3 m si vuole inserire
un contenitore d'acqua a forma cilindrica di raggio r e altezza h. Calcola il raggio e l'altezza
del contenitore di acqua che la massima capienza possibile.
( x CQ , y EQ , utilizza la similitudine tra 2 triangoli rettangoli)
14. Ad una lastra di vetro nel formato A4 (297 mm x 210 mm) è stato tagliato un angolo a 50
mm nel lato più corto e a 70 mm nel lato più lungo.
Con la parte di vetro rimanente bisogna ritagliare una lastra rettangolare di dimensioni
massime possibili.
(Consiglio: utilizza la similitudine tra 2 triangoli rettangoli, chiama xAHEJ, trova in
funzione di x DJ poi FK ed infine i 2 lati HO e DH .
15. Il triangolo rettangolo ABC ha l'ipotenusa AB=14 e l'angolo CÂB= π/3.
Si descriva internamente al triangolo, con centro in B e raggio x, l'arco di circonferenza di
estremi P e Q rispettivamente su AB e BC. Sia poi R l'intersezione con il cateto CA dell'arco
di circonferenza di centro A e raggio AP. Si esprima in funzione di x l'area S del
quadrilatero mistilineo PQCR e si trovi quale sia il valore minimo e quale il valore massimo
di S(x).
16. Inscrivere in una sfera di raggio R =12 dm il cilindro con la superficie laterale maggiore.
17. Inscrivere nel segmento parabolico, delimitato dall’asse x e dalla parabola di equazione
y=4x-x2 il rettangolo di perimetro massimo.
18. A)Tra tutti i coni che hanno apotema 6, determina quello di volume massimo. (Determina il
raggio x e altezza di tale cono)
B)Tra tutti i coni che hanno apotema a, determina quello di volume massimo. (Determina il
raggio x e altezza di tale cono)
19. Un ragazzo che si trova in un punto A, situato lungo un rettilineo di una strada di campagna,
deve raggiungere la propria ragazza che si trova (ad aspettarlo ansiosamente) in un casolare
situato in un punto B, distante 8 km dalla strada, in mezzo ad un prato. La distanza in linea
d'aria tra A e B è di 17 km. Il ragazzo può correre a 5 km/h sulla strada e a 3 km/h sull'erba
del prato. In quale punto dovrà abbandonare la strada se, come è naturale, vuole raggiungere
la propria ragazza nel più breve tempo possibile?
20. Di tutti i rettangoli inscritti in un medesimo cerchio di raggio 8 , qual è quello di perimetro
massimo?
21. Un furgone deve percorrere 600 km su una strada alla velocità costante di x km/h. I limiti di
velocità impongono che la velocità minima sia di 60 km/h, e quella massima di 120km/h.
x2
10
Si supponga che le benzina costi 1,300 euro al litro (!!) e che si consumino
litri
600
all'ora. Se la paga dell'autista è di 10 euro all'ora, si chiede qual è la velocità che rende
minimo il costo del viaggio nell'ipotesi che l'autista rispetti i limiti di velocità.