Ottobre 2010

IEEE News Ottobre 2010
Elettronica da indossare grazie al grafene e ai memristori
Le due tecnologie più innovative degli ultimi 5 anni preparano la strada ad una nuova elettronica, quella da
“indossare”. Annunciati nel 2008, i memristori (ne abbiamo parlato su questa rubrica) possono realizzare
memorie ad alta densità, economiche e a basso consumo. Usando strati all’ossido di grafene, si possono
realizzare circuiti elettronici facili da fabbricare su rotoli di plastica, che si possono addirittura indossare
come abiti. Ricercatori nella Corea del Sud hanno appunto realizzato memorie non volatili a base di
memristori, all’ossido di grafene. Ricordiamo che i memristori hanno una resistenza che cambia in base alla
tensione e al suo verso, ma anche sono in grado di memorizzare il livello logico senza la tensione, si
comportano cioè, per certi versi, come transistor. L’idea del memristore risale al 1971 ma solo oggi HP ha
presentato dispositivi pronti per la commercializzazione, entro i prossimo 3 anni. D’altra parte il transistor
fu concepito 100 anni fa, realizzato da ricercatori Francesi della tedesca Telefunken durante la seconda
guerra mondiale, e commercializzato a partire dagli anni ’50 del novecento. Il memristore HP usa due
matrici di collegamenti separati da uno strato di biossido di titanio. Ogni elemento perpendicolare allo
strato di titanio ossidato è un memristore. Sembra che silicio, grafene e titanio siano gli elementi tuttofare
della moderna tecnologia.
Il grafene, il materiale
ecologico per l’elettronica del futuro
Il memristore coreano è simile a quello di HP, ma usa l’ossido di grafene al posto del titanio. I collegamenti
sono di alluminio e misurano 50 micro, su un quadrato di plastica di 6,5 cm di lato stanno 25 memristori.
Come si vede le dimensioni sono enormi rispetto agli integrati convenzionale ed anche rispetto ai
memristori HP, ma qui lo scopo è dimostrativo e i memristori coreani costano pochissimo. Il memristore
può commutare 100000 volte, un valore pari alle memorie Flash di oggi. Fra poco si passerà a un milione di
commutazioni.
I robot umanoidi coreani all’assalto degli Asimo giapponesi
Il Giappone vanta il predominio nei robot umanoidi e più o meno tutti hanno visto Asimo, un robot alto
come un bambino che cammina, sale le scale, corre. Ora i ricercatori della Corea del Sud hanno presentato
un robot umanoide alto come un uomo e dotato di grande agilità. La competizione è aperta.
Ruote omnidirezionali per la robotica
Le ruote omnidirezionali, capaci di andare in ogni direzione, sono una recente invenzione e trovano impiego
naturale nella robotica industriale. Oggi si possono trovare anche in kit per robot educativi di costo
inferiore a 500 euro offerti, ad esempio, dalla ditta americana Parallax.
Due ruote omnidirezionali
Soluzione del quesito matematico
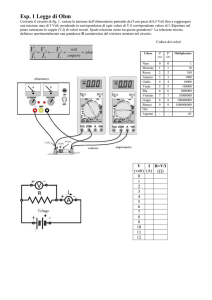
Il problema proposto nelle ICT news di ottobre era questo:
il computer (o un amico) sceglie un numero intero a caso fra 1 e 1000 e propone di indovinarlo. Ad ogni
vostro tentativo risponde con ‘maggiore’, ‘minore’, esatto. Dopo quanti tentativi, usando la migliore
strategia di gioco, siete sicuri di indovinare ?
Avevamo accennato che la strategia migliore da adottare è analoga a quella usata in un circuito elettronico
che si chiama convertitore A/D (analogico – digitale) ad approssimazioni successive. Vediamo come
funziona. Supponiamo di avere una tensione analogica in ingresso di da 0 a 10 Volt da convertire in un
numero digitale in uscita di 8 bit, da 0 a 255 in decimale.
27
26
25
24
23
22
21
20
128
64
32
16
8
4
2
1
Il convertitore è detto ad approssimazioni successive perché procede a determinare, in passi successivi, i bit
dal più significativo (a sinistra) al meno significativo (destra). Si comincia generando una tensione analogica
di metà del fondo scala, cioè 5 Volt, corrispondente al valore digitale 1000 0000 (128 decimale). Questa
tensione è confrontata con quella da convertire. Supponiamo che sia 6 Volt. Se il confronto dà maggiore o
uguale (come in questo caso), il primo bit (quello più significativo) è 1. A questo punto, il primo intervallo di
tensione, da 0 a 5 Volt viene scartato e si divide a metà il secondo, da 5 a 10 Volt. Viene generata una
tensione di 7,5 Volt, corrispondente a 1100 0000. Si effettua il secondo confronto che dà esito minore. Il
secondo bit è 0. L’uscita (parziale) è dunque
10.. ….
Si procede così in 8 passi fino all’ultimo bit. I passi sono sempre 8, qualunque sia la tensione da convertire.
Adesso torniamo al giochino del numero da indovinare. E’ chiaro che la strategia di gioco migliore è quella
che sfrutta al massimo l’informazione che ci viene fornita dopo ogni tentativo: maggiore – minore – esatto.
All’inizio abbiamo 1000 possibili numeri, da 1 a 1000. Ma dopo il primo tentativo, se proponiamo 500,
scartiamo la metà delle possibilità: se ci viene risposto ‘maggiore’, scartiamo tutti i numeri da 1 a 500,
altrimenti da 500 a 1000. Supponiamo che il numero casuale da indovinare sia 437 e ci venga detto
‘minore’, si capisce bene che ora ci conviene provare con metà di 500, cioè 250. La risposta al secondo
tentativo è ‘maggiore’ e proponiamo perciò 375 (250 + 125). Esattamente con 10 tentativi abbiamo la
certezza di indovinare, qualunque fosse il numero generato a caso. Dimostriamolo. Ad ogni risposta
scartiamo metà dei numeri: 500, 250, 125… fino a 1; dividiamo perciò per 2. E’ più comodo ragionare a
ritroso, ‘riavvolgendo’ quello che facciamo. Partiamo da 1 (2 elevato a 0) e moltiplichiamo ogni volta per 2:
1, 2, 4, 8, 16…, fino a raggiungere 512 e infine 1024. A questo punto basta. Quante volte dobbiamo
moltiplicare ? La risposta è 10: 210. Se ci ricordiamo i logaritmi, il numero di tentativi è il più piccolo intero
maggiore o uguale al logaritmo in base 2 di N, se N è il numero più grande, nel nostro caso 1000. I logaritmi
crescono molto meno del numero al quale sono applicati. Se, ad esempio dobbiamo indovinare un numero
da 1 a 1 milione, quindi, abbiamo 1000 volte più possibilità, ma ci bastano 20 tentativi ! La strategia che
abbiamo usato, nota anche come ricerca binaria o dicotomica, è assai nota ed usatissima nelle applicazioni
informatiche.
Il gioco del numero da indovinare è analogo ai ben noti quiz televisivi come il gioco del numero di fagioli in
un vaso, proposto anni fa da Raffaella Carrà. Ben presto i telespettatori scoprirono la strategia ottima che
abbiamo qui descritto, e il gioco fu modificato perché durava troppo poco: non si rispondeva più ‘maggiore’
– ‘minore’, ma solo giusto o sbagliato. In questo caso la strategia migliore per indovinare un numero a caso
è di generarne, da parte nostra, un altro a caso, di rispondere cioè al caso col caso.
Un’ultima considerazione. I numeri del gioco del lotto sono puramente casuali: l’urna non ha memoria.
Dunque la strategia di gioco migliore non è certo affidarsi ai ‘numerologi’ delle TV, coi loro ‘ritardatari,
vertibili, gemelli’ e simili amenità. Il modo migliore è giocare numeri generati caso. Ma il gioco del lotto è
anche un gioco iniquo: la Stato paga meno di quello che corrisponde alla ‘speranza matematica’ di vincere:
è naturale, lo Stato deve guadagnare. In Italia, il gioco del lotto fu introdotto dal mitico ministro delle
Finanze biellese Quintino Sella, ingegnere e scienziato, dopo che aveva imposto ogni genere di tasse, per
portare in pareggio il bilancio statale, disastrato dalle guerre di indipendenza. Lo chiamava appunto “La
tassa sui babbei”.
Quintino Sella