Chiave pubblica e privata - Prima parte - Classi Perlo

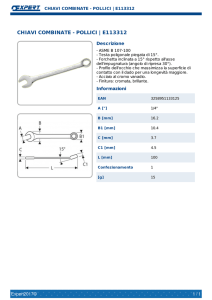
INFORMATICA – ESERCITAZIONE DI LABORATORIO
CHIAVE PUBBLICA E PRIVATA – 1
Autori: _______________________________________________
Data: _______________________________________________________________
ATTENZIONE: Se hai scaricato questa esercitazione nelle lezioni scorse e non hai ancora
cominciato a compilarla, prima di iniziare scaricala di nuovo da Classiperlo e butta via questa
versione, perché nel frattempo potrebbe essere stata modificata. Se invece avevi già cominciato
l’esercitazione, ignora questo messaggio.
Tutte le immagini copiate e incollate in questa esercitazione devono essere protette da watermark.
Le immagini prive di watermark (col numero del PC su cui si lavora) non verranno accettate.
A) OPERAZIONI PRELIMINARI
All’interno del disco di rete, nella vostra cartella personale o di gruppo, create una sottocartella di
nome Informatica.
Dentro la cartella Informatica\Esercitazioni, create una sottocartella Es13A (la lettera A indica che
si tratta della prima parte dell’esercitazione 13).
All’interno della sottocartella Es13A salvate questo file Word e compilate l’intestazione.
B) UN PO’ DI TEORIA (SOLO DA LEGGERE)
Come abbiamo ormai visto in numerosi esempi, un sistema di cifratura si basa su:


un algoritmo o metodo di cifratura
una chiave di cifratura
La sicurezza del sistema si basa ovviamente sulla sicurezza di entrambi gli elementi, cioè sul
fatto di disporre di un buon algoritmo di cifratura e di una buona chiave.
Un problema generale è quello della condivisione della chiave fra mittente e destinatario e
questa difficoltà diventa ancora maggiore al crescere della lunghezza della chiave usata. Infatti
in che modo mittente e destinatario possono scambiarsi la chiave di cifratura/decifratura?
Qualsiasi canale di comunicazione usato (per telefono, per lettera, per email, via radio, con un
incontro di persona, etc.) presenta problemi di sicurezza e la possibilità che la chiave venga
intercettata da qualcuno.
Il problema è che la chiave non può essere a sua volta cifrata, poiché in tal caso bisognerebbe
preventivamente accordarsi sulla chiave di cifratura e così via all'infinito. In pratica, mittente e
destinatario devono scambiarsi la chiave di cifratura prima di iniziare la corrispondenza e per
fare questo devono usare un metodo non cifrato. Per esempio, nel caso semplice del cifrario di
Cesare, Giulio Cesare potrebbe comunicare a voce la chiave ai propri generali oppure potrebbe
inviargliela per mezzo di un messaggero fidato, ma in entrambi i casi la chiave potrebbe essere
intercettata da una spia nemica.
Il problema della condivisione delle chiavi è forse la debolezza principale dei sistemi
crittografici tradizionali. Questo problema viene superato soltanto con i sistemi di cifratura
moderna, i quali non richiedono due chiavi separate (per crittare e decrittare il messaggio) e
non richiedono lo scambio della chiave di decifratura.
In generale dunque si distingue fra:

crittografia simmetrica: la funzione di codifica e quella di decodifica usano la stessa
chiave, o chiavi diverse ma in diretta relazione tra loro (derivazione).

crittografia asimmetrica: si usano due differenti chiavi, una per crittare il messaggio
e un'altra per decrittarlo.
B1) Vediamo se state seguendo il mio ragionamento. Tutti gli esempi di algoritmi di
cifratura che abbiamo visto finora, a quale delle due categorie precedenti appartengono?
C) UN ESEMPIO PRATICO DI CRITTOGRAFIA ASIMMETRICA (RSA)
In crittografia la sigla RSA indica un algoritmo di crittografia asimmetrica, inventato nel 1977 da
Ronald Rivest, Adi Shamir e Leonard Adleman utilizzabile per cifrare o firmare informazioni
(l’acronimo RSA deriva appunto dalle iniziali dei cognomi dei tre inventori).
Il sistema di crittografia si basa sull'esistenza di due chiavi distinte, che vengono usate per cifrare e
decifrare. Se la prima chiave viene usata per la cifratura, la seconda deve necessariamente essere
utilizzata per la decifratura e viceversa. La questione fondamentale è che nonostante le due chiavi
siano fra loro dipendenti, non è possibile risalire dall'una all'altra, in modo che se anche si è a
conoscenza di una delle due chiavi, non si può risalire all'altra, garantendo in questo modo
l'integrità della crittografia.
Supponiamo di chiamarci Bob e che Alice ci voglia mandare una mail con la ricetta del suo famoso
Tiramisù (per qualche strana ragione, in tutti gli esempi di crittografia i due protagonisti si
chiamano sempre Bob e Alice). Siccome si tratta di una ricetta segretissima, Alice teme che possa
cadere nelle mani di sua madre che cerca sempre di rubarle le ricette. Decidiamo allora con Alice di
crittografare la mail con la ricetta, in modo tale che nessun altro possa leggerla.
Per fare questo dobbiamo metterci d’accordo su due cose:
1) un algoritmo di cifratura
2) una chiave di cifratura
Per quanto riguarda il punto 1) non ci sono problemi: come abbiamo visto c’è una grande
abbondanza di algoritmi di cifratura disponibili e, volendo andare sul sicuro, potremmo sceglierne
uno dei più moderni (es. AES), in modo tale che, anche se la mamma di Alice dovesse disporre di
un supercomputer modernissimo, non sarà mai in grado di craccare il nostro messaggio.
C1) Con quale tipo attacco, disponendo di un supercomputer, la mamma di Alice
potrebbe cercare di decrittare il messaggio? E perché, se scegliamo bene il metodo, i suoi tentativi
sono destinati a fallire? Scrivete qui le vostre idee:
Per quanto riguarda la scelta dell’algoritmo, possiamo metterci d’accordo tranquillamente con Alice
per telefono o via mail, senza nessun timore di eventuali intercettazioni.
C2) Perché siamo così tranquilli e non abbiamo paura di eventuali intercettazioni?
Attenzione, questo è un punto importante. Fra algoritmo e chiave, cosa è davvero indispensabile
mantenere segretissimo?
Il problema maggiore è rappresentato dalla chiave di cifratura. Infatti, supponendo che Bob abbia
scelto il sistema di cifratura che andrà a utilizzare, come può egli comunicare la chiave ad Alice?
Per telefono? Via mail? Qualunque sistema decidiamo di usare, se la chiave cade in mani nemiche,
siamo fritti!
Qui ci viene in aiuto la crittografia asimmetrica RSA. La prima cosa che devo fare è generare una
coppia di chiavi di cifratura.
C3) Collegatevi con questo sito http://travistidwell.com/jsencrypt/demo/ , scegliete la
lunghezza desiderata delle chiavi (per il nostro esempio 512 bit possono andare bene, anche se
attualmente questo valore non è considerato sicuro) e generate due chiavi, una Privata e l’altra
Pubblica. Copiate qui i valori delle due chiavi (compresa la parte di testo all’inizio e alla fine):
C4) Perché il valore 512 come lunghezza della chiave attualmente non è considerato
sicuro? Spiegate:
Ora che disponiamo di due chiavi, procediamo nel seguente modo: la chiave Privata di Bob la
teniamo segreta e nascosta in un cassetto (o nel PC di Bob); la chiave Pubblica invece la
comunichiamo ad Alice via mail (o per telefono, se non abbiamo problemi di bolletta!). Volendo
Bob potrebbe anche pubblicare la sua chiave Pubblica sull’elenco telefonico, su un giornale oppure
scriverla su uno striscione appeso alla sua finestra. Insomma la chiave Pubblica può davvero essere
resa pubblica (se volete potete anche andare in giro con una macchina e un megafono e urlare la
vostra chiave pubblica a tutti: occhio però che se vi prendono vi portano dritti al manicomio).
Anche se la mamma di Alice è in ascolto, nascosta da qualche parte, la chiave Pubblica non le serve
proprio a niente, per le ragioni che vedremo fra un attimo.
C5) Facciamo ora un esperimento per vedere come funziona il metodo. Scrivete qui una
breve ricetta a vostra scelta (potete anche inventare, basta che sia breve!):
C6) Ora mettiamoci nei panni di Alice che vuole spedire la ricetta a Bob. Usando la
pagina http://www.classiperlo.altervista.org/File%20comuni/RSA/rsa.html e USANDO LA
CHIAVE PUBBLICA scelta al punto C3 crittografiamolo. Scrivete qui sotto il testo della ricetta
crittografata con la nostra chiave Pubblica:
Notate che Alice ha usato la chiave Pubblica di Bob per crittografare il testo. Ma lei e nessun altro
(e soprattutto non la mamma di Alice) conoscono la nostra segretissima chiave Privata. Che
conseguenze ha questo fatto?
C7) Chi è l’unica persona al mondo che è in grado di leggere la ricetta crittata del famoso
Tiramisù di Alice? Lo so che è una domanda difficile, ma ce la potete fare a rispondere…
C8) E adesso viene il bello. Bob riceve la ricetta segreta di Alice. Quale chiave dovrà
usare per riuscire a leggerla? Lo so che lo sapete, ma scrivetemelo qui…
C9) E ora provate a decrittare la vostra ricetta segreta sempre usando la pagina
http://www.classiperlo.altervista.org/File%20comuni/RSA/rsa.html Se avete scelto la chiave giusta,
dovreste riuscire a leggere il testo in chiaro della vostra ricetta. Copiate qui sotto una schermata
(protetta da watermark) in cui si veda il testo decrittato:
Ok, ragazzi, finora abbiamo giocato. Adesso le cose si fanno serie. Ecco il testo crittato del vero,
originale famoso Tiramisù di Alice:
Rnrqj9LGGPM5BA9qDl7z2qDL0yNeSnGiO1cXh6QGpH/XMLrJQl0g3OPtbvBLyKzn+2b/HyBm
LUmSxX/FLFbSzlfsgCgwPsfNUffSSlOpJtaXSemfn5inBMnYlvpdhENryk2dV0TOHX6kS+8auq/q
eFHz5Kaa87DWhkksJZ28MF8=
E qui sotto avete la vera coppia di chiavi, Pubblica e Privata, di Bob:
-----BEGIN PUBLIC KEY----MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCpU8kNN8OPxW1M2eQwIOvG0kB6
DqVEHnNwjdL40un+1MIkgxjau4wjKr5a9h3k9X9MOmTUmZ3+N4HDJod3RgJqyIgP
PV+irKiW74CGlj3Iu2FnCntNFz/nYR1rGUmVhuDBg/9hXN8j7C40o8biET4Ri+4Q
8HXL552CdSF68VFBcwIDAQAB
-----END PUBLIC KEY---------BEGIN RSA PRIVATE KEY----MIICXAIBAAKBgQCpU8kNN8OPxW1M2eQwIOvG0kB6DqVEHnNwjdL40un+1MIkgxja
u4wjKr5a9h3k9X9MOmTUmZ3+N4HDJod3RgJqyIgPPV+irKiW74CGlj3Iu2FnCntN
Fz/nYR1rGUmVhuDBg/9hXN8j7C40o8biET4Ri+4Q8HXL552CdSF68VFBcwIDAQAB
AoGAOC1bA66fjCB1Dc0wfqM9dh4lVBltzTbJF+uFthXLmkceDh0Mbu1QJg61Ttpe
uqqUTEcHUt2QZFooDAXJZdHtVNGjpkkY2C3BrHahGutZ0VU9d+nF+bh9tOiitw8X
t201uVJyNt758GYnHIqNo1apiAnj3PQHCx6k7o2WzVp8kpECQQD6gdRbGIm35W0G
X4M9i9jB3OdRJr3xkwKSvRu7zEddMPZmpcF/0fp/CHchrn90gQXePui8K8zHUShn
Z0/2OTSrAkEArQpE9B0YwrmZyGEIeXoJ42uYZjIydR7iTlnomtWLbF9QATRDGz5Q
Pmws5K0RPUDtu4IHjncl1KZ6iyB72jXWWQJBAJJQHj4OuPFl2SXtx3O9KJ8ibSDi
5fIhEVGvjnFDwTLXFDOkAL6tYAeuZBaSGvNrIIhMahbt5i9MYbLzjqqbgv0CQHJE
HsaI1En6H/f3Q45cLV11Npz9tt4qd8y/iF9+dmQpCH7TESFTY8/kxTx4oLKvRo2U
zwKf4WZsTO3ElKTC+nkCQEc58yyxrw55E6ZCZ3e9bSoe4NyvuNCwBtIaLU/PaMJL
XHRWFj+MUwGehYXLEJXfnZ780FsnEktYIFqGF0IqcG0=
-----END RSA PRIVATE KEY---
C10) E ora tocca a voi. Scegliendo la chiave giusta (ricordatevi che voi siete Bob e state
ricevendo un messaggio crittografato da Alice) decrittate il messaggio e copiate qui sotto una
schermata con la ricetta di questo famoso Tiramisù:
Se avete capito tutto questo, fatevi subito i complimenti da soli (anche da parte mia). Questi sono
argomenti che si solito si spiegano all’università (non sto scherzando), perché ritenuti troppo
difficili. Eppure voi ci siete arrivati, giusto? Dunque, prima di proseguire, complimentatevi!
Per essere proprio sicuri di aver capito tutto, ora supponiamo di metterci nei panni di Bob e di voler
rispondere ad Alice ringraziandola per la ricetta. Non vogliamo però che il messaggio venga
intercettato dalla mamma di Bob (che è una grande pettegola) e a tale scopo decidiamo di
crittografarlo usando RSA.
C11) A questo punto dovreste dirmi:
1) quale chiave deve usare Bob per crittografare il messaggio:
2) quale chiave usa Alice per leggerlo:
Per rispondere alle domande precedenti potete usare qualsiasi combinazione di parole, come per
esempio “Bob cifra con la chiave Privata di Bob e Alice decifra con la chiave Pubblica di Bob” (è
sbagliato, ovviamente, ma vi serve come modello di esempio).
Attenzione: tutta la difficoltà nel comprendere bene questo meccanismo sta nel fare confusione sul
tipo di chiave (Pubblica o Privata) e su chi le ha generate (Bob o Alice).
C12) A proposito, nel nostro ultimo esempio, chi ha generato le chiavi usate? Bob o
Alice?
D) COME VENGONO GENERATE LE CHIAVI DI CIFRATURA
La chiave Privata e quella Pubblica sono generate insieme da un algoritmo che, sebbene non sia
eccessivamente complicato, sarebbe troppo lungo da spiegare qui. Il punto da capire è che
l’algoritmo di generazione della coppia di chiavi si basa su una coppia di numeri primi, che
attraverso una serie di passaggi matematici si trasformano nei valori delle due chiavi. Pubblica e
Privata.
D1) Vi ricordate qual è la definizione di numero primo? Scrivetela qui:
Lo schema in figura mostra simbolicamente il passaggio dalla coppia di numeri primi alle due
chiavi di cifratura:
I due numeri primi da cui parte tutto il calcolo possono essere scelti da chi vuole generare la coppia
di chiavi oppure generati più o meno casualmente da un programma per computer. Il punto è che
più questi due numeri sono grandi, più sicura è la coppia di chiavi.
Ma prima di cercare di capire un po’ meglio questi dettagli, vediamo la generazione di una coppia
di chiavi di cifratura all’opera.
Per prima cosa dovete scegliere due numeri primi, P e Q da cui partire. Di solito, come abbiamo
detto, si usano numeri primi molto grandi per questi calcoli, ma noi possiamo fare un esempio con
numeri più piccoli.
D2) Per aiutarvi nella scelta collegatevi col sito
https://primes.utm.edu/lists/small/1000.txt dove sono elencati i primi 1000 numeri primi.
Sceglietene due che vi stanno simpatici (non troppo piccoli) e scriveteli qui:
D3) Collegatevi col sito
https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html e copiate i numeri primi
che avete scelto nelle caselle P e Q. Quindi premete il bottone Set p,q. Copiate qui sotto una
schermata dove si veda il risultato (casella di testo Candidates):
D4) Ora dalla lista Candidates (1 mod r) dovete scegliere, più o meno a caso, uno dei
numeri proposti. Scrivete qui il numero che avete scelto:
Copiate il numero scelto nella casella K e premete il bottone Factor K. Il programma vi scompone
automaticamente il numero K scelto in un prodotto di numeri primi. Se i fattori primi sono più di
due, scartate il numero e provate con un altro nella lista, magari più piccolo. Continuate a provare
finché non trovate un K fra quelli elencati che ha solo due fattori primi.
D5) Copiate qui sotto una schermata dove si veda il numero K e la sua fattorizzazione in
numeri primi:
Adesso copiate i due fattori primi di K nelle caselle e e d. Premete il bottone Check e & d. Se non
avete fatto errori dovrebbe comparirvi le scritte:
e*d mod r = 1
e and r are relatively prime
d and r are relatively prime
D6) Se non succede, chiamate l’insegnante. Altrimenti copiate qui sotto una schermata
con i valori di e e di d che avete scelto:
Adesso finalmente siamo arrivati alla fase di cifratura. Nella casella Msg dovete inserire un
messaggio in forma numerica. In pratica bisogna usare il codice ASCII.
D7) Codificate la parola ROMA in ASCII e scrivete qui i relativi codici (decimali):
D8) Ora scrivete i codici tutti attaccati (senza spazi) in Msg e premete Encode/Decode. Se
non avete fatto errori, nella casella Encrypted dovrebbe comparire il vostro messaggio cifrato con la
chiave pubblica che avete appena generato. Copiate qui sotto una schermata dove si veda il numero
corrispondente:
Scopo di tutto questo giochino è farvi toccare con mano il fatto che alla base della crittografia RSA
c’è una coppia di numeri primi, i quali, con una serie di calcoli più o meno incomprensibili,
generano le chiavi di cifratura.
Ma perché proprio due numeri primi? E perché questi due numeri devono essere molto grandi?
Volete la spiegazione lunga e difficile o quella breve o veloce? Ok, ho capito…
In breve i numeri primi hanno una proprietà che li rende interessantissimi per la crittografia. I fatti
sono questi: è facilissimo moltiplicare fra loro due numeri primi, ma è molto complicato prendere il
prodotto di due numeri primi e scomporlo nei due fattori.
D9) Non ci credete? Prendete due numeri primi, per esempio 19 e 31 e moltiplicateli fra
loro. Potete usare la calcolatrice. Scrivete qui il risultato:
Quanto ci avete impiegato? Poco, non è vero? Ora proviamo a vedere l’inverso…
D10) Il numero 893 è il prodotto di due numeri primi. Quali sono? Uhm, vi comincia a
fumare il cervello? Riuscite a vedere la difficoltà di scomporre un numero nei suoi fattori primi?
In pratica l’unico sistema sensato che i matematici sono riusciti a inventare in secoli e secoli di
studio è… fare tutte le prove. Ebbene sì. Per scomporre un prodotto nei fattori primi che lo hanno
formato, l’unico sistema è prendere una lista di numeri primi e provare a dividere. Bello, vero? E
soprattutto molto veloce…
Cosa c’entra questo con la crittografia? Bene, vi ricordate che all’inizio del nostro ultimo esercizio
vi ho chiesto di scegliere due numeri primi per generare le chiavi Pubblica e Privata? Bene, uno dei
passaggi matematici fondamentali nel calcolo delle chiavi è il prodotto fra questi due numeri primi
che avete scelto. Date un’occhiata alla pagina
https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html (non l’avete chiusa, vero?)
e vedrete che c’è una casella indicata con N = p * q:
In effetti una parte della chiave pubblica è proprio formata da N, cioè dal prodotto dei due numeri
primi scelti all’inizio. Ora, se un ipotetico assalitore volesse risalire dalla chiave pubblica a quella
privata, l’unico modo sensato (a parte l’approccio a forza bruta, che consiste nel provare tutte le
chiavi) è quello di provare a calcolare i due numeri p e q che hanno dato inizio a tutto il gioco,
partendo dalla conoscenza del loro prodotto N.
E’ come cercare di scomporre 893 nei suoi due fattori primi… solo che in questo caso i numeri sono
molto più grossi!
Questo calcolo è difficilissimo, ci siamo? Detto in modo ancora più semplice: per creare la coppia
di chiavi si prendono due numeri primi, li si mescola fra di loro in vari modi, si aggiunge un po’ di
sale e pepe e una spruzzata di prezzemolo per insaporire e il risultato sono due belle chiavi di
cifratura (nelle quali si trova il prodotto fra i due numeri primi di partenza).
Se un attaccante volesse risalire dal prodotto N ai numeri p e q che lo hanno generati (e dunque
ricostruirsi le due chiavi a proprio uso e consumo), avrebbe enormi difficoltà. E’ un po’ come voler
estrarre dalla maionese le uova… è facile mescolarle, difficile separarle di nuovo!
La moltiplicazione fra due numeri primi è un’operazione banale che è difficilissima da invertire. E’
un lucchetto facile da chiudere (basta moltiplicare due numeri) e difficile da aprire. Ci siamo?
La cattiva notizia per i cifratori è che i computer diventano sempre più potenti e veloci ogni anno
che passa e compiti che fino a ieri sembravano impossibili, oggi sono alla portata anche del vostro
smartphone. Anche la fattorizzazione in fattori primi non è un problema insormontabile, se i numeri
scelti non sono davvero giganteschi.
D11) Collegatevi col sito http://www.mathwarehouse.com/arithmetic/numbers/primenumber/prime-factorization-calculator.php e calcolate la fattorizzazione del numero 893 che ci
aveva messo in crisi un minuto fa. Qual è?
D12) Proviamo con qualcosa di più cattivo. Trovate i fattori primi di 1581255209. Fatto?
Scriveteli qui…
Come vedete anche numeri che sembrano molto grandi, sono scomponibili in fattori primi in un
tempo velocissimo con i moderni computer. Per questa ragione i numeri usati per generare le chiavi
di cifratura sono davvero enormi (si parla di migliaia di bit, cioè numeri così grandi che è
impossibile quasi scriverli). Per adesso nessuno è ancora riuscito a fattorizzarli (e dunque a
indovinare le chiavi), ma domani… chissà!
E) INVIARE L’ESERCITAZIONE ALL’INSEGNANTE
Creare una cartella compressa col contenuto dell’esercitazione (ES13A) e inviarla all’insegnante su
classiperlo. Prima di inviare l’esercitazione, chiedere all’insegnante di verificare che tutti gli
esercizi siano stati svolti correttamente (ATTENZIONE: inviate tutta la cartella compressa, non
solo questo file con le spiegazioni!).