N.37
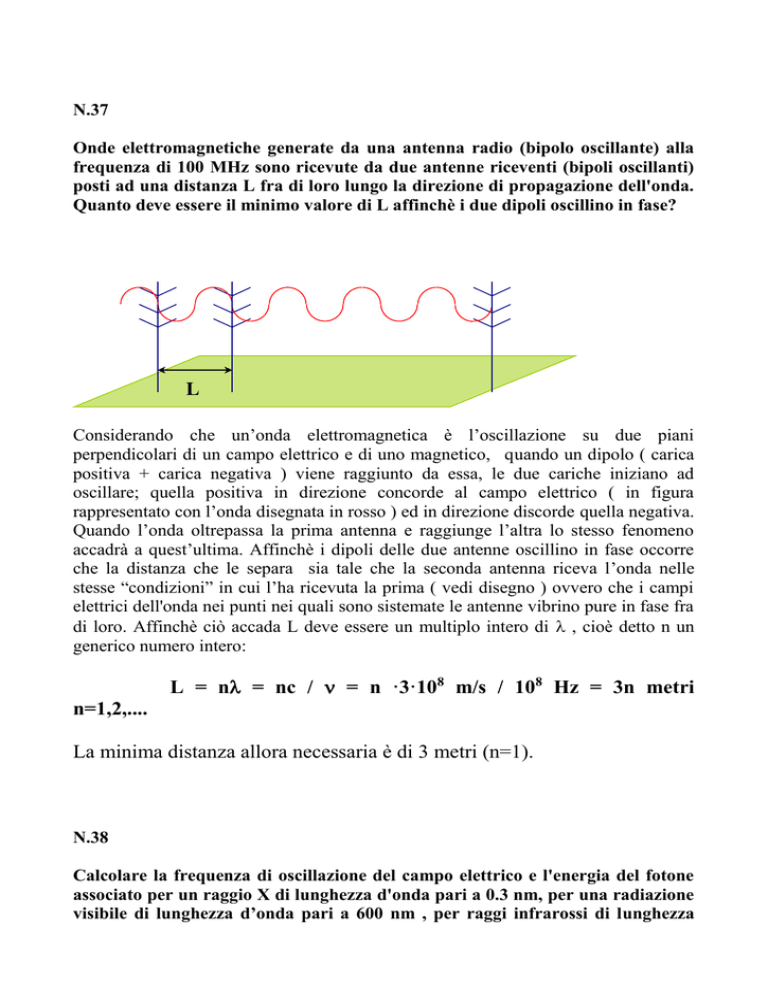
Onde elettromagnetiche generate da una antenna radio (bipolo oscillante) alla
frequenza di 100 MHz sono ricevute da due antenne riceventi (bipoli oscillanti)
posti ad una distanza L fra di loro lungo la direzione di propagazione dell'onda.
Quanto deve essere il minimo valore di L affinchè i due dipoli oscillino in fase?
L
Considerando che un’onda elettromagnetica è l’oscillazione su due piani
perpendicolari di un campo elettrico e di uno magnetico, quando un dipolo ( carica
positiva + carica negativa ) viene raggiunto da essa, le due cariche iniziano ad
oscillare; quella positiva in direzione concorde al campo elettrico ( in figura
rappresentato con l’onda disegnata in rosso ) ed in direzione discorde quella negativa.
Quando l’onda oltrepassa la prima antenna e raggiunge l’altra lo stesso fenomeno
accadrà a quest’ultima. Affinchè i dipoli delle due antenne oscillino in fase occorre
che la distanza che le separa sia tale che la seconda antenna riceva l’onda nelle
stesse “condizioni” in cui l’ha ricevuta la prima ( vedi disegno ) ovvero che i campi
elettrici dell'onda nei punti nei quali sono sistemate le antenne vibrino pure in fase fra
di loro. Affinchè ciò accada L deve essere un multiplo intero di , cioè detto n un
generico numero intero:
L = n = nc / = n ·3·108 m/s / 108 Hz = 3n metri
n=1,2,....
La minima distanza allora necessaria è di 3 metri (n=1).
N.38
Calcolare la frequenza di oscillazione del campo elettrico e l'energia del fotone
associato per un raggio X di lunghezza d'onda pari a 0.3 nm, per una radiazione
visibile di lunghezza d’onda pari a 600 nm , per raggi infrarossi di lunghezza
d'onda pari a 30 μm, per microonde con lunghezza d'onda pari a 3 cm e per
onde radio con lunghezza d'onda pari a 3 Km. Riportare i valori ottenuti in
funzione della lunghezza d'onda in un grafico in scala logaritmica.
1 Angstrom, Ǻ 1 nm
1 micron, μ
1 cm
1 metro
1 Km
RAGGI GAMMA ULTRAVIOLETTO INFRAROSSO
ONDE
RADIO
RAGGI X
LUCE VISIBILE
MICROONDE
Nel grafico qui sopra riportato troviamo le varie denominazioni delle onde
elettromagnetiche in funzione della loro lunghezza d’onda. Tra la lunghezza d’onda e
la frequenza dell’onda elettromagnetica ( che è anche la frequenza con cui oscillano il
campo elettrico e quello magnetico ) sussiste la seguente relazione:
ν=c/λ
Nota la frequenza ν , l’energia del fotone associato all’onda elettromagnetica vale:
E = hν
dove h è la costante di Planck.
RAGGI X
3 108 m / s 3 108 m / s
18
10
Hz
10
0.3nm
3 10 m
c
E h 6.626 1034 J s 1018 s 1 6.626 1016 J
RADIAZIONE VISIBILE
3 108 m / s 3 108 m / s
0.5 1015 Hz 5 1014 Hz
7
600nm
3 2 10 m
c
E h 6.626 10 34 J s 5 1014 s 1 3.313 10 18 J
RAGGI INFRAROSSI
3 108 m / s 3 108 m / s
1013 Hz
5
30 m
3 10 m
c
E h 6.626 1034 J s 1013 s 1 6.626 1021 J
MICROONDE
3 108 m / s 3 108 m / s
10
10
Hz
3cm
3 10 2 m
c
E h 6.626 10 34 J s 1010 s 1 6.626 10 24 J
ONDE RADIO
3 108 m / s 3 108 m / s
5
10
Hz
3
3Km
3 10 m
E h 6.626 10 34 J s 105 s 1 6.626 10 29 J
c
Grafichiamo ora i dati ottenuti, come richiesto, in scala logaritmica (
graficheremo quindi sulle ascisse il logaritmo della lunghezza d’onda e sulle
ordinate il logaritmo della frequenza ):
1,00E+19
1,00E+18
1,00E+17
Frequenza ( Hz )
1,00E+16
1,00E+15
1,00E+14
1,00E+13
1,00E+12
1,00E+11
1,00E+10
1,00E+09
1,00E+08
1,00E+07
1,00E+06
1,00E+05
1,00E+04
1,00E-11
1,00E-09
1,00E-07
1,00E-05
1,00E-03
1,00E-01
1,00E+01
1,00E+03
1,00E+05
Lunghezza d'onda ( m )
Cerchiamo di capire come mai la curva che unisce i nostri punti è una retta.
Sappiamo che la relazione che lega la lunghezza d’onda λ e la frequenza ν è:
ν=c/λ
Facciamo il logaritmo ( in base 10 ) di entrambi i membri:
Log ν = Log (c / λ) = Log c Log λ
Facendo le seguenti posizioni:
y = Log ν
x = Log λ
e ricordando che, essendo c una costante, anche Log c è una costante, allora
possiamo scrivere:
y = cost x
in cui riconosciamo l’equazione di una retta con pendenza negativa e coefficiente
angolare 1 , come abbiamo anche ottenuto nel nostro grafico.
N.39
Un vetro colorato ha un assorbimento elevato per la radiazione e.m. di
lunghezza d’onda compresa fra 500 e 800 nm e basso per la rimanente parte
dello spettro della luce visibile. Di che colore apparirà in trasparenza?
BLU
4∙107m
ROSSO
LUCE
8∙107m VISIBILE
Come si può vedere dal grafico su riportato la luce visibile contiene lunghezze d’onda
comprese tra circa 400 nm e circa 800 nm.
Se il vetro ha un alto assorbimento tra 500 nm e 800 nm, se guardiamo il vetro in
trasparenza le lunghezze d’onda comprese in queste intervallo saranno assorbite e
non arriveranno al nostro occhio, dove invece arriveranno le lunghezze d’onda
comprese tra 400 nm e 500 nm, che vengono assorbite molto di meno per come ci
dice il problema. In questa zona dello spettro la luce è di colore blu, quindi vedremo
il vetro blu.
N.40
Luce polarizzata incide su una lamina polaroide con la direzione del
campo elettrico a 0, 30, 45, 60 e 90 gradi rispetto la direzione di
polarizzazione del polarizzatore. Calcolare i rapporti fra le intensità
della luce emergente nei vari casi rispetto l'intensità di quella
emergente nel caso di 0°.
La luce , che ricordiamo è un’onda elettromagnetica, consiste come tutte le onde
elettromagnetiche, di un campo elettrico e di uno magnetico variabili ma di direzione
mutuamente perpendicolare, come nella seguente figura:
Nonostante tutto però la direzione del campo elettrico ( e quindi anche quella del
campo magnetico ) non è sempre fissa, ma può anche variare sia pur restando sempre
in un piano ortogonale alla direzione di propagazione. In questo caso la luce si dice
non polarizzata . Un polaroide consiste di un materiale in grado di propagare la luce,
quando questa lo attraversa, solo in una direzione , caratteristica del polaroide
chiamata direzione di polarizzazione. Se luce non polarizzata passa attraverso un
polaroide, quest’ultimo selezionerà solo la componente del campo elettrico parallela
al suo asse di polarizzazione, e oltre il polaroide ( cioè dopo che la luce lo ha
attraversato ) troveremo luce polarizzata lungo l’asse di polarizzazione del polaroide.
La situazione può essere schematizzata così:
Se ora però facciamo passare questa luce ora polarizzata attraverso un secondo
polaroide, l’intensità della luce emergente dal secondo polaroide risulterà:
I = I0 cos² θ
dove I0 è l’intensità della luce prima di attraversare il secondo polaroide e θ è
l’angolo tra la direzione di polarizzazione del primo e del secondo polarizzatore.
Questa legge è detta legge di Malus. Uno schema di quanto detto può essere
riassunto nella seguente figura:
Il problema ci propone la situazione in figura rappresentata nel quadrato in rosso.
Applichiamo la legge di Malus nel caso che l’angolo tra la direzione di
polarizzazione della luce e l’asse di trasmissione del polarizzatore sia 0°, 30°, 45°,
60°, 90°:
I ( 0°) = I0 cos² 0° = I0
I ( 30°) = I0 cos² 30°= I0 ( ¾ ) = ¾ I0
I ( 45°) = I0 cos² 45° = I0 ( ½ ) = ½ I0
I ( 60°) = I0 cos² 60° = I0 ( ¼ ) = ¼ I0
I ( 90° ) = I0 cos² 90° = 0
Poichè il problema richiede l’intensità rispetto a quella a 0°, calcoliamo:
I ( 0°) / I ( 0°) = 1
I ( 30°) / I ( 0°) = ¾
I ( 45°) / I ( 0°) = ½
I ( 60°) / I ( 0°) = ¼
I ( 90°) / I ( 0°) = 0
N.41
Calcolare la separazione angolare fra i massimi di interferenza da due
fenditure distanti d per luce di lunghezza d’onda 5000 Ǻ assumendo
d= l mm, d = 0.1 mm e d = 10 μm.
Sappiamo che, date due fenditure distanti d , i massimi di interferenza che si
ottengono su uno schermo posto davanti alle fenditure , soddisfano la relazione:
d·sen θ = m λ
dove θ è l’angolo ( in radianti ) a cui si osserva l’interferenza costruttiva ( quindi il
massimo ) , λ è la lunghezza d’onda della radiazione elettromagnetica che passa
attraverso le fenditure e di cui si osserva l’interfenza ed m è l’ordine del massimo.
Nel nostro caso supporremo , come accade nella maggior parte dei casi , che l’angolo
sia piccolo per cui vale la relazione:
sen θ ≈ θ
per cui possiamo scrivere per due massimi di ordine m1 ed m2
d·θ1 = m1 λ
d·θ2 = m2 λ
cioè
θ1 = (m1 λ)/d
θ2 = (m2 λ)/d
sottraendo membro a membro, otteniamo la separazione angolare:
θ1 θ2 = ( m1 m2 )·( λ / d )
supponendo di prendere due massimi successivi, quindi che valga m1 m2 = 1
otteniamo:
θ1 θ2 = λ / d
quindi
per d=1 mm
per d=0.1 mm
per d=10 μm
θ1 θ2 = 5000·1010 m / 103 m = 5·104
radianti
=0,029°
θ1 θ2 = 5000·1010 m / 104 m = 5·103 radianti
=0,29°
θ1 θ2 = 5000·1010 m / 105 m = 0.05
radianti =2,9°
N.42
Una lamina vetrosa osservata con luce bianca perpendicolarmente alla
superficie appare di colore blu, un’altra di colore verde. Sapendo che
per entrambe le lamine si osservano massimi interferenziali del primo
ordine dire quale delle due lamine è più spessa.
Il fenomeno dell’interferenza della luce accade anche all’interno di lamine sottili
dove, se l’indice di rifrazione della lamina è n, la lunghezza d’onda della luce
all’interno della lamina è data da:
λn = λ / n
(1)
dove λ è la lunghezza d’onda della luce nel vuoto. Le condizioni di interferenza
costruttiva si possono esprimere nel seguente modo:
2t = ( m + ½ ) λn
(2)
dove t è lo spessore della lamina ed m è l’ordine del massimo. Quando questa
relazione è soddisfatta le onde riflesse dalle due facce della lamina sono in fase e
quindi interferiscono costruttivamente. Dalla (1) e (2):
2nt = ( m + ½ ) λ
Il problema ci dice che nelle due lamine dobbiamo considerare il massimo di ordine
uno , cioè dobbiamo porre m = 1
2nt = 3/2 λ
λ = 4/3nt
cioè la lunghezza d’onda della luce riflessa (e che aumenta la sua intensità a causa di
una interferenza costruttiva fra le onde riflesse dalle due superfici) cresce con lo
spessore della lamina; ciò ci suggerisce che la lamina più spessa riflette una
lunghezza d’onda maggiore; ora poichè il verde ha una lunghezza d’onda maggiore
del blu la lamina più spessa è quella che riflette il verde, quella più sottile riflette il
blu.
sostituendo il λ ottenuto dalla relazione precedente otteniamo:
d sen θ2 = 2·d sen 15°
quindi
sen θ2 = 2 sen 15°
θ2 31°












