Area dei poligoni

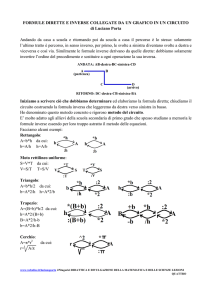
Area dei
poligoni
quadrato
rettangolo
triangolo
parallelogrammo
trapezio
rombo
esagono regolare
Le ultime parole famose…
GEOMETRIA?
Questa presentazione
è inutile per me! Nessuno è
mai riuscito a farmi
entrare NIENTE in testa,
figuriamoci la geometria!
Torna alle formule
Le ultime parole famose…
Torna alle formule
Il quadrato
magico
Area del quadrato
A  l l
Al
lato
2
l A
lato
Torna alle formule
Ma un quadrato è “magico”
se una fata ha fatto un
incantesimo?
Area del rettangolo
h
b
A  bh
Questa storia di misurare
la base e poi l’altezza non
mi quadra, anzi, non mi
“RETTANGOLA”!
Torna alle formule
Rettangolo: formule inverse
Se la formula inversa è
“LAVORO” quella diretta
dovrebbe essere “RIPOSO”!
A  bh
A
b
h
A  bh
A
h
b
Diretta sì,inversa
no, diretta sì,
inversa no, diretta
sì, inversa no…
Torna alle formule
Area del triangolo
Lo zio mi ha detto di cercare di “essere alla sua
ALTEZZA”. Proverò ad indossare la sua giacca.
Non si sa mai! Potrei già essere alto quanto lui…
h
b
bh
A
2
Torna alle formule
Triangolo: formule inverse
bh
A
2
2 A
b
h
Basta! Non puoi fare coppia con me!
Sei la mia brutta copia! Il mio
contrario, la mia “formula inversa”!
bh
A
2
2 A
h
Torna alle formule
b
Area del parallelogrammo
A  bh
h
b
Il problema dà la base e l’altezza e vuole l’area… Dunque, vediamo un po’.
Devo stare calmo e riflettere… Altezza, base, area… è davvero un rompicapo.
Allora, concentriamoci, ricapitolando: con base e altezza si deve trovare
l’area… è davvero molto, molto complesso. Sono a cena da Paperina, ma devo
assolutamente riuscire a risolvere il problema entro stasera!
Torna alle formule
Area del parallelogrammo
h1
b1
A  bh
1
1
Nessuno osi interrompermi! Sto componendo! Mi manca
solo … l’ultima formula!
Torna alle formule
Area del parallelogrammo
h1
b1
h2
A  bh
2
2
b2
Urrà! Ho risolto correttamente il problema
di geometria! Che genio! Che portento! Da
Torna alle formule
grande mi daranno il premio NOBEL…
Oscurerò Einstein e anche Newton, ma
soprattutto… LISA!
Parallelogrammo: formule inverse
A  bh
A
b
h
A
h
b
Ho chiesto alla maestra di dirmi
il risultato del problema ma lei
non
ha
voluto
dirmelo
rispondendomi che uno come me,
può anche stare sulla “CORDA”!
Torna alle formule
I trapezi
Mi hanno detto che camminare
risolve molti … PROBLEMI. Per
questo passeggio molto: spero di
imparare a risolvere tutti i
problemi di … geometria.
I trapezi sono quadrilateri aventi due
lati
opposti
paralleli,
detti
base
maggiore B e base minore b. Possono
essere isosceli rettangoli e scaleni.
Io già li
conosco!
Un trapezio si dice isoscele se
ha i due lati obliqui uguali.
Trapezio
isoscele.
Un trapezio si dice rettangolo se
ha uno dei due lati obliqui
perpendicolare alle basi.
Trapezio
rettangolo
.
Un trapezio si dice scaleno se ha i due lati
obliqui disuguali.
Scaleno
Area del trapezio
Concerto per
“TRAPEZISTI”
Eccomi! Nessuno è più
“TRAPEZISTA” di me!
Torna alle formule
Trapezio: formule inverse
A=
h=
2A
(B+b)
2A
B=
b
(B + b) h
2
h
=
2A
h
- b
- B
Eccomi! Col mondo tra le mani saprò
risolvere ogni tipo di PROBLEMA!
Torna alle formule
Area del rombo
Ho un problema
col rombo!
Non so proprio
come cucinarlo!
D
d
Dd
A
2
Torna alle formule
Area dell’esagono regolare
Rombo: formule inverse
Dd
A
2
2 A
D
d
È vero che sono il più intelligente, ma non possono pretendere
che sia sempre io a risolvere tutti i loro problemi!
Dd
A
2
2 A
d
D
Torna alle formule
Poligoni regolari
a = h
apotema  altezza
l
h
3
2
Li chiamano poligoni
REGOLARI ma
secondo me in
geometria è tutto …
IRREGOLARE!
Torna alle formule
Apotema e lato nei
poligoni regolari
a  l  nf
a
l 
nf
Torna alle formule

l  6 a
A
Area dell’esagono regolare
3
A  6
2
l a
12
A  3l  a
A  pa
apotema  altezza
l
l
A  p
3
ah
3
2
2
Chissà se c’è
un genio che
ci capisce
qualcosa!
l
A  3l 
3
2
A  l 2 1,5  3
3 1,732
a
lato
A  l  2,598
2
costante k esagono
2,598
Torna alle formule
Area dell’esagono regolare
Al K
2
Torna alle formule
Esagono: formule inverse
2pa
A
2
2 A
 2p
a
Urrà! Mi sembra un
sogno! Sono riuscito
ad imparare tutte le
formule dell’esagono!
2pa
A
2
2 A
a
2p
Torna alle formule
Una giornata problematica
Camminavo in una piazza QUADRATA
quando nella vetrina RETTANGOLARE di
un negozio, in una piazza
TRIANGOLARE, ho visto una cornice a
forma di PARALLELOGRAMMO con
decorazioni TRAPEZIODALI. C’era anche
un quadretto ROMBOIDALE con piccoli
ESAGONI. Non avendo soldi in tasca, mi
sono accorto di avere un PROBLEMA e
allora l’ho RISOLTO tornandomene a
casa. Tutta quella GEOMETRIA non
faceva per me e così ho trovato la
giusta SOLUZIONE!
CIAO a tutti!