Le Leggi Fisiche
La descrizione delle proprietà e dei comportamenti del
mondo fisico è contenuta in alcune affermazioni chiamate.
LEGGI FISICHE
Una legge fisica in pratica è LA RELAZIONE
MATEMATICA (FORMULA) CHE INTERCORRE TRA LE
GRANDEZZE FISICHE IN GIOCO.
Per ricavare una legge fisica occorre seguire il metodo
scientifico (introdotto da Galileo Galilei) composto dai
seguenti punti:
osservazione preliminare del fenomeno
individuazione delle grandezze fisiche che descrivono il
fenomeno
formulazione di un’ipotesi, cioè di una relazione che lega fra loro
le grandezze fisiche in gioco
ideazione e realizzazione di esperimenti che possono verificare
concretamente l’ipotesi teorica
se la teoria e’ confermata dalla pratica (esperimento) si può
formulare la legge fisica che descrive il fenomeno considerato.
Le relazioni tra due grandezze fisiche (che possiamo
chiamare genericamente x e y), utilizzate per descrivere un
fenomeno, si possono esprimere mediante l’uso di tabelle,
in cui si raccolgono i valori che le grandezze assumono,
mediante grafici e per mezzo di
funzioni matematiche (formule).
Ovviamente c’è una relazione tra questi tre modi di
rappresentazione; ad esempio i dati raccolti in una tabella
possono essere trasformati in un grafico; utilizzando una
formula è possibile costruire una tabella; e così via.
RAPPRESENTAZIONE DATI
SPERIMENTALI
Il metodo più semplice ed immediato per
rappresentare dei dati sperimentali consiste
nell’utilizzare un grafico cartesiano.
Per costruire un grafico cartesiano si procede nel
seguente modo:
si disegnano due assi perpendicolari (assi cartesiani), uno orizzontale
(asse delle ascisse) ed uno verticale (asse delle ordinate); il punto in
cui si incontrano e’ detto ORIGINE degli assi cartesiani.
si orientano gli assi (aggiungendo una freccetta in fondo agli assi) e
vicino a ciascun asse si scrive il simbolo della variabile rappresentata.
Chiamiamo VARIABILI le grandezze che compaiono nel
grafico o nelle tabelle o nelle funzioni.
Si dicono variabili perché possono assumere valori di volta
in volta diversi.
Solitamente le variabili considerate sono due e sono
chiamate rispettivamente VARIABILE INDIPENDENTE e
VARIABILE DIPENDENTE.
A partire dai valori assunti dalla variabile indipendente, si
ricavano i valori corrispondenti della variabile
dipendente.
In matematica si scrive y = f(x); questa espressione si può
leggere indifferentemente:
la variabile y è funzione della variabile x;
y dipende da x;
x e’ la variabile INDIPENDENTE e y è la variabile
DIPENDENTE;
al variare del valore x, ne consegue un valore di y.
In pratica, in fisica, si può pensare alla variabile
indipendente come CAUSA e alla variabile dipendente
come EFFETTO.
RICORDIAMOCI UNA REGOLA: nei grafici, sull’asse
delle ascisse si deve sempre indicare la VARIABILE
INDIPENDENTE, mentre sull’asse delle ordinate si
deve sempre indicare la VARIABILE DIPENDENTE.
PROPORZIONALITA’ DIRETTA
La più semplice relazione tra grandezze fisiche e’ la
relazione di PROPORZIONALITA’ DIRETTA.
Costruiamo una tabella per esprimere la relazione tra
due variabili x e y.
X
Y
0
0
1
4
2
8
3
12
4
16
5
20
Si può vedere che quando la variabile x raddoppia, anche la
variabile y raddoppia, quando x triplica, anche y triplica, etc.
Quindi, se facciamo il rapporto y/x si può notare che questo
rapporto e’ costante ed in questo caso vale 4.
y
k = ── = 4
x
Quando il rapporto tra due grandezze è costante si dice che
le due grandezze sono DIRETTAMENTE PROPORZIONALI.
Due grandezze si dicono DIRETTAMENTE
PROPORZIONALI quando il loro RAPPORTO è
COSTANTE.
y
── = k
x
Questa relazione si può esprimere anche come:
y=kx
N.B.: Rappresentando le due grandezze su di
un grafico cartesiano otteniamo una retta
passante per l’origine.
Viceversa, se su un grafico è rappresentata una
retta passante per l’origine, significa che le due
grandezze rappresentate sono
DIRETTAMENTE PROPORZIONALI.
y
0
x
L’inclinazione della retta rispetto all’asse X è detta
PENDENZA (possiamo approssimativamente indicarla
con l’angolo α) e dipende dal valore della costante k.
Più è grande il valore di k, maggiore è l’angolo che la
retta forma con l’asse X.
Se la pendenza è maggiore, significa che la grandezza rappresentata dalla variabile
dipendente (y) varia più rapidamente. Nella figura sottostante l’angolo β risulta > α,
per cui la retta rossa ha una pendenza maggiore della retta verde e quindi la
grandezza rappresentata dalla retta rossa varia più rapidamente dell’altra.
y
β
α
0
x
Altre relazioni matematiche
Se la retta NON passa per l’origine, la relazione tra le
due grandezze e’ detta LINEARE.
dove a e b rappresentano dei valori costanti.
Costruiamo una tabella per esprimere la relazione tra
due variabili.
Prendiamo un recipiente già parzialmente pieno e
aggiungiamo acqua in modo costante. In questo caso la
quantità d’acqua V nel recipiente e il tempo t sono
grandezze correlate linearmente.
T (min)
V (litri)
0
3
1
5
2
7
3
9
4
11
In questo caso si vede che il rapporto tra y e x NON e’ costante;
la relazione tra x e y e’ espressa dalla formula:
y=k∙x+q
q praticamente rappresenta il punto in cui la retta attraversa
l’asse y (e per questo in matematica e’ detta ORDINATA
ALL’ORIGINE).
Nel nostro esempio si vede che y = 2x + 3 e quindi k = 2 e q = 3
(la nostra retta attraversa l’asse y nel punto di ordinata = 3).
PROPORZIONALITA’ INVERSA
Un’altra relazione tra due grandezze e’ la
PROPORZIONALITA’ INVERSA.
Costruiamo una tabella per esprimere la relazione tra
due variabili x e y
X
Y
10
600
20
500
30
400
40
300
50
200
60
100
Si può vedere che quando la variabile x raddoppia, la
variabile y dimezza, quando x triplica, y diventa 1/3, etc.
Quindi se facciamo il prodotto y ∙ x, si può notare che
questo prodotto e’ costante.
Nel nostro esempio il prodotto tra x e y e’ sempre = 6000.
y ∙ x = k = 6000
Quando il prodotto tra due grandezze e’ costante, si dice
che le due grandezze sono INVERSAMENTE
PROPORZIONALI.
Quindi due grandezze si dicono INVERSAMENTE
PROPORZIONALI quando il loro PRODOTTO e’
COSTANTE.
y∙x=k
N.B.: Se rappresentiamo le due grandezze su di un grafico
cartesiano otteniamo un ramo di iperbole.
Viceversa, se su un grafico e’ rappresentato un ramo di
iperbole, significa che le due grandezze rappresentate sono
INVERSAMENTE PROPORZIONALI.
PROPORZIONALITA’ QUADRATICA
L’ultima relazione che prendiamo in considerazione e’
la PROPORZIONALITA’ QUADRATICA.
Costruiamo una tabella per esprimere la relazione
tra due variabili x e y dove x e y rappresentano
rispettivamente il raggio e l’area di un cerchio.
L’area e il raggio di un cerchio sono legate da
proporzionalità quadratica. Al raddoppiare del
raggio l’area diventa 4 volte più grande, al triplicare
del raggio l’area diventa 9 volte più grande ….
dove a rappresenta una costante.
Quindi una grandezza y si dice che ha una proporzionalità
quadratica rispetto ad una grandezza x, quando, dividendo i
valori che assume la y per i corrispondenti valori di x al quadrato,
si ottiene sempre lo stesso valore k:
y
── = k
x2
oppure
y = k ∙ x2
Se rappresentiamo le due grandezze su di un grafico
cartesiano otteniamo una parabola.
Viceversa, se su un grafico e’ rappresentata una
parabola, significa che fra le due grandezze
rappresentate esiste una proporzionalità
quadratica.
RIASSUMENDO
Due grandezze x e y sono direttamente
proporzionali quando il loro rapporto e’ costante;
la formula che esprime la relazione di proporzionalità
diretta è
y
── = k
x
Il grafico di y in funzione di x è una retta passante
per l’origine degli assi.
Due grandezze sono legate dalla relazione lineare
quando
y=k∙x+q
Il grafico di y in funzione di x e’ una retta NON
passante dall’origine degli assi, ma dal punto q (per
questo q si chiama anche ORDINATA ALL’ORIGINE).
Due grandezze x e y sono inversamente
proporzionali quando il loro prodotto e’ costante;
la formula che esprime la relazione di proporzionalità
inversa e’
y∙x=k
Il grafico di y in funzione di x e’ un ramo di iperbole.
La proporzionalità quadratica e’ espressa dalla
relazione matematica
y
── = k
x2
Il grafico che esprime la relazione tra x e y e’ una
parabola.
Le Leggi Fisiche
La descrizione delle proprietà e dei comportamenti del
mondo fisico è contenuta in alcune affermazioni
chiamate……….
LEGGI FISICHE
Una legge fisica in pratica è LA RELAZIONE
MATEMATICA (FORMULA) CHE INTERCORRE TRA LE
GRANDEZZE FISICHE IN GIOCO.
Per ricavare una legge fisica occorre seguire il metodo
scientifico (introdotto da Galileo Galilei) composto dai
seguenti punti:
osservazione preliminare del fenomeno
individuazione delle grandezze fisiche che descrivono il
fenomeno
formulazione di un’ipotesi, cioè di una relazione che lega fra loro
le grandezze fisiche in gioco
ideazione e realizzazione di esperimenti che possono verificare
concretamente l’ipotesi teorica
se la teoria e’ confermata dalla pratica (esperimento) si può
formulare la legge fisica che descrive il fenomeno considerato.
Le relazioni tra due grandezze fisiche (che possiamo
chiamare genericamente x e y), utilizzate per
descrivere un fenomeno, si possono esprimere
mediante l’uso di tabelle, in cui si raccolgono i valori
che le grandezze assumono, mediante grafici e per
mezzo di funzioni matematiche (formule).
Ovviamente c’è una relazione tra questi tre modi di
rappresentazione; ad esempio i dati raccolti in una
tabella possono essere trasformati in un grafico;
utilizzando una formula è possibile costruire una
tabella; e così via.
RAPPRESENTAZIONE DATI
SPERIMENTALI
Il metodo più semplice ed immediato per
rappresentare dei dati sperimentali consiste
nell’utilizzare un grafico cartesiano.
Per costruire un grafico cartesiano si procede nel
seguente modo:
si disegnano due assi perpendicolari ……………
(assi cartesiani),
uno orizzontale ………………………..
(asse delle ascisse)
ed uno verticale …………………………
(asse delle ordinate);
il punto in cui si incontrano e’ detto ……………………
ORIGINE degli assi cartesiani.
si orientano gli assi (aggiungendo una freccetta in fondo agli assi) e vicino a ciascun asse
si scrive il simbolo della variabile rappresentata.
Le grandezze che compaiono nel grafico o nelle tabelle o nelle
funzioni sono dette ………..........
VARIABILI
Si dicono variabili perché possono assumere valori di volta in
volta diversi.
Solitamente le variabili considerate sono due e sono chiamate
rispettivamente …………………..
VARIABILE INDIPENDENTE e VARIABILE DIPENDENTE.
A partire dai valori assunti dalla variabile indipendente, si
ricavano i valori corrispondenti della variabile dipendente.
In matematica si scrive ………………
y = f(x);
questa espressione si può leggere indifferentemente:
la variabile y è funzione della variabile x;
y dipende da x;
x e’ la variabile …………………
INDIPENDENTE
e y è la variabile ……………………
DIPENDENTE;
al variare del valore x, ne consegue un valore di y.
In pratica, in fisica, si può pensare alla variabile
indipendente come …………….
CAUSA
e alla variabile dipendente come ………………..
EFFETTO.
RICORDIAMOCI UNA REGOLA: nei grafici, sull’asse
delle ascisse si deve sempre indicare la VARIABILE
INDIPENDENTE, mentre sull’asse delle ordinate si
deve sempre indicare la VARIABILE DIPENDENTE.
PROPORZIONALITA’ DIRETTA
La più semplice relazione tra grandezze fisiche e’ la
relazione di PROPORZIONALITA’ DIRETTA.
Costruiamo una tabella per esprimere la relazione tra
due variabili x e y.
X
Y
0
0
1
4
2
8
3
12
4
16
5
20
Si può vedere che quando la variabile x raddoppia, anche la
variabile y raddoppia, quando x triplica, anche y triplica,
etc.
Quindi, se facciamo il rapporto y/x si può notare che
questo rapporto e’………………
costante
ed in questo caso vale 4.
y
k = ── = 4
x
Quando il rapporto tra due grandezze è costante si
dice che le due grandezze sono …………………….
DIRETTAMENTE PROPORZIONALI.
Due grandezze si dicono DIRETTAMENTE
PROPORZIONALI quando ………………
il loro RAPPORTO è COSTANTE.
y
── = k
x
Questa relazione si può esprimere anche come:
y=kx
N.B.: Rappresentando le due grandezze su di
un grafico cartesiano otteniamo una retta
passante per l’origine.
Viceversa, se su un grafico è rappresentata una
retta passante per l’origine, significa che le due
grandezze rappresentate sono
DIRETTAMENTE PROPORZIONALI.
y
0
x
L’inclinazione della retta rispetto all’asse X è detta
PENDENZA (possiamo approssimativamente indicarla
con l’angolo α) e dipende dal valore della costante k.
Più è grande il valore di k, maggiore è l’angolo che la
retta forma con l’asse X.
Se la pendenza è maggiore, significa che la grandezza rappresentata dalla variabile
dipendente (y) varia più rapidamente. Nella figura sottostante l’angolo β risulta > α,
per cui la retta rossa ha una pendenza maggiore della retta verde e quindi la
grandezza rappresentata dalla retta rossa varia più rapidamente dell’altra.
y
β
α
0
x
Altre relazioni matematiche
Se la retta NON passa per l’origine, la relazione tra le
due grandezze e’ detta ……………….
LINEARE.
dove a e b rappresentano dei valori costanti.
Costruiamo una tabella per esprimere la relazione tra
due variabili.
Prendiamo un recipiente già parzialmente pieno e
aggiungiamo acqua in modo costante. In questo caso la
quantità d’acqua V nel recipiente e il tempo t sono
grandezze correlate linearmente.
T (min)
V (litri)
0
3
1
5
2
7
3
9
4
11
In questo caso si vede che il rapporto tra y e x NON e’ costante;
la relazione tra x e y e’ espressa dalla formula:
y=k∙x+q
q praticamente rappresenta il punto in cui la retta attraversa
l’asse y (e per questo in matematica e’ detta …………………..
ORDINATA ALL’ORIGINE).
Nel nostro esempio si vede che y = 2x + 3 e quindi k = 2 e q = 3
(la nostra retta attraversa l’asse y nel punto di ordinata = 3).
PROPORZIONALITA’ INVERSA
Un’altra relazione tra due grandezze e’ la
PROPORZIONALITA’ INVERSA.
Costruiamo una tabella per esprimere la relazione tra
due variabili x e y
X
Y
10
600
20
500
30
400
40
300
50
200
60
100
Si può vedere che quando la variabile x raddoppia, la
variabile y dimezza, quando x triplica, y diventa 1/3, etc.
Quindi se facciamo il prodotto y ∙ x, si può notare che
questo prodotto e’ costante.
Nel nostro esempio il prodotto tra x e y e’ sempre = 6000.
y ∙ x = k = 6000
Quando il prodotto tra due grandezze e’ costante, si dice
che le due grandezze sono ……………….
INVERSAMENTE PROPORZIONALI.
Quindi due grandezze si dicono INVERSAMENTE
PROPORZIONALI quando ……………………
il loro PRODOTTO e’ COSTANTE.
y∙x=k
N.B.: Se rappresentiamo le due grandezze su di un grafico
cartesiano otteniamo un ………………….
ramo di iperbole.
Viceversa, se su un grafico e’ rappresentato un ramo di
iperbole, significa che le due grandezze rappresentate
sono……………..
INVERSAMENTE PROPORZIONALI.
PROPORZIONALITA’ QUADRATICA
L’ultima relazione che prendiamo in considerazione e’
la PROPORZIONALITA’ QUADRATICA.
Costruiamo una tabella per esprimere la relazione
tra due variabili x e y dove x e y rappresentano
rispettivamente il raggio e l’area di un cerchio.
L’area e il raggio di un cerchio sono legate da
proporzionalità quadratica. Al raddoppiare del
raggio l’area diventa 4 volte più grande, al triplicare
del raggio l’area diventa 9 volte più grande ….
dove a rappresenta una costante.
Quindi una grandezza y si dice che ha una proporzionalità
quadratica rispetto ad una grandezza x, quando, dividendo i
valori che assume la y per i corrispondenti valori di x al quadrato,
si ottiene sempre lo stesso valore k:
y
── = k
x2
oppure
y = k ∙ x2
Se rappresentiamo le due grandezze su di un
grafico cartesiano otteniamo una ………………
parabola.
Viceversa, se su un grafico e’ rappresentata
una parabola, significa che fra le due
grandezze rappresentate esiste una ………….
proporzionalità quadratica.
RIASSUMENDO
Due grandezze x e y sono direttamente
proporzionali quando………
il loro rapporto e’ costante;
la formula che esprime la relazione di proporzionalità
diretta è
y
── = k
x
Il grafico di y in funzione di x è……..
una retta passante per l’origine degli assi.
Due grandezze sono legate dalla relazione lineare
quando
y=k∙x+q
Il grafico di y in funzione di x e’ ……..
una retta NON passante dall’origine degli assi,
ma dal punto q (per questo q si chiama anche……..
ORDINATA ALL’ORIGINE).
Due grandezze x e y sono inversamente
proporzionali quando …………
il loro prodotto e’ costante;
la formula che esprime la relazione di
proporzionalità inversa e’
y∙x=k
Il grafico di y in funzione di x è………
un ramo di iperbole.
La proporzionalità quadratica e’ espressa
dalla relazione matematica
y
── = k
x2
Il grafico che esprime la relazione tra x e y e’
una …….
parabola.
THE END
1
Quando due grandezze sono direttamente
proporzionali?
A il loro prodotto è costante
B la loro somma è costante
C la loro differenza è costante
D il loro rapporto è costante
2
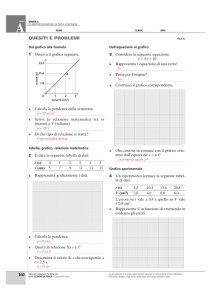
Nella figura sono rappresentate due grandezze x e
y correlate linearmente. Quale delle seguenti formule
descrive la relazione?
A y = 11 + 2x
B y = 2x
C y = 3x + 3
D y = 2x + 3
3
A
B
C
D
Quale relazione rappresenta la formula y = 3/x
proporzionalità diretta
proporzionalità inversa
proporzionalità quadratica
nessuna delle precedenti
4
Fra le seguenti grandezze solo due sono
direttamente proporzionali. Quali?
A il perimetro e il lato di un tavolo quadrato
B il raggio e l’area di un cerchio
C il volume di un cilindro e il raggio di base
D il numero degli studenti di una scuola e il numero
degli insegnanti
5
Se due grandezze sono inversamente
proporzionali, la loro rappresentazione grafica è:
A una semiretta non uscente dall’origine degli assi
B una semiretta uscente dall’origine degli assi
C una parabola
D un ramo di iperbole
6
Nella figura sono rappresentate due grandezze x e
y direttamente proporzionali. Quale delle seguenti
formule descrive la relazione?
A y = 4x
B y=x
C y = 2x
D y = 2x + 1
7
La grandezza y è funzione della grandezza x.
x
y
1
30
2
15
3
10
4
7,5
5
6
Quale delle seguenti affermazioni è corretta?
A y è direttamente proporzionale a x
B y è inversamente proporzionale a x
C y è proporzionale al quadrato di x
D y dipende linearmente da x