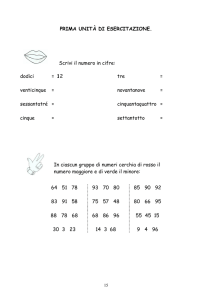
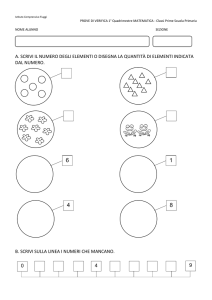
Ripetiamo…!
La divisibilità
Docente: Maura Roberta Orlando
Classe Seconda
ESERCIZI
Esercizio: Quali numeri sono multipli di 6?
12, 15, 6, 20, 26, 36, 45, 48, 63
Ricorda!!! Un multiplo di un numero naturale a è il prodotto di a per un qualunque
numero naturale.
Esercizio: Questi numeri sono tutti divisori di 36?
1, 2, 3, 4, 6, 9, 12, 18, 36
SI/NO perché: 36:1 =………. 36:2=……… 36:3=……. 36:4=……. 36:6=………. 36:9=……….
36:12=……. 36:18=......... 36:36=……….
Ricorda!!! Il numero naturale d è un divisore del numero naturale a, se a è un
multiplo di d (ovvero se i numeri dati dividono esattamente il numero 36)
Esercizio: Rispondi: quando un numero naturale è primo?..................... L’1 è un
numero primo? ………………….. Perché? ……………………………….
Risolvi i seguenti problemi
1. Costruisci in Excel una tabella con le misure di tutti i rettangoli che hanno area di
18 quadretti e i lati di misura INTERA. Quanti sono? Ora costruisci un diagramma
cartesiano ponendo x=base e y=altezza. Discuteremo in aula del risultato.
x (base)
y (altezza)
y
Ricordati di fissare
un’unità di misura
se lavori sul
quaderno!!!
0
x
2. Disegna sul quaderno una tabella con le misure di tutti i rettangoli che hanno
area di 36 quadretti e i lati di misura INTERA. Quanti sono? Ora costruisci un
diagramma cartesiano ponendo x=base e y=altezza. C’è qualcosa di uguale rispetto
all’esercizio precedente? C’è qualcosa di diverso?
ESERCIZI
Esercizio: Cerchia i numeri DIVISIBILI PER 2.
2, 13, 42, 1000, 45, 63, 33, 68, 74, 96, 3.
SCRIVI LA REGOLA:
Esercizio: Cerchia i numeri DIVISIBILI PER 3.
63, 23, 62, 99, 45, 36, 333, 44, 84, 56, 7.
SCRIVI LA REGOLA:
Esercizio: Cerchia i numeri DIVISIBILI PER 5.
5, 12, 15, 4560, 34, 23455, 111, 112, 115.
SCRIVI LA REGOLA:
Esercizio: Cerchia i numeri DIVISIBILI PER 10.
120, 3560, 78, 17770, 45, 305, 1005, 10006.
SCRIVI LA REGOLA:
Esercizio: Quando un numero è divisibile per 6? Quali regole che già conosci sono
utili? ………………………………………………………………………………………………………………………
Altre regole di divisibilità…
Un numero è divisibile per 4 quando le ULTIME 2 CIFRE A DESTRA formano un
numero divisibile per 4.
Esercizio. Evidenzia le ultime cifre a destra. Il numero è divisibile per 4? Verifica
effettuando la divisione.
Esempio. 312. 312. 12 è divisibile per 4. Infatti 312:4=78.
4540
1324
670 036
78 816
Un numero è divisibile per 11 quando la DIFFERENZA tra la SOMMA delle cifre di
POSTO dispari e quella di posto pari è 0 o un multiplo di 11.
Esempio. 165. (1+5)-6=6-6=0
Esempio. 92939. (9+9+9)-(2+3)=27-5=22
Esercizio. Prova con i seguenti numeri.
1397
209
Esercizio. Scrivi 5 numeri che siano divisibili per 11.
Completa la tabella
numeri
225
3000
176
99
385
550
726
1750
360
Sono divisibili per…
2
3
4
5
10
11
Tabella dei “primi” NUMERI PRIMI
Cercate di ricordare a memoria la prima riga e… stampate la
tabella!
Da tenere sempre nel quaderno.
Ricordiamo come si scompone un numero composto
1260
630
315
105
35
7
1
2
2
3
3
5
7
1260 = 2 x 2 x 3 x 3 x 7
1260 = 22 x 32 x 7
Esercizio. Esegui la scomposizione in fattori primi dei seguenti numeri:
42; 28; 56; 64; 81; 105; 121; 200; 240; 300; 528; 738; 990; 724; 1600
Esercizio. Risolvi il seguente problema. Andando in ufficio, ogni 15 giorni incontro
Andrea, ogni 7 giorni Anna e ogni 5 giorni Virginia. Oggi li ho incontrati tutti e tre.
Tra quanti giorni li incontrerò ancora tutti e tre nello stesso giorno?
Risposta: ……………………………………………… Perché? Cosa hai calcolato? ………………….
Scrivi la definizione di ciò che hai calcolato. ……………………………………………...............
……………………………………………………………………………………………………………………………….
ESERCIZI
Esercizio: Indica quali delle seguenti coppie è costituta da numeri che NON sono
primi, ma sono PRIMI FRA LORO:
a) 7; 9
b) 41; 53
c) 15; 14
Esercizio: Indica quale tra i seguenti procedimenti è corretto per trasformare il
prodotto 45 x 48 in un prodotto di fattori primi:
a) 5x9 x12x4 = 5x3x3x6x2x4 = 5x3x3x6x2x2x2
b) 15x3x16x3 = 5x3x3x8x2x3 = 5x3x3x2x2x2x2x3
c) 9x5x6x8 = 3x3x5x6x4x2 = 3x3x5x2x3x4x2
Esercizio: Calcola il m.c.m. dei seguenti numeri:
a) 25-30; 84-21; 15-8; 33-22
b) 10-20-30; 5-6-7; 8-16-3; 50-100-25; 63-7-21; 81-4-9.
Alcune terne sono casi particolari. In quale caso moltiplichi tra di loro tutti i
numeri senza scomporli? E in quale caso il m.c.m. corrisponde al numero più
grande della terna?
Ex 1. Write the factors for each of these numbers:
16 ………………
18 ……………..
20 ……………..
24 ……………..
Ex 2. Then write the common factors for each pair of numbers:
a) 16; 18 ……………………
b) 20; 24 ……………………
Ex 3. Finally write the least common multiple (l.c.m.) for each pair:
a) 16; 18 ……………………
b) 20; 24 ……………………
Good job!