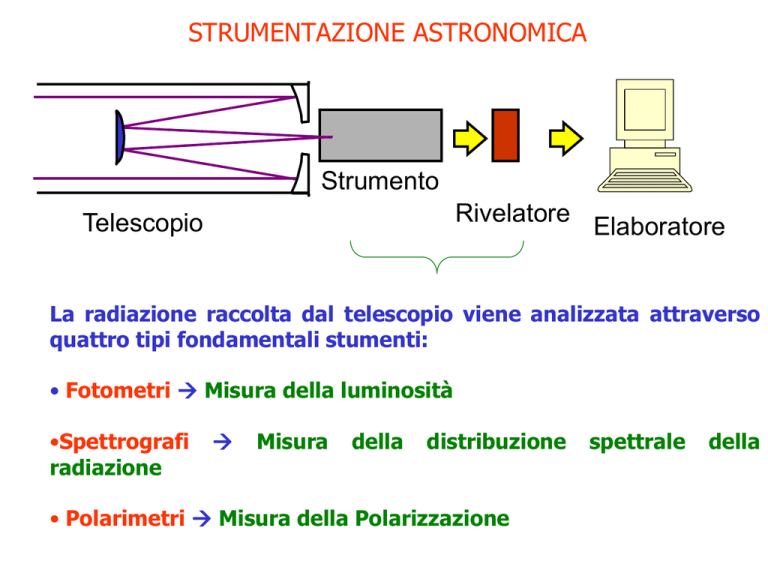
STRUMENTAZIONE ASTRONOMICA
Strumento
Rivelatore
Telescopio
Elaboratore
La radiazione raccolta dal telescopio viene analizzata attraverso
quattro tipi fondamentali stumenti:
• Fotometri Misura della luminosità
•Spettrografi
radiazione
Misura
della
distribuzione
• Polarimetri Misura della Polarizzazione
spettrale
della
STRUMENTAZIONE PER FOTOMETRIA
I principali strumenti per fotometria sono:
• Camera Fotografica Largamente usata fino agli anni 1990
•Rivelatore: Emulsione fotografica
• Fotometro Fotoelettrico Rivelatore: Fotomoltiplicatore
• Camera CCD Rivelatore: Charge Coupled Device (CCD)
Rivelatore: Dispositivo in grado di convertire i fotoni in un segnale
misurabile (tensione, corrrente, ecc.)
STRUMENTAZIONE PER FOTOMETRIA
I parametri che caratterizzano un rivelatore sono:
•Efficienza Quantica
•Linearità della risposta
•Banda Passante
•Intervallo Dinamico
•Rumore
N out ( )
q ( )
N in ( )
STRUMENTAZIONE PER FOTOMETRIA
Emulsione
Fi
(gelatina + AgBr)
ca. 100 mm
vetro
Ft
LASTRA FOTOGRAFICA
•Dispositivo non lineare
•Grandezza misurata: Densità
•Efficienza quantica: ca. 1-10%
Fi
D log( )
Ft
•Errore fotometrico: ca. 5%
•Dispositivo panoramico sky survey
STRUMENTAZIONE PER FOTOMETRIA
FOTOMOLTIPLICATORE
Principio di funzionamento: Effetto Fotoelettrico
STRUMENTAZIONE PER FOTOMETRIA
FOTOMOLTIPLICATORE
•Dispositivo lineare
•Grandezza misurata: corrente elettrica
•Efficienza quantica: >20%
•Errore fotometrico: ca. 1%
•Dispositivo a canale singolo un oggetto alla volta
•Alta risoluzione temporale
STRUMENTAZIONE PER FOTOMETRIA
IL CCD
I Charge Coupled Devices (CCDs)
furono inventati negli anni 1970
come dispositivi di memoria. Ma
data la loro sensibilità alla luce
furono subito usati in campo
astronnomico come rivelatori di
radiazione. Il CCD converte la
radiazione incidente in pacchetti di
elettroni che poi vencono convertiti
in un segnale video che viene
digitalizzato e immagazzinato in
un file immagine in un PC.
Opportuni programmi di analisi
immagini
permettono
di
effetturare misure quantitative.
STRUMENTAZIONE ASTRONOMICA
CCD
•Dispositivo lineare
•Grandezza misurata: tensione
•Efficienza quantica: >90%
•Errore fotometrico: ca. 1%
•Dispositivo panoramico
•bassa risoluzione temporale ma L3CCD
STRUMENTAZIONE ASTRONOMICA
I Rumori del CCD
•Rumore di lettura (readout-noise)
•Rumore termico (dark noise)
Riduzione dei dati;
I (i, j ) raw Bias (i, j ) Dark (i, j )
I (i, j )
F
Flat (i, j )
Profilo Stellare
L’inquinamento Luminoso
L’inquinamento Luminoso
L’inquinamento Luminoso
Crescita della luminanza
artificiale del cielo nella
pianura veneta in unità
relative determinata in base
alle misure di archivio di
brillanza del cielo presso
l'Osservatorio Astrofisico di
Asiago e lOsservatorio
Astronomico dell'Ekar
(Cinzano 1998)
Effetti dell’Atmosfera
Effetti dell’Atmosfera
L’atmosfera terrestre influenza l’osservazione astronomica attraverso effetti di:
•OPACITA’
assorbimento
•DIFFUSIONE
chiarore diurno, inquinamento luminoso
•EMISSIONE TERMICA
oss. mm e IR
•TURBOLENZA
scintillazione, seeing
•IONIZZAZIONE oss. radio
L’opacità e la turbolenza influenzano l’intensità e la direzione della radiazione e il
loro effetto dipende dal tempo e dalla posizione dell’osservatore.
Su scale temporali molto brevi (<0.1 sec), gli effetti di opacità e turbolenza
possono essere considerati come la composizione di due effetti, uno costante e
uno variabile
•OPACITA’
•TURBOLENZA
: Estinzione (cost) +Scintillazione (var) Instensità
: Rifrazione (cost) +Seeing (var)
Direzione
Effetti dell’Atmosfera
Lo strato di atmosferico che influenza le osservazioni astronomiche nella banda
del visibile, è la TROPOSFERA, cioè i primi 15 km (sebbene l’altezza della
tropopausa varia tra 8 km alle alte latitudini ai 18 km all'equatore), dove c'è
circa il 90% della massa atmosferica.
RIFRAZIONE
Nell’approssimazione di atmosfera a
strati piani e paralleli, ognuno dei
quali caratterizzato da un indice di
rifrazione ni, si può dimostrare che la
deviazione angolare totale subito da
un raggio hdipende solo dall'indice di
rifrazione vicino al suolo
z - z’ = R
con:
R = (nf -1)tan z’
nf ~ 1.00029
Il Seeing
La presenza di turbolenza nell’atmosfera determina lo
“scinltillio” delle stelle e il “seeing”.
Il “seeing” determina la dimensione del più piccolo dettaglio
visibile in un’immagine.
Il Seeing
La misura del seeing:
DIMM
Il Seeing
Fronte d’onda incidente
La tubolenza può essere descritta attraverso
il parametro di Fried r0 definito come la distanza
entro la quale la distrorsione del fronte d’onda
(in fase) ha un valore quadratico Medio di 1 rad2.
Strato turbolento
r0
Fronte d’onda deformato
Fase F
PSF telescopio+atmosfera
r0 5 cm seeing cattivo
Specchio telescopio: D
D >> r0
r0 20 cm seeing buono
Ottica Adattiva
La possibilità di correggere il seeing
indagata già nel 1953, ma l’applicazione
pratica si è avuta solo negli ultimi 10
Anni.
Telescopio Spaziale
sedna
TELESCOPI – Interferometri
Aumento della risoluzione
Nel tempo
Calcolo dell’Altezza e Azimut di una stella
a = Ascensione retta di un’oggetto
d = Declinazione di un’oggetto
f = Latitudine dell’osservatore
L = Longitudine dell’osservatore (+ Est, - Ovest)
Data: Y = anno, M = mese, D = giorno
Tempo: UT = Tempo universale
UT = Tempo Locale – FusoOrario
(FusoOrario: - Ovest, + Est di Greenwich)
JD = Giorno Giuliano
A = int(Y/100)
B = 2 - A + int(A/4)
JD = int(365.25 (Y + 4716)) + int(30.6001 (M + 1) + D + B - 1524.5
qo = Tempo Siderale di Greenwich
T = (JD + UT/24 - 2,451,545.0)/36525 (secolo giuliano)
qo = 280.46061837 + 360.985647366 29 ( JD -2,451,545.0) + 0.000387933 T2 - T3/38,710,000
q= Tempo siderale locale
q = qo + L
H = Angolo Orario
H=q-a
•A = Azimut dell’Oggeto
•a = Altezza dell’Oggetto
tan A = sin H / (sin H sin f - tan d cos f )
sin a = sin f sin d + cos f cos d cos H
Sensibilità della strumentazione
Rapporto Segnale/Rumore e sensibilità
Si ricorda che indipendentemente dalla costanza o meno di una sorgente luminosa, i fotoni
arrivano su di un rivelatore in modo random. Cioè non è possibbile determinare con esattezza
nè il numero di fotoni che arriveranno sul rivelatore nell’unità di tempo (rumore temporale)
nè la loro posizione di arrivo (rumore spaziale).
La probababilità che in un intervallo di tempo Dt arrivino sul rivelatore n0 fotoni è data dalla
distribuzione di Poisson:
e N N n0
P ( n0 )
n0 !
N (Rumore)
Dove N è il numero medio di fotoni arrivati nel tempo Dt. La presenza ineliminabile del rumore
fotonico introduce un’incertezza in ogni misura della radiazione proveniente da un astro.
Sensibilità della strumentazione
Calcolo del rapporto segnale rumore:
dove:
(Adattato dal sito dell’ESO Exposure Calculator)
Sensibilità della strumentazione
Il numero di conteggi attesi da una sorgente e dal cielo può essere stimato attarverso le
seguenti relazioni
Dove (caso imaging):
N è il numero di fotoni per pixel,
F è il flusso incidente [W/m2/mm];
Di = larghezza di banda del filtro [mm];
T = tempo di esposizione [s];
E = efficienza,
S = area del telescopio [m2],
Wi angolo solido sotteso da ogni pixel;
P = energia di ogni fotone.
N è dato in in [e-/pixel].
(Adattato dal sito dell’ESO Exposure Calculator)
Sensibilità della strumentazione