Raggi cosmici
La terra viene investita da un flusso di particelle
cariche e neutre di alta energia di origine extraterrestre
Il flusso di tali particelle è pari a circa 1000 per metro
quadro per secondo (90% protoni, 9% elio ed il resto
nuclei pesanti.
I raggi cosmici hanno avuto un ruolo storico nello sviluppo della
fisica subnucleare, ma le domande fondamentali :
•
da dove provengono ?
•
quali sono i meccanismi di accelerazione?
aspettano ancora risposte completamente esaurienti
Spettro d’energia
GeV
TeV
PeV
EeV
Discontinuita’ nello spettro
ginocchio
caviglia
Spesso riportato spettro
moltiplicato per E2 o E2.5 .
Alquanto rischioso,
poiche’ fortemente
influenzato da errori
sistematici in energia
misurata in esperimenti
diversi.
Composizione elementare
Composizione elementare
dei raggi cosmici
Curva continua: distribuzione corretta
tenendo conto del taglio a basse energie
introdotto dal campo magnetico
Problemi aperti
Domande fondamentali:
1) Da dove vengono?
2) Quali sono i meccanismi di accelerazione?
Risposte di prima approssimazione :
1) Essenzialmente di provenienza galattica- (giroraggio)
2) Meccanismo di Fermi
Confinamento dei RC nella Galassia
Il campo magnetico galattico è circa
3mG ed e’ mediamente parallelo al
braccio della spirale della galassia,
con grandi fluttuazioni
1pc=3.1 x 1013 km
1anno-luce=9.5 1012 km
Confinamento dei RC nella Galassia
Campo magnetico galattico uguale a circa 3mG
Raggio dell' orbita :
γmv 2
ZevB con v c
r
mc
E
pc 1
r
ZeB ZeBc Ze Bc
E GeV
0.3 BT Z
R Rigidita'
Per una particella di 100 GeV e B 3mG 3 10-10 T :
Se protone
R 100 GV ; r 3.2 10 5 pars. ( pc)
Se nucleo di Fe
R
4 GV ; r 1.2 10 6 pc
Se energia 100 TeV rP 0.03 pc spessore del disco Galattico (300 pc)
Confinamento dei RC nella Galassia
Protone da 5.1019 eV (50 PeV) in un campo di 3mG
300 pc
30 kpc
Confinamento dei RC nella Galassia
Protone da 5.1019 eV (50 PeV) in un campo di 3mG
r=18 kpc: confrontabile con le dimensioni della
Galassia
Per energie elevate ci aspettiamo una qualche anisotropia
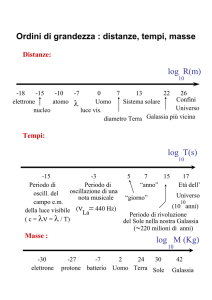
Sistemi di coordinate[1]
Coordinate equatoriali:
ascensione retta e
declinazione
Ascensione retta R.A. (a)
declinazione d
Tempo siderale diverso
dal tempo solare
Sistemi di coordinate[2]
Coordinate equatoriali:
ascensione retta e declinazione
Ascensione retta R.A. (a)
declinazione d
Relazione tra
[ascensione retta – declinazione]
e [zenith (q) - azimuth(f)]
dL e’ la latitudine locale
tS e’ il tempo siderale locale
Sistemi di coordinate[3]
Coordinate Galattiche:
ascensione retta e declinazione
latitudine galattica b
longitudine galattica l
Sistemi di coordinate[4]
Relazione tra
[ascensione retta-declinazione]
e [latitudine-longitudine galattica]
Definizioni dell’anisotropia
Rivelatore che opera in modo uniforme rispetto al tempo siderale
efficienza dipende fortemente dalla declinazione d, ma non dalla R.A.
Si cerca allora eventuali asimmetrie in quest’ultima (chiamiamola q)
Analisi armonica N eventi ad angoli qi
Ampiezza della prima armonica :
r a 2 b2
12
; dove :
N
N
i 1
i 1
a 2 N cos i ; b 2 N sin i
Fase :
b
a
Si usa determinar e prima e seconda armonica in funzione dell' energia,
attraverso conteggio del rate in funzione del tempo siderale e fit :
f tan -1
2 t
2 t
R(t ) A B sin
f1 C sin
f2
24
12
B, f1 ampiezza e fase della prima armonica
C,f2 ampiezza e fase della seconda armonica
Normalment e si riporta B/A in funzione dell' energia, in coordinate galattiche .
Anisotropia
Log E (eV)
12
14
16
18
19-20
d(%)
~0.05
~0.1
~0.6
~2
~20
Anisotropia dei raggi cosmici
Le asimmetrie misurate ad oggi sono molto piccole e crescono
all’aumentare dell’energia.
Al di sotto di circa 10 GeV gli effetti del campo magnetico
solare mascherano la direzione di provenienza.
Per energie elevate, il massimo dell’asimmetria sembra puntare
nella direzione del supercluster locale di galassie.
Anisotropia ad alte energie [Agasa+..]
Asimmetria ad alte energie
(E>4x1019 eV)
Dati di AGASA (47) + Haverah Park (27)+ Yakutsk (12)+ Volcano Ranch (6)
A sinistra: curva continua
distribuzione in latitudine
supergalattica degli eventi
attesi dai vari esperimenti
in assenza di anisotropie.
A destra: distribuzione in
latitudine supergalattica
delle Galassie entro
80 Mpc.
Distribuzione di materia
concentrazione di galassie
entro 20o dal piano
supergalattico.
Distribuzione dei raggi c.
nessun eccesso
Anisotropia ad alte energie [Agasa+..]
Distribuzione in bins angolari di 1o
Ora le Galassie “vicine”
non mostrano alcuna
particolare concentrazione,
mentre i raggi cosmici hanno
un picco entro 10 dal piano
supergalattico
Large-scale isotropy
Small-scale clustering
Anisotropia ad alte energie{Agasa+...]
Direzioni d’arrivo di 114 eventi con E>4x1019 eV
Eventi indicati con cerchietti
grandi E>1020 eV
Arrival Directions of Cosmic Rays above 4x1019 eV
galactic plane
supergalactic plane
Akeno 20 km2, 17/02/1990 – 31/07/2001, zenith angle < 45o
Red squares : events above 1020 eV, green circles : events of (4 – 10)x1019 eV
Shaded circles = clustering within 2.5o.
Chance probability of clustering from isotropic distribution is < 1%.
Anisotropia [Agasa]
Correlazioni angolari tra sorgenti diverse
Small-scale clustering
Radio-Loud Galaxies
Angular correlation of ultra-high energy cosmic rays with
compact radio-loud quasars
Amitabh Virmani,
Astropart. Phys.17,
489, 2002
Composizione e tempo di “residenza” dei RC nella
Galassia
Nuclei primari carbone ossigeno ferro (prodotti dalla nucleosintesi
stellare).
Nella radiazione cosmica si trovano Litio, Berillio e Boro facilmente
prodotti da reazioni di spallazione.
Il rapporto primari a secondari porta alle seguenti conclusioni:
• I raggi cosmici nella loro vita attraversano circa 5-10 g/cm2
• Lo spessore attraversato diminuisce al crescere dell’energia
Lo spessore trasversale della galassia è circa 10-3 g/cm2
• RC. attraversano migliaia di volte la galassia
• RC alta energia passano minor tempo nella galassia
Tempo di residenza dei RC
La misura del rapporto degli isotopi instabili con quelli
stabili di nuclei “secondari” permette di valutare il
tempo di residenza tconf. dei R.C: nella galassia.
In particolare l’isotopo più usato come orologio
cosmico è il 10Be che ha una vita media di 3.9x106 anni
Calcolo della densita’ d’energia
Spettro dei protoni, corretto per il taglio magnetico
E
1.8
dE
GeV
dFp
2.7 0.05
Densita' d' energia : CR
1.28 10 12 erg / cm 3
cm 2 s 1sr 1GeV 1
4
c
4
E
dE
1 dE
c
dFp
2.7
10
3
E
1
.
8
E
dE
8
10
GeV
cm
1
Energetica dei Raggi Cosmici
Densità di energia locale dei raggi cosmici:
E=0.8 eV/cm3
Densita’ di energia magnetica:
B=0.2 eV/cm3
Densita’ di energia cinetica del gas interstellare:
gas=1.0 eV/cm3
Densita’ d’energia luminosa:
L=0.3 eV/cm3
Densita’ d’energia della radiazione cosmica di fondo:
CMB=0.3 eV/cm3
Coincidenze casuali ?
Parametrizzazione dello spettro energetico
Spettro dei protoni, corretto per il taglio magnetico
2.7 0.05
E
1.8
cm 2 s 1sr 1GeV 1
dE
GeV
da cui si ottiene una luminosita ':
dFp
Lcr 1.5 10 41 erg s 1
Compatibile con l’energia liberata nelle esplosioni di SN nella
Galassia:
1 SN ogni 50 anni (1.58x109 s)
Energia/SN=1051 erg
Energia media liberata/s=1051/1.58x109=6x1041 erg/s
Ammettendo un’efficienza media di conversione del 25%
LSN=1.5x1041 erg s-1
(Ginzburg e Syrovatskii -1964)
Calcolo della luminosita’
Spettro dei protoni, corretto per il taglio magnetico
E
1.8
dE
GeV
dFp
Luminosita ': LCR
2.7 0.05
cm 2 s 1sr 1GeV 1
1
t conf .
RC dV
dFp
4
1
E
dE dV
c t conf . dE
Densita' colonnare vista da raggi cosmici di energia E : X ( E ) 6.9 E 0.5 g cm 2
X (E)
dove : X ( E ) dx c t conf . t conf .
; ne segue :
LCR
dFp
1
4 dV
E
dE
X E dE
9
dV
massa
totale
del
gas
nella
Galassia
:
M
4
.
8
10
MS
gas
LCR 1.5 10 41 erg s 1
Accelerazione dei Raggi Cosmici
Accelerazione negli shock di SN ?
Possibile solo fino a circa 1015 eV
Energie piu’ elevate ?
Interazione con piu’ SNR’ fino a 1018 eV
Alle energie piu’ elevate: prevalentemente nuclei
Vincoli sulle possibili sorgenti:
Campo magnetico B nella zona dello shock; dimensione R
della zona di accelerazione
E=0.9 ZBR bc
(E in EeV, B in mG ed R in kpc. b = velocita’ dello
shock) . Per b fissato
logB~logE-logR (Hillas plot)
In un grafico di logB vs logR rette parallele, aventi intercetta
data da logE.
Hillas plot