S - Emilio Tomasini

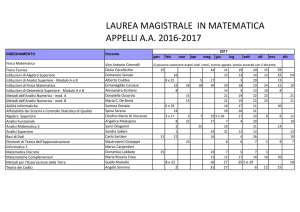
Finanza Aziendale – Bologna – Informatica per il management
PARTE PRIMA
INTRODUZIONE AL RISCHIO E AL RENDIMENTO
COSTRUZIONE DI PORTAFOGLI DI INVESTIMENTO IN
BASE A MODELLI DI DIVERSIFICAZIONE
Dott. Domenico Dall’Olio
[email protected]
1
Il pilastro fondamentale degli investimenti
Finanza Aziendale – Bologna – Informatica per il management
E’ tutta una questione di rischio e di rendimento
Nell’effettuare un investimento solitamente l’investitore si chiede quanto potrà
ricavarne; difficilmente l’aspettativa di profitto si basa su criteri scientifici: più
spesso è il riflesso di una speranza, motivata probabilmente dal desiderio di
soddisfare un bisogno di qualche genere.
Pochi investitori fanno considerazioni più ragionate e si pongono la domanda
più giusta: quanto posso sperare di guadagnare in relazione al rischio che sto
sopportando?
La regola fondamentale dei mercati finanziari è che dove c’è un rendimento c’è
un rischio; ribaltando il discorso, se non c’è rischio, non c’è rendimento.
Dott. Domenico Dall’Olio
[email protected]
2
Il pilastro fondamentale degli investimenti
Finanza Aziendale – Bologna – Informatica per il management
In condizioni di mercato “normale” rischio e rendimento sono sostanzialmente
proporzionali: al crescere della richiesta di profitto deve crescere in proporzione
il rischio da tollerarsi; allo stesso modo, se il rischio aumenta, l’aspettativa
reddituale aumenta in proporzione.
Qui però si innesta un problema concettuale molto forte: rischio e rendimento
reali non sono perfettamente prevedibili nel momento in cui si effettua un
investimento; in effetti si possono soltanto fare congetture.
La realtà dei fatti sarà nota soltanto dopo che si sarà palesata.
Dott. Domenico Dall’Olio
[email protected]
3
Pubblicità… ingannevole
Finanza Aziendale – Bologna – Informatica per il management
Oggi su molti siti internet si è tempestati di banner e riquadri pubblicitari che
inneggiano al profitto facile in borsa: si vede spesso l’immagine del
professionista di turno che nella pausa pranzo ha realizzato un profitto di 2000
euro sul mercato delle valute, investendo soltanto 200 euro, un decimo.
E’ pubblicità ingannevole sotto diversi punti di vista:
• non parla del rischio sopportato per ottenere quel rendimento (ammesso e non
concesso che sia reale): non spiega infatti che simili operazioni si possono fare
soltanto su conti a leva finanziaria, che moltiplicano per diverse volte i profitti
potenziali, ma anche i rischi potenziali;
• non spiega che purtroppo non bastano 200 euro per fare operazioni di quel
genere, perché la leva finanziaria non è un regalo, e non è per tutti;
• non dice come è andata il giorno dopo…
Dott. Domenico Dall’Olio
[email protected]
4
Un piccolo passo avanti
Finanza Aziendale – Bologna – Informatica per il management
Un rendimento del 15-20% annuo è già un ottimo risultato, se ottenuto con
costanza, ma a due condizioni:
1. che il rischio potenziale sia proporzionato a tale ritorno atteso
2. che il risultato effettivo non sia troppo diverso da quello atteso
In merito alla seconda condizione, un esempio servirà a chiarire il concetto. Si
considerino due investimenti alternativi, uno che rende il 20% l’anno per due
anni consecutivi – per un totale del 40% (non consideriamo la capitalizzazione
dei profitti) – e uno che rende il 50% il primo anno e perde il 10% il secondo
anno. Il risultato finale è lo stesso, ma non sono affatto equivalenti!
Con il primo si hanno infatti utili stabili, con il secondo redditi imprevedibili. Non
conta solo dove si arriva, ma anche come ci si arriva!
Dott. Domenico Dall’Olio
[email protected]
5
Un piccolo passo avanti
Finanza Aziendale – Bologna – Informatica per il management
In merito alla prima sono necessarie alcune precisazioni fondamentali: il rischio
sopportabile a fronte di un rendimento atteso può non essere lo stesso per tutti
gli investitori (di solito in effetti non lo è). In altri termini, ci sono investitori che
hanno diversi gradi di tolleranza al rischio, quindi non hanno pari aspettative
reddituali a parità di rischio.
Ma d’altro canto la percezione del rischio è spesso soggettiva, quanto a dire che
a fronte di uno stesso investimento due diversi investitori potrebbero percepire
rischi diversi.
I principali modelli di comportamento di mercato suggeriscono che due
investimenti dotati dello stesso livello di rischio debbano offrire lo stesso livello
di rendimento.
Dott. Domenico Dall’Olio
[email protected]
6
Un piccolo passo avanti
Finanza Aziendale – Bologna – Informatica per il management
E viceversa, due investimenti che offrono lo stesso livello di rendimento devono
avere lo stesso rischio.
Nel mondo reale ciò non sempre si verifica, dato che le asimmetrie informative
rendono difficile per gli investitori comparare in piena consapevolezza tutti gli
investimenti alternativi possibili.
Quindi rimangono alcune questioni aperte:
1. come si definisce il rischio?
2. come si possono formulare aspettative di rendimento?
3. è possibile modellizzare questi concetti?
4. i modelli funzionano?
Dott. Domenico Dall’Olio
[email protected]
7
Un passo indietro: concetti statistici di base
Finanza Aziendale – Bologna – Informatica per il management
La finanza rappresenta uno dei tanti campi in cui gli eventi possibili sono dotati
di un’ampio margine di incertezza, dunque si presta all’uso della statistica.
L’incertezza degli eventi implica che essi non sono sempre prevedibili. Va detto
però che “imprevedibilità” non è sinonimo di “impossibilità di previsione”: si
consideri ad esempio il lancio di una moneta; non si può essere certi del
risultato, ma si possono fare ipotesi su di esso.
Queste assunzioni sono basate su criteri probabilistici, grazie ai quali si può
calcolare una qualche misura di confidenza per un risultato specifico.
Supponiamo di lanciare un dado: nessuno può prevedere il numero che uscirà,
ma si può calcolare la probabilità di ottenere un 3 (probabilità di un evento
singolo), o che il risultato sia compreso tra 2 e 5 (probabilità di un intervallo).
Dott. Domenico Dall’Olio
[email protected]
8
Le due facce della statistica
Finanza Aziendale – Bologna – Informatica per il management
La statistica può essere divisa in due branche: inferenziale e descrittiva
La statistica inferenziale permette di formulare ipotesi su una popolazione (di
persone o di qualsiasi altra famiglia di elementi) basate sullo studio di un
campione. Le conclusioni non sono certezze, bensì affermazioni effettuate in
base a misure probabilistiche. Due problemi chiave di questo approccio sono la
scelta di un campione rappresentativo, e l’assunzione di ipotesi in merito alla
distribuzione di probabilità dei dati della popolazione.
La statistica descrittiva viene utilizzata per analizzare dati a prescindere dal
modello probabilistico sottostante ad essi e dal fatto che i dati provengano da un
campione o dalla popolazione. L’obiettivo è ridurre i dati ad alcuni parametri e
grafici di sintesi. Questa è la statistica che ci interessa oggi.
Dott. Domenico Dall’Olio
[email protected]
9
La definizione classica di probabilità
Supponiamo di lanciare un dado; vi sono sei risultati possibili, ciascuno dei quali dotato
Finanza Aziendale – Bologna – Informatica per il management
della stessa probabilità (se il dado non è truccato ovviamente): 1/6.
Questa affermazione si basa sulla cosiddetta definizione classica di probabilità: la
probabilità di un evento è data dal numero di casi favorevoli diviso per il numero di casi
possibili.
Andando a fondo nella questione, ciò che in effetti ci si può attendere è che la misura
classica della probabilità divenga sempre più accurata al cescere del numero di
osservazioni: supponete di lanciare un dado 100 volte e che escano cinque volte ciascuno
i numeri da 1 a 5 e 75 volte il numero 6. Potreste dire che il dado è truccato?
Ovviamente no, perché la definizione classica di probabilità riflette un comportamento
asintotico: la probabilità di un evento è si il numero di casi favorevoli diviso per il numero
di casi possibili, ma dopo un elevato numero di osservazioni. Maggiore quel numero, più
elevata l’affidabilità del calcolo probabilistico.
Dott. Domenico Dall’Olio
[email protected]
10
Grafici di frequenza
Finanza Aziendale – Bologna – Informatica per il management
Le probabilità dei singoli eventi relativi al lancio di un dado possono essere
poste su un grafico che riporti gli eventi sull’asse orizzontale e le rispettive
probabilità su quello verticale:
20.00%
15.00%
10.00%
5.00%
0.00%
1
Dott. Domenico Dall’Olio
[email protected]
2
3
4
5
6
11
Un passo avanti
Finanza Aziendale – Bologna – Informatica per il management
Ora supponiamo di lanciare due dadi. Questa volta ogni singolo evento può
manifestarsi in modi diversi, considerando la posizione specifica di ciascun
dado.
Tutti i risultati possibili possono essere rappresentati come segue:
esito
f
P
2
1
2.78%
3
2
5.56%
4
3
8.33%
5
4
11.11%
6
5
13.89%
7
6
16.67%
8
5
13.89%
9
4
11.11%
10
3
8.33%
11
2
5.56%
12
1
2.78%
Dott. Domenico Dall’Olio
[email protected]
20.00%
15.00%
10.00%
5.00%
0.00%
2
3
4
5
6
7
8
9
10
11
12
12
Ancora un passo avanti
Finanza Aziendale – Bologna – Informatica per il management
Supponiamo ora di lanciare tre dadi. Vediamo i dati e il grafico:
esito
f
P
3
1
0.46%
4
3
1.39%
5
6
2.78%
6
10
4.63%
7
15
6.94%
8
21
9.72%
9
25
11.57%
10
27
12.50%
11
27
12.50%
12
25
11.57%
13
21
9.72%
14
15
6.94%
15
10
4.63%
16
6
2.78%
17
3
1.39%
18
1
0.46%
Dott. Domenico Dall’Olio
[email protected]
14.00%
12.00%
10.00%
8.00%
6.00%
4.00%
2.00%
0.00%
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18
13
Misure di posizione e dispersione
Finanza Aziendale – Bologna – Informatica per il management
Una distribuzione di valori può essere sintetizzata utilizzando parametri noti
come misure di posizione e di dispersione; detti anche statistiche, essi sono la
media, la mediana, la moda, la varianza e la deviazione standard.
I primi tre possono essere visti come centri di gravità della distribuzione, gli altri
come gradi di dispersione dei dati intorno a quei centri di gravità.
La media viene anche detta valore atteso: si tratta del valore che più ci si
aspetta di osservare nel caso di una nuova osservazione.
La dispersione indica il grado di affidabilità della media: minore la dispersione,
maggiore la probabilità di osservare nuovi valori pari o molto prossimi alla
media; viceversa, maggiore la dispersione, maggiore la probabilità di osservare
nuovi valori anche molto distanti dal valore atteso.
Dott. Domenico Dall’Olio
[email protected]
14
Cosa c’entra tutto ciò con la finanza?
Finanza Aziendale – Bologna – Informatica per il management
Tutti i concetti precedentemente espressi si applicano anche alla finanza.
Se infatti la distribuzione dei valori è la distribuzione dei rendimenti giornalieri di
una serie finanziaria, allora il valore atteso è il rendimento atteso da un giorno
all’altro e la dispersione, detta volatilità, è una misura del grado di affidabilità di
quella aspettativa.
La statistica applicata alle serie finanziarie può quindi dirci quale rendimento
attenderci da un investimento, e con quale probabilità.
Questa probabilità può essere determinata sulla base di un modello (ed è ciò
che fa la moderna ingegneria finanziaria), oppure sulla base delle osservazioni
storiche.
Dott. Domenico Dall’Olio
[email protected]
15
Media, mediana e moda
Finanza Aziendale – Bologna – Informatica per il management
Si definisce media aritmetica di una distribuzione di n valori la quantità:
1 n
x   xi
n i 1
Il valore mediano di una serie di n termini ordinati in senso crescente è il valore
centrale della serie (se n è dispari), o la media dei due centrali (se n è pari). La
mediana è il valore che divide in due la distribuzione.
La moda è il valore che appare con la maggior frequenza. Una distribuzione può
essere a-modale (lancio di un dado), oppure avere una (due dadi) o più mode
(tre dadi).
Dott. Domenico Dall’Olio
[email protected]
16
Varianza e deviazione standard
Finanza Aziendale – Bologna – Informatica per il management
La varianza di una distribuzione di valori è una misura di dispersione attorno al
valor medio; la varianza si calcola come distanza quadratica media dalla media:
n
1
2
2
VAR( X )   x   xi  x 
n i 1
Trattandosi di una misura quadratica la varianza non può essere confrontata
con i valori della distribuzione. Quindi in molti casi è consigliabile calcolare la
deviazione standard, data dalla radice quadrata della varianza:
1 n
2
xi  x 
x 

n i 1
Dott. Domenico Dall’Olio
[email protected]
17
Dipendenza e indipendenza
Finanza Aziendale – Bologna – Informatica per il management
Spesso capita che su uno stesso gruppo di elementi vengano osservate più
variabili.
Una curiosità che può sorgere in simili situazioni è se esista o meno un certo
grado di correlazione tra quelle variabili. In altre parole è interessante chiedersi
se quelle due variabili siano in qualche modo dipendenti l’una dall’altra, o no.
Il grado di correlazione, o di dipendenza, può essere in prima istanza giudicato
in termini qualitativi, semplicemente mettendo su un grafico le due variabili, una
per ciascun asse, e disegnando un punto sul grafico per ogni osservazione. Se
a prima vista è possibile stabilire che le due variabili seguono le stesse regole,
allora si può assumere l’esistenza di un qualche tipo di correlazione tra esse.
Dott. Domenico Dall’Olio
[email protected]
18
Covarianza e correlazione
Finanza Aziendale – Bologna – Informatica per il management
La correlazione in finanza è un fenomeno molto diffuso, dato che, come
vedremo, gli andamenti dei singoli titoli quotati in una borsa tendono a muoversi
in modo per così dire simbiotico la maggior parte delle volte.
La covarianza e la correlazione sono due varianti della stessa misura: quanto, in
media, le due variabili dipendano l’una dall’altra.
In altri termini esse misurano quanto la variabilità di una delle due variabili è
originata dalla variabilità dell’altra.
Ancora, quanto il variare dell’una possa essere spiegato come conseguenza del
variare dell’altra.
Dott. Domenico Dall’Olio
[email protected]
19
Covarianza e correlazione
Finanza Aziendale – Bologna – Informatica per il management
Come per varianza e deviazione standard, così per covarianza e correlazione la
scelta dipende dall’unità di misura: la covarianza è una misura quadratica, e in
quanto tale non è spesso confrontabile con i dati di origine; la correlazione è
invece un numero puro, quindi un indice confrontabile con i dati.
COVAR( X , Y )   xy
1 n
   xi  x  yi  y 
n i 1
 xy
CORR ( X , Y )   xy 
 x y
Dott. Domenico Dall’Olio
[email protected]
20
Correlazione
Finanza Aziendale – Bologna – Informatica per il management
La correlazione oscilla tra -1 e 1 (o tra -100% e +100%).
Una correlazione pari o molto prossima a zero indica l’assenza di una qualsiasi
interdipendenza tra le due variabili.
Man mano che la correlazione si avvicina a -1 si parla di perfetta correlazione
negativa tra le due variabili: una crescita nella prima comporta un proporzionale
calo nella seconda; e viceversa.
Man mano che la correlazione si avvicina a +1 si parla di perfetta correlazione
positiva: se una variabile cresce, l’altra cresce proporzionalmente.
Dott. Domenico Dall’Olio
[email protected]
21
Variabili continue e variabili discrete
Finanza Aziendale – Bologna – Informatica per il management
Ciascun fenomeno può assumere diversi valori delle variabili.
I fenomeni quantitativi possono presentare un numero finito di valori, o una
infinità numerabile di valori; in tal caso si parla di variabili discrete.
Se il numero di valori che la variabile può assumere è infinito, allora si parla di
variabili continue.
Ogni distribuzione continua può essere convertita in discreta suddividendo i
valori possibili in intervalli, o classi.
Dott. Domenico Dall’Olio
[email protected]
22
La distribuzione Normale
Finanza Aziendale – Bologna – Informatica per il management
La Normale, o Gaussiana, è la più comune distribuzione statistica, per almeno tre ragioni:
1. moltissimi fenomeni seguono almeno approssimativamente tale distribuzione
2. può essere impiegata per approssimare molte distribuzioni di probabilità discrete
3. è la base dell’inferenza statistica, in virtù del teorema centrale del limite
La distribuzione Normale è definita dalla seguente funzione:
1
f ( x) 
e
 2
1  xm 


2  
2
dove m è la media e  (che è sempre positivo) è la deviazione standard.
E’ una funzione sempre positiva, ed è simmetrica rispetto alla sua media: mediana e
media sono quindi coincidenti; il massimo della curva è inversamente proporzionale a .
Dott. Domenico Dall’Olio
[email protected]
23
La distribuzione Normale
Finanza Aziendale – Bologna – Informatica per il management
La forma generica della Normale è la seguente:
L’aspetto più interessante di questa distribuzione è che date la media e la deviazione
standard è possibile calcolare la probabilità di qualsiasi intervallo di valori. In particolare,
all’interno dell’intervallo dato da meno e più una deviazione standard rispetto alla media si
ha il 68.3% di probabilità; salendo a due deviazioni standard si ha il 95.5%, e a tre
deviazioni si ha il 99.7%.
Dott. Domenico Dall’Olio
[email protected]
24
Perchè la Normale è importante in finanza?
Una larga parte dell’ingegneria finanziaria moderna si basa sull’assunto che i rendimenti
Finanza Aziendale – Bologna – Informatica per il management
giornalieri di una qualsiasi serie finanziaria siano distribuiti secondo una Normale, la cui
deviazione standard è pari alla volatilità del titolo in oggetto.
La volatilità gioca quindi un ruolo chiave nella definizione del rischio di un titolo quotato,
dal momento che in funzione del valore di  si possono formare aspettative molto diverse
in materia di rischio. Si osservi infatti la figura seguente:
Dott. Domenico Dall’Olio
[email protected]
25
Perchè la Normale è importante in finanza?
Maggiore la volatilità, maggiore la dispersione dei rendimenti: in tali casi la distribuzione si
Finanza Aziendale – Bologna – Informatica per il management
schiaccia e si allarga.
La conseguenza di ciò è che quando la volatilità è alta è difficile formarsi aspettative
affidabili in tema di rendimento, dato che la probabilità di discostarsi sensibilmente dal
valore atteso è elevata.
Inoltre, quando la volatilità è elevata si ha una maggiore probabilità degli eventi estremi, i
cosiddetti cigni neri, dato che le code della distribuzione sono più sollevate.
In realtà, come vedremo, il modello Normale è soltanto una approssimazione della realtà.
Ora ci occuperemo di definire dei criteri per il formarsi di aspettative ragionate in materia
di rendimento atteso e di rischio atteso in un dato investimento.
Dott. Domenico Dall’Olio
[email protected]
26
Come si determina il rendimento atteso
Finanza Aziendale – Bologna – Informatica per il management
Il rendimento atteso di un investimento può trarre origine da diversi fattori.
In uno studio recente i tre economisti Dimson, Marsh e Staunton hanno misurato la
performance storica di tre diversi portafogli di investimento:
1. un portafoglio di titoli di stato americani a breve termine (i cosiddetti T-Bills)
2. un portafoglio di titoli di stato americani a lungo termine (T-Bonds)
3. un portafoglio di azioni dell’indice Standard & Poor’s 500
Si tratta di tre portafogli dotati di diversi livelli di rischio: i titoli di stato americani a breve
termine possono essere considerati privi di rischio, perché la loro scadenza ravvicinata
rende i prezzi molto stabili; il ritorno reale tuttavia può essere eroso dall’inflazione.
Il secondo portafoglio fluttua con i tassi di interesse; il terzo è soggetto alle fluttuazioni dei
mercati azionari.
Dott. Domenico Dall’Olio
[email protected]
27
Come si determina il rendimento atteso
Il grafico seguente (fonte: Brealey, Myers, Allen) mostra l’andamento dei tre portafogli di
Finanza Aziendale – Bologna – Informatica per il management
cui sopra tra il 1900 e il 2008:
Dott. Domenico Dall’Olio
[email protected]
28
Come si determina il rendimento atteso
Finanza Aziendale – Bologna – Informatica per il management
In termini reali (fonte: Brealey, Myers, Allen):
Dott. Domenico Dall’Olio
[email protected]
29
Come si determina il rendimento atteso
I tre ritorni sono sostanzialmente coerenti con la logica: per i titoli di stato a breve termine,
Finanza Aziendale – Bologna – Informatica per il management
ad esempio, il valore nominale finale di 71 è stato appena sufficiente a coprire l’inflazione,
come emerge osservando il dato in termini reali.
Considerando le serie dei 109 rendimenti dei tre portafogli, divisi per 109, si ottiene il
rendimento medio annuo delle tre tipologie di investimento:
nominale
reale
premio per il
rischio
T-Bills
4.0
1.1
0.0
T-Bonds
5.5
2.6
1.5
Azioni
11.1
8.0
7.1
Si noti che nell’ultima colonna si parla di premio per il rischio: è l’extra-rendimento che si
avrebbe avuto mediamente in funzione di un extra-rischio.
Dott. Domenico Dall’Olio
[email protected]
30
Come si determina il rendimento atteso
Guardare indietro 109 anni potrà apparire strano, ma in effetti non ha senso osservare i
Finanza Aziendale – Bologna – Informatica per il management
rendimenti medi su orizzonti temporali brevi: se ci si focalizzasse sugli ultimi 12 anni, ad
esempio, si avrebbe un rendimento medio negativo su moltissimi mercati, affetti dalle torri
gemelle prima, e dalla crisi globale originata dai mutui sub-prime poi.
Medie calcolate su orizzonti temporali brevi in finanza non hanno alcun senso.
Si noti che il profitto medio annuale del comparto azionario è stato pari al 11.1%; si può
assumere questo valore come aspettativa di rendimento annuale per un investimento
azionario nel 2013? Una simile aspettativa si basa su un assunto molto chiaro: ciò che è
accaduto in passato tenderà a ripetersi nel futuro.
Questo purtroppo NON è l’approccio corretto: il tasso medio di rendimento non è affatto
stabile nel tempo.
Dott. Domenico Dall’Olio
[email protected]
31
La volatilità dei mercati storici
Finanza Aziendale – Bologna – Informatica per il management
Il grafico seguente (fonte: Brealey, Myers e Allen) mostra gli istogrammi dei
rendimenti annuali dei mercati finanziari americani tra il 1900 e il 2008 (gli anni
sono sull’asse orizzontale).
80.0
60.0
40.0
20.0
0.0
-20.0
-40.0
-60.0
Dott. Domenico Dall’Olio
[email protected]
32
Un approccio alternativo
Si osservi la tabella alla slide 29: il rendimento atteso del portafoglio azionario è dato dal
Finanza Aziendale – Bologna – Informatica per il management
rendimento privo di rischio, 4.0% il valor medio storico, più una componente di premio per il
rischio, pari al 7.1% (sempre in termini di valor medio storico).
Ma il tasso privo di rischio cambia sensibilmente nel tempo. Negli anni ’80 del secolo scorso, ad
esempio, i tassi americani a breve termine erano intorno al 15%. In un simile periodo nessuno
avrebbe accettato un ritorno del 11.1% da un investimento azionario, cioè rischioso, quando
poteva avere il 15% a rischio pressoché nullo!
Un metodo più ragionato potrebbe quindi consistere nel sommare il premio per il rischio medio
storico al tasso corrente dei titoli privi di rischio. In questo modo il rendimento atteso dai titoli
azionari negli anni ‘80 sarebbe stato del 22.1%.
Questo approccio è apprezzato da molti operatori, ma aspramente criticato da altrettanti.
La critica principale è che in genere il mercato si aspetta premi per il rischio molto minori di
quello medio indicato dal modello storico.
Dott. Domenico Dall’Olio
[email protected]
33
Il rischio Paese
Finanza Aziendale – Bologna – Informatica per il management
Un aspetto importante del rischio dell’investimento azionario è che esso viene
percepito su diversi livelli in funzione del Paese in cui le azioni sono quotate. Il
grafico seguente (fonte: Brealey, Myers, Allen) mostra i premi per il rischio medi
di diversi Paesi del mondo.
Dott. Domenico Dall’Olio
[email protected]
34
Un altro metodo per stimare I rendimenti attesi
Finanza Aziendale – Bologna – Informatica per il management
Il premio per il rischio può essere determinato in modo alternativo considerando
il cosiddetto modello di crescita costante dei dividendi.
Se i prezzi dei titoli quotati tengono il passo della crescita dei dividendi, allora il
ritorno atteso di mercato è pari al tasso di dividendo sommato al tasso di
crescita dei dividendi stessi.
I tassi di dividendo negli USA hanno avuto valori medi intorno al 4.3% tra il 1900
e il 2008, e la crescita media annuale dei dividendi è stata pari al 5.3%. Dunque
il rendimento atteso del mercato sarebbe stato del 9.6%, 5.6 punti al di sopra
del tasso di interesse privo di rischio.
Anche questo metodo trova sostenitori e detrattori, in virtù della estrema
volatilità dei dati osservati (vedi slide successiva).
Dott. Domenico Dall’Olio
[email protected]
35
Un altro metodo per stimare I rendimenti attesi
di dividendo negli USA nel periodo tra il 1900 e il 2008:
10.00
9.00
8.00
Dividend Yield (%)
7.00
6.00
5.00
4.00
3.00
2.00
1.00
Dott. Domenico Dall’Olio
[email protected]
2005
2000
1995
1990
1985
1980
1975
1970
1965
1960
1955
1950
1945
1940
1935
1930
1925
1920
1915
1910
1905
0.00
1900
Finanza Aziendale – Bologna – Informatica per il management
Il grafico seguente (fonte: Brealey, Myers e Allen) mostra l’andamento dei tassi
36
L’errore di stima nell’utilizzo di dati storici
Finanza Aziendale – Bologna – Informatica per il management
Torniamo al modello basato sui rendimenti storici dei tre portafogli. Nell’utilizzo
di dati storici per definire aspettative di rendimento futuro bisogna essere pronti
al rischio di errore, che può essere misurato in termini di varianza o di
deviazione standard.
Le deviazioni standard e le varianze osservate sui tre portafogli nel periodo
1900-2008 sono alla tabella seguente (fonte: Brealey, Myers, Allen):
Dott. Domenico Dall’Olio
[email protected]
dev. st.
varianza
T-Bills
2.8
7.7
T-Bonds
8.3
69.3
Azioni
20.2
406.4
37
L’importanza della geografia
Finanza Aziendale – Bologna – Informatica per il management
Di nuovo il Paese a cui appartiene il mercato azionario su cui si investe gioca un
ruolo chiave nella definizione dei livelli di rischio e di rendimento, come emerge
dalla figura seguente (fonte: Brealey, Myers e Allen):
Dott. Domenico Dall’Olio
[email protected]
38
Come la diversificazione riduce il rischio
Si osservi la tabella seguente (fonte: Brealey, Myers, Allen), che mostra le deviazioni
Finanza Aziendale – Bologna – Informatica per il management
standard di alcuni titoli di diversi Paesi in un quinquennio recente (2004-2008), confrontate
con quelle dei rispettivi mercati di appartenenza:
dev. st.
Azione
dev. st.
azione
mercato
Azione
azione
mercato
BP
20.7
16.0
LVMH
20.6
18.3
Deutsche Bank
28.9
20.6
Nestlè
14.6
13.7
Fiat
35.7
18.9
Nokia
31.6
25.8
Heineken
21.0
20.8
Sony
33.9
16.6
Iberia
35.4
20.4
Telefonica
58.6
40.0
Una domanda cruciale sorge spontanea: se gli indici di mercato sono composti di singole
azioni perché allora la loro volatilità non riflette quella dei rispettivi componenti? La
risposta è che la diversificazione riduce la volatilità (e quindi il rischio).
Dott. Domenico Dall’Olio
[email protected]
39
Perchè la diversificazione riduce il rischio
Finanza Aziendale – Bologna – Informatica per il management
Cerchiamo di capire il problema in termini concettuali prima di affrontarlo in termini matematici.
Un portafoglio di azioni, come un indice ad esempio, è un paniere di titoli che a meno di casi
sporadici (di breve periodo) non salgono e non scendono tutti insieme, né tantomeno con la
stessa intensità.
Come conseguenza delle diverse volatilità e delle correlazioni tra coppie, che in alcuni casi
saranno positive, in altri negative, in altri ancora nulle, il risultato globale è un portafoglio che
dovrebbe performare come la media dei titoli che lo compongono in termini di rendimento, e al
di sotto della media dei componenti in termini di volatilità dei rendimenti.
Gli americani dicono “l’alta marea solleva tutte le barche”; non tutte nello stesso modo però.
Gli andamenti e le volatilità dei vari componenti tendono a compensarsi a vicenda, la maggior
parte delle volte: i prezzi non si muovono esattamente nello stesso modo in ogni istante di
tempo.
Dott. Domenico Dall’Olio
[email protected]
40
Tipologie di rischio
Finanza Aziendale – Bologna – Informatica per il management
Il punto focale è che vi sono due tipologie di rischio insite in ogni titolo quotato.
La prima è strettamente collegata al titolo stesso e alla capacità dei manager di creare valore
per l’impresa, investendo in progetti che valgono più dei rispettivi costi. Questo è il cosiddetto
rischio specifico.
Detto anche rischio unico, è legato a fattori che incidono soltanto sui risultati di quella azienda
(e dei diretti concorrenti). Viene detto anche rischio diversificabile: è il rischio che può essere
ridotto grazie alla diversificazione, ossia all’investimento su più titoli anziché su uno soltanto.
La seconda sorgente di rischio è legata al mercato totale: quando il mercato sale, più o meno
tutte le azioni in esso comprese salgono, e viceversa. In altre parole, accade spesso che i
movimenti di prezzo di un titolo non dipendano da fattori legati al titolo stesso, bensì dal fatto
che tutti gli altri titoli si stanno muovendo.
Questo rischio viene detto sistematico, o non diversificabile: non esiste un solo titolo che possa
essere svincolato dall’andamento globale del mercato.
Dott. Domenico Dall’Olio
[email protected]
41
Un semplice esempio
Si osservi cosa succede combinando due sole azioni, suddividendo su di esse in modo
Finanza Aziendale – Bologna – Informatica per il management
equivalente un capitale di 100$:
(fonte: Brealey, Myers, Allen)
La diversificazione (linea blu) riduce la volatilità dei rendimenti, rendendo più dolce
l’andamento del portafoglio.
Dott. Domenico Dall’Olio
[email protected]
42
Finanza Aziendale – Bologna – Informatica per il management
Gli effetti della diversificazione
fonte: Brealey, Myers, Allen
Dott. Domenico Dall’Olio
[email protected]
43
Gli effetti della diversificazione
Finanza Aziendale – Bologna – Informatica per il management
Il rischio di un portafoglio non può essere annullato, ma drasticamente ridotto,
grazie alla diversificazione, fino ad un limite asintotico, pari al rischio di mercato.
Non è possibile trovare combinazioni di titoli dotate di livelli di rischio minori di
quello del mercato globale.
Ciò perché il rischio eliminabile è soltanto quello specifico: il rischio sistematico
non è evitabile in alcun modo.
Un aspetto importante della diversificazione è che non è necessario includere in
portafoglio decine o centinaia di titoli: già dopo 8-10 titoli il rischio converge a
quello di mercato, e il contributo di ogni titolo aggiuntivo è marginale.
Dott. Domenico Dall’Olio
[email protected]
44
Come si calcola il rischio di portafoglio
Finanza Aziendale – Bologna – Informatica per il management
Ora vedremo di capire come il rischio di un portafoglio dipenda dal rischio di un singolo titolo.
Si supponga che il 60% del proprio portafoglio sia investito in azioni McDonald’s e che il
restante 40% sia in azioni Microsoft. Fatto 3.1% il rendimento atteso dal primo e 9.5% quello del
secondo, il rendimento globale atteso è dato dalla media ponderata dei due rendimenti:
E (r )  (0.6 * 3.1%)  (0.4 * 9.5%)  5.7%
Siano 15.8% e 23.7% le rispettive deviazioni standard passate, e si assuma che esse possano
essere considerate una buona misura del loro valore futuro. Se il rischio globale fosse il rischio
medio ponderato, allora si avrebbe:
E ( )  (0.6 *15.8%)  (0.4 * 23.7%)  19.0%
Ma in realtà ciò si verifica soltanto se le due azioni si muovono perfettamente insieme, ossia se
sono perfettamente correlate.
Dott. Domenico Dall’Olio
[email protected]
45
Calcolo della volatilità di portafoglio
Il calcolo corretto della volatilità totale di un portafoglio di due titoli consiste nel sommare tutte le
Finanza Aziendale – Bologna – Informatica per il management
celle della seguente matrice:
Stock 1
Stock 1
Stock 2
xσ
2
1
2
1
Stock 2
x 1x 2σ 12 
x 1x 2σ 12 
x 1x 2ρ 12σ 1σ 2
x 1x 2ρ 12σ 1σ 2
x 22σ 22
nella quale i fattori xi sono i pesi dei singoli titoli in portafoglio, e infine nel calcolare la radice
quadrata della quantità trovata. A parole, la varianza totale del portafoglio è la somma delle due
varianze ponderate sui quadrati dei pesi e delle due covarianze ponderate sui prodotti dei pesi.
La volatilità totale è la radice quadrata della varianza totale.
Dott. Domenico Dall’Olio
[email protected]
46
Calcolo della volatilità di portafoglio
Secondo il procedimento appena illustrato, il rischio globale di portafoglio è determinato dalla
Finanza Aziendale – Bologna – Informatica per il management
sommatoria delle componenti di rischio specifico dei singoli titoli ponderate sui rispettivi pesi, più
la componente di rischio sistematico insita nel grado di covarianza esistente tra i titoli inclusi in
portafoglio.
Si noti che la covarianza qui è espressa in funzione della correlazione: è soltanto un modo
molto più rapido per calcolare la covarianza, rispetto all’applicazione della sua formula standard.
Anche la covarianza va ponderata, e siccome i titoli sono due va ponderata sul prodotto dei
rispettivi pesi.
Dott. Domenico Dall’Olio
[email protected]
47
Casi particolari
Finanza Aziendale – Bologna – Informatica per il management
1. Perfetta correlazione positiva tra i due titoli:
12  1  VAR( P)  x12 12  2 x1 x2 1 2  x22 22  ( x1 1  x2 2 ) 2
st.dev( P)  x1 1  x2 2
In tal caso la volatilità di portafoglio è la media ponderata delle singole volatilità.
2. Assenza di correlazione tra i due titoli:
12  0  VAR( P)  x12 12  x22 22
In tal caso la varianza di portafoglio è la media ponderata delle singole varianze.
3. Perfetta correlazione negativa tra i due titoli:
12  1  VAR( P)  x12 12  2 x1 x2 1 2  x22 22  ( x1 1  x2 2 ) 2
st.dev( P)  x1 1  x2 2
In un simile caso sarebbe idealmente possibile individuare una combinazione di due azioni che
azzera il rischio. Nella realtà la perfetta correlazione negativa non si verifica mai.
Dott. Domenico Dall’Olio
[email protected]
48
Casi particolari
Ritorniamo ai dati di McDonald’s e Microsoft. Se vi fosse perfetta correlazione positiva tra i due
Finanza Aziendale – Bologna – Informatica per il management
titoli la volatilità totale di portafoglio sarebbe la seguente:
 P2  0.62 15.82  0.42  23.7 2  2  0.6  0.4 115.8  23.7  359.5
st.dev( P)  359.5  19%
cioè il valore che ci aspettavamo: la media ponderata delle due volatilità specifiche.
Se la correlazione vera è pari a 0.18, allora la volatilità di portafoglio si riduce sensibilmente:
 P2  0.62 15.82  0.42  23.7 2  2  0.6  0.4  0.18 15.8  23.7  212.1
st.dev( P)  212.1  14.6%
Si noti che il rischio globale è minore del minore dei due rischi specifici: è l’effetto principale
della diversificazione.
Dott. Domenico Dall’Olio
[email protected]
49
Rischio asintotico di portafoglio
Dato un portafoglio di N titoli, la matrice delle varianze e covarianze ponderate contiene NxN
Finanza Aziendale – Bologna – Informatica per il management
termini, di cui N termini di varianza e N2-N termini di covarianza. Sommando tutti i termini si
giunge alla varianza totale di portafoglio. La radice quadrata di questa quantità porta infine alla
volatilità (cioè al rischio) di portafoglio.
Più si aggiungono titoli al portafoglio, più le covarianze diventano importanti: maggiore N,
maggiore il numero delle covarianze. Si immagini dunque di dividere un portafoglio in N azioni
di pari peso, 1/N. In tal caso la varianza totale di portafoglio è pari a:
2
1
 1  1  2
2
2
VAR( P)  N     i  N  N      ij
N
 N  N 
1
1 2

2
   i  1     ij
N
 N
Se N tende all’infinito, la varianza totale tende alla covarianza media: è ciò che rimane dopo il
lavoro di diversificazione. Il rischio specifico scompare e rimane solo quello sistematico!
Dott. Domenico Dall’Olio
[email protected]
50
La sensitività di una azione al mercato: Beta
Il risultato fondamentale emerso alla slide precedente è che il rischio di un portafoglio ben
Finanza Aziendale – Bologna – Informatica per il management
diversificato dipende dal rischio di mercato delle azioni incluse nel portafoglio stesso.
Il punto focale è che nella costruzione di un portafoglio non importa tanto quanto una
azione sia rischiosa se presa da sola, ma quanto essa concorra al rischio totale di
portafoglio. Questa sensitività del titolo rischio di mercato dipende dalla componente di
rischio sistematico del titolo stesso, cioè da quanto quel titolo sia sensibile alle variazioni
di prezzo del mercato globale.
Questa sensitività è chiamata Beta (b)
Titoli con Beta maggiori di 1 tendono ad amplificare il movimento globale del mercato;
titoli con Beta compreso tra 0 e 1 tendono a muoversi nella stessa direzione del mercato,
ma con minore intensità.
Il mercato globale ha ovviamente Beta pari a 1.
Dott. Domenico Dall’Olio
[email protected]
51
Come si calcola il Beta
Finanza Aziendale – Bologna – Informatica per il management
Il Beta è dato dalla formula seguente:
 im
bi  2
m
A parole, il Beta del titolo i-esimo è pari alla covarianza tra il titolo i-esimo e il mercato
divisa per la varianza del mercato: si rapporta la componente di rischio sistematico del
titolo al rischio sistematico dell’intero mercato.
Il Beta misura il contributo del titolo i-esimo al rischio di portafoglio.
Il Beta di un portafoglio è la media ponderata dei Beta dei singoli componenti.
Dott. Domenico Dall’Olio
[email protected]
52
Finanza Aziendale – Bologna – Informatica per il management
Esercizio 1
Dati il titolo A con una volatilità del 25%, il titolo B con una volatilità del 40% e un
coefficiente di correlazione tra i due pari a 0.2, si calcoli il rischio totale del
portafoglio nel quale il titolo B pesa un terzo del titolo A.
Esercizio 2
Si consideri il seguente portafoglio di tre titoli:
Titolo
A
B
C
r atteso
5.8%
6.8%
8.0%
s.q.m.
7%
9%
12%
Sul titolo A è stato investito un quinto del denaro a disposizione; il rendimento
atteso globale del portafoglio è il 7%. Determinare i pesi dei titoli B e C.
Determinare poi la volatilità totale di portafoglio, date le correlazioni seguenti:
corr(A,B)=0.67, corr(B,C)= 0.55, corr(A,C)=0.28
Dott. Domenico Dall’Olio
[email protected]
53
Finanza Aziendale – Bologna – Informatica per il management
Esercizio 3
Considerate un portfafoglio fatto di 10 azioni equamente pesate. Tre di loro
hanno un sigma pari a 25 e un beta pari a 0,8, le altre sette hanno un
sigma pari a 30 e un beta pari a 1,15. La correlazione tra le prime tre azioni
è 0,3, quella tra le altre sette è 0,2; la correlazione tra i due gruppi è infine
0,6. Risolvete i seguenti problemi:
•
determinate la volatilità totale di portafoglio
•
supponete di cambiare le quote di capitale investite nei 10 titoli: 500mila
euro su ciascuno dei primi tre e 275mila euro su ciascuno dei rimanenti
sette; quanto vale il beta di portafoglio?
Esercizio 4
Il titolo Fiat ha un rendimento atteso del 35% con un rischio del 25%; il titolo
Generali ha un rendimento atteso del 19% con un rischio del 7%.
Assumendo tra i due una correlazione pari a 0,15, si determinino il
rendimento atteso e la volatilità attesa del portafoglio nel quale il titolo Fiat
incide il 25%.
Dott. Domenico Dall’Olio
[email protected]
54
Finanza Aziendale – Bologna – Informatica per il management
Esercizio 5
Un portafoglio è costituito dai due titoli A e B. Il rendimento atteso di A è il 10%,
con volatilità dell’8%; il rendimento atteso di B è il 30%, con volatilità del 38%.
Si scelgano i pesi dei due titoli in modo che il rendimento atteso del portafoglio
sia pari al 16%.
Si calcoli quindi il rischio del portafoglio così costituito, assumendo un indice di
correlazione tra i due titoli pari a 0,15.
Esercizio 6
Il titolo Microsoft ha un rendimento atteso del 35% con un rischio del 49%; il
titolo Mc Donald’s ha un rendimento atteso del 19% con un rischio del 27%.
Assumendo tra i due una correlazione pari a 0,34, si determinino il rendimento
atteso e la volatilità attesa del portafoglio nel quale il titolo Mc Donald’s incide il
75%.
Dott. Domenico Dall’Olio
[email protected]
55
Un passo avanti
Finanza Aziendale – Bologna – Informatica per il management
La teoria della diversificazione come metodo per ridurre il rischio di portafoglio
risale ad un articolo del 1952 di Harry Markovitz; in esso l’autore mostrò come
un investitore potesse ridurre il rischio di portafoglio combinando tra loro azioni
che non si muovono esattamente nello stesso modo.
Ma come vanno scelte le azioni specifiche?
Il passo successivo consiste nel determinare se esistano dei criteri migliori di
altri per la costruzione del portafoglio.
Ora dobbiamo quindi risolvere due problemi: il primo è come si possano
scegliere le azioni da mettere in portafoglio, e in quali proporzioni; il secondo è
come un investitore possa formarsi aspettative ragionevoli in termini di rischio e
rendimento.
Dott. Domenico Dall’Olio
[email protected]
56
Rendimenti attesi: analisi storica di un titolo
Il grafico seguente (fonte: Brealey, Myers, Allen) mostra i rendimenti giornalieri del titolo IBM nel
intervalli di tempo relativamente brevi i rendimenti giornalieri seguono una distribuzione affine
alla gaussiana.
4.0
3.5
Percentuale di giorni
Finanza Aziendale – Bologna – Informatica per il management
decennio 1998-2008, a cui è sovrapposta una campana gaussiana. Come si può notare, su
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
rendimento giornaliero
Dott. Domenico Dall’Olio
[email protected]
57
Confronto tra titoli (fonte: Brealey, Myers, Allen)
20
20
A
18
% probabilità
Finanza Aziendale – Bologna – Informatica per il management
16
18
16
14
14
12
B
12
10
10
8
8
6
4
6
2
4
2
0
-50
0
50
0
-50
0
50
% rendimento
20
18
Meglio A o B?
A or C?
B or C?
16
C
14
12
10
8
6
4
2
0
Dott. Domenico Dall’Olio
[email protected]
-50
0
50
58
Scegliere i titoli
Finanza Aziendale – Bologna – Informatica per il management
Torniamo all’esempio di McDonald’s e Microsoft. Il secondo titolo è attraente in
termini di rendimento atteso, ma presenta un livello di rischio superiore al primo.
La combinazione dei due titoli può essere effettuata idealmente in un numero
infinito di possibilità, dato che la proporzione di ciascun titolo può spaziare su
qualsiasi valore compreso tra 0 e 100.
Nell’esempio visto in precedenza avevamo combinato il 60% di capitale sul
titolo McDonald’s e il restante 40% sul titolo Microsoft, ottenendo un ritorno
atteso del 5.7% e un rischio atteso del 14.6%.
E se avessimo combinato i due titoli in modo diverso?
Dott. Domenico Dall’Olio
[email protected]
59
Gli effetti di diverse combinazioni dei titoli
Microsoft
Rendimento atteso (%)
Finanza Aziendale – Bologna – Informatica per il management
Ogni combinazione dei due titoli è un punto sulla seguente curva:
40% in Microsoft
60% in McDonald’s
McDonald’s
Deviazione standard
Dott. Domenico Dall’Olio
[email protected]
60
Considerazioni sui portafogli
Finanza Aziendale – Bologna – Informatica per il management
In linea teorica non esiste una combinazione migliore di altre: dipende per lo più
dal livello di tolleranza al rischio dell’investitore.
Un dubbio però dovrebbe insorgere: la curva in figura precedente è formata da
tutte le possibili combinazioni dei due titoli McDonald’s e Microsoft; ma quelle
combinazioni hanno tutte senso? O piuttosto alcune sono irragionevoli?
In effetti non tutte le combinazioni sono ragionevoli: qualsiasi combinazione
rappresentata da un punto nella parte inferiore della curva offre ritorni inferiori
rispetto ad altre combinazioni di pari rischio.
Nessun investitore razionale metterebbe mai consapevolmente i propri soldi in
simili portafogli.
Dott. Domenico Dall’Olio
[email protected]
61
Complichiamo il modello
Finanza Aziendale – Bologna – Informatica per il management
Si osservi ora la tabella seguente (fonte: Brealey, Myers, Allen), che riporta i dati
di 10 titoli e di alcune loro specifiche combinazioni:
Dott. Domenico Dall’Olio
[email protected]
62
Lo spazio di tutti i portafogli possibili
Finanza Aziendale – Bologna – Informatica per il management
Combinando due o più titoli, fino a dieci, dalla lista in tabella precedente si può
ottenere ciascun punto dell’area verde del grafico seguente (fonte: Brealey,
Myers, Allen):
Dott. Domenico Dall’Olio
[email protected]
63
La frontiera efficiente
Finanza Aziendale – Bologna – Informatica per il management
Ciascun quadratino in figura precedente è uno dei dieci titoli dell’elenco, mentre
ogni punto dell’area verde è una possibile combinazione di due o più di essi.
Una domanda importantissima ora: in quale direzione è più ragionevole tentare
di spostarsi?
La risposta è immediata: in alto e a sinistra. Maggiori ritorni con minori rischi!
Qual è il limite? Il limite è dato dalla linea esterna dell’area verde, che viene
definita frontiera efficiente.
Ogni punto sulla frontiera efficiente è il miglior portafoglio possibile in termini di
rendimento ponderato sul rischio: nessun altro portafoglio è in grado di offrire un
miglior rendimento a parità di rischio, o ridurre il rischio a parità di rendimento.
Dott. Domenico Dall’Olio
[email protected]
64
Complichiamo il modello
Finanza Aziendale – Bologna – Informatica per il management
Ora introduciamo una nuova componente al modello: la possibilità di prestare o
di prendere in prestito denaro:
Expected Return (%)
S
rf
T
Fonte: Brealey, Myers, Allen
Dott. Domenico Dall’Olio
[email protected]
Standard Deviation
65
Complichiamo il modello
Finanza Aziendale – Bologna – Informatica per il management
Supponiamo che il denaro possa essere prestato e preso a prestito allo stesso
tasso di interesse, rf.
Grazie ai prestiti di denaro (in un senso o nell’altro) possiamo spostarci al di
fuori della frontiera efficiente.
Investendo una parte del denaro in titoli di stato a breve termine, ad esempio,
cioè prestando denaro, e investendo il capitale residuo nel portafoglio S (vedi
slide precedente) di azioni si possono ottenere combinazioni di rischio e di
rendimento lungo la linea che collega rf ad S.
Se invece si prende a prestito denaro, allora ci si può muovere sui punti della
linea a destra del portafoglio S.
Dott. Domenico Dall’Olio
[email protected]
66
Il miglior portafoglio efficiente e l’indice di Sharpe
A prescindere dal livello di rischio prescelto, è sempre possibile dunque ottenere il
Finanza Aziendale – Bologna – Informatica per il management
massimo rendimento atteso combinando il portafoglio S con un prestito di denaro.
Il portafoglio S viene detto miglior portafoglio efficiente.
Per individuare il portafoglio S è sufficiente cercare la linea che trae origine dal punto rf e
che risulta tangente alla frontiera efficiente nel punto più alto possibile. Il portafoglio S si
trova nel punto di tangenza.
Il portafoglio S è dotato del miglior rapporto di premio al rischio su deviazione standard;
questo rapporto viene definito indice di Sharpe:
r  rf
risk premium
Sharpe ratio 

standard deviation

Dott. Domenico Dall’Olio
[email protected]
67
La natura del miglior portafoglio efficiente
Per capire quale possa essere la composizione del miglior portafoglio efficiente bisogna
Finanza Aziendale – Bologna – Informatica per il management
ragionare in termini di pubblicità delle informazioni.
Se fosse possibile avere sempre accesso alle informazioni migliori, allora sarebbe sempre
possibile estrapolare dal mercato le azioni in grado di offrire i rendimenti più elevati.
In una situazione di mercato competitiva, il monopolio delle buone informazioni non è
ragionevolmente perseguibile, perciò in linea di massima le informazioni sono equamente
distribuite sul mercato.
In un simile caso non c’è motivo di investire in un portafoglio diverso da quello di mercato,
che dunque risulta essere il miglior portafoglio efficiente.
In altri termini, ciò che il modello suggerisce è che la gestione attiva del proprio denaro è
penalizzante nel lungo periodo, metre l’unica gestione sensata è quella passiva.
Dott. Domenico Dall’Olio
[email protected]
68
La relazione tra rischio e rendimento
Finanza Aziendale – Bologna – Informatica per il management
Si riprenda ora il grafico che mette in relazione il rischio e il rendimento dei vari
portafogli possibili (fonte: Brealey, Myers, Allen):
rendimento
Rend. del mercato rm
Portafoglio di mercato
tasso privo di
rischio
rf
rischio
Dott. Domenico Dall’Olio
[email protected]
69
Una nuova lettura
Finanza Aziendale – Bologna – Informatica per il management
E ora si sostituisca il rischio con il Beta:
rendimento
Rend. del mercato rm
Portafoglio di mercato
tasso privo di
rischio
rf
1.0
Dott. Domenico Dall’Olio
[email protected]
b
beta
70
Il Capital Asset Pricing Model
I titoli di stato, a beta nullo, non hanno alcun premio per il rischio e rendono il tasso privo di
Finanza Aziendale – Bologna – Informatica per il management
rischio, rf.
Il portafoglio di mercato ha beta 1 e rende rm. Il premio per il rischio è quindi pari a (rm – rf ).
Cosa succede a tutti gli altri portafogli? La risposta l’hanno data Sharpe, Lintner e Treynor nel
1960: il premio per il rischio atteso è direttamente proporzionale al Beta.
Questa teoria è nota come Capital Asset Pricing Model (CAPM).
La linea retta sul grafico viene definita Security Market Line (SML) e ci dice che un portafoglio
dotato di un Beta pari a 0.5 ha un rischio pari a metà del rischio del portafoglio di mercato,
mentre un portafoglio dotato di Beta pari a 2 ha un rischio doppio di quello di mercato; e così
via. In formule:
r  rf  b  (rm  rf )
Dott. Domenico Dall’Olio
[email protected]
71
La Security Market Line
Finanza Aziendale – Bologna – Informatica per il management
La retta del CAPM può essere vista come la retta di equilibrio tra rischio e
rendimento: ogni punto di essa rappresenta un punto di ottimo, nel quale il
rendimento atteso è sempre coerente con il rischio atteso, misurato dal Beta.
La SML può essere utilizzata per verificare se un titolo è sopra o sottovalutato:
qualsiasi titolo si trovi al di sopra della SML, infatti, offre un rendimento atteso
maggiore di quello che dovrebbe, dunque è sottovalutato (cioè quota un prezzo
di mercato inferiore a quello che dovrebbe avere).
Né allo stesso tempo, qualsiasi titolo può trovarsi sotto la SML, perché in tal
caso offrirebbe un rendimento atteso minore di quello di equilibrio, dunque
sarebbe sopravvalutato (il prezzo di mercato sarebbe superiore a quello che
dovrebbe avere).
Dott. Domenico Dall’Olio
[email protected]
72
Limiti del CAPM
Finanza Aziendale – Bologna – Informatica per il management
Il CAPM va preso per quello che è: un modello che tenta di spiegare in termini
semplici un mondo estremamente complesso.
Alcuni studi lo hanno messo sul banco di prova, dimostrando come esso possa
descrivere la realtà dei mercati soltanto in alcuni momenti di mercato.
Del resto il CAPM si basa su alcune ipotesi poco realistiche:
- il rischio dei titoli di stato è molto basso, ma non nullo;
- non considera l’effetto dell’inflazione;
- il tasso a cui gli investitori possono prestare e prendere a prestito denaro non
è mai lo stesso.
Dott. Domenico Dall’Olio
[email protected]
73
Esercizio 7
Finanza Aziendale – Bologna – Informatica per il management
Dati i seguenti titoli e i rispettivi beta:
Titolo
Fiat
Mediaset
Atlantia
Generali
Beta
1.35
1.65
0.32
0.83
Assumendo che valga il CAPM, che il tasso privo di rischio sia il 3,5% e il
premio per il rischio di mercato sia pari al 15%, si determinino i rendimenti attesi
dei quattro titoli.
Si calcoli poi il tasso di rendimento atteso del portafoglio nel quale Fiat pesa il
15%, Mediaset pesa il 13% e Atlantia pesa tre volte Generali.
Dott. Domenico Dall’Olio
[email protected]
74
Finanza Aziendale – Bologna – Informatica per il management
Esercizio 8
Date le seguenti informazioni relative al mercato ed ai titoli azionari indicati,
verificare quali di essi presentano una valutazione in linea con il CAPM, ed
indicare eventuali sopra o sottovalutazioni:
R(M)=10%
Titolo
A
B
C
D
E
F
G
H
I
Dott. Domenico Dall’Olio
[email protected]
varianza=6%
Beta
0.2
1.5
0.9
0.18
1.2
0.75
0.6
1.1
0.56
tasso risk free=4%
r atteso
5%
10%
13%
6%
12%
8.5%
9%
10%
8%
75