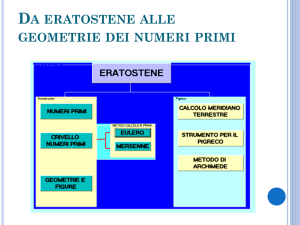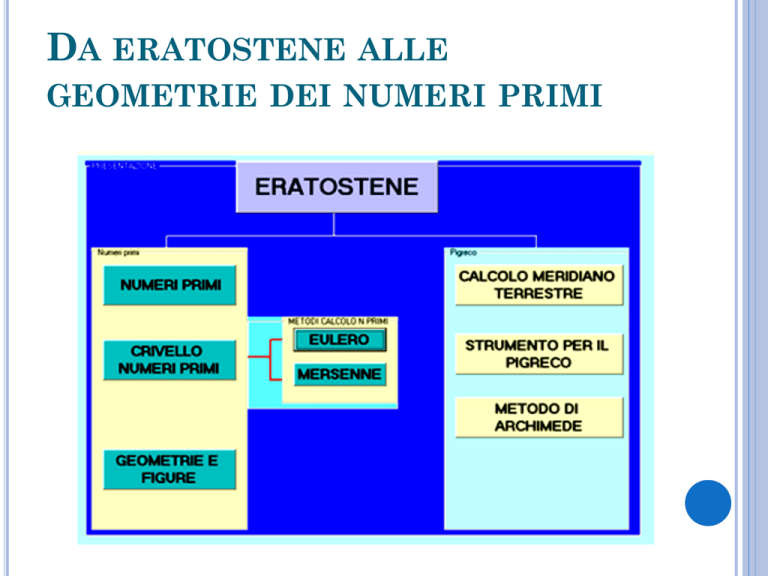
DA ERATOSTENE ALLE
GEOMETRIE DEI NUMERI PRIMI
Eratostene di Cirene
Eratostene, nato a Cirene nel 275 a.C. e morto ad Alessandria d’Egitto nel 195
a.C., è stato un matematico, astronomo, geografo e poeta greco antico.
Fu uno degli intellettuali più versatili della sua epoca ed oggi è soprattutto
ricordato per aver misurato per primo, con grande precisione, le dimensioni della
Terra e, in particolare, del meridiano terrestre passante per Alessandria d’Egitto.
Tra i risultati matematici di Eratostene, quello più noto è il crivello di Eratostene,
un metodo per individuare i numeri primi.
MERIDIANO TERRESTRE: un arco immaginario che congiunge il Polo Nord
terrestre con il Polo Sud.
NUMERO PRIMO: in matematica, un numero primo è un numero naturale
maggiore di 1 che sia divisibile unicamente per 1 e per se stesso; al
contrario, un numero maggiore di 1 che abbia più di due divisori è
detto composto.
Euclide negli Elementi riporta alcuni risultati fondamentali:
• I Teorema : Esistono infiniti numeri primi
• II Teorema: Ogni numero non primo può scomporsi nel prodotto
di più numeri primi e questa scomposizione è unica.
Il crivello di Eratostene
Il metodo trae origine dalla necessità di
concretizzare i numeri naturali con dei
“sassolini” , facendoli passare attraverso
un setaccio o crivello.
CRIVELLO DI ERATOSTENE: Il crivello, o setaccio, di Eratostene è un
antico procedimento, ideato dallo stesso Eratostene, per il calcolo delle
tabelle di numeri primi fino ad un certo numero n prefissato.
Data la sua semplicità di traduzione in un qualsiasi linguaggio di
programmazione, è ancora utilizzato come *algoritmo di calcolo dei
numeri primi da molti programmi per computer.
Trattando
l’anticrivello abbiamo notato
delle simmetrie e regolarità anche
piacevoli.
Possiamo
allora produrre figure
combinando numeri primi mediante una
trasformazione particolare.
EULERO E MERSENNE
NUMERO DI MERSENNE PIU’
GRANDE
43.112.609
N= 2
=
-1
316470269…………….697152511
Cifre=12. 978.189
Data scoperta = 23 agosto 2008 GIMPS
Edson Smith, George Woltman
Da quanto abbiamo visto possiamo
concludere che:
sappiamo ancora molto poco sui numeri primi.
In particolare:
Non si conosce una formula che permetta di
generare i numeri primi.
La distribuzione dei numeri primi sembra a
prima vista casuale.
Sono frequenti i numeri primi gemelli cioè
accoppiati a distanza di 2.
VANTAGGI
Il
fatto di sapere così poco sui numeri
primi si è rivelato un vantaggio per la
crittologia; oggi quasi tutti i computer
usano per comunicare in modo riservato il
cifrario RSA (indica un algoritmo di
crittografia asimmetrica) basato appunto
sulla difficoltà di scomporre in fattori
primi numeri molto grandi (centinaia di
cifre).
TRASFORMAZIONE
Consideriamo la seguente Trasformazione costituita da
quattro traslazioni:
. verso sinistra
. verso l’ alto
. verso destra
. verso il basso
Queste 4 traslazioni formano, per noi, 1 crivello.
METODO OPERATIVO.
1) Prendiamo per esempio 3 numeri primi e i loro multipli :
.
3
6
5
10
7
14
9
15
.
12
.
.
2) Li raccogliamo in un insieme in ordine crescente:
3,5,6,7,9,10,12,14..
3) Consideriamo gli spazi che si creano tra un numero
e l’altro
3,5,6,7,9,10,12,14..
Es.
Tra il 3 e il 5 ci sono 2 spazi quindi la
distanza è d=5-3=2
VEDIAMO LA FIGURA CHE SI FORMA USANDO
CRIVELLI (OVVERO 6 TRASLAZIONI)
CON I MULTIPLI DI: 3, 5, 7
Notiamo che dal
10 al 12 ci sono
2 unità verso
l’ alto. Dato che
d=12 – 10 = 2.
1,5
3,5,6,7,9,10,12,14.
12
7
6
3
5
9
10
VAI AL
METODO
Il metodo di Eratostene per la misura del raggio terrestre
Distanza Alessandria-Siene= 800 km
a =1/50 *360°
(angolo giro)
Applicando la proporzione arco(AS) : Circ. = a : 360°
Circ.= arco(AS) *360°: a = 800*360*50:360 = 40.000 km
La circonferenza reale all’equatore è di 40.009 km
con un errore di 9 km.
STRUMENTO PER
IL CALCOLO DEL PI-GRECO
CALCOLO DEL PI-GRECO
Mediante lo strumento
p
(cerchio in legno )
Consideriamo un cerchio di raggio r = 360 mm ed imponiamo,
mediante una proporzione, il legame tra la circonferenza e l’arco (OA):
Il problema adesso è misurare l’arco OA. Questo risulta possibile
mediante la sua rettificazione .
Archimede di Siracusa
Archimede, nato a Siracusa nel 287 a.C. circa e
morto nella medesima città attorno al 212 a.C.,
fu un matematico, ingegnere, fisico e inventore
greco antico. Fu senza dubbio uno dei più
importanti scienziati di tutta la storia.
Archimede in un dipinto di
Domenico Fetti, 1620
Non abbiamo molte notizie certe sulla sua vita, tramandateci
perlopiù da storici greci, quali Polibio e Plutarco, e romani, come Tito
Livio.
Calcolo di π secondo Archimede
Diverse approssimazioni di π erano già state fatte dai Babilonesi,
dagli Egiziani ed anche dai Cinesi, ma il metodo utilizzato da
Archimede è nuovo perché è un processo iterativo, in quanto si
può trovare un’approssimazione accurata quanto più lo si
desidera semplicemente ripetendo il processo, usando le
precedenti stime di π per ottenerne di nuove.
Egli riconobbe che il rapporto fra la circonferenza e il suo
diametro è sempre costante uguale a 3.14…
C = 2*π*r
π = C/(2*r)
Archimede basò il lavoro di calcolo del π sui poligoni inscritti e
circoscritti. Calcolò il perimetro di un esagono inscritto e poi di uno
circoscritto, ripetendo il processo per poligoni di 12, 24, 48 e 96 lati.
Poligoni regolari di 6 lati
Poligoni regolari di 24 lati
In questo modo capì che il perimetro del poligono, inscritto o
circoscritto che fosse, corrispondeva sempre di più alla misura
della circonferenza con l’aumentare del numero di lati e per
questo l’approssimazione doveva essere più precisa.
Perciò considerò la lunghezza della circonferenza compresa tra i
due perimetri dei poligoni di 96 lati e notò che tale lunghezza era
pari a tre volte il diametro aumentato di una frazione compresa tra
10/71 e 10/70, giungendo alla conclusione che il valore di π era
compreso tra 3+10/71 e 3+10/70.
Poligono regolare
Un poligono è regolare se risulta
contemporaneamente equilatero e equiangolo.
Ogni poligono regolare
ammette una circonferenza
inscritta e una circoscritta.
L'apotema è il raggio della
circonferenza inscritta e
corrisponde alla distanza fissa tra
l'incentro e ciascuno degli n lati.
Poligoni inscritti & circoscritti
Un poligono è inscritto in una circonferenza quando
tutti i suoi vertici appartengono alla circonferenza.
Il centro della circonferenza coincide con il circocentro
del poligono (punto d’incontro degli assi del poligono).
Un poligono è circoscritto in una circonferenza
quando tutti i suoi lati sono tangenti alla
circonferenza.
Il centro della circonferenza coincide con
l’incentro del poligono (punto d’incontro delle
bisettrici degli angoli del poligono).
Numero fisso dei poligoni regolari
In un poligono regolare il rapporto tra l’apotema e il lato è un valore
costante detto numero fisso (f).
𝒇 =𝒂 / 𝒍
a= 0.5*l *cot (p/n)
perimetro :
2p= na/f
Il numero fisso è caratteristico di ogni tipo poligono regolare.
Poligono regolare
Triangolo
Numero fisso
0,289
METODO DI ARCHIMEDE
FIOCCO DI NEVE
Area del pentagono e dell'esagono
AVANTI
CONCLUSIONI
Il nostro laboratorio è stato costruito sulla figura di
Eratostene, grande matematico del passato, non
sempre messo in evidenza. I suoi studi sono stati
rivoluzionari per il suo tempo, basti pensare al calcolo
del meridiano terrestre e alla sfericità della terra.
Inoltre, i numeri primi, il p sembrano, a prima vista,
concetti astratti o troppo lontani da noi; ma la realtà,
quindi la natura, sembra essere scritta con questi
caratteri, si pensi al fiocco di neve visto in precedenza.
GRAZIE PER LA CORTESE
ATTENZIONE
SI RINGRAZIANO GLI STUDENTI E I
PROFESSORI CHE HANNO
CONTRIBUITO ALLA REALIZZAZIONE
DEL PROGETTO.
Grazie a tutti!