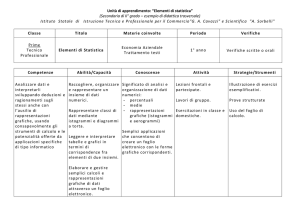
STATISTICA
1
Perché la Statistica
Nei fenomeni collettivi, cioè in quei fenomeni, in
senso generale, in cui gli elementi coinvolti sono
molti, non interessa il comportamento di ogni singolo
elemento, ma interessa il loro comportamento globale.
Esempi: gli alunni di un istituto scolastico; la
popolazione di una nazione; ecc….
2
Una industria deve produrre un prodotto da immettere
sul mercato. Per preparare il prodotto l’industria ha la
necessità di conoscere il gusto della popolazione.
Ovviamente non vengono interpellate tutte le persone
a cui è indirizzato il prodotto per capire quali debbano
essere le sue proprietà, tali da soddisfare il gusto degli
acquirenti.
Si interpellano un gruppo di persone, un campione, si
raccolgono le riposte e si raccolgono i dati, che
vengono opportunamente elaborati matematicamente.
Da questa elaborazione si traggono delle conclusioni,
da cui si ricavano le informazioni molto utili circa il
gusto dei clienti. La fase descritta è un’indagine
statistica.
3
La statistica è la scienza che si occupa della raccolta e
dell'analisi dei dati relativi ad un certo gruppo di
persone, animali o oggetti al fine di descrivere in
maniera sintetica un fenomeno che li riguarda e fare
eventualmente previsioni sul suo andamento futuro.
Statistica deriva da stato, poiché i regnanti
raccoglievano dati demografici ed economici di vitale
interesse per la gestione di una nazione.
Successivamente essa si è sviluppata con metodo
scientifico nell’analisi dei dati ed è applicata in molte
discipline: fisica, chimica, biologia, medicina,
ingegneria, economia, scienze sociali. È diventata una
branca molto importante della matematica.
4
In sintesi: Nelle scienze sperimentali (fisica,
biologia, medicina, ingegneria, scienze sociali)
si progettano esperimenti di vario tipo, si
raccolgono i dati, li si analizzano e si
interpretano i risultati. Per fare questo si usano
argomenti statistici e calcoli matematici.
Quindi la statistica è uno strumento di analisi
dati ed un insieme di metodi e tecniche per:
1.Raccogliere informazioni su un fenomeno;
2.Sintetizzare l’informazione (elaborare dati);
3.Generalizzare i risultati ottenuti.
5
Elementi di un’indagine statistica
La popolazione, da non confondersi con un
gruppo di persone, o universo, è il gruppo di
oggetti che viene preso in considerazione
nell’indagine statistica (esempio: alunni di una
scuola, elettori di una città, le molecole di un
gas, i malati di un ospedale, geni, cellule, ecc..)
6
Elementi di un’indagine statistica
Il censimento è la fase inerente la raccolta di
dati che viene effettuata su di una popolazione.
Il campione è solo una parte della popolazione
che viene presa in considerazione durante
l’indagine statistica. La scelta del campione
viene effettuata in modo che sia una
rappresentanza
significativa
dell’intera
popolazione.
7
Elementi di un’indagine statistica
Fissata una popolazione, si chiamano variabili
statistiche tutte quelle caratteristiche che variano al
variare dei componenti della popolazione.
Esempi:
•il colore bianco, fulvo, nero, ecc..., della pelliccia
degli esemplari di una certa specie,
•il sesso (maschio o femmina),
sono variabili statistiche qualitative (non numeriche),
dette anche attributi.
8
Elementi di un’indagine statistica
Altri esempi di variabili statistiche:
•l'età in mesi dei bambini
•il numero di cuccioli nati da ogni femmina,
sono variabili statistiche quantitative discrete (sono
numeri ben precisi.)
•la temperatura di Roma rilevata alle ore 14 del primo
Giugno di ogni anno
è una variabile quantitativa continua,
In generale le variabili discrete possono assumere
solo un numero finito o una infinita numerabile di
valori, mentre quelle continue possono assumere tutti i
9
valori compresi in un intervallo.
Statistica descrittiva e statistica induttiva
La statistica descrittiva (cioè che
descrive i fenomeni) è l’insieme di
metodi e tecniche per l'esplorazione e la
sintesi
dell'evidenza
empirica
o
sperimentale (dati), ovvero l’insieme di
strumenti matematici utilizzati per
descrivere i dati relativi ad un certo
gruppo scelto come popolazione. Essa si
occupa dell’analisi dei dati osservati.
10
Statistica descrittiva e statistica induttiva
La statistica descrittiva spiega come i
dati raccolti devono essere riportati in
tabella, rappresentati in grafici e
sintetizzati in indici matematici, allo
scopo di individuare le caratteristiche
fondamentali del campione.
11
Statistica descrittiva e statistica induttiva
Lo scopo principale della statistica
descrittiva è di ridurre il volume dei dati
osservati, esprimendo l’informazione
contenuta dei dati per mezzo di tabelle, di
grafici e indicatori numerici che li
descrivono.
Inoltre si possono effettuare indagini di
tipo comparativo e si può verificare
l’adattarsi dei dati sperimentali ad un
certo modello teorico.
12
Statistica descrittiva e statistica induttiva
Lo scopo principale della statistica descrittiva è
di descrivere il fenomeno sulla base dei risultati
contenuti nel campione, senza estendere i risultati
all’intera popolazione e di ridurre il volume dei
dati osservati, esprimendo l’informazione
contenuta dei dati per mezzo di tabelle, di grafici
e indicatori numerici che li descrivono.
Inoltre si possono effettuare indagini di tipo
comparativo e si può verificare l’adattarsi dei dati
sperimentali ad un certo modello teorico.
13
Statistica descrittiva e statistica induttiva
La statistica induttiva (o inferenza – deduzione
statistica) è l’insieme di metodi e principi per dedurre le
caratteristiche generali di un fenomeno mediante
l'osservazione di un insieme limitato di manifestazioni
dello stesso.
Dall’analisi dei dati del campione, mediante adeguati
strumenti matematici si effettuano previsioni circa le
caratteristiche dell’intera popolazione.
È bene precisare che le deduzioni e le previsioni non sono
certezze, ma sono delle asserzioni che vengono formulate
mediante metodi matematici particolari, precisi e
quantitativi, come il calcolo delle probabilità.
14
Statistica descrittiva e statistica induttiva
La statistica induttiva (o inferenza – deduzione
statistica) permette di dedurre leggi generali, disponendo
di un campione di dati variabili. Quindi cerca di estendere i
risultati ottenuti sul campione all’intera popolazione. Per
poter estendere i risultati occorre che il campione sia scelto
con criterio.
15
Fase di un’indagine statistica
Un’indagine statistica per la sua esecuzione richiede di essere
svolta in varie fasi.
Prima fase: Cosa indagare
Prima di tutto è necessario individuare l’oggetto (cosa
indagare) di un’indagine riguardante una certa popolazione.
L’oggetto dell’indagine si chiama carattere. Questi si
distinguono in caratteri qualitativi e in caratteri
quantitativi, che possono essere, a loro volta, discreti e
continui (definizioni visti in precedenza.)
Ogni soggetto o elemento che costituisce una popolazione si
chiama unità statistica.
16
Seconda fase: Come indagare
Il secondo passo consiste come effettuare l’indagine.
Un carattere rappresenta un aspetto di un fenomeno
collettivo che si vuole analizzare. Ciascuno dei possibili
modi in cui un carattere si presenta si chiama modalità.
Esempio: Si vuole analizzare il titolo di studio conseguito
dai giovani. “Titolo di studio” rappresenta il carattere su cui
raccogliere informazioni.
Il titolo di studio può essere la licenza media, diploma di
scuola superiore, laurea. I diversi modi in cui si presenta il
carattere, ovvero il diverso titolo di studio conseguito, si
chiama modalità.
17
Terza fase: Raccolta dei dati
La raccolta dei dati può avvenire o sull’intera popolazione
(chiamata anche insieme universo), allora si dice che si
esegue un censimento (rilevazione diretta o globale), oppure
su una parte della popolazione chiamata campione
(rilevazione indiretta o parziale). Quest’ultimo vien scelta in
modo opportuno in modo da essere una rappresentanza
significativa della popolazione.
L’indagine effettuata sull’intera popolazione risulta più
significativa di quella effettuata su un campione, però risulta
più costosa e più lunga nei tempi. Pertanto l’indagine sul
campione è più redditizia, sia nei costi che nei tempi, però
presenta un certo grado di incertezza nei suoi risultati. Con il
tempo i matematici hanno trovato sistemi per diminuire tali
18
incertezze.
Quarta fase: Spoglio delle schede
La raccolta dei dati avviene mediante la compilazione di
schede o questionari da parte del soggetto “intervistato”.
Una volta eseguita la raccolta delle schede contenenti i dati
dell’indagine, è necessario effettuare lo spoglio per poter
organizzarli. Una buona organizzazione dei dati permette di
trarre informazioni sintetiche sul fenomeno studiato. Pertanto
si inizia il conteggio delle risposte che vengono date a
ciascuna domanda. A tale proposito si predispongono delle
opportune tabelle in cui inserire il conteggio delle diverse
risposte.
19
Quinta fase: Rappresentazione grafica
Per trarre delle informazioni adeguate, i dati, che sono stati
predisposti in tabelle, vengono rappresentati mediante
opportuni grafici. Dallo studio dei grafici e adoperando
adeguati strumenti matematici si traggono informazioni circa
l’indagine statistica.
I grafici possono essere del tipo:
1. Ortogramma
2. Istogramma
3. Aerogramma
20
Tipi di grafici
I grafici possono essere del tipo:
1. Ortogramma
2. Istogramma
3. Aerogramma
4. Diagrammi cartesiani
5. Ideogrammi e cartogrammi
6. Diagrammi a strisce o a colonne
7. Diagrammi circolari o a torta
21
Sesta fase: Elaborazione dei dati
Dai dati sistemati in tabelle e dai grafici che si producono, gli
statistici, adoperando opportune tecniche matematiche,
elaborano i dati.
Dalla interpretazione dei dati si traggono opportune
informazioni.
Se l’indagine è stata
effettuata su un campione, le
conclusioni possono essere considerate valide per l’intera
popolazione.
22
Esempio di indagine statistica
Come esempio di indagine statistica, si possono considerare i
voti conseguiti da una classe al termine dell’anno scolastico.
Poiché l’analisi della classe viene fatta considerando i voti
presi da tutti gli alunni della classe, la raccolta dei dati viene
fatta su una intera popolazione (la classe.)
I dati stati inseriti in un foglio di calcolo Excel.
L’analisi dei dati ed i grafici saranno esguiti utilizzando le
funzioni presenti nel foglio di Excel.
23
24
Analisi dei dati
Alunni della classe
Il numero, N, degli alunni di cui è composta la classe è:
N = 31
Prima di tutto si vuol conoscere come è composta la classe,
cioè conoscere il numero di ragazzi e ragazze. Dal conteggio
risulta:
Ragazzi
Ragazze
9
22
25
Conta-se() – Conteggio condizionato
La funzione di Excel che permette il conteggio dei ragazzi e
delle ragazze è:
conta.se()
Per contare il numero dei ragazzi si deve digitare, in una
qualsiasi cella del foglio, la seguente istruzione:
=CONTA.SE(C2:C22;”M”)
Il significato della scrittura è il seguente:
Conta tutte le “M” (condizione) che si trovano nelle celle
comprese tra C2 e C22.
26
Aerogramma o diagramma a torta
L’ aerogramma, detto anche diagramma circolare o
diagramma a torta, è un utili mezzo per rappresentare le
percentuali di ripartizioni della popolazione rispetto ad una
caratteristica.
Il diagramma viene eseguito utilizzando “Creazione guidata
grafico” di Excel.
27
Aerogramma o diagramma a torta
Il diagramma a
torta ha il pregio di
fornire
subito
visivamente l’idea
di
come
sono
suddivisi, in ragazzi
e ragazze, gli alunni
della classe.
I numeri che vi compaiono indicano: il primo numero indica il
valore assoluto di ragazzi e ragazze; il secondo la percentuale.
L’ampiezza degli angoli dei settori circolari sono in relazione
alla percentuale.
28
Percentuale - Calcolo
La percentuale, che indica la suddivisione tra ragazzi e
ragazze della classe, si calcola nel seguente modo:
Siano
N = 31;
Ragazzi = 9;
Ragazze = 22
Rispettivamente, il numero totale degli alunni, il numero di
ragazze e di ragazze. Il calcolo della percentuale dei ragazzi
presenti nella classe è il seguente:
31
: 100
9 :
Totalità Intero
Ragazzi
x
da cui si ha:
Percentual e
9 100
x
29,03%
31
29
Media aritmetica
Volendo confrontare il rendimento scolastico dei singoli
alunni, è molto comodo avere a disposizione un solo numero
piuttosto che tutti i voti, da cui non sarebbe possibile ricavare
una informazione immediata.
Il numero capace di sintetizzare il rendimento scolastico è la
media aritmetica.
Definizione: La media aritmetica di una distribuzione
statistica di dati numerici è il rapporto tra la somma di tutti i
dati raccolti ed il loro numero.
30
Media aritmetica
Applicazione della definizione al calcolo della media
aritmetica dei voti del primo alunno della tabella: “Agata”
Si indicano con
n = 10
il numero di discipline (numero di dati) e con
x1, x2, x3, x4, ……., xn
i voti delle singole discipline (dati raccolti).
31
Media aritmetica
La media aritmetica, M, si calcola nel seguente modo:
x1 x 2 x 3 x 4 ..... x n
M
n
oppure, in modo sintetico,
n
M
x
i 1
n
i
Si legge: Sommatoria di xi, con i che varia da
1 ad n.
Il simbolo Σ, sigma lettera greca maiuscola,
viene utilizzato in matematica per indicare
una somma di molti termini.
32
Media aritmetica
Sostituendo nella formula i numeri che indicano i voti, si
calcola la media dell’alunna “Agata”.
8888877978
M
7,80
10
Questa operazione deve essere eseguita per tutti gli altri
alunni.
33
Media aritmetica interra classe
8888877978
M
7,80
10
34
Media aritmetica con Excel
Con Excel la media aritmetica si calcola nel seguente modo:
1.Posizionamento del cursore nella cella
nella diapositiva precedente);
2.Digitare:
N2 (vedere figura
=SOMMA(D2:M2)/10
Con Excel, quando in una cella si immette una qualsiasi
formula matematica, la formula viene sempre preceduta dal
simbolo di uguaglianza (=).
Il significato della formula è il seguente:
Sommare tutti i numeri compresi tra le celle D2 e M2
[SOMMA(D2:M2)], e dividere (/) per 10, dove 10 è il
numero delle discipline.
35
Media aritmetica con Excel
Per calcolare le medie aritmetiche degli altri alunni
bisognerebbe riscrivere la precedente formula.
Con Excel questo procedimento può essere evitato seguendo
la seguente procedura:
1.Si posiziona il cursore sulla casella N2.
2.Si posiziona il cursore nella parte bassa a destra della
casella;
3.Compare un piccola “croce”;
4.Tenendo premuto il tasto sinistro del mouse, si trascina in
verticale il contenuto della cella N2. I numeri che compaiono
sono le medie aritmetiche di tutti gli alunni.
36
Media aritmetica ponderata
Osservando i voti di “Agata” si nota che alcuni voti si
ripetono diverse volte.
Il voto “7” compare “3” volte;
Il voto “8” compare “6” volte;
Il voto “9” compare “1” volte;
I voti “7”, “8” e “9” rappresentano le modalità.
I numeri “3”, “6” e “1”, rispettivamente, rappresentano quante
volte si presentano i voti “7”, “8” e “9”. Questi numeri si
chiamano “frequenza” o, nel calcolo della media, “peso”.
37
Media aritmetica ponderata
Pertanto, invece di calcolare la media come fatto in
precedenza, che non è conveniente quando si hanno molti
numeri,
8888877978
M
7,80
10
si utilizza il concetto di peso e, quindi, di media pesata.
Indicando con x1, x2, x3, …., xi i voti, e con p1, p2, p3, …., pi i
rispettivi pesi, o frequenze, la media ponderata risulta:
n
x p
i
i
x1 p1 x 2 p 2 x 3 p 3 x 4 p 4 ..... xn p n
i 1
M
p1 p 2 p 3 p 4 .... p n
p1 p 2 .. p n
38
Media aritmetica ponderata
Elaborando ulteriormente
ponderata, si ottiene:
l’espressione
n
M
x p
i 1
i
della
n
i
p1 p 2 .. p n
media
n
x p x p
i
i 1
i
n
p
i 1
i 1
i
i
n
i
Nel caso dell’alunna “Agata”, la media ponderata risulta:
7 3 8 6 9 1 21 48 9 78
M
7,80
3 61
10
10
39
Media aritmetica ponderata
Ulteriore applicazione della media aritmetica ponderata a tutta
la classe.
Nella tabella-figura sono indicati i voti ed i corrispondenti
pesi.
Il peso totale vale 310. questo
numero deriva dalla seguente
moltiplicazione
1031=310
Dove: 10 = numero di discipline
31= numero di alunni.
40
Media aritmetica ponderata
La media aritmetica ponderata della intera classe risulta:
6 62 7 89 8 87 9 66 10 6
M
62 89 87 66 6
372 623 696 594 60 2345
M
7,56
310
310
Sempre con Excel, la media aritmetica dell’intera classe si
ottiene digitando il seguente comando:
=SOMMA(D2:M32)/310
Il cui significato è: sommare tutti i numeri compresi nel
rettangolo i cui vertici estremi sono le celle D2 e M32, il tutto
41
diviso per 310 (Numero di discipline numero alunni).
Media aritmetica con Excel
Con Excel la media aritmetica si calcola con la seguente
formula predefinita dal software:
=MEDIA(D2:M32)
Il significato è della formula: Effettuare la media dei numeri
compresi in un rettangolo di celle comprese tra D2 e M32.
42
Frequenza
Per definire il concetto di frequenza, si riconsidera la
seguente figura.
Voto è il carattere dell’indagine
statistica.
6, 7, 8, 9 e 10 sono le modalità
con cui si manifestano i caratteri.
62, 89, 87, 66 e 6 sono il numero di volte con cui si presentano
le modalità. Questi numeri si chiamano frequenza (oppure
peso). L’insieme delle modalità e delle loro frequenze si chiama
distribuzione statistica delle frequenze, oppure distribuzione
di frequenze.
43
Frequenza assoluta
Pertanto si ha la seguente definizione di frequenza:
La frequenza assoluta di una modalità è il numero che indica
quante volte il carattere si è manifestato.
La frequenza risulta assoluta perché non tiene conto della
totalità delle modalità.
44
Frequenza o peso con Excel
Con Excel, il peso, o frequenza, relativo al voto “6” si
calcola nel seguente modo:
=CONTA.SE(D2:M32;”6”)
Il comando CONTA.SE è un comando condizionato ed ha il
seguente significato:
Conta quante volte compare il carattere (voto) “6” in tutte le
caselle comprese in un rettangolo (di caselle) i cui vertici
opposti sono le celle D2 e M32.
Nello stesso rettangolo di celle si calcolano i pesi dei restanti
voti.
45
Frequenza relativa
Se la frequenza viene calcolata facendo riferimento alla
totalità delle modalità, si ottiene la frequenza relativa.
Pertanto la frequenza relativa di una particolare modalità è il
rapporto tra la frequenza della modalità ed il numero totale
delle rilevazioni.
Indicando con F la frequenza
assoluta e con T la totalità delle
rilevazioni, allora la frequenza
relativa, f, risulta:
F
f
T
46
Frequenza relativa percentuale
Moltiplicando per 100 la frequenza relativa si ottiene la
frequenza percentuale.
Esempio:
La frequenza relativa
percentuale relativa al
voto 8 è:
87
f8
100 28,06
310
47
Frequenza grafici: Torta
Per
una
lettura
immediata dei dati
presenti nella tabella
si eseguono delle
rappresentazioni
grafiche. Un primo
grafico è quello a
torta, che fornisce le
relazioni percentuali
tra
le
diverse
modalità. La torta è in
settori separati.
48
Frequenza grafici: Torta
Un altro tipo di
grafico a torta è
quello in cui i vari
settori non
sono
separati
49
Frequenza grafici: Ortogramma
Un altro tipo di
grafico
è
l’ortogramma.
In questo tipo di
grafico si mettono a
confronto
le
frequenza assolute.
Le
altezze
dei
rettangoli hanno la
stessa base, mentre
le altezze sono in
proporzione
alle
frequenze assolute.
50
Classi di frequenze
Un ulteriore approfondimento del profitto degli alunni è quello
di studiare la media dei loro voti.
Osservando le medie, si constata che esse sono diverse tra di
loro; allora le medie, ovvero le modalità, vengono raggruppate
in classi. Per ognuna di queste classi viene determinata la
frequenza sia assoluta che relativa.
51
Classi di frequenza
Media dei voti, M: oggetto
da studiare, modalità.
6,5 < M 6,5 : Esempio di
raggruppamento della
modalità in classi.
Frequenza: Frequenza assoluta in cui si presenta una certa classe.
Frequenza relativa percentuale: Frequenza relativa alla totalità.
Classe: Suddivisione delle medie dei voti in intervalli prestabiliti,
esempio [6,5 – 7]. Per ogni classe il valore più piccolo viene escluso.
Esempio: il valore 6,5 appartiene alla classe [6 – 6,5] e non alla classe
[6,5 - 7].
52
Classi di frequenza: Istogramma
Per rappresentare
i dati che sono
stati suddivisi in
classi, i utilizza
l’Istogramma.
L’Istogramma è
composto da
rettangoli la cui
area è
proporzionale
alla frequenza. Se
le basi sono tutte
uguali, l’altezza
dei rettangoli
coincidono con le
frequenze.
53
Indice di posizione centrale
La media della classe è M=7,56. la
media indica un valore di sintesi, cioè è
un valore che riassume una caratteristica
di un insieme dei dati (in questo caso la
media dei voti di fine anno scolastico.)
Questo valore si trova molto vicino alla
zona in cui si addensano di più le medie
dei voti (Intervallo di medie: 7-7,5;
frequenza=7).
Quando la media totale, o valore di
sintesi, si trova nella zona in cui si
addensano i risultati, si chiama indice di
posizione centrale. Non sempre la
media è un buon indice centrale.
54
Mediana
Si considerino i valori ottenuti durante un’indagine:
3, 12,
5,
8,
15,
2,
63
La media aritmetica della serie di valori è:
3 12 5 8 15 2 63 108
M
15,4
7
7
Il valore della media è più grande di tutti i numeri, ad eccezione
del valore 63. Questo significa che la media calcolata non è un
buon indice di posizione centrale, poiché sposta in avanti il valore
medio rispetto alla posizione centrale.
55
Mediana
Per trovare un buon indice di posizione centrale, si eseguono le
seguenti operazioni:
• si ordinano in senso crescente i numeri della serie di valori:
2;
3; 5; 8;
12; 15; 63
•Si scegli il numero centrale della serie di valori, che corrisponde
al numero 8. Questo numero prende il nome di Mediana. È da
notare che il numero di valori è dispari (i valori sono 7.)
56
Mediana
Se il numero di valori della serie di dati è pari, allora, dopo averli
ordinati, si prendono i due valori centrali e si esegue la loro media
aritmetica. Tale valore è la mediana cercata.
Esempio: i dati sono:
12, 3, 23, 17, 32, 15, 45, 27, 52, 31
La serie di dati ordinata è:
3, 12, 15, 17, 23, 27, 31, 32, 45, 52
Il numero di valori è 10, che è un numero pari. I due valori centrali
sono il quinto ed il sesto, cioè 23 e 27.
La media dei due valori è:
23 27 50
M
25
2
2
Pertanto la mediana vale 25.
57
Mediana
Definizione di Mediana:
Data una sequenza ordinata di N numeri x1, x2, x3, …., xN, la mediana
è:
•Il valore che occupa la posizione centrale, se N è dispari;
•La media aritmetica dei due valori centrali, se N è dispari.
58
Moda o valore modale
Si prendono in considerazione i voti conseguiti dagli alunni in
Latino.
Si posizionano in senso orizzontale i
voti conseguito in latino:
6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7,
7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9,
10
Osservando i dati riportati, si nota che il voto 6 si ripete con una
frequenza, 11, superiore a tutti gli altri voti. Allora come di indice di
posizione centrale si preferisce assumere il numero 6. Tale numero
prende il nome di moda.
59
Moda
Definizione: Siano dati i numeri x1, x2, x3, x4, ……, xN, si chiama
moda il valore a cui corrisponde la frequenza massima.
Se si considerano tutti i voti conseguiti dalla
classe, si nota che il 7 è il voto cha una
maggiore frequenza. Il numero 7 è la moda
della serie di numeri, che coincidono con tutti
i voti.
Con Excel la moda si calcola utilizzando il seguente comando:
=MODA(D2:M32)
Significato: Calcola la MODA dei numeri compresi nella matrice
rettangolare i cui vertici estremi, ovvero il primo numero e
60
l’ultimo numero, sono D2 e M32
Moda
Se nella distribuzione dei dati vi sono più numeri che
hanno la stessa frequenza massima, allora la moda si
dice bimodale, se vi sono due massimi, o plurimodale,
se vi sono più di due massimi
Se la distribuzione
dei
numeri
è
suddivisa in classi,
come la media dei
voti, allora si parla di
classe modale.
61
Indici di variabilità o di dispersione
Non sempre la media e gli indici di posizione centrale
sono indicativi dell’andamento di una serie di dati. Cioè
non indicano sufficientemente come si distribuiscono
tali valori intorno al valore centrale.
Il significato di quanto detto lo si può vedere facendo
un esempio.
62
Indici di variabilità o di dispersione
Si consideri la seguente serie di dati:
Entrambe le serie di
dati hanno la stessa
media: M = 18.
Come si può
osservare, la
distribuzione dei
valori delle due serie
intorno alla media è
diversa.
63
Indici di variabilità o di dispersione
Un primo modo di indicare la differenza tra le due serie
è quello di introdurre seguente definizione:
Definizione: Si definisce campo
di variazione ( o range) di una
variabile statistica la differenza
tra il suo valore massimo ed il
suo valore minimo.
Nella prima serie il range è di 9
(24-15=9).
Nella seconda serie il range è
37 (40-3=37)
64
Indici di variabilità o di dispersione
Le due serie di dati pur avendo la stessa media hanno
campi di variazioni molto diversi tra di loro. Questo
significa che l’informazione che si trae è approssimata.
Inoltre non rivela sufficientemente come sono distribuiti
i dati all’interno della distribuzione.
In statistica per misurare la variabilità o la dispersione
dei dati delle due serie si utilizzano degli indici di
variabilità. Questi permettono di misurare di quanto
variano i dati da analizzare rispetto al centro della
distribuzione, ricavandone ulteriori informazioni.
Un esempio di indice di variabilità è il campo di
65
variazione (o range).
Scarto dalla media
Un altro indice di variabilità o di dispersione è lo scarto
dalla media.
Definizione: Si dice scarto
dalla media di un valore della
distribuzione
statistica
la
differenza il valore stesso e la
media.
Se M è la media e xi uno dei
valori della distribuzione,
allora lo scarto dalla media, si,
è:
si = xi - M
66
Scarto dalla media
Calcolo degli scarti dalla media, sn.
s1 = 15 – 18 = -3
s2 = 19 – 18 = 1
s3 = 24 – 18 = 6
s4 = 14 – 18 = -4
s5 = 17 – 18 = -1
s6 = 16 – 18 = -2
s7 = 21 – 18 = 3
s8 = 18 – 18 = 0
67
Scarto dalla media
Se si addizionano tutti gli scarti:
s1 + s 2 + s3 + s4 + s 5 + s 6 + s 7 + s 8 =
= -3 + 1 + 6 – 4 - 1-2 + 3 + 0 = 0
Si nota che la somma è nulla.
Quindi in generale si ha:
La somma degli scarti, si, dalla media, M, di una
variabile statistica è uguale a zero.
n
Somma degli scarti x i M 0
i 1
68
Scarto dalla media
Su di un sistema di
assi cartesiani si
possono
rappresentare sia la
serie di valori si la
media dei valori. In
questo modo si
osservano come si
disperdono i valori
intorno al media. Il
grafico che si
ottiene si chiama
grafico di
dispersione.
69
Scarto dalla media
La seconda serie di
dati ha il seguente
grafico di
dispersione.
70
Scarto dalla media
Confronto tra i grafici di dispersione delle due serie di dati.
Nel primo grafico la dispersione rispetto alla media è meno
accentuata della seconda.
71
Scarto assoluto dalla media
Poiché la media degli scarti è sempre nulla, essa non
fornisce indicazioni accettabili di come variano i dati,
allora si introduce una nuova quantità: lo scarto assoluto
della media.
Pertanto, una volta calcolato lo scarto di un dato della
distribuzione statistica, si calcola il suo valore assoluto.
Se xi indica un dato ed M indica la media della
distribuzione, allora lo scarto assoluto, si, vale.
s i xi M
72
Scarto assoluto dalla media
Gli scarti assoluti della prima serie di dati sono:
s1 15 18 3
s 2 19 18 1
s 3 24 18 6
s 4 14 18 4
s 5 17 18 1
s 6 16 18 2
s 7 21 18 3
s 8 18 18 0
73
Scarto semplice medio
Degli scarti assoluti si fa una media. Il valore che si
ottiene è lo scarto medio.
Definizione: Lo scarto medio semplice, S, di una
sequenza di numeri x1, x2, x3, …, xn è la media
aritmetica degli scarti assoluti dei numeri stessi dalla
loro media aritmetica.
n
xi M
i 1
n
S
74
Scarto semplice medio
Applicando la definizione all’esempio precedente si
ha:
s1 s 2 s 3 s 4 s 5 s 6 s 7 s 8
S
8
31 6 41 2 3 0
S
2,5
8
75
Scarto semplice medio
Qual è il significato di scarto semplice medio?
Cosa significa che lo scarto semplice medio, S, vale 2,5?
Risposta: Il valore S=2,5 indica che, in media, i valori
della sequenza dei dati si discostano di 2,5 dalla media
aritmetica.
Ciò che interessa è lo scostamento di un dato dalla media
e non se il dato è maggiore o minore del valore medio
dei dati.
76
Scarto semplice medio
Con Excel il calcolo dello scarto medio si esegue
utilizzando la seguente funzione matematica:
n
xi M
i 1
n
S
MEDIA.DEV (M4 : M11) 2,5
Il significato è il seguente:
Calcola la media delle deviazioni assolute dei loro
valori rispetto alla media. L’intervallo dei dati è
compreso nella matrice i cui vertici opposti di un
rettangolo possono essere, ad esempio, M4 e M11.
77
Varianza
Un altro indice che si utilizza nell’analisi dei dati è la
deviazione standard. Per poterla definire si parte dal
concetto di varianza, che si indica con s2.
Definizione: Data una sequenza di numeri x1, x2, x3, …,
xn di una distribuzione statistica, si chiama varianza, s2,
la media aritmetica dei quadrati degli scarti assoluti dei
dati. Ogni termine |xi - M|2 si chiama scarto
quadratico.
x1 M x 2 M x 3 M .... xn M
2
s
2
2
2
n
2
n
i 1
xi M
n
78
2
Varianza
Un altro modo di calcolare la varianza è il seguente:
n
n
2
xi
2
s
M2
i 1 n
x
i 1
n
2
i
M2
79
Varianza
Con Excel la somma dei quadrati delle deviazioni
dalla media si calcola con la seguente funzione
statistica:
n
s x i M DEV.Q(M 4.M11) 76
2
2
i 1
Con Excel la varianza dell’intera popolazione si
calcola utilizzando la seguente funzione matematica:
n
s
2
i 1
xi M
n
2
VAR .POP (M4.M11) 9,5
80
Deviazione standard
Scarto quadratico medio
Definizione: Si chiama deviazione standard, oppure
scarto quadratico medio, la radice quadrata della
varianza.
x1 M x 2 M x 3 M .... xn M
2
s
2
2
2
n
s
n
i 1
xi M
2
n
81
Deviazione standard
Scarto quadratico medio
Applicazione di varianza e deviazione standard o scarto
quadratico medio alla precedente distribuzione di dati.
La varianza vale:
3 1 6 4 1 2 3 0
76
s
9,5
8
8
2
2
2
2
2
2
2
2
2
La deviazione standard o scarto quadratico medio è:
32 12 62 42 12 22 32 02
s
9,5 3,08
8
82
Deviazione standard
Scarto quadratico medio
Con Excel la deviazione standard, o scarto quadratico
medio, dell’intera popolazione si calcola applicando la
seguente funzione statistica:
s
n
i 1
xi M
n
2
DEV.POP (M4 : M11) 3,8
83
Curva gaussiana
Nella tabella sono riportati le
medie dei voti, suddivise in
classi, da un insieme di classi di
alunni.
Nella prima colonna sono
riportati gli intervalli in cui sono
state suddivise le medie degli
alunni. Nella seconda colonna
sono riportate le frequenze delle
medie che cadono nell’intervallo
indicato.
84
Curva gaussiana
Si riporta su di un istogramma le frequenze dei voti in
funzione degli intervalli in cui sono state suddivise le
medie ottenute dagli alunni al termine di un anno
scolastico.
85
Curva gaussiana
86
Curva gaussiana
Si collegano i punti medi delle basi superiori dei
rettangoli. Si ottiene una spezzata, che avrebbe una
forma a “campana” se la suddivisione in intervalli della
distribuzione dei dati fosse in un grande numero.
La curva teorica che descrive la campana si chiama
gaussiana o curva di Gauss.
Karl Friedrich Gauss (1777-1855) è stato uno dei più
grandi matematici di sempre.
87
Curva gaussiana
Il grafico
riporta una
tipica gaussiana
teorica. La
curva risulta
simmetrica
rispetto al
valore medio,
M, della
distribuzione
dei dati.
88
Curva gaussiana
Il grafico
riporta diverse
gaussiane
simmetriche
tutte rispetto
allo stesso
valore medio,
M.
La diversità delle gaussiane consiste nei diversi valori delle
deviazioni standard o scarto quadratico medio, s.
89
Curva gaussiana
Dal grafico si nota
che se la deviazione
standard è piccola,
la curva è stretta ed
allungata. Ciò
significa che i dati
si addensano
attorno al valore
medio, o valore
aspettato, M, della
distribuzione.
Per valori grandi della deviazione standard, la curva si abbassa e si
allarga. Ciò significa che i dati si addensano di meno rispetto al
valore medio. Ovvero i dati si disperdono di più e si allontanano dal
90
valore medio.
Curva gaussiana
I punti A e C hanno la stessa
ascissa, che vale:
A=C=M–s
I punti B e D hanno la stessa
ascissa, vale:
B=D=M+s
La fascia colorata sotto la curva
gaussiana che ha per estremi i
punti C e D sta a significare che
il 68% dei dati della
popolazione indagata si
distribuisce tra M-s e M+s.
91
Curva gaussiana
Se le ascisse dei punti C e D
sono:
A = C = M –2s
B = D = M + 2s
allora la fascia colorata sotto la
curva gaussiana che ha per
estremi i punti C e D indica che
il 95% dei dati della
popolazione indagata si
distribuisce tra M-2s e M+2s.
92
Curva gaussiana
Se le ascisse dei punti C e D
sono:
A = C = M –3s
B = D = M + 3s
allora la fascia colorata sotto la
curva gaussiana che ha per
estremi i punti C e D indica che
il 99% dei dati della
popolazione indagata si
distribuisce tra M-3s e M+3s.
Dal grafico si nota che quasi la
totalità dei dati di una
popolazione si trova tra M-3s e
93
M+3s.
Curva gaussiana
Confronto tra due gaussiane con valori diversi di deviazione standard.
La prima ha una deviazione standard piccola, con forma stretta e
allungata, la seconda con valore più grande, forma schiacciata e
94
allargata.
Altre medie:
Geometrica - Quadratica - Armonica
Siano x1, x2, x3, ….., xn una serie di numeri positivi. Si
definisce media geometrica, MG, la radice n-esima del
prodotto di tutti i numeri:
MG n x1 x 2 x 3 ..... xn
95
Media Geometrica
Se i numeri x1, x2, x3, ….., xn si ripetono diverse volte, ad
ognuno di essi viene associato una frequenza o peso, f.
Numero
frequenza
x1
f1
xn
fn
La media geometrica ponderata risulta:
MG
n
x1 x2 x3
f1
f2
f3
... xn
fn
96
Media Geometrica
Esempio: Si abbia la seguente serie di numeri:
2, 5, 7, 12, 13, 17
In totale i numeri sono 6.
La media geometrica è:
MG 6 2 5 7 12 13 17 7,55
Comando Excel:
=MEDIA.GEOMETRICA(A1:A6)
97
Media quadratica semplice
Siano x1, x2, x3, ….., xn una serie di numeri positivi. Si
definisce media quadratica semplice, MQ, la radice
quadrata della media aritmetica dei quadrati dei dati.
x1 x 2 x 3 ... x n
MQ
n
2
2
2
2
98
Media quadratica semplice
Esempio: Si abbia la seguente serie di numeri:
2, 5, 7, 12, 13, 17
In totale i numeri sono 6.
La media quadratica semplice è:
22 52 7 2 122 132 17 2
MQ
10,64
6
99
Media quadratica semplice
Se i numeri x1, x2, x3, ….., xn si ripetono diverse volte, ad
ognuno di essi viene associato una frequenza o peso, f.
Numero
frequenza
x1
f1
xn
fn
La media quadratica semplice risulta:
x1 f1 x 2 f 2 x 3 f 3 ... x n fn
MQ
f1 f 2 f 3 ... f 4
2
2
2
2
100
Media armonica semplice
Siano x1, x2, x3, ….., xn una serie di numeri positivi. Si
definisce media armonica semplice, MA, il reciproco
della media aritmetica dei reciproci dei dati.
1
n
MA
1 1
1
1
1 1
1
1
...
...
x1 x 2 x 3
xn
x1 x 2 x 3
xn
n
101
Media armonica semplice
Esempio: Si abbia la seguente serie di numeri:
2, 5, 7, 12, 13, 17
In totale i numeri sono 6.
La media armonica semplice è:
6
MA
5,23
1 1 1 1
1
1
2 5 7 12 13 17
102
Media armonica semplice
Se i numeri x1, x2, x3, ….., xn si ripetono diverse volte, ad
ognuno di essi viene associato una frequenza o peso, f.
Numero
frequenza
x1
f1
xn
fn
La media armonica semplice risulta:
f1 f 2 f 3 ... f n
MA
f1 f 2 f 3
fn
...
x1 x 2 x 3
xn
103
Rappresentazioni grafiche
Per le distribuzioni di frequenza di dati qualitativi, le
rappresentazioni grafiche più frequenti sono
- i diagrammi a rettangoli distanziati,
- gli ortogrammi,
- gli areogrammi (tra cui i diagrammi circolari),
- i diagrammi a figure (o diagrammi simbolici).
104
Rappresentazioni grafiche
I diagrammi a rettangoli distanziati, detti anche grafici a
colonne, sono formati da rettangoli con basi uguali ed altezze
proporzionali alle intensità (o frequenze) dei vari gruppi
considerati. A differenza degli istogrammi, i rettangoli non
sono tra loro contigui, ma distaccati; di conseguenza, sull’asse
delle ascisse non vengono riportati misure ordinate ma nomi,
etichette o simboli, propri delle classificazioni qualitative.
Con dati qualitativi o nominali, le basi dei rettangoli sono
sempre identiche avendo solo un significato simbolico.
105
Rappresentazioni grafiche
Diagrammi a rettangoli distanziati
106
Rappresentazioni grafiche
Gli ortogrammi o grafici a nastri sono uguali ai rettangoli
distanziati; l’unica differenza è che gli assi sono scambiati, per una
lettura più facile.
107
Rappresentazioni grafiche
Barre orizzontali
108
Rappresentazioni grafiche
Gli areogrammi sono grafici in cui le frequenze o le quantità di una
variabile qualitativa sono rappresentate da superfici di figure piane,
come quadrati, rettangoli o, più frequentemente, cerchi oppure loro
parti. La rappresentazione può essere fatta sia con più figure dello
stesso tipo, aventi superfici proporzionali alle frequenze o quantità,
sia con un'unica figura suddivisa in parti proporzionali.
Nel caso dei diagrammi circolari o a torta, si divide un cerchio in
parti proporzionali alle classi di frequenza.
Gli areogrammi vengono usati soprattutto per rappresentare
frequenze percentuali; hanno il vantaggio di fare capire con
immediatezza che la somma di tutte le classi è uguale all’unità (1 o
100%); hanno l’inconveniente che evidenziano con estrema difficoltà
le differenze che non sono molto marcate. Per differenze piccole, si
109
dimostrano meno efficaci degli ortogrammi.
Rappresentazioni grafiche
Aerogrammi o digrammi circolari
110
Rappresentazioni grafiche
Con i diagrammi a figure, detti anche diagrammi simbolici o
pittogrammi, la frequenza di ogni carattere qualitativo viene
rappresentata da una figura, sovente stilizzata, oppure da simboli
che ricordano facilmente l'oggetto. E’ una specie di istogramma
costruito con figure, dove l’altezza della figura deve essere
proporzionale alla frequenza, quando le basi sono uguali.
Questi diagrammi a figure hanno tuttavia il grave inconveniente di
prestarsi a trarre in inganno con facilità il lettore inesperto di
statistica, quando sono stati costruiti con malizia; è pure facile che
un ricercatore non sufficientemente esperto li costruisca in modo
sbagliato, generando non volutamente il sospetto che egli abbia
voluto fornire una impressione di differenza tra i gruppi a
confronto non supportata dai dati.
111
Rappresentazioni grafiche
Diagrammi a figure
112
Rappresentazioni grafiche
Diagrammi a figure
113
Rappresentazioni grafiche
Il cartogramma evidenzia distribuzioni territoriali mediante carte
geografiche, in cui nelle località interessate sono riportati cerchi
proporzionali alle frequenze. E’ il caso delle città segnate su carte
geografiche con cerchi di dimensioni proporzionali al numero di
abitanti. Questi cerchi spesso sono solo simboli, illustrati nelle
didascalie: per cui un solo cerchio bianco spesso indica una
quantità di base (es.: 1.000 persone), due cerchi concentrici
indicano una quantità maggiore, anche in modo non proporzionale
(es.: 20.000 persone), tre cerchi o un cerchio annerito una quantità
ancora superiore (es.: 100.000 persone) e così via. E’ importante
ricordare che, quando costruiti in modo proporzionale, anche
queste rappresentazioni grafiche sono essenzialmente areogrammi
e quindi possono trarre in inganno se ad essere proporzionale alle
114
frequenze è il raggio.
Rappresentazioni grafiche
Per dati quantitativi, riferiti a variabili continue misurate su scale
ad intervalli o di rapporti, di norma si ricorre a istogrammi o
poligoni.
Gli istogrammi sono grafici a barre verticali (per questo detti
anche diagrammi a rettangoli accostati).
115
Rappresentazioni grafiche
Istogrammi
116
Rappresentazioni grafiche
Diagramma cartesiano
117
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
118
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
119
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
120
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
121
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
122
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
123
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
124
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
125
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
126
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
127
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
128
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
129
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
130
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
131
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
132
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
133
Rappresentazioni grafiche
Sequenza di vari tipi di grafici
134
Rappresentazioni grafiche
135
Rappresentazioni grafiche
136
Rappresentazioni grafiche
137
Rappresentazioni grafiche
138
Rappresentazioni grafiche
139
Rappresentazioni grafiche
140
Rappresentazioni grafiche
141
Glossario
• Statistica: è un campo di studio concernente la raccolta,
l’organizzazione, la sintesi e l’analisi dei dati e l’operazione di
inferenza (deduzione) su un corpo di dati, quando soltanto una
parte di essa è osservata.
• Statistica descrittiva: descrive il fenomeno sulla base dei
risultati contenuti nel campione. Non si vuole estendere i risultati
a tutta una popolazione. Pertanto serve a conoscere e
rappresentare in maniera sintetica l’andamento delle variabili in
una popolazione. La statistica descrittiva opera sulla popolazione
o sul campione e consente di organizzare e sintetizzare i dati. Gli
strumenti della statistica descrittiva sono: metodi grafici, misure
di sintesi, indici.
142
Glossario
• Statistica induttiva o inferenziale o deduttiva: cerca di
estendere i risultati ottenuti sul campione all’intera popolazione.
Per poter estendere i risultati occorre che il campione sia scelto
con criterio (casuale). Quindi serve prendere delle decisioni su
un gran numero di dati esaminando soltanto una piccola parte di
essi. La statistica induttiva consente di prevenire, attraverso
l’inferenza statistica, ad una conclusione su una popolazione su
una base dell’informazione contenuta in un campione che è stato
estratto da quella popolazione. Gli strumenti della statistica
inferenziale: stimatori, intervalli di confidenza, verifiche di
ipotesi.
• Probabilità: tecniche connesse al trattamento della casualità e
alla descrizione dei modelli teorici.
143
Glossario
• Fenomeno statistico: l’oggetto della nostra indagine.
•
Unità statistica sono gli elementi o casi componenti il fenomeno
collettivo, che costituiscono l’oggetto diretto dell’osservazione.
• Popolazione (o collettivo statistico) è l’insieme di tutte le unità
statistiche accomunate da una o più caratteristiche, ovvero
l’insieme degli individui portatori della caratteristica di interesse.
• Censimento: Indagine che viene affettuata sull’intera popolazione
• Campione: parte rappresentativa della popolazione, ovvero
sottogruppo o sottoinsieme della popolazione oggetto dello studio
scelto in modo opportuno.
144
Glossario
• Modello: oggetto teorico che descrive le caratteristiche
principali e più importanti del fenomeno.
• Carattere: aspetto, caratteristica, attributo di una unità statistica;
esso coincide con il fenomeno oggetto di studio quando questo è
direttamente osservabile su ciascuna unità.
• Modalità: Ogni diversa presentazione del carattere osservato su
ciascuna unità statistica. Devono essere esaustive rispetto al
carattere e mutuamente esclusive (per ogni unità deve risultare
individuabile una sola modalità.) Esempio: il carattere sesso si
presenta in due modalità: maschile e femminile.
145
Glossario
• Carattere qualitativo: carattere che viene descritto da attributi
(Esempio: sesso, colore, gruppo sanguigno.)
• Carattere quantitativo: carattere che viene descritto da numeri
(Esempio: età, voto, peso.)
• Carattere discreto: è un carattere che può assumere solo valori
specifici o particolari; non ci non vi sono valori intermedi
(Esempio: il numero di auto in un garage è un numero intero e
non decimale.)
• Carattere continuo: carattere che non si limitano ad assumere
solo determinati valori (Esempio: l’altezza di persone non è un
numero fisso o discreto, ma può assumere un valore qualsiasi.)
146
Glossario
• Variabile statistica: caratteristica che assume valori diversi su
diverse persone, luoghi, cose. Le variabili statistiche sono tutte
quelle caratteristiche che variano al vaiare dei componenti dela
popolazione. (Esempio: l’altezza dei ragazzi, il peso di alunni, il
voto in una disciplina.)
• Variabile statistica quantitativa: Sono variabili che possono
essere misurate: (Esempio, età, peso, statura, voto.)
• Variabili statistica qualitative: Sono variabili che non possono
essere misurate, ma possono solo essere divise in categorie, cioè
possono solo essere classificate (esempio: colore dei capelli,
appartenenza ad un gruppo etnico, sesso.)
• Variabile statistica empirica: Sono variabili sperimentali ricavate
in modo diretto attraverso la misurazione dei caratteri del collettivo
statistico o ricavate indirettamente da registri o da altre fonti. 147
Glossario
• Variabili statistiche teoriche: Sono variabili ottenute mediante
elaborazioni matematiche (Esempio: la media.)
• Variabile casuale: Variabile i cui valori sono il risultato di
fattori casuali, che non possono essere esattamente predetti
anticipatamente (Esempio: l’altezza di una persona da adulto, in
quanto non si può predire, quando un bambino nasce, quale sia
esattamente la sua statura raggiunta da adulto, che dipende da
numerosi fattori sia genetici che ambientali.)
• Variabile continua: La variabile continua è una variabile che
può assumere un qualsiasi valore.
148
Glossario
• Frequenza, o frequenza assoluta: La frequenza, o frequenza
assoluta, F, è il numero di volte in cui è stata osservata una certa
modalità nel campione studiato.
• Frequenza relativa: la frequenza relativa, f, è il rapporto tra la
frequenza assoluta, F, ed il numero totale, N, delle unità
statistiche, o delle osservazioni osservate di una certa modalità.
f
F
N
• Frequenza percentuale: La frequenza percentuale è la
frequenza relativa rapportata a 100. Si ottiene moltiplicando la
frequenza relativa per 100.
f
F
100
N
149
Glossario
• Frequenza cumulata: La frequenza cumulata è la somma delle
frequenze delle modalità inferiori o uguali ad una data modalità.
È il numero di unità statistiche che hanno più modalità. La
frequenza cumulata offre informazioni importanti quando si
intende stimare il numero totale di osservazioni inferiore (o
superiore) ad un valore prefissato.
150
Glossario
• Classe: Suddivisione in intervalli dell’insieme dei valori, che
possono assumere le variabili. In generale, la suddivisioni in
classi dell’insieme dei valori avviene quando i valori delle
osservazioni sono numeri decimali (esempio: le altezze delle
persone; la media dei voti conseguiti dagli alunni), oppure
quando il numero di osservazioni è elevato.
• Intervallo: Insieme di valori compresi tra due numeri assegnati
(esempio: l’intervallo [7 – 7,5] è l’insieme di tutte le medie degli
alunni comprese tra i valori 7 e 7,5. tale intervallo si chiama
classe.
• Frequenza di classe: Numero di osservazioni di una variabile
che cadono all’interno di una classe.
151
Glossario
• Valore centrale della classe: Punto o valore medio tra gli
estremi di una classe, che si ottiene dividendo per due la somma
degli estremi dell’intervallo di una classe. Il valore medio della
classe [7 - 7,5] è:
7 7,5
Valore centrale
7,25
2
• Serie statistiche: Tabelle che nella prima colonna riportano le
modalità di un carattere qualitativo.
• Seriazioni statistiche: Tabelle che nella prima colonna riportano
un carattere quantitativo.
152
Glossario
• Medie di calcolo: Sono medie che si calcolano tenendo conto di
tutti i valori della distribuzione (media aritmetica, media
ponderata, media geometrica, media armonica, media
quadratica).
• Medie di posizione: Sono medie che calcolano tenedo conto
solo di alcuni valori (mediana, moda).
• Media aritmetica: Dati n numeri x1, x2, x3, …, xn, la media
aritmetica, M, è il quoziente tra la somma di tutti i numeri ed il
numero n.
n
x x 2 x 3 ..... xn
M 1
n
x
i 1
i
n
153
Glossario
• Media aritmetica ponderata: Dati i numeri x1, x2, x3, …, xn, e
le relative frequenze o pesi F1, F2, F3, …, Fn, si chiama media
aritmetica ponderata, P, è il quoziente tra la somma dei prodotti
tra i numeri e le frequenze e la somma della frequenze.
n
x i Fi
x1 F1 x 2 F2 x 3 F3 ..... xn Fn
i 1
M
F1 F2 F3 .... Fn
F1 F2 ... Fn
• Mediana:
154
Bibliografia
Testi scolastici consultati:
•Bergamini-Trifone-Barozzi: Matematica.verde vol. 1
•Acquaviva-Cornelli-Puppo: Matematica Vol. 2
•Re Franceschini-Grazzi: Moduli.mat – Statistica e
probabilità tomoD
•Andreini-Manara-Prestipino-Saporiti: Pensare e fare
matematica, Algebra 1
•Silvestri: Statistica medica – 01 statistica (file internet)
155
Bibliografia
Testi scolastici consultati:
•Silvestri: Statistica medica – 02 statistica (file internet)
156