momento magnetico indotto

Lezione 8: proprietà magnetiche della materia,
Fenomeni magnetici
Tutti i materiali godono di proprietà magnetiche:
materiali ferromagnetici: fortemente attratti da magneti
materiali non ferromagnetici: debolmente respinti
debolmente attratti
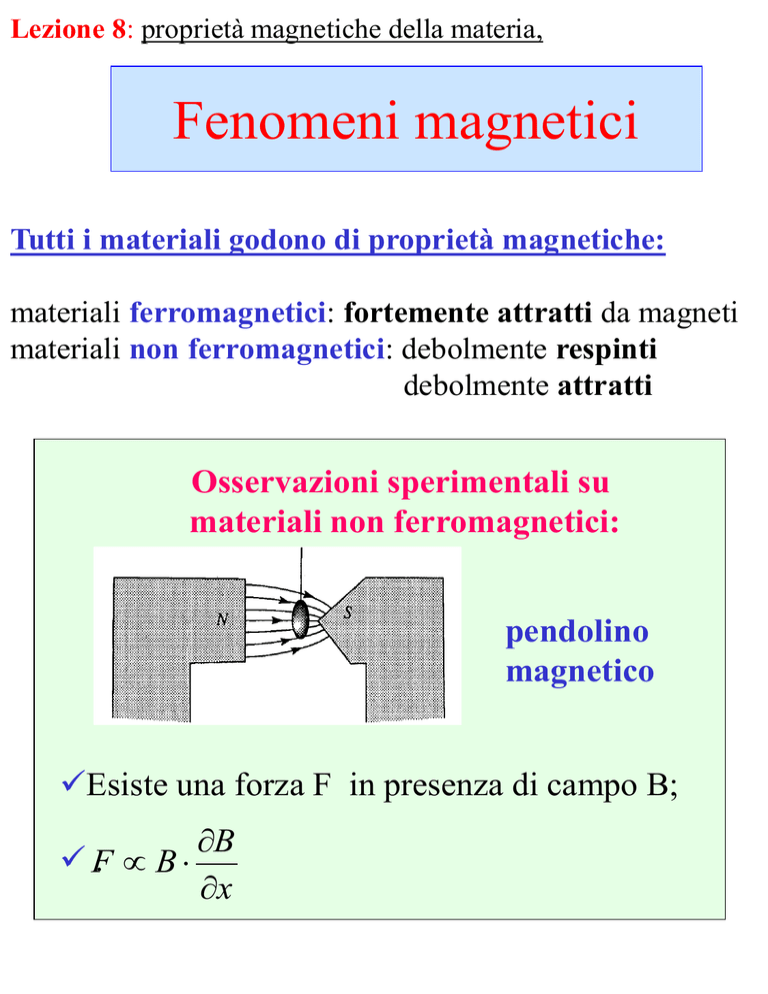
Osservazioni sperimentali su
materiali non ferromagnetici:
pendolino
magnetico
Esiste una forza F in presenza di campo B;
F
.  B
B
x
I motivi di tale fenomenologia sono insiti nella
struttura microscopica della materia
In natura:
 più semplice sorgente di campo magnetico:
dipolo
 spira percorsa da corrente
 ago magnetizzato
le più piccole componenti della materia
(elettroni, protoni, neutroni, quarks e particelle elementari)
hanno un momento magnetico di dipolo non nullo
momento magnetico di dipolo e’ intrinseco alla particella
(non viene da un moto di cariche all’interno della particella)
momento magnetico di atomi e molecole
è dato dalla combinazione di tutti i momenti magnetici delle
sue componenti interne (elettroni,protoni, neutroni ..)
int   i
Paramagnetismo
materiali paramagnetici:
materiali con atomi o molecole
con momento di
dipolo magnetico NON nullo
int   i  0
in assenza di campo magnetico:
momenti magnetici sono
diretti casualmente
effetto globale è quello di un materiale
senza momento magnetico
in presenza di campo magnetico:
 si genera una forza attrattiva (molto debole);
 i dipoli tendono ad allinearsi;
lungo le linee di campo;
il materiale assume momento magnetico non
nullo;
Btot = Bo + BPM
Bo >> BPM
allineamento dei dipoli è contrastato dal moto di
agitazione termica (tende ad orientare casualmente i
momenti magnetici di atomi o molecole)
a temperatura ambiente il moto di agitazione termica
ha il sopravvento sull’allineamento indotto dal campo
magnetico esterno
materiale
paramagnetico:
rapporto B/T
necessario per
allineare una data
percentuale di dipoli
Ascisse:  B/(T*103) Gauss/grado
Ordinate: M/Mmax (percentuale di dipoli allineati)
per esempio:.
A temperatura ambiente
T = 10 Gradi
B = 30*10*103=300000 G = 30 T
per allineare  100 % dei dipoli
materiali paramagnetici:
agitazione termica induce un orientamento
casuale dei dipoli magnetici;
forze magnetiche fra atomi sono troppo deboli
per mantenere allineamento dei dipoli a B esterno.
effetto sfruttato per raffreddare un campione con
smagnetizzazione adiabatica:
campione a contatto termico con serbatoio di
elio liquido (T=1 K);
magnetizzazione del campione, fino alla
saturazione (totale allineamento dei momenti
magnetici - configurazione di minima energia);
isolamento termico del campione e diminuzione
di B:
agitazione termica (ridotta)
disallinea i dipoli aumentando energia
magnetica;
energia termica diminuisce (sistema
isolato!)
si raggiunge T
 10-3 K
Diamagnetismo
proprietà comune a tutti i materiali
diamagnetismo << paramagnetismo
si osserva solo in materiali non paramagnetici
materiali diamagnetici:
materiali con atomi o molecole
con momento di
dipolo magnetico nullo
int   i  0
in presenza di campo magnetico:
 si genera una forza repulsiva (molto debole)
 viene indotto un momento di dipolo che si oppone al
campo magnetico esterno
Btot = Bo - BDM
Bo >> BDM
B0= campo magnetico nel vuoto
Origine del diamagnetismo
Semplice modello di atomo o molecola:
nucleo
positivo
+
due elettroni
su orbita s
in direzione opposta

Btot = 0
campi magnetici
generati dai due elettroni
(spire percorse da corrente)
sono uguali e contrari
in presenza di campo magnetico esterno:
campo magnetico su carica in
moto circolare uniforme aumenta
o riduce la frequenza di rotazione
di una quantità Dw, detta
frequenza di Larmor
qB
Dw 
2m
un elettrone aumenta la frequenza  genera B maggiore
 un elettrone riduce la frequenza  genera B minore

Btot  0
B0= 0: forza elettrostatica tiene legati gli elettroni
Fe = Forza elettrostatica
w0 = velocità angolare
Ftot  qE  mw 02 r
B0 0: i due elettroni risentono della forza di Lorentz:
Fe = Forza elettrostatica
FB = Forza di Lorentz
w = velocità angolare
Ftot  qE  mw o2 r
B0 = 0
Ftot  qE  qvB  mw 2 r
B0  0
qE  qvB  qE  qwrB  mw 2 r
wr  v


qE  mw 02 r
2
2
m
w
r

q
w
rB

m
w
r


0
2
qE  qwrB  mw r 
N.B.
qBw  m w 02  w 2  mw 0  w w 0  w 
si dimostra che:
qBw  m Dw 2w
raggio r costante;
qB
vale anche per
Dw 
frequenza di Larmor
2m
orbite in piani  B0


in presenza di campo esterno B0 0
velocità angolare dell’elettrone varia della quantità
Dw 
qB
2m
detta frequenza di Larmor
momenti magnetici indotti dei due elettroni:
 Dq  2
 w  2 1
2
2
 r  e f  r   e
 r  ewr
2
 Dt 
 2 
1
1 
eB  2
1  ew1r 2  e w 0 
r
2
2 
2m 
  iS  
 
 
1 
eB  2
r
2 
2m 
1
1
 eB 
D  er 2 Dw   er 2 

2
2
 2m 
 
1
2
 2  ew 2 r 2  e w 0 
e 2 Br 2

 3.7 10  29 Am 2
4m
momento magnetico in
più rispetto a quello in
assenza di campo
Legge di Lenz:
il campo aggiuntivo dovuto alla variazione D del moto
orbitale si oppone alla causa che lo ha generato
N.B. momento magnetico indotto da un elettrone in orbita
circolare attorno all’ atomo
1
  ewr 2
2
e2
w
40 mr 3
  9.1 1024 A m 2
mv2
1 e2
Ftot 

r
40 r 2
1
e2
 e
r2
3
2 40 mr
Levitazione magnetica
materiale diamagnetico in presenza di un campo
magnetico esterno sviluppa un controcampo BDM
tanto maggiore è campo esterno Bo, tanto più alta è
l’intensità di BDM (comunque sempre molto inferiore a B0)
in presenza di gradiente di campo magnetico si sviluppa
una forza repulsiva FMag = B.
 Se FMag = mg
il corpo levita nell’aria

FMag  B 
Vol BB
0

FMag 
Vol B 2  mg  Vol g
2 0
2 0 g
B 2 

Esempio:
oggetto piccolo ~10 cm,
solido ( ~1 g/cm3)
diamagnetico (~0.00001)
è sufficiente un campo
B2  1000 T2/m
o che passa da 1 a 10 Tesla
in 10 cm
Ferromagnetismo
materiali ferromagnetici:
materiali di tipo paramagnetico in cui forza creata da effetti quantomeccanici tende ad allineare autonomamente i momenti magnetici di
spin degli elettroni (nonostante il moto di agitazione termica ed
indipendentemente dalla presenza di un campo magnetico o meno).
tale forza esiste solo in 5 metalli (e in alcune loro leghe):
ferro, cobalto, nichel, disprosio e gadolinio
cristallo di materiale ferromagnetico:
elevato numero di elementi (dominii di Weiss)
microscopicamente grandi ma macrospicamente piccoli
(0.1-0.3 mm) al cui interno tutti i dipoli magnetici sono
perfettamente allineati.
assenza di campo: domini allineati a caso
(il materiale non risulta normalmente magnetizzato)
in presenza di campo:
i domini si allineano facilmente:
si genera una forza attrattiva (estremamente intensa)
Btot = Bo + BFM
Bo << BFM
in un materiale ferromagnetico scaldato oltre una certa
temperatura (temperatura di Curie) le proprietà
ferromagnetiche spariscono

il materiale si comporta come paramagnetico
il grado di magnetizzazione di un materiale
ferromagnetico ha una ‘inerzia’:
i domini, dopo essersi allineati in risposta ad un campo
esterno, tendono a permanere in quello stato di allineamento.
Descrizione macroscopica

Vettore Magnetizzazione:
i
 
M i
DV
momento magnetico di dipolo macroscopico
(per unità di volume).
 M quantifica il momento magnetico indotto da un
campo magnetico esterno su un materiale
 M è piccolo per paramagnetici e diamagnetici
grande per ferromagnetici.
Vettore Induzione Magnetica:

  B

H    M 
 0

isola il contributo del campo magnetico generato dai
magneti permanenti o spire percorse da correnti da quello
dei campi magnetici indotti sui materiali;
campi magnetici indotti
sono proporzionali ai campi
magnetici inducenti a meno di
un fattore  (costante di
permeabilità magnetica).



B   0  r H  H


M  (  r  1) H


M  H
 r  1   
 Materiali Diamagnetici
r  1
BDM <<B0
B=B0+BPM
BPM <<B0
B=B0+BFM
BFM >>B0
r < 1
 Materiali Paramagnetici
r  1
B=B0-BDM
r > 1
 Materiali Ferromagnetici
r  r (H) >> 1