Matrici di Rete, parametri S, proprietà strutturali di reti 2, 3 e 4 porte

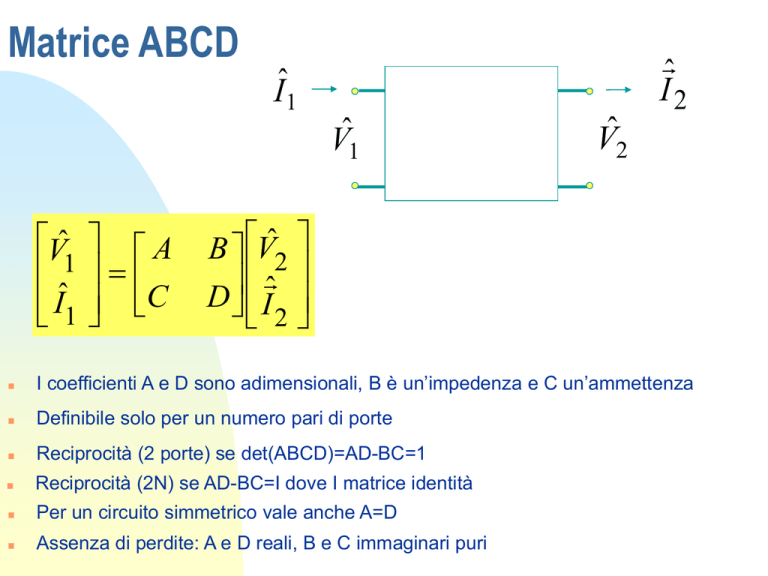
Matrice ABCD
Vˆ
 1
 Iˆ1
 A

 C
Iˆ1
Vˆ1
ˆ
I2
V̂2
B  Vˆ2 
 

D   Iˆ 
 2

I coefficienti A e D sono adimensionali, B è un’impedenza e C un’ammettenza

Definibile solo per un numero pari di porte

Reciprocità (2 porte) se det(ABCD)=AD-BC=1

Reciprocità (2N) se AD-BC=I dove I matrice identità
Per un circuito simmetrico vale anche A=D

Assenza di perdite: A e D reali, B e C immaginari puri

Matrice ABCD Normalizzata
i1  Iˆ1 Z 0
v1  Vˆ1 / Z 0
v   a
 1
 i1  c

b  v2 




d  i 
2
In tal caso tutti i coefficienti sono adimensionali
ˆ

i2  I 2 Z 0
v2  Vˆ2 / Z 0
Matrice di diffusione (S) di un 2 porte


Definiamo quantità legate alle ampiezze delle onde incidenti e riflesse
a1  v 1  V1 / Z 01
b1  v 1  V1 / Z 01
a2  v 2  V 2 / Z 02
b2  v 2  V 2 / Z 02
In tal caso vale (se consideriamo le tensione e le correnti normalizzate alle due porte)
a1  b1  v
a2  b2  v

a1  b1  i
1
2
1

a2  b2  i  i2
2
La matrice S è quella che lega le ampiezze delle onde riflesse a quelle delle onde
incidenti
b   s11
 1
b2  s21
s12  a1 
 

s22  a 
 2
Matrice di diffusione (S) di un 2 porte
a1
b1
s11  b1 / a1 a  0
2
s12  b1 / a2 a  0
1
s21  b2 / a1 a 0
2
s22  b2 / a2 a 0
1




a2
b   s11
 1
b2  s21
s12  a1 
 

s22  a 
 2
b2
Cioè, s11 è legato al coefficiente di riflessione alla porta
1 quando la due è chiusa su carico adattato (non c’è
onda riflessa a2);
Cioè, s21 è legato al coefficiente di trasmissione dalla
porta 1 alla porta 2 quando la due è chiusa su carico
adattato
La matrice S è definita quindi solo quando si
specifichino le impedenze caratteristiche delle linee che
portano l’onda ai terminali dell’oggetto da
caratterizzare, ovvero le impedenze di normalizzazione
La matrice S si definisce perché misurabile anche (e soprattutto) a frequenze di
microonde
Matrice di diffusione (S) di un n porte

definiamo
bT  b1 , b2 ,..,bN 
aT  a1 , a2 ,..,aN 

V
V
i
con b 
ai  i
i
Z 0i
Z 0i

Oppure (il che è lo stesso)

ai   I i  Z 0i
bi  I i - Z 0i




La matrice S è
I cui elementi
b  Sa
Si, j
bi

aj

ak 0 se k  j
Vi  Z 0 j
Vi  Z 0i
Vk   0 se k  j
Notate che, nel caso molto comune di normalizzazione di tutte le porte ad una sola
impedenza caratteristica (tipicamente 50 W) questa diventa

Cioè proprio i coefficienti di riflessione e trasmissione
quando le porte sono chiuse sull’impedenza di
normalizzazione
Si , j 
Vi
Vi 
Vk  0 se k  j
Matrice di diffusione (S) di un n porte

Ma perché usare tale normalizzazione? Se calcoliamo la potenza media che incide
2
alle porte

1 Vi
Pi 
2 Z 0i
1
 ai
2


E la potenza riflessa

1 Vi
Pi 
2 Z 0i




2

1
bi
2
2
Quindi con tale definizione le quantità sono legate all’energia trasportata dal campo
elettromagnetico
La potenza netta entrante nel circuito sarà pari alla differenza tra potenza incidente e
riflessa, sommata su ciascuna porta

1
2
2
1 
a

b
 i

a a  b b
i
2 i
i
2
Ma sappiamo che b  Sa b   a  S 
P   Pi   Pi  

2
quindi
P




1 
1
a a  a  S  Sa  a  I  S  S a
2
2

Matrice di diffusione (S) di un n porte

In assenza di perdite, tale potenza deve essere nulla per qualunque insieme di
eccitazioni a per cui
I  S S  0




S  S  I Condizione di assenza di perdite (Unitarietà di S)
La reciprocità invece implica che S sia simmetrica
ST  S
Consideriamo un due porte simmetrico e senza perdite: vediamo qual è il numero
minimo di parametri necessari a caratterizzarlo; la matrice S è 2x2

Nel definire la matrice S, dobbiamo specificare il piano di
riferimento di fase si ciascuna porta: in pratica dobbiamo per
s
s
 11 12 
esempio specificare in un dispositivo ad una porta, in quale
S

sezione della linea di alimentazione il coefficiente di riflessione
s
s
 12 11 
è misurato. Se la linea è senza perdite, il cambiamento della
sezione comporterà solo un cambiamento della fase del
coefficiente di riflessione
Possiamo quindi sempre scegliere un piano di riferimento per cui la fase di s11 sia
zero, cioè s11 sia reale

S
s12
s12 
 
Proprietà di un 2 porte simmetrico senza perdite

La condizione di assenza di perdite porta a
2
  s12  1
2
S12  S12*  0

 2 Re S12   0
Possiamo porre, parametrizzando
  cos
  arc tan /  
  sin

con

Quindi abbiamo un solo parametro indipendente
2   2 1
S12  j
Proprietà di un 3 porte simmetrico, reciproco, senza perdite


Immaginiamo di avere un 3 porte con simmetria rotazionale, così che s11=s22=s33
Anche in questo caso scegliamo il piano di riferimento per ottenere s11 reale; la
matrice diventa

S   S12
 S12

S12

S12
S12 
S12 
 
Imponendo l’assenza di perdite otteniamo
 
 *
S12
S *
 12
S12*   
* 
S12  S12
  S12

S12*

S12*
 2  2 S12  1


 S12  S12*  S12
2

S12
S12  1 0 0
S12   0 1 0
  0 0 1
1 2
Che NON AMMETTE
 S12 
SOLUZIONI PER =0
2
2
 0 2 Re( S12 )  1    0
2
2
2
S12
Proprietà di un 3 porte simmetrico, reciproco, senza perdite






Quindi un tre porte simmetrico, reciproco e senza perdite non può essere adattato
simultaneamente a tutte le porte
Può esserlo, invece, un 3 porte non reciproco, o uno con perdite
Un particolare 3 porte non reciproco estremamente importante nella pratica è il
circolatore
Di fatti possiamo dimostrare che 3 porte adattato, senza perdite non reciproco è
necessariamente un circolatore
 0 S12 S13 
Infatti la matrice S di un 3 porte adattato è


 S 21 0
 S 31 S 32
Imponendo l’assenza di perdite otteniamo le equazioni
S 31* S 32  0 S 21* S 23  0 S12* S13  0
2
2
S12  S13  1

2
2
S 31  S 32
2
1
Che sono soddisfatte se
S12  S23  S31  0

2
S 21  S 23  1
S 23 
0 
S21  S32  S13  1
Oppure se
S21  S32  S13  0
S12  S23  S31  1

Chiaramente non reciproco
Circolatore


Le due possibili soluzioni corrispondono a due possibili circolatori, uno che consente
flusso di potenza in senso orario e l’altro in senso antiorario
La prima soluzione quindi descrive un circuito che trasmette potenza dalla porta 1 alla
2, o dalla 2 alla 3 o dalla 3 alla 1, ma non in direzione opposta o tra porte non
contigue
 0
 j 2
e
 0

 0

 0
 e j 3


0
0
e j 3
e j1
0
0
e j1 

0 
0 

1
0 
j 2 
e 
0 

1
2
3
Esempio possibile utilizzo: radar in
cui la stessa antenna è usata sia in
trasmissione che in ricezione
2
1
3
2
TX
3
RX
Proprietà di un 4 porte reciproco, senza perdite, adattato alle
S
S 
 0 S
porte


 S12
 S13

 S14

In tal caso la matrice è

Imponiamo l’assenza di perdite
 0
 *
 S12
S *
 13*
 S14
S12*
0
S 23*
S 24*


SS SS
SS SS
S13*
S 23*
0
S 34*
S14*   0

S 24*   S12
S 34*   S13

0   S14
S12
0
S 23
S 24
S13
S 23
0
S 34
12
13
0
S 23
S 24
S 23
0
S 34
S14  1
S 24  0

S 34  0
 
0  0
0
1
0
0
14
S 24 
S 34 

0 
0
0
1
0
0
0
0

1


S 0  0
E sottraendo
S 0   0


*
*
* *
S 24
S
2
2
S13*SS1323S23S
1424S
240  0 E sottraendo
14 S
S14* S13  S 24  0
* * S*  S * S*  0
S
S 14S 13S 24S 23S  0
13
14
13
24
23

*
*
*
*
S

S

S
S
12
12 12
23 23 14 14
34 34
2
S 23 S12  S34
*
*
*
*

S
S
S

14
34 12
14 1234 23
34 23
2
 0
Le due possono essere soddisfatte se S14=S23=0: ACCOPPIATORE DIREZIONALE
I prodotti per gli elementi diagonali danno poi
2
2
2
2
2
2
2
2
S12  S13  1 S12  S 24  1 S13  S34  1 S 24  S34  1
Proprietà di un 4 porte reciproco, senza perdite, adattato alle porte

S13  S24
Che implica
S12  S34
Possiamo scegliere il piano di riferimento in modo che S12 sia reale
S12  S34  
Inoltre, considerando che S13 ed S24 hanno stesso modulo, in forma polare scriviamo
S13  e
j
S 24  e j
Ora valutiamo l’equazione che viene dal moltiplicare riga 2 e colonna 3
S12* S13  S 24* S34  0
Cioè, sostituendo
j
 j  j
 0      
e j  e  j  0  e j  e  j  0  e  e
Due scelte particolari si incontrano nella pratica
   /2
0


 j

0

j
0
0
0
0
j

0
j 


0
Accoppiatore simmetrico o a quadratura di fase,
la cui matrice S è quindi
Notate che, in questo caso, oltre alla simmetria della
matrice imposta dalla reciprocità, essa è simmetrica
anche rispetto alla diagonale secondaria, indicando
un circuito con un piano di simmetria
Proprietà di un 4 porte reciproco, senza perdite, adattato alle porte
  0,  
Accoppiatore antisimmetrico, la cui matrice S è
quindi  0   0 




0
0
0
0
0


  
 

0 
Notate infine che  e  non sono indipendenti, infatti
2
2
S12  S13  1   2   2  1
Ora, analizzando in dettaglio le altre possibili soluzioni, si perviene o a
riconsiderare lo stesso caso sin qui analizzato, o ad ottenere il caso
S12=S13=S24=S34=0, cioè 2 due porte disaccoppiati ed indipendenti


Quindi, escludendo quest’ultimo caso - di nessun interesse- ogni 4-porte reciproco
e senza perdite adattato si comporta come un accoppiatore direzionale.
e l’accoppiatore direzionale in quadratura di fase deve per forza essere simmetrico.
Proprietà di un 4 porte reciproco, senza perdite, adattato alle porte
quindi, schematicamente, un accoppiatore ideale cede potenza alla porta
accoppiata in ragione del fattore di accoppiamento (coupling factor)
2
S13   2
mentre cede tutta la potenza rimanente alla porta diretta
2
S12   2  1   2
La porta rimanente è disaccoppiata o isolata
2
1
1
S12   2  1   2
2
2
S13   2
4
3
isolata
accoppiata
Accoppiatori
Nella pratica caratterizzano un accoppiatore:

Accoppiamento
C  10LogP1 / P3   20Log S13 
Cioè, che frazione della potenza in ingresso è ceduta sulla porta accoppiata

Isolamento
I  10LogP1 / P4   20Log S14 
Cioè, che frazione della potenza in ingresso è ceduta sulla porta isolata

Direttività
D  10LogP3 / P4   20Log S14 / S13 
Cioè, capacità dell’accoppiatore di isolare onde che vanno in una direzione e
direzione opposta
Se la potenza in ingresso si divide tra porta diretta ed accoppiata in parti uguali
(1/2 della potenza va sulla 2 ed 1/2 sulla 3), ovvero se il fattore di accoppiamento è
0 1 j 0 
3dB, si parla di ibridi. In tal caso
    1/ 2



In tal caso, la matrice S per un ibrido ideale a 90° è
mentre, la matrice S per un ibrido ideale a 180° è


1 1 0 0 j 
2  j 0 0 1


0 j 1 0 
0 1 1 0 


1 1 0 0  1
2 1 0 0 1 


0  1 1 0 
Divisore di potenza a “T”
E’ un semplice 3 porte per divisione o combinazione potenza

Essendo reciproco e senza perdite, non può essere adattato a tutte le porte


B è una suscettanza che tiene conto dei
campi dovuti alla discontinuità
Volendo adattare alla porta di ingresso, la
condizione è che
Yin  jB  1 / Z1  1 / Z 2  1 / Z 0


I valori di Z1 e Z2 possono poi essere scelti per avere diversi rapporti di divisione.
Chiaramente le 2 porte rimanenti non possono essere adattate
Trascuriamo inizialmente B, e consideriamo  la frazione trasmessa alla porta 1 ed
1-  quella alla 2; essendo la porta di ingresso adattata otteniamo
Pin 
V02
2Z 0
1
P1  Pin 
1 V0
2 Z1
1
 Z1  Z 0 ; Z 2 
Z0

1
2
1 V0
P2  1   Pin 
2 Z2
2

Chiaramente l’impedenza vista per
esempio guardando nella linea 1,
sarà il parallelo di Z0 e Z2

Chiaramente l’impedenza vista per esempio guardando nella linea 1, sarà
il parallelo di Z0 e Z2
1
Z02
Z0
Z 2 // Z 0  1  

1
Z 0  Z 0 2   
1

Ed il coefficiente di riflessione diviene
Z0
Z
 0
Z 2 // Z 0  Z1 2    
1 

   1
Z
Z
Z 2 // Z 0  Z1
0
 0
2    
Divisore resistivo
Si può adattare alle porte, anche se le porte di uscita non sono isolate

Analizziamo il caso di divisore con fattore 1/2

L’impedenza vista in uno dei rami di
uscita
Z0
4
Z
 Z0  Z0
3
3

Quindi, considerando i due rami di uscita in
parallelo, deve essere
Z in 


Z0 2
 Z0  Z0
3 3
Essendo il 3 porte simmetrico, lo stesso avviene guardando nella porta 2 o
nella porta 3: S11=S22=S33=0
Se la tensione alla porta 1 è V1, la tensione al centro (V) è
2Z 0 / 3
2
V  V1
 V1
2Z 0 / 3  Z 0 / 3
3
V2  V3  V

Z0
3
1
 V  V1
Z0  Z0 / 3 4
2
E le tensioni di uscita


Per cui S21=S31=S23=1/2, ovvero -6dB
Appare chiaro che metà della potenza
è dissipata nei resistori
Divisore Wilkinson
E’ un divisore che utilizza resistori, ma

Se le porte sono adattate, nessuna potenza viene dissipata: solo la potenza
riflessa è dissipata

Consente di ottenere isolamento tra le porte di uscita; studiamo quello a 3dB
Z0
2Z 0
Z0
Z0
2Z 0
/4

Per studiarlo, normalizziamo tutto a Zo
e ridisegniamo evidenziando le
simmetrie
Divisore Wilkinson
Possiamo studiarlo
sfruttando la
sovrapposizione degli effetti

Se volessimo infatti sapere la
risposta del circuito quando
alla porta 2 applichiamo un
generatore Vg2=4V mentre la
porta 3 (Vg3) è lasciata a 0
potremmo prima studiare il caso in cui applichiamo Vg2=Vg3=2V e poi il caso
Vg2=-Vg3=2V: la somma dei due casi produce il risultato desiderato



Calcolare la risposta a tali eccitazioni particolari (simmetrica ed antisimmetrica,
ovvero pari e dispari) è più semplice, poiché la simmetria del problema consente
di ridurre, come vedremo il 2-porte a 2 singole porte indipendenti
Questa è una proprietà del tutto generale dei circuiti con simmetrie, per cui si
possono trovare insiemi di eccitazioni, o autoeccitazioni, che decompongono il
problema a N porte in N problemi ad una porta
Consideriamo i due problemi indipendentemente, a partire dall’eccitazione pari
Divisore Wilkinson
1
Se Vg2 e Vg3 sono uguali,
le tensioni V2 e V3 sono
uguali

2V
1
Quindi non fluisce corrente nel
resistore, che possiamo togliere
2V






Anche nel nodo di ingresso non fluisce corrente: è di fatto un circuito aperto
In pratica c’è uno zero di corrente in tutti i rami che attraversano il piano di
simmetria: si parla di muro magnetico
Il circuito risulta quindi un semplice tratto di linea in quarto d’onda chiuso su
e
resistenza 2, per cui guardano nella porta 2 si vede un’impedenza
Z2
Z in 
2
E chiaramente scegliendo Z pari alla radice di 2, si vede in ingresso 1, cioè
S 22e  0
adattamento; quindi
Ora ci occorrono V1 e V2: sappiamo che l’impedenza che vediamo nel nodo di
e
V2 è 1: quindi abbiamo un partitore resistivo, e V2 risulta V2  V
Per conoscere V1, ricordiamo che si tratta di un tratto di linea
in quarto
d’onda,



j
j
in cui V(0)=V=V++V- V e  V  e  jz  V  e jz  V  e 2  V  e 2   jV  

1
 
  jV   j V  V   j V  2V 

jV 
Divisore Wilkinson
D’altro canto sappiamo anche la corrente che fluisce sul resistore 2









I1e   jV   jV  / Z   jV   jV  / 2   jV  j V  V / 2
  jV / 2




 V1e / 2  j V  2V  / 2  V   1 / 2  1 / 2 V


 V1e  j V  2V    jV 2
Divisore Wilkinson
Trattiamo il caso dispari: Vg2 e
Vg3 sono uguali e opposte

In pratica c’è un massimo di
corrente in tutti i rami che
attraversano il piano di
simmetria, ovvero uno zero di
tensione sul piano di simmetria:
si parla di muro elettrico
2V
-2V

Il circuito risulta quindi quello di partenza in
cui tutti i nodi centrali sono stati rimpiazzati
da un corto a massa


Ora, il corto della porta 1,
dopo un quarto d’onda
diventa un aperto, e
“vediamo” solo r
E vediamo che quindi se
r=2, il coefficiente di
riflessione è nullo, cioè
S 22o  0
Chiaramente ora risulta
V1o  0 V2o  V
Divisore Wilkinson
Per vedere cosa succede alla porta 1, ci comportiamo in modo simile al caso
pari, infatti il circuito appare così
il resistore non è attraversato da corrente (quindi lo possiamo togliere) e si
tratta di due tratti in quarto d’onda, ciascuno
che vede un’impedenza di
2
ingresso normalizzata pari a
2
Z in 
1
2
che posti in parallelo danno di nuovo impedenza 1, cioè adattamento (S11=0)
Ora, per riottenere la matrice S complessiva, bisogna ricombinare i risultati
ottenuti, “pesandoli” con le eccitazioni ipotizzate
in particolare, sappiamo che S22 ed S33 saranno 0, visto che lo sono sia nel
caso pari che nel caso dispari, così come 0 sarà S23=S32, visto che sia nel
caso pari che dispari le porte 2 e 3 sono disaccoppiate
Divisore Wilkinson
grazie al fatto che, in questo caso, tutte le porte sono
adattate se chiuse sull’impedenza di normalizzazione
Per S12 avremmo
S12  S 21 
V1
V2

V1 ,V3 0
V
 1
V2

V1e  V1o
V2  V2
e, per simmetria (porte 2 e 3 interscambiabili)
S13  S12  S31
e
o
 j/ 2